基于Kalman滤波的雷达目标跟踪时间计算方法

夏永红，匡华星，姚　远，丁　春

(中国船舶重工集团公司第七二四研究所，南京 211153)

0　引　言

目标跟踪滤波是主动雷达数据处理中最为重要的环节。Kalman滤波算法具有收敛速度快、存储量小等优点，是目前广泛应用于雷达跟踪系统中的一种自适应滤波算法。[1-2]现有针对Kalman滤波器跟踪性能的研究工作大多关注如何提高其跟踪精度或运算速度，如扩展Kalman滤波算法[3-4]、针对机动目标跟踪改进的Kalman滤波算法等[5-10]，而对于基于Kalman滤波的雷达目标跟踪持续时间分析较少。

本文首先描述实际工程应用中雷达目标航迹维持或终止的物理过程，提出一种目标航迹平均跟踪周期数计算方法，并对两坐标雷达Kalman滤波跟踪性能进行了分析和仿真。仿真结果表明，影响目标航迹平均跟踪周期数的主要因素包括点迹级目标检测概率、虚警概率、雷达测量精度、数据周期以及探测距离。本文的研究成果可为复杂背景下目标跟踪滤波算法流程和参数优化设计提供理论支撑。

1　跟踪持续时间计算

1.1　数学模型假定

主动雷达目标跟踪持续时间取决于关联波门与测量结果的关系，即波门内是否存在真实量测、虚假量测数量或密度、预测位置与波门内所有测量结果的几何关系等。大量仿真研究和试验结果分析表明，在跟踪过程中如果目标回波被成功检测提取，即波门内有真实目标点迹存在，则几乎不会出现航迹跟踪丢失情况。因此，目标航迹持续时间的计算可进行如下物理描述：

(1) 假设在目标跟踪过程中，如该周期有目标检测点迹存在则目标点迹位于关联波门之内。

(2) 如果该周期有目标点迹存在，无论关联波门内是否存在虚假点迹，均认为该周期点航迹能够成功关联，目标航迹延续。

(3) 如果该周期没有检测到目标点迹，且关联波门内也没有虚假点迹存在，则航迹外推，目标航迹延续。对于由于目标点迹级检测概率低、航迹连续多周期未关联更新导致航迹消失的情况本文不予考虑。

(4) 如果该周期没有检测到目标点迹，且关联波门内存在虚假点迹，则目标航迹在该周期终止。

(5) 以上所述的周期是指雷达当前工作模式下设定的数据周期。

1.2　航迹持续时间计算

根据前文所述，目标航迹在当前周期能够延续的条件是关联波门内有目标点迹存在或目标点迹与虚假点迹均不存在，目标航迹终止的条件是当前周期关联波门内没有目标点迹存在且有虚假点迹存在。设目标点迹级检测概率为PD且各周期检测结果相互独立，同时假设关联波门内有虚假点迹存在的概率为Pf且各周期相互独立，则目标航迹持续跟踪周期数概率分布如表1所示。

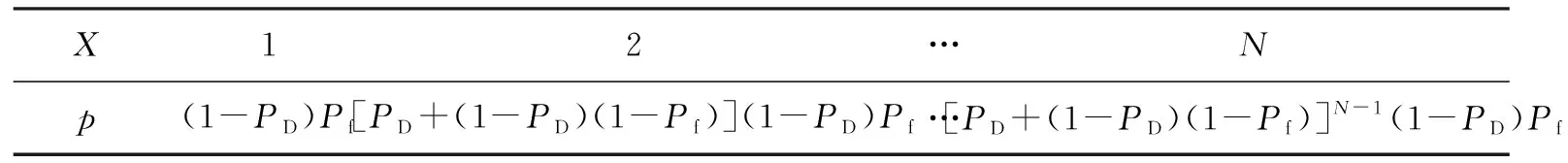
表1　目标航迹跟踪周期数概率分布

表1中，X表示观测周期；p表示航迹在第X周期终止的概率；Pf=1-(1-Pf_plot)Nres≈Nres×Pf_plot(Pf_plot较小时成立)，Pf_plot为点迹级虚警概率，定义为每个检测凝聚分辨单元形成虚假点迹的概率，Nres为关联波门内检测凝聚分辨单元个数(向上取整)。检测凝聚分辨单元是指点迹提取过程中能够满足点迹凝聚准则所要求的最小单元大小，根据雷达分辨力确定。在实际应用中，点迹级虚警概率可以近似为一定区域范围内虚假点迹个数与分辨单元个数之比。

目标航迹平均跟踪周期数为

(1)

目标航迹持续时间定义为

(2)

其中T为当前数据周期。

可以看出，在检测凝聚分辨单元大小、目标点迹级检测概率和虚警概率确定的前提下，目标航迹跟踪周期数仅取决于关联波门的大小，而关联波门则是在Kalman滤波递推迭代过程中动态地计算和调整。

2　Kalman滤波跟踪波门计算

2.1　Kalman滤波算法简介

设系统状态方程为

X(k+1)=F(k)X(k)+Γ(k)v(k)

(3)

式中，X(k)为状态向量；F(k)为状态转移矩阵；Γ(k)为系统过程噪声输入矩阵；v(k)为系统过程噪声，假定为零均值高斯白噪声，其协方差矩阵为Q(k)。

系统量测方程为

Z(k)=H(k)X(k)+W(k)

(4)

式中，Z(k)为量测值；H(k)为量测矩阵；W(k)为量测噪声，也假定为零均值高斯白噪声，其协方差矩阵为R(k)。

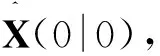
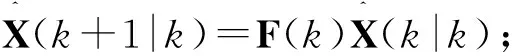
步骤2预测协方差矩阵P(k+1|k)=F(k)P(k|k)FH(k)+Γ(k)Q(k)ΓH(k)；

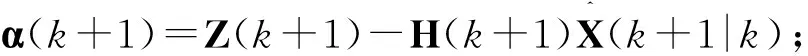
步骤4新息协方差矩阵S(k+1)=H(k+1)P(k+1|k)HH(k+1)+R(k+1)；

步骤5Kalman滤波增益K(k+1)=P(k+1|k)HH(k+1)S-1(k+1)；

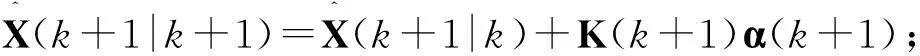
步骤7预测协方差矩阵更新P(k+1|k+1)=[I-K(k+1)H(k+1)]P(k+1|k)。

预测协方差矩阵和新息协方差矩阵均为对称阵。前者用于衡量预测的不确定性，值越小说明预测越精确；后者用于衡量新息的不确定性，值越小说明量测值越精确。

2.2　关联波门大小计算

为了便于跟踪滤波过程中的运动状态外推，目标在空间中的运动状态一般采用直角坐标系进行描述。此时常用的关联波门为矩形波门，当预测误差满足

(5)

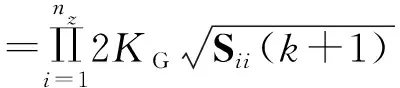
(6)

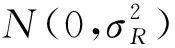
(7)

计算直角坐标系下量测的期望为

(8)

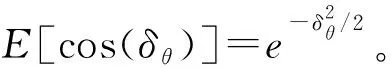
(9)

偏差修正后，其方差和互协方差分别为

(10)

(11)

(12)

对于采用扇形关联波门和圆形关联波门的Kalman滤波算法也可以采用本文方法计算目标航迹跟踪时间。

3　仿真分析

以匀速模型为例，状态向量为X(k)=[x(k)vx(k)y(k)vy(k)]T，观测向量为Z(k)=[zx(k)zy(k)]T，状态转移矩阵、过程噪声输入矩阵和量测矩阵分别为

(13)

量测噪声协方差矩阵为

(14)

状态向量和预测协方差矩阵初始化为

(16)

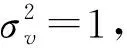
固定方位45°，仿真计算不同数据周期不同作用距离时矩形关联波门大小，统计如表2所示。从表中可以看出，距离越远关联波门越大，周期越长关联波门越大。

数据周期距离50 km距离100 km距离150 km距离200 km距离250 km2 s1 520 m×1 520 m2 820 m×2 820 m4 130 m×4 130 m5 450 m×5 450 m6 780 m×6 780 m4 s1 680 m×1 680 m3 000 m×3 000 m4 350 m×4 350 m5 700 m×5 700 m7 030 m×7 030 m6 s1 850 m×1 850 m3 200 m×3 200 m4 580 m×4 580 m5 950 m×5 950 m7 320 m×7 320 m8 s2 030 m×2 030 m3 420 m×3 420 m4 830 m×4 830 m6 230 m×6 230 m7 620 m×7 620 m10 s2 230 m×2 230 m3 660 m×3 660 m5 090 m×5 090 m6 520 m×6 520 m7 930 m×7 930 m12 s2 450 m×2 450 m3 910 m×3 910 m5 370 m×5 370 m6 820 m×6 820 m8 260 m×8 260 m

以4 s数据周期、距离100 km、方位45°、方位测量误差标准差0.3°为例，关联波门大小为Sxy=3 000 m×3 000 m，检测凝聚分辨单元设置为200 m×1.5°，计算关联波门内检测凝聚分辨单元个数为Nres=[Sxy/(200 m×1.5°×π/180°×100×103m)]=18，设置点迹级虚警率为Pf_plot∈[10-3,10-2]，不同点迹级检测概率下目标航迹平均跟踪周期数随点迹级虚警概率变化曲线如图2(a)所示。从图中可以看出，虚警概率越高，目标航迹平均跟踪周期数越小；目标检测概率越高，平均跟踪周期数越大。

以距离100 km、点迹级虚警概率Pf_plot=10-3为例，在其他参数不变的情况下，目标航迹平均跟踪周期数随数据周期变化曲线如图2(b)所示。从图中可以看出，随着数据周期增加，关联波门变大，波门内出现虚假的概率增加，航迹被虚假带偏从而跟丢的概率增加，平均跟踪周期数减少。

假设检测概率不随距离增加而变化，在4 s数据周期、点迹级虚警概率Pf_plot=10-3时，跟踪周期数随距离变化曲线如图3(a)所示。假定目标由近向远运动时，检测概率和虚警概率逐渐减小，从50 km运动到100 km，点迹级检测概率从0.9减小到0.7，点迹级虚警概率从10-3减小到0.7×10-3。此时跟踪周期数变化曲线如图3(b)所示。

4　结束语

本文在设定雷达目标跟踪过程中航迹维持或终止的条件下提出了一种目标跟踪周期数的近似评估方法，并对基于两坐标雷达匀速目标运动模型的Kalman滤波器跟踪性能进行了分析。仿真结果表明，在雷达数据周期和探测距离确定的情况下，目标航迹平均跟踪周期数主要取决于点迹级目标检测概率、虚警概率和雷达方位测量精度。检测概率越高，平均跟踪周期数越大；虚警概率越低，平均跟踪周期数越大；雷达精度越高，平均跟踪周期数越大。本文提出的基于Kalman滤波的目标跟踪周期数计算方法可为复杂背景下目标跟踪滤波算法参数优化提供理论支撑，对于两坐标雷达目标跟踪加速运动模型和三坐标雷达目标跟踪周期数的计算也可以采用本文的思路和方法进行分析。