温度影响下DNA分子欧拉临界力模拟研究

辜凌云，张敏，周勋

（1.贵州师范大学 物理与电子科学学院，贵州贵阳 550025；2.贵州大学 大数据与信息工程学院，贵州贵阳 550025）

0 引言

DNA力学性质一直以来都是研究的重点，原因之一是其在生物学行为中发挥着重要作用，如DNA的复制、转录、重组等。长期以来关于DNA性质的研究大多集中于碱基序列的生物化学性质，对物理性质研究较少，导致其力学相关性质认识有所不足。

随着单分子操纵技术的发展，实验上通常利用原子力显微镜（AFM）、磁镊子（MT）、光镊子（OP）等技术[1-4]对单个DNA分子施加力的作用，测量其物理性质。而相对于实验，利用计算机从理论上对DNA分子进行模拟，也是表述其性质的有效手段。

DNA分子拥有高曲率是其生物活性的基础，DNA发生弯曲在许多生理过程中是不可或缺的一部分，DNA欧拉临界力作为DNA分子开始发生弯曲时所需的力，对其进行探究十分有意义。因为DNA分子临界力与弯折刚度有关，而实验表明弯折刚度会受温度影响，当温度范围在3℃到53℃时，弯折刚度与温度之间的关系可以近似表示为g=(3.19×10-19-T·4.14×10-22)erg·cm[5]，所以十分有必要探究温度对DNA欧拉临界力的影响。此外根据弹性理论[14]可知，DNA分子欧拉临界力还与DNA链长有关，所以同样有必要对不同长度下的DNA欧拉临界力进行研究，但是想要通过实验直接测量DNA分子弯折力十分困难，而采用计算模拟的方法则能很好的解决这一问题。

通过对理论和实验结果的分析[6]，我们基于蠕虫链模型（Worm-Like Chain Model）[7]和胡克弹簧模型（Hooke spring model），建立可表征DNA微力学性质的力学模型（图1），此基础上考虑DNA分子的弯折和拉伸，利用Monte Carlo方法进行模拟。最终通过模拟，给出不同长度、温度下的DNA分子力以及临界力。

1 理论模型及计算方法

1.1 DNA微力学模型

研究通过结合目前的单分子实验，建立如图1所示的DNA微力学模型[8]，主要考虑DNA分子弯折能、DNA分子片段弹性能以及弹簧的弹性能，体系总能量表示为：

Et为DNA分子弯折能，利用蠕虫链模型[9]表征。DNA分子每个片段取向矢量为t^i，相邻片段取向间的夹角为θ，弯折刚度为g，则DNA分子弯折能可以表示为：

对于DNA受温度影响，这里主要考虑温度对DNA分子驻留长度的影响，弯折刚度g与DNA驻留长度lp存在关系lp=g/kBTkB为玻尔兹曼常数，T为温度）[10][11]，代入关系g=(3.19×10-19-T·4.14×10-22)erg·cm[5]，则驻留长度可以表示为，又根据g=lp，b为DNA分子的片段长度，对于长度小于500个碱基对的DNA分子，b约为1nm，即g=lp，可以得到：

b为DNA分子片段的总弹性能，每个片段原长度为bnm，改变分子构象后，片段的长度变为binm，DNA分子弹性能可表示为：

k1为双链DNA分子片段的弹性模量[12]，约为1200pN/nm。

El为连接在DNA分子首末两端的弹簧所具有的的弹性能，如图1所示，弹簧原长度为l0，〈R〉k1为DNA分子构象的首末端距，弹簧的弹性能可表示为：

k2为限制弹簧的弹性模量[12]，约为1200pN/nm。

图1 DNA微力学模型示意图

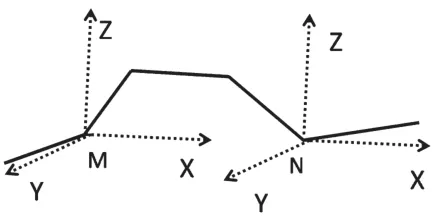
图2 构象变化方法

1.2 Monte Carlo模拟[13]及Metropolis判据

在模拟过程中，产生DNA分子新构象的方法如图2所示，图2中为DNA分子链中的部分片段，模拟中随机选取DNA链上的点（M或N）沿着xyz方向进行扰动产生新的DNA分子构象，扰动的幅度由模拟产生的随机数进行控制。

抽样过程采用了Metropolis判据，将原构象能量Eold与新构象能量Enew进行对比。若新构象能量小于原构象能量（Enew＜Eold），则新构象完全被接受（p=1）；若新构象能量大于原构象能量（Enew＞Eold），则将计算其概率p=exp[(Eold-Enew)/kBT]，并与随机数χ(0～1)进行比较，若p＜χ则被接受，反之不接受，其目的是为了使模拟能够遍历所有可能情况。

2 结果与讨论

2.1 DNA分子力随链长变化

常温下，DNA驻留长度lp为50nm，根据弹性理论[14]，可以由公式fcr=π2E/L2计算其理论临界力大小，其中E为弹性模量，I为转动惯量，L为长度。对DNA分子链，可以将其视为弹性杆[15]，即EI=lpkBT，理论上DNA分子链的欧拉临界力可以表示为：

模拟得到的DNA链的分子力则可以通过如图1所示，连接在其两端的弹簧所受力来表征。模拟过程中不断改变弹簧的长度，当弹簧长度接近DNA分子长度，即弹簧长度与DNA链长比值接近1时，力会出现转变，转变点的力即为该长度DNA分子的欧拉临界力，弹簧力可以表示为：

〈R〉为DNA分子链的首末端距，k2为弹簧的弹性模量，l0为弹簧的原长度。

基于上述理论，我们分别对长度为5 nm、9 nm、12 nm、15 nm、20 nm的DNA进行模拟，通过改变弹簧的长度，得到对应的欧拉临界力。将临界力的理论值与模拟值比较，得到表1的结果，其模拟值与理论值非常接近，说明模拟工作是可靠的。

表1 不同长度DNA欧拉临界力理论值与模拟值对比

2.2 温度对临界力的影响

对于DNA受温度的影响，主要由式（3）中弯折刚度与温度的关系体现。如图4，是DNA长度为9nm时，连接在其两端的弹簧所受力随温度的变化情况，曲线从上至下分别为10℃、20℃、30℃、40℃、50℃。从图中可以看出，温度越高，DNA分子受力越小，其转折处对应的欧拉临界力也越小。

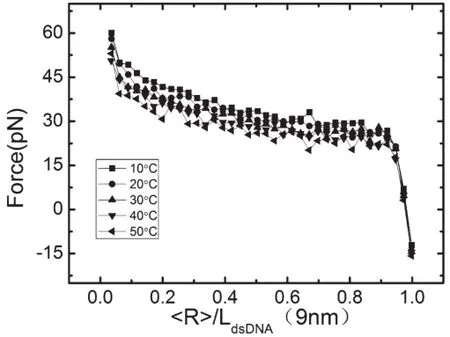
图4 温度对9 nmDNA分子力的影响

图5 不同长度下温度对DNA欧拉临界力的影响

图5为不同长度的DNA，其欧拉临界力随温度的变化情况，从上至下其长度依次对应9 nm、15 nm、20 nm。结果显示随着温度升高，欧拉临界力都呈现出逐渐减小趋势，并且DNA链长度越长，临界力波动越小，折线更加平滑，说明长度越长DNA分子欧拉临界力受温度影响越小。

3 结论

模拟结果显示，基于蠕虫链模型和胡克弹簧模型搭建的DNA微力学模型能够有效表征DNA的力学性质，得到的模拟值与理论值符合良好,说明DNA分子具备与弹性杆相类似的力学性质，可以用弹性理论进行解释。通过对不同温度下的DNA分子力进行模拟，结果显示随着温度升高，DNA分子力下降，不同长度下的所对应的DNA欧拉临界力均呈现减小的趋势，并且长度越短受温度影响越明显。

[1]Binnig G, Quate C F, Gerber C. Atomic force microscope[J]. Physical review letters, 1986, 56(9): 930.

[2]Gosse C, Croquette V. Magnetic tweezers: micromanipulation and force measurement at the molecular level[J]. Biophysical journal, 2002,82(6): 3314-3329.

[3]Wang M D, Yin H, Landick R, et al. Stretching DNA with optical tweezers[J]. Biophysical journal, 1997, 72(3): 1335-1346.

[4]Neuman K C, Nagy A. Single-molecule force spectroscopy: optical tweezers, magnetic tweezers and atomic force microscopy[J]. Nature methods, 2008, 5(6): 491.

[5]Geggier S, Kotlyar A, Vologodskii A. Temperature dependence of DNA persistence length[J]. Nucleic acids research, 2010, 39(4): 1419-1426.

[6]Shroff H, Reinhard B M, Siu M, et al. Biocompatible force sensor with optical readout and dimensions of 6 nm3[J]. Nano letters, 2005, 5(7):1509-1514.

[7]Flory P J, Volkenstein M. Statistical mechanics of chain molecules[J].Physics Today, 1970, 23(5):71-71.

[8]刘艳辉. 微环 DNA 微力学, 拓扑性质及 DNA 凝聚机制研究[D].贵州大学, 2009.

[9]Colby R H, Rubinstein M. Polymer physics[J]. New-York: Oxford University, 2003: 274-281.

[9]De Groot S R, De Groot S R. Thermodynamics of irreversible processes[M]. Amsterdam: North-Holland, 1951.

[10]Schellman J A. Flexibility of DNA[J]. Biopolymers, 1974, 13(1): 217-226.

[11]Cocco S, Marko J F, Monasson R. Theoretical models for singlemolecule DNA and RNA experiments: from elasticity to unzipping[J].Comptes Rendus Physique, 2002, 3(5): 569-584.

[12]刘艳辉, 胡林. DNA 微环拓扑性质的 Monte Carlo 模拟[J]. 计算物理, 2009, 26(1): 152-158.

[13]Timoshenko S. Theory of Elastic Stability[M]. Tata McGraw-Hill Education, 1970.

[14]Hinner B, Tempel M, Sackmann E, et al. Entanglement, elasticity, and viscous relaxation of actin solutions[J]. Physical Review Letters, 1998,81(12): 2614.