A Note on the Generalized and Universal Associated Legendre Equations∗
Keegan L.A.Kirk, Kyle R.Bryenton, and Nasser Saad
School of Mathematical&Computational Sciences,University of Prince Edward Island,550 University Avenue,Charlottetown,PEI C1A 4P3,Canada
1 Introduction
Recently,the Universal Associated Legendre Polynomials
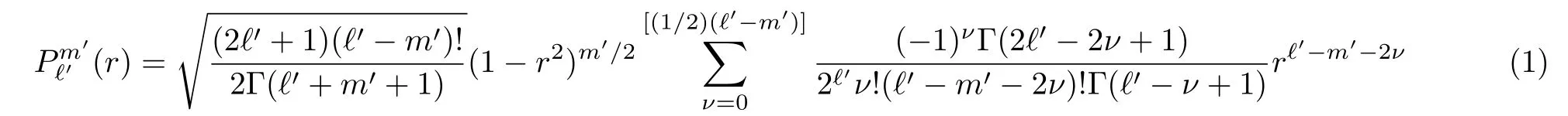
has been the subject of many interesting studies.[1−7]These polynomials are solutions to the differential equation(see Ref.[2]and the references therein):

in which b=0,m′=Through partial-fraction decomposition of the rational coefficient of the Pm′ℓ′(r)term,Eq.(2)is shown to be a slight modification of the well-known Generalized Associated Legendre Equation[8−19]
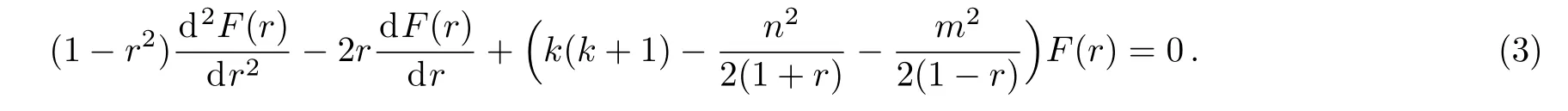
The differential equation(3)was introduced first by Bateman in his analysis of the harmonic equations(Ref.[8],page 389).Following Bateman’s work,this was later intensively studied in a series of research articles by Kuipers and Meulenbeld for complex-valued parameters k,m,and n.[9−17]The recent book of Virchenko and Fedotova[19]was devoted to the subsequent development of the theory of the Generalized Associated Legendre Functions and their applications.
As we shall prove in the present work,both differential equations(2)and(3)are members of a more general class of differential equations characterized by

where aj,bj,j=1,2,3,c3are real parameters and ξ1 The exact solutions of the differential equation(4)are given,along with their relations to the published solutions of the Generalized and Universal Associated Legendre Differential Equations(2)and(3).New solvable classes of differential equations useful for the analysis of quantum systems are obtained.[20−22] The differential equation(4)has three regular singular points,r ∈ {ξ1,ξ2,∞}with exponents µ1, µ2,andµ∞,respectively,determined as the roots of the indicial(quadratic)equations: According to the classical theory of ordinary differential equations,[23]Eq.(4)is reducible to the hypergeometric equation.To this end,the general solutions of Eq.(4)take the form where the exponents µ1and µ2are evaluated using Eqs.(5)and(6)respectively.The substitution of Eq.(8)into Eq.(4)yields the following hypergeometric-type equation for the function f≡f(r): Employing the Möbius transformation,z=(αr+ β)/(γr+ δ),for αδ− βγ0,yields Thus,if γ=0,the change of variables r→z≡z(r)transforms Eq.(10)into an equation of the same type as that of Eq.(9).This in turn implies To express the solutions of this equation in terms of hypergeometric functions,one must impose either of the following necessary conditions on α, β,and δ: Should we impose the conditions as given(i),Eq.(11)reduces to(denoting f→) (z)=z1−2µ2+(b1+a1ξ2)/(ξ2−ξ1) More precisely,the analytic solutions of the differential equation(4),for arbitrary constants A1and A2,are where Equivalently,the exact solutions of the differential equation(4)may also be expressed as(denoting f→) As a result,we are able to obtain Eq.(18)from Eq.(21)and vice versa.This relationship may be confirmed using the linear transformation(Ref.[24],Eq.(15.8.4)): After some simplification,it follows that For the second solution(17),we may again apply Eq.(24)to obtain To obtain the expression in terms ofthe Pfaff transformation(Ref.[24],Eq.(15.8.1)), must be used for the hypergeometric functions on the right-hand side of Eq.(26).It is sufficient to focus on either one of the solution sets. This section serves to demonstrate the relationship between the differential equations(3)and(4).First denote then,using partial-fraction decomposition,Eq.(4)reads Using Eq.(28),the indicial equations(5)and(6)may be expressed as Thus,Eq.(29)reduces to with the exact solutions,determined via Eq.(21),given by: as found earlier by Kuipers et al.forµ1=n/2 andµ2=−m/2.In this case equation(30)reads For ξ2= −ξ1=1,Eq.(33)reduces to the Generalized Associated Legendre Differential Equation.Different choices of ξ1and ξ2give rise to other interesting classes of differential equations,(e.g. ξ1=0, ξ2=1).The mathematical properties of these other classes(such as the weight-function,the recurrence relation,the orthogonality conditions,etc.)will be the focus of future work. To establish the connection between the solutions of the differential equation(4)and that of the Universal Associated Legendre Equation(2)as given by Eq.(1),we express Eq.(1)in terms of the hypergeometric function.Using the Legendre Duplication Formula,Γ(2z)=22z−1Γ(z)Γ(z+1/2)/Eq.(1)can be written as Further,by means of the Pochhammer identity Γ(z − ν)=(−1)νΓ(z)/(1 − z)ν,we obtain With the assumption that −(1/2)(ℓ′− m′)or(1/2)(1 − (ℓ′− m′))=0,−1,−2,...,this equation may now be written in terms of the hypergeometric equation with the understanding that the limit of the right-hand side is well-defined as r→0.Since it easily follows that The identity(Ref.[24],Eq.(15.8.6)) implies With a1=2(µ1+µ2−1),the differential equation(4)reads after an application of partial-fraction decomposition, Using the identity(Ref.[24],Eq.(15.8.20)): the solution of Eq.(39),namely, can be written as Using the identity(Ref.[24],Eq.(15.8.7)), and assuming it follows that c=1/2.Finally,the solution(41)now reads which reduces,up to a multiplicative constant,to the solution(38)for b1=0, ξ1= −1 and ξ2=1. The classical Generalized and the recent Universal Associated Legendre Equations are members of the more broad class of differential equations given by Eq.(4).We established the hypergeometric solutions of this class of equations and demonstrated that they lead to the Generalized and Universal Associated Legendre hypergeometric solutions.These new solutions open the door for further compelling studies,including the examination of their mathematical properties and the investigation of their applicability to problems in mathematical physics. [1]Chen Chang-Yuan,You Yuan,Lu Fa-Lin,et al.,Commun.Theor.Phys.62(2014)331. [2]Chang-Yuan Chen,Fa-Line Lu,and Dong-Sheng Sun,Appl.Math.Lett.40(2015)90. [3]Chen Chang-Yuan,You Yuan,Lu Fa-Lin,et al.,Commun.Theor.Phys.66(2016)158. [4]Chen Chang-Yuan,Lu Fa-Lin,Sun Dong-Sheng,et al.,Ann.Physics:Elsevier 371(2016)183. [5]G.Yañez-Navarro,Guo-Hua Sun,et al.,Commun.Theor.Phys.68(2017)177. [6]G.Yañez-Navarro,Guo-Hua Sun,Dong-Sheng Sun,et al.,J.Math.Phys.58(2017)052105. [7]Wei Li,Chang-Yuan Chen,and Shi-Hai Dong,Adv.High Energy Phys.2017(2017)1,doi:10.1155/2017/7374256. [8]H.Bateman,Partial Differential Equations of Mathematical Physics,Cambridge University Press,Cambridge(1932). [9]L.Kuipers and B.Meulenbeld,Proc.Kon.Ned.Ak.V.Wet.Amsterdam 80(1957)436. [10]L.Kuipers and B.Meulenbeld,Proc.Kon.Ned.Ak.V.Wet.Amsterdam 80(1957)444. [11]L.Kuipers,Math.Scand.6(1958)200. [12]L.Kuipers and B.Meulenbeld,Arch.Math.66(1958)394. [13]L.Kuipers and B.Meulenbeld,Proc.Konkl.Nederl.Akad.Wet.Ser.A 61(1958)557. [14]L.Kuipers and B.Meulenbeld,Proc.Kon.Ned.Akad.Wetensch.;Ser.A 61(1958)330. [15]L.Kuipers and B.Meulenbeld,Proc.Kon.Ned.Akad.Wetensch.Ser.A 61(958)186. [16]L.Kuipers and B.Meulenbeld,Arch.Math.F 66(1958)394. [17]L.Kuipers,Monatsschr.Math.63(1958)24. [18]N.A.Virchenko and I.A.Fedotova,J.Math.Sci.69(1994)1395. [19]N.A.Virchenko and I.A.Fedotova,Generalized Associated Legendre Dunctions and Their Applications,World Scientific,Singapore(2001). [20]L.K.Sharma,Proc.Indian Nat.Sci.Acad.A 36(1970)239. [21]I.A.Khan,Indian J.Pure Appl.Math.4(1973)90. [22]H.Ciftci,R.L.Hall,N.Saad,and E.Dogu,J.Phys.A:Math.Theor.43(2010)415206. [23]Earl A.Coddington and N.Levinson,Theory of Ordinary Differential Equations,McGraw-Hill,New York(1955). [24]F.W.J.Olver,A.B.Olde Daalhuis,D.W.Lozier,et al.,NIST Digital Library of Mathematical Functions,http://dlmf.nist.gov/15.8,Release 1.0.17 of 2017-12-22.2 Exact Solutions



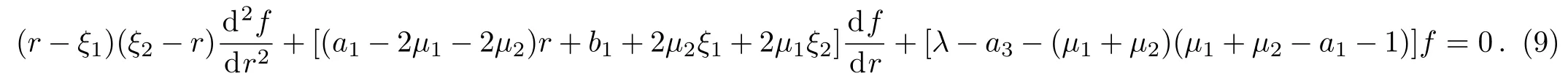













3 Connection with the Generalized Associated Legendre Equation






4 Connection with the Universal Associated Legendre Equation
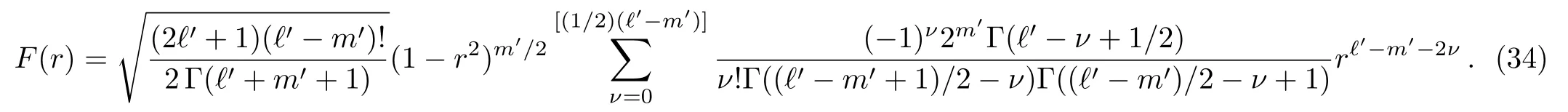

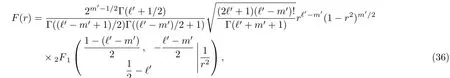
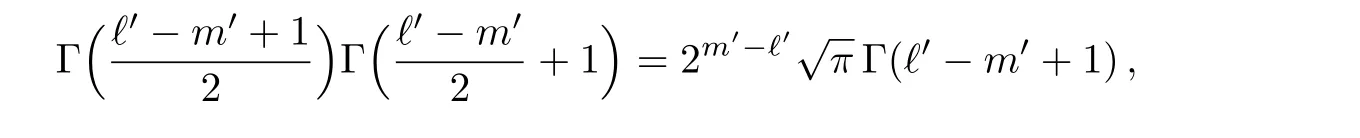

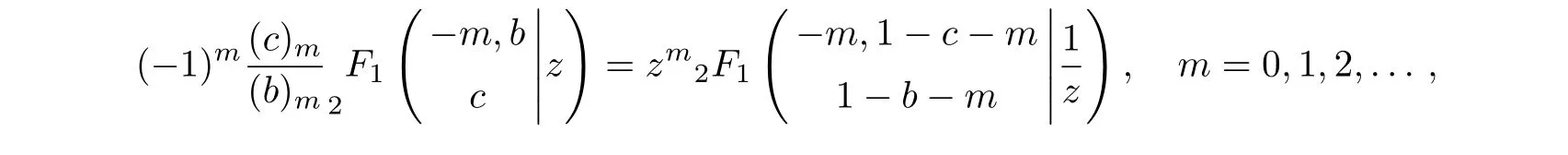

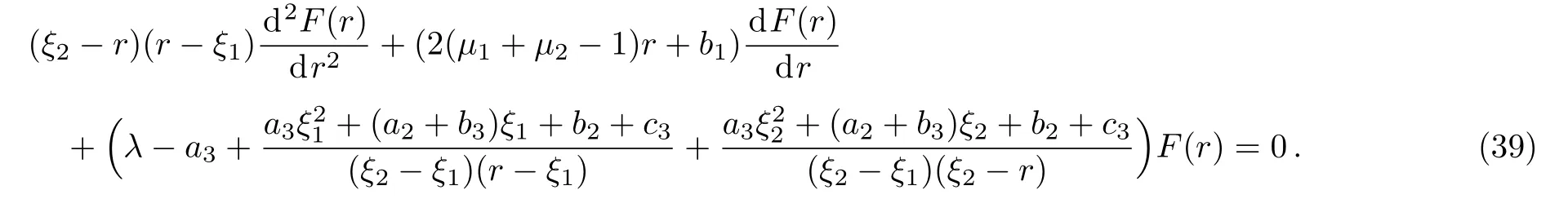







5 Conclusion
 Communications in Theoretical Physics2018年7期
Communications in Theoretical Physics2018年7期
- Communications in Theoretical Physics的其它文章
- Electron Correlations,Spin-Orbit Coupling,and Antiferromagnetic Anisotropy in Layered Perovskite Iridates Sr2IrO4∗
- The Three-Pion Decays of the a1(1260)∗
- A New Calculation of Rotational Bands in Alpha-Cluster Nuclei
- Upshot of Chemical Species and Nonlinear Thermal Radiation on Oldroyd-B Nano fluid Flow Past a Bi-directional Stretched Surface with Heat Generation/Absorption in a Porous Media∗
- Detection of Magnetic Field Gradient and Single Spin Using Optically Levitated Nano-Particle in Vacuum∗
- Transverse Transport of Polymeric Nano fluid under Pure Internal Heating:Keller Box Algorithm
