二滩水轮发电机转子匝间短路故障的电气特征及在线监测
郭玉恒,王思良,任保瑞,郝亮亮,陈 俊,张琦雪
(1. 二滩水力发电厂,四川省攀枝花市 617000;2.北京交通大学电气工程学院,北京市 100044;3.南京南瑞继保电气有限公司,江苏省南京市 211102)
0 引言
水轮发电机故障及异常工况的在线监测是目前的研究热点[1],转子绕组匝间短路是大型水轮发电机常见的一种电气故障,近年来对该故障的报道屡见不鲜。轻微的短路故障不会给发电机带来严重的后果,但若不对其进行监测而任其不断恶化,将会导致励磁电流增大、输出无功能力降低及机组振动加剧等不良后果。故障还有可能恶化为发生在励磁绕组与转子本体之间的一点或两点接地故障,严重时还可能会烧伤轴颈、轴瓦,给发电机组及电力系统的安全稳定运行带来巨大的威胁[2]。
二滩水电站的水轮发电机也曾发生转子绕组匝间短路故障,在2015年对1号机组进行交流阻抗及功率损耗测量中,经过反复检查确定了共18个磁极交流阻抗值偏低,存在匝间短路现象。随后电厂对6个交流阻抗值最低的磁极进行了更换,但其余12个磁极交流阻抗值仍然偏低,需要择机进行更换。为避免这些存在安全隐患的磁极故障恶化,需要进行持续有效地监测。
除因发电机转子绕组自身加工工艺不良以及绝缘缺陷等引起的转子匝间短路外,转子高速旋转时励磁绕组承受的离心力会造成各绕组之间的挤压及移位变形、转子绕组的热形变、通风不良引起的局部过热及金属异物等,是实际中导致转子匝间短路故障的重要原因,且多在发电机实际运行中发生。
如果能够在发电机运行中实现对二滩转子绕组匝间短路故障的在线监测,及时发现处于萌芽期的小匝数早期故障,监视其发展并确定是否需要检修,就能避免轻微的故障恶化成为严重的匝间短路或转子接地故障。这对保障发电机的安全运行具有重要的意义,有必要深入研究并实现二滩水电站的水轮发电机转子绕组匝间短路故障的在线监测。
本文首先基于交流电机的多回路分析法[3],实现了对二滩水轮发电机转子匝间短路故障的数字仿真,并据此得到了故障的电气特征。采用故障录波TA所提供的定子分支电流和相电流,得到了定子不平衡电流,实现了故障的在线监测。开发了在线监测装置,根据相关录波数据对监测定值进行了整定,灵敏性分析表明,装置能实现对故障的灵敏监测。
1 二滩发电机转子匝间短路故障的仿真
1.1 转子匝间短路故障的数学模型
水轮发电机的转子绕组发生匝间短路故障后,转子绕组将被分为正常绕组和故障附加绕组。所以,反映故障的数学模型首先应能体现出故障转子绕组拓扑结构的差异。除此之外,虽然定子绕组仍然是正常的,但转子故障附加绕组会产生空间谐波磁场,模型应能考虑该谐波磁场在正常的定子相绕组内部产生不平衡电流。
如图1所示的两分支发电机,以实际的5个定子回路(而非相绕组)、转子绕组的正常回路和故障附加回路、所有实际的阻尼网型回路(而非等效d、q轴绕组),列出以定、转子所有回路电流为变量的状态方程:

式中I'——定子和转子各回实际路的电流;
M'——回路电感阵;
R'——回路电阻阵;
RT—— 常数阵,与电网线路及变压器的漏感、电阻和励磁绕组的电感及电阻有关;
E—— 由电网电压和励磁电压组成,是已知的列向量。
式(1)为同步发电机转子匝间短路故障的暂态仿真数学模型,该模型是时变系数的微分方程组,求解该模型可以得到从故障发生到进入稳态的整个过渡过程。但在求解之前,还需要求解回路电感M'阵,特别是与故障转子绕组相关的电感参数。多回路分析法从单个线圈出发,能够深入故障绕组内部,首先计算与单个线圈有关的电感参数,再按实际的绕组叠加组成与回路有关的电感参数[4]。基于该模型可对二滩水轮发电机发生的转子匝间短路故障进行仿真。
1.2 二滩发电机转子绕组匝间短路故障的仿真结果
本文基于多回路分析法建立了二滩水轮发电机的暂态仿真模型,二滩发电机的主要参数如表1所示。
图2为二滩水轮发电机发生转子绕组19%匝间短路故障的仿真波形,限于篇幅仅列出定子a1分支、定子相电流及励磁电流波形。
由图2可见:故障前后定子各分支电流较故障前明显增大,但定子相电流基本保持不变;故障后励磁电流的直流分量明显增大,且出现了正常运行时没有的谐波分量。由于图1比较密集,图3分别把对应的故障前和故障后的稳态波形进行了更为清晰的对比(左图是故障前稳态,右图是故障后稳态)。

图1 转子绕组发生匝间短路故障时的发电机各回路(a)实际的定子回路示意图;(b)转子绕组的正常回路和故障附加回路;(c)实际的阻尼网型回路Fig.1 Generator circuits in the case of rotor winding interturn short circuit fault(a)Schematic diagram of stator circuits;(b)Normal circuit and fault additional circuit of rotor winding ;(c)Diagram of damping circuits
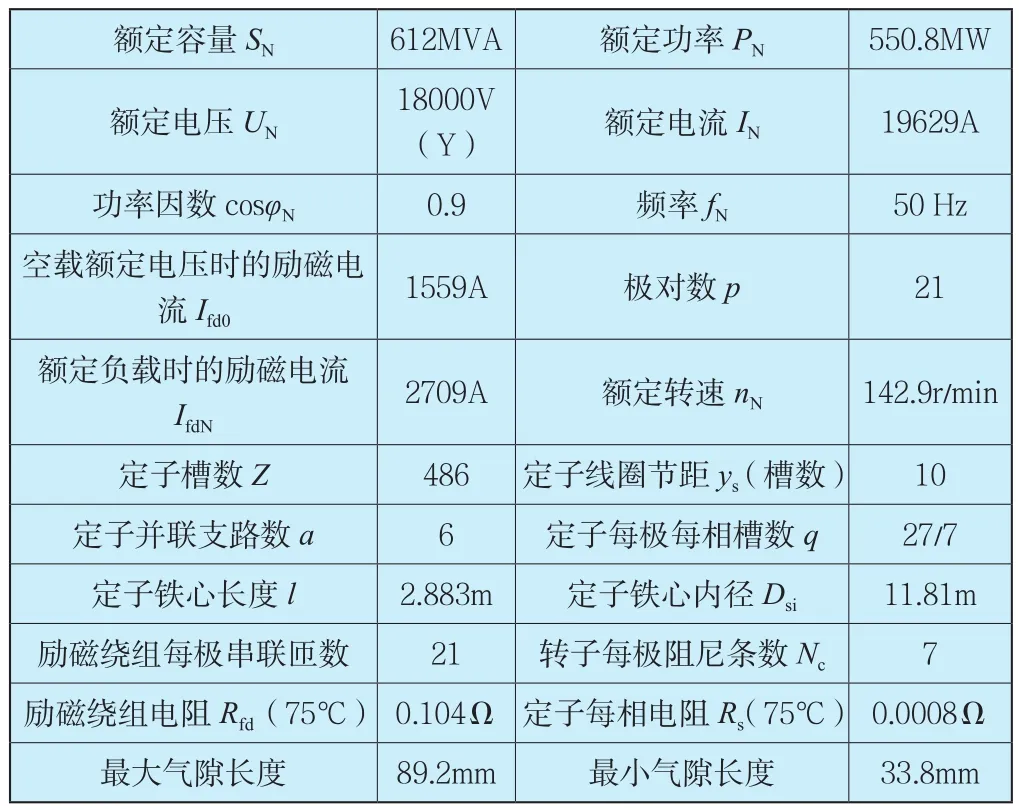
表1 二滩水轮发电机的主要参数Tab. 1 Main parameters of Ertan hydrogenerator

图2 二滩水轮发电机转子绕组匝间短路故障的过渡过程波形(a)定子a1分支电流;(b)定子a2分支电流;(c)定子三相电流;(d)励磁电流Fig.2 Transient process waveforms of rotor winding inter-turn short circuit fault of Ertan hydrogenerator(a)Stator a1 branch current;(b)Stator a2 branch current;(c)Stator three-phase currents;(d)excitation current
由图3(a)可更清楚地看到,故障后定子分支电流不仅大于正常运行,且出现了正常运行时没有的谐波分量;由图3(b)可见,故障后定子两分支间出现了明显的谐波差流;而由图3(c)可见,虽然励磁电流出现了谐波分量,但谐波分量明显较直流分量小很多。
2 二滩发电机转子匝间短路的电气特征及机理分析
2.1 二滩发电机转子绕组匝间短路电气特征的定量分析
前文仅从仿真波形上通过观察得出了故障电流的一些特点,为进一步分析二滩水轮发电机发生转子绕组匝间短路的故障特征,对故障前后的各电流稳态波形进行了FFT(快速傅里叶)分析,如表1所示。表中定子a1分支电流从4/21~16/21次及22/21以上次数的谐波、励磁电流2以上次数的谐波不再列出。
从仿真波形及表2可以看到,二滩水轮发电机发生转子绕组匝间短路后的故障特征如下:
(1)故障前后定子相电流大小基本不变,且均以基波为主。
(2)故障后定子分支出现正常时不存在的1/21、2/21等一系列与极对数相关(二滩发电机极对数为21)的分数次谐波电流。
(3)正常运行时分支差流为零,故障后出现了明显的分支谐波差流(也为1/21、2/21等分数次谐波)。
(4)故障后励磁电流的直流分量变大,并且出现了幅值很小的离散次数的分数次谐波电流。
2.2 二滩发电机转子绕组匝间短路电气特征出现的机理
发生在转子绕组的匝间短路首先会造成励磁绕组各极下的结构差异。如图4所示,假设第1极下的转子绕组发生w匝短路,于是在空间电角度坐标系下的[-pπ,pπ]区间内,故障励磁绕组产生的磁动势(x)为:


图3 二滩水轮发电机正常运行及转子绕组匝间短路故障的稳态波形对比(a)定子a1分支电流;(b) 定子a1和a2分支差流;(c) 励磁电流Fig.3 Comparison of Ertan hydrogenerator steady-state waveforms between normal operation and rotor winding inter-turn short circuit fault(a)Stator a1 branch current;(b)Stator a1 and a2 branch differential current;(c)Excitation current
式中k——谐波次数;
Fk——第k谐波的幅值。


图4 水轮发电机故障励磁绕组产生的磁动势示意图Fig.4 Schematic diagram of magnetomotive force generatedby fault excitation winding of hydrogenerator
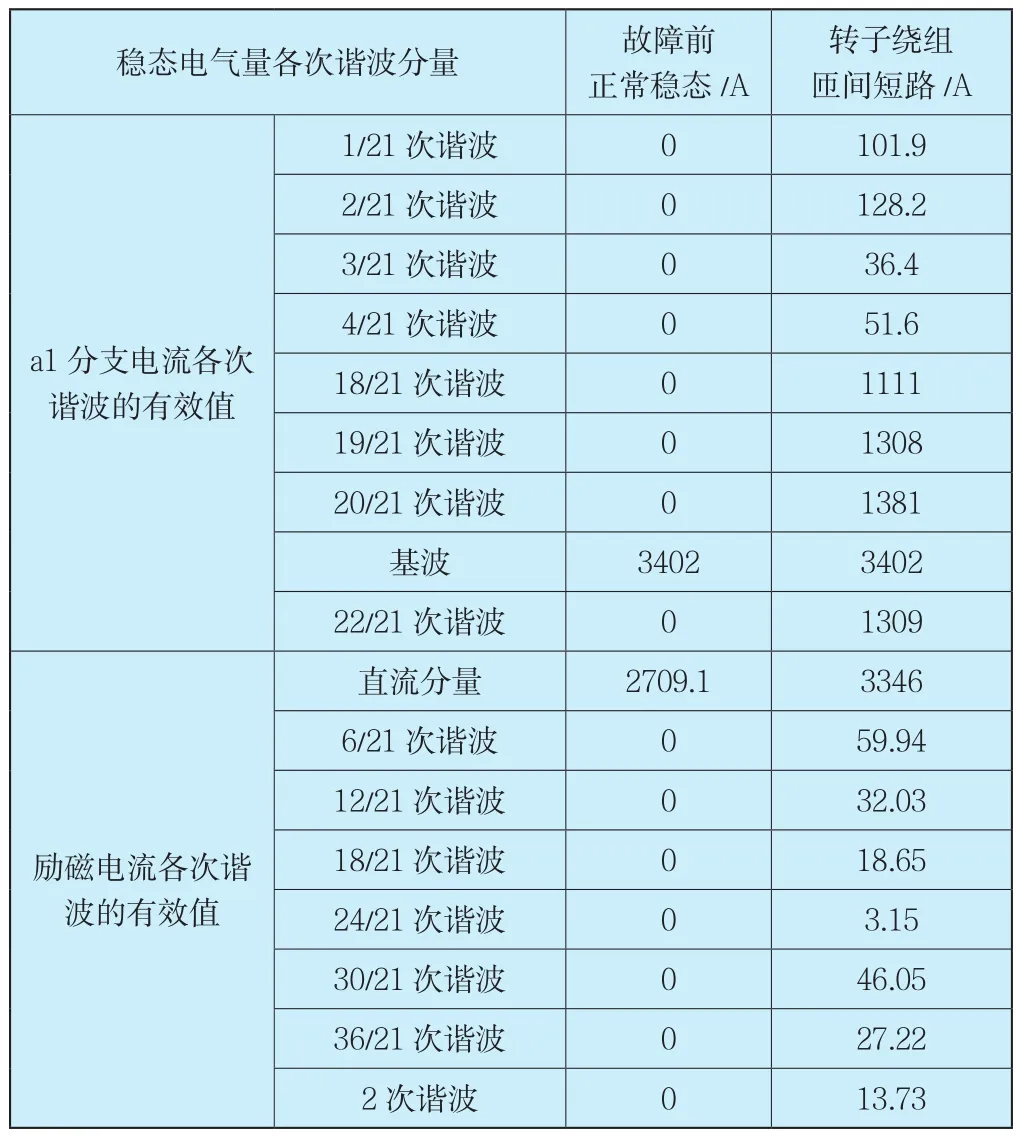
表2 二滩水轮发电机发生转子绕组匝间短路的稳态电流傅里叶分析结果Tab.2 Steady-state current’s Fourier analysis of rotor winding inter-turn short circuit in Ertan hydrogenerator
当k为偶数时,Fk等于零。因此,故障励磁绕组产生的磁动势仅含空间基波、奇数次谐波及1/p、2/p等分数次谐波。这些磁动势作用于不均匀的气隙仍产生基波、奇数次谐波及1/p、2/p等分数次谐波。基波和奇数次空间谐波磁场在定子同相各分支感应相同时间相位的基波和奇数次谐波电流;分数次空间谐波磁场在定子同相各分支感应相位不同的电动势,进而产生与极对数相关的谐波不平衡电流。对于二滩发电机而言,由于其极对数为21,故产生的是1/21、2/21等分数次谐波电流。
而正是因为定子谐波不平衡电流在相绕组的内部产生,各分支不平衡电流之和为零,因此相电流主要还是以基波为主。
由于故障会导致转子绕组的有效匝数变少,励磁回路的转子绕组电阻减小,在励磁电压不变的情况下,励磁电流的直流分量会增加。而由于与极对数有关的定子谐波不平衡电流会产生谐波电枢反应磁动势,进而在发电机的转子绕组感应出一系列的谐波电流。对该谐波电流次数的理论分析方法可见参考文献[5],限于篇幅不再一一赘述。
3 二滩水轮发电机转子匝间短路故障的在线监测
3.1 监测对象的选取
若要实现对转子绕组匝间短路故障的在线监测,所选取的监测对象需满足两个基本要求:首先特征量不能太小,特征量太小必然会给监测带来难度;其次,需保证所选取监测对象的特征具有排他性,是转子绕组匝间短路故障所独有。
从表2可见,故障后的励磁电流交流分量十分小。这是因为阻尼绕组的存在,故障引起的转子故障成分主要分布在阻尼电流中。因此,励磁电流不适宜作为监测对象。
同步发电机发生定子机端外部短路时,定子稳态电流中仅存在基波及3、5等奇数次谐波;转子稳态电流中仅存在直流分量及2、4等偶数次谐波。当发生定子内部短路(包括匝间短路、相间短路)时,虽然短路的定子绕组也会产生分数次和偶数次空间谐波磁场,但该磁场仅在定子中感应基波及奇数次谐波电流。当发生定子分支开焊故障时,定子和转子也分别出现与定子内部短路相同的谐波。当发生定子单相接地故障时,仅定子机端会出现基波零序电压及3次谐波电压,而不会对定子分支电流产生明显影响。
由文献[6]可知,当发生转子偏心(主要指静偏心)故障时,定子分支不平衡电流也仅为基波及奇数次谐波,而仍不会产生偶数次及分数次谐波。发生在转子的一点接地故障不会引起气隙磁场的畸变,在定子侧无反应。而转子两点接地故障同样导致励磁绕组部分短路,其引起的定子不平衡电流特征与转子绕组匝间短路故障相同。但GB/T 14285—2006《继电保护和安全自动装置技术规程》中要求1MW 及以上的发电机均应装设专用的转子一点接地保护装置,现场发生两点接地故障的可能性较小。并且由于保护原理的不完善,目前的发电机并无专用的转子两点接地故障保护。考虑到转子两点接地故障的危害性,若发生了转子两点接地故障,并导致了转子绕组匝间短路故障监测的报警也是合理的。
另外,某些异常工况(如系统振荡)也可能引起定子各分支及相电流的偶数及分数次谐波。但此时引起的定子电流在同相各分支是相等的,不会导致相绕组内部不平衡电流的产生。
综上,发生在定子和转子的各种故障及异常工况均不会产生定子相绕组内部1/21、2/21等与极对数相关的一系列分支不平衡电流,该电气特征为二滩水轮发电机转子绕组匝间短路故障的独有特征,且从仿真中可以看出该特征在故障后十分明显。
3.2 基于定子稳态不平衡电流有效值的在线监测原理及装置
由于定子稳态不平衡电流中的这些分数次谐波均由转子绕组匝间短路故障引起,且不同于其他故障以及系统振荡等不正常状态。如果将该不平衡电流的稳态总有效值而非某一单次谐波有效值作为参考量,可包含所有的故障特征量,实现故障特征的最大程度提取[7]。实际中采用不平衡电流滤除基波及奇数次谐波后的其他不平衡电流总有效值作为监测判据。
PCS-988A发电机转子绕组匝间故障监测装置检测发电机定子绕组分支(组)TA及单元件横差TA,通过计算定子不平衡电流的有效值,实现发电机转子绕组匝间故障的监测。PCS-988A的部署视图如图5所示。装置可接入机端TV、机端TA、励磁变压器TA、中性点TA以及单元件横差TA。
图6为所研发的转子匝间故障监测装置的面板图。

图5 PCS-988A的部署视图Fig.5 Deployment view of PCS-988A

图6 PCS-988A的产品面板图Fig.6 Product panel diagram of PCS-988A
4 二滩发电机转子匝间短路在线监测装置的定值整定及灵敏性分析
图7是2017年3月17号对4号机组正常运行时单元件差流io1和io2最新的录波数据,该发电机的有功功率约为0.8p.u.,无功功率约为0.02p.u.。
经过离线的傅里叶分析,可知:
横差1的不平衡电流总有效值为0.62A,基波为0.50A,3次谐波为0.12A,其他谐波有效值为0.35A;横差2的不平衡电流总有效值为0.65A,基波为0.51A,3次谐波为0.2A,其他谐波有效值为亦为0.35A。
监测定值应按躲过发电机空载及并网额定运行情况下的最大不平衡电流整定。从可靠防误动的角度,并且考虑到发电机未满载,乘以2倍的可靠系数,取单元件差流Ⅰ段定值监测定值为:
0.35×2=0.70(A)
单元件差流Ⅱ段定值考虑乘4倍可靠系数,取为:
0.35×4=1.40(A)
在投运初期,为可靠防误报警,Ⅰ段延时取为90s;Ⅱ段延时取60s。当监测Ⅰ段报警时应密切关注发电机的运行情况,而当监测Ⅱ段报警时应尽快转移机组负荷平稳停机进行检查。
为定量描述监测原理反应转子绕组匝间短路故障的灵敏性,定义监测的灵敏系数为转子绕组匝间短路故障时定子不平衡电流总有效值与监测定值的比值。显然对于不同短路匝数的故障,监测的灵敏系数也不同。采用前文提出的数学模型可计算出不同位置、不同匝数金属性短路时的不平衡电流有效值,进而得到发生相应短路故障时监测的灵敏系数,当灵敏系数ksen≥1.2时认为监测能灵敏报警。
采用转子匝间短路故障的计算模型对二滩发电机不同匝数短路时进入单元件横差保护TA的稳态不平衡电流有效值进行计算,如表3所示(二次值,不含基波和3次谐波分量):

图7 4号机组正常运行时单元件差流实测录波波形(a)单元件差流io1;(b) 单元件差流io2Fig.7 Recorded waveforms of single element transverse differential circuit io1 in normal operation of #4 generator(a)Single element transverse differential circuit io1;(b)Single element transverse differential circuit io2

表3 不同匝数短路时进入单元件横差保护TA的稳态不平衡电流有效值(二次值)Tab. 3 The steady-state unbalance current effective value (secondary value) of single element transverse differential protection TA when short circuit with different turns
从上表可以看出,短路1匝的不平衡电流有效值已达1.11A。此时,理论上对于单匝金属性短路,Ⅰ段的监测灵敏性已经达到1.11/0.70=1.59,非常灵敏。
5 结束语
转子绕组匝间短路是大型水轮发电机经常发生的电气故障,本文基于二滩水轮发电机故障时的仿真结果,提出了基于与极对数相关的稳态不平衡电流有效值的在线监测方法,并研发了在线监测装置。灵敏性分析表明,监测装置可实现对二滩4号机组金属性短路的无死区灵敏监测。
[1] 潘伟峰,孙尔军,朱传古. 智能水电厂主设备状态监测与状态检修技术浅析 [J]. 水电与抽水蓄能,2017,3(03): 29-34,83.PAN Weifeng,SUN Erjun,ZHU Chuangu. Brief discussion on condition monitoring and condition based maintenance technology of primary equipments in smart hydropower plant [J]. Hydro and Pumped Storage,2017,3(03): 29-34,83.
[2] Tavner P J. Review of condition monitoring of rotating electrical machines[J]. IET Electric Power Applications,2008,2(4):215-247.
[3] Gao J D,Zhang L Z,Wang X H. AC machine systems[M].Beijing : Tsinghua University Press and Springer,2009.
[4] 孙宇光,郝亮亮,王祥珩. 隐极同步发电机励磁绕组匝间短路的多回路电感参数计算 [J]. 电力系统自动化,2010,34(13):55-60.SUN Yuguang, HAO Liangliang,WANG Xiangheng.Inductance calculation of the multi-loop model for inter-turn short circuits of field windings in non-salient-pole synchronous machine.Automation of Electric Power Systems,2010,34(13):55-60.
[5] 郝亮亮,孙宇光,邱阿瑞,等. 大型水轮发电机励磁绕组匝间短路的稳态故障特征分析[J]. 电力系统自动化,2011,35(4):40-45.HAO Liangliang,SUN Yuguang,QIU Arui,et al. The steadystate fault characteristics of a large hydro-generator with interturn short circuit of field windings [J]. Automation of Electric Power Systems,2011,35(4):40-45.
[6] 诸嘉惠,邱阿瑞. 转子偏心对凸极发电机主保护不平衡电流的影响 [J]. 电力系统自动化,2009,33(7): 57-60.ZHU Jianghui,QIU Arui. Effects of rotor eccentricity on unbalanced current of salient-pole synchronous generator main protection [J].Automation of Electric Power Systems. 2009,33(7):57-60 .
[7] HAO Liangliang,SUN Yuguang,QIU Arui,et al. Steadystate calculation and online monitoring of interturn short circuit of field windings in synchronous machines [J]. IEEE Transactions on Energy Conversion,2012,27(1):128-138.

