早期高空核电磁脉冲的自洽粒子模拟
付梅艳, 张茂钰
(1. 北京大学 数学科学院, 北京 100871; 2. 西北核技术研究所, 西安 710024)
早期高空核电磁脉冲(early-time high altitude electromagnetic pulse, E1-HEMP)是一种强度大、频率高、频谱宽的电磁脉冲,危害性很大[1]。20世纪60年代,Karzas和Latter讨论了其产生机理[2-3],认为在其产生过程中有一小部分核爆炸能量,经过几个中间步骤转换为射频电磁能。转换的第1步是核爆炸释放出γ射线;第2步是γ射线与大气或其他物质相互作用。事实上,高空核爆时,释放大量的瞬发γ光子(简称γ光子)。γ光子在向外辐射的过程中与周围稀薄的大气相互作用散射出康普顿电子。散射出的康普顿电子以接近光速的速度径向向外运动,形成康普顿电流。康普顿电子在向外运动的过程中,受到地磁场的作用,运动轨迹发生偏转。因此,所形成的康普顿电流除了径向分量外,还有明显的横向分量,从而激励出强电磁脉冲。同时,康普顿电子在大气中迁移时,会不断与空气发生碰撞损失能量,使空气发生电离产生次级电子-离子对。康普顿电子受到电磁脉冲场的洛伦兹力的作用,形成新的康普顿电流;次级电子-离子对受到电磁脉冲场中电场力的作用发生漂移,形成漂移电流,它将抑制场强的增长,与电磁场方程中的电导率相对应。这些电流源作为源项,激发新的电磁脉冲场。可见,E1-HEMP的产生是电磁脉冲场与康普顿电子相互作用的自洽过程。
对E1-HEMP产生过程的数值模拟,过去常采用非自洽的处理方法[4-5],即仅考虑地磁场对康普顿电子的作用,不考虑E1-HEMP对康普顿电子的影响。在一定理论分析和假设近似的基础上,用这种处理方法可以较为简单和容易地得到康普顿电流源和电导率,进而求解麦克斯韦方程获得电磁脉冲场。Karzas和Latter认为E1-HEMP对康普顿电子运动的作用发生在电流脉冲后期,只会影响E1-HEMP的时域波形,而不会显著改变发生在早期的、备受关注的峰值电场强度[3]。美国空军武器实验室在20世纪70年代曾编制过代码CHEMP[6],用来检验E1-HEMP对康普顿电子的影响,但是没有明确的结论。王建国等通过比较带电粒子受到电场力和地磁场力大小,说明了E1-HEMP对康普顿电子影响的重要性[1]。程引会等利用等效电导率的概念分析了自洽效应,结果显示考虑自洽效应可使电场强度比不考虑自洽效应得到的电场强度减小约10%[7]。
本文针对一维近似模型,采用全电磁粒子模拟方法[8-9],数值模拟了E1-HEMP产生的自洽过程,介绍了理论及计算模型,并给出了算例。
1 理论模型
1.1 麦克斯韦方程组
国际单位制下Maxwell方程组的2个旋度方程为
(1)
(2)
其中,E,B,J分别为电场强度、磁感应强度和电流密度,都是位置和时间的函数;ε0和μ0分别为真空介电常数和真空磁导率;σ为电导率。
1.2 康普顿电流
康普顿电流是由康普顿电子的运动形成的。求解康普顿电流的时空分布,需要知道康普顿电子数密度的时空分布和电子的速度。
1.2.1 康普顿电子的产生
高空核爆炸时,产生大量的γ光子。在分析γ光子在大气中辐射传输并产生康普顿电子的过程时,采取2个假设近似:1)每一个γ光子发生康普顿散射只散射出一个康普顿电子。不再考虑散射γ光子。2)γ光子与周围大气发生康普顿散射作用的概率是γ光子在当地的自由程的倒数,即γ光子在一个自由程内均匀产生出康普顿电子。
爆点处,γ光子的产生率为[5]
(3)

(4)
根据射线传输理论,在爆点产生的γ 光子将以光速c在大气中传输,且在传输过程中γ 光子强度有扩散和吸收衰减[10]。从t时刻开始,在dt时间内,到达距离爆心r处的γ 光子数dNγ(r,t)为
(5)
γ光子在r处产生的康普顿电子数dNpri(r,t)为
(6)
其中,λ(r)为γ光子在r处的自由程。
1.2.2 康普顿电子的运动
在电磁场和地磁场中,康普顿电子受牛顿-洛伦兹力的作用,速度和位置随时间发生变化。当康普顿电子的速度与光速相差不大时,其运动方程为相对论牛顿-洛伦兹力方程:
(7)
(8)
其中,m0是康普顿电子的静止质量;v是康普顿电子的速度;γ是相对论因子;B0是地磁场的磁感应强度。
1.2.3 康普顿电子的消失
康普顿电子在大气中迁移与周围空气分子、原子不断发生碰撞,损失能量。类似γ光子的吸收衰减,康普顿电子数按指数规律衰减:
(9)
其中,L1是康普顿电子开始衰减的位置,即产生的位置;N1是在L1处的康普顿电子数;L2是考察点位置;N2是在L2处的康普顿电子数;Re(r)是康普顿电子在r处的最大射程。
1.3 电导率
康普顿电子与大气分子碰撞时,损失自身能量的同时使空气分子发生电离,产生大量的次级电子和正离子。康普顿电子平均损失能量33 eV,可产生一对次级电子和离子。次级电子和离子的贡献是使空气的电导率σ大大增加。σ可以通过求解空气化学方程得到[4],也可通过分析等离子体参数得到[11],计算公式为
(10)
其中,nsec(t)表示二次电子的数密度;eq表示二次电子电荷的绝对值;msec表示二次电子的静止质量;υ为二次电子的碰撞频率。
类似于γ光子产生康普顿电子的过程,假设二次电子由康普顿电子在一个射程内均匀产生,可得到二次电子。t时刻,在r处康普顿电子产生二次电子的速率为
(11)
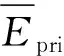
2 计算模型
2.1 宏粒子模型
宏粒子是全电磁粒子模拟方法中的基本概念之一,是指由相空间中一些带电粒子形成的、具有一定形状和空间分布的“超级粒子”。宏粒子中所有电子的速度相同。假设宏粒子包含n个带电粒子,则宏粒子的电荷为ne,质量为nm,其中,e为电子的电荷,m为电子的质量。这里,带电粒子是指康普顿电子。
按照一定的标准,把每一时刻、每个空间位置处新产生的康普顿电子设置为一定数目的宏粒子数。例如,将100个康普顿电子视为一个宏粒子。对计算区域内所有宏粒子的位置、速度及包含的康普顿电子数进行叠加,即可得到它们产生的初级电流密度。同时,设置一定的阈值,当宏粒子所包含的康普顿电子数小于该阈值时,则认为宏粒子已经衰减殆尽。
2.2 电磁场方程的计算
将式(1)、式(2)在球坐标系下展开,略去θ、φ的偏微商项,三维问题可以简化为一维问题[5],得到电磁场方程为
(12)
(13)
(14)
(15)
(16)
(17)
采用时域有限差分方法求解上述方程,取Mur一阶近似边界条件,右边界条件为
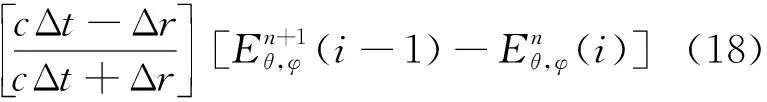
左边界条件为
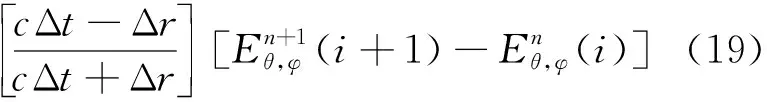
2.3 相对论牛顿-洛伦兹力方程的求解
采用Boris提出的“半加速-旋转-半加速”方法中的修正公式,求解相对论牛顿-洛伦兹力方程,可得到宏粒子的速度和位置[12]。
2.4 电流密度和电磁场量的分配
为了避免“自力”的产生,电流的分配方法和电磁场量的分配方法一致。本文采用Eastwood提出的方法[13],即根据宏粒子运动的起点和终点,计算电流流量,如果宏粒子的运动超过一个网格,则把整个运动分解成一系列网格内的运动,然后,把每一网格内的电流密度分配到网格线上。对所有宏粒子都以同样的方式进行处理。
3 算例
3.1 计算条件
选取爆高为100 km,当量1 000 kt。假设1 kt当量产生的能量为2.61×1025MeV,爆炸当量的0.3%以能量为1.5 MeV的瞬发γ光子释放。瞬发γ源的时间变化函数取双指数函数,相应参数分别为4.0×107s-1和4.76×108s-1。康普顿电子的初速度为v=(vr,vθ,vφ)=(βc, 0, 0), 其中,常数β=0.914,c为光速。地磁场的简化近似及坐标系的选取方法与文献[14]一致。
一维计算区域的方向位于距离爆心投影点正南约170 km处的点与爆心之间的连线方向;计算范围为rbegin≤r≤rend,其中rbegin为计算区域内半径,rend为计算区域外半径。这里取rbegin为69.282 km,rend为92.376 km,对应的高度范围hbegin为40 km,hend为20 km。空间网格步长dr取0.5 m,时间步长取1.0×10-10s,满足Courant-Friedrich-Levy条件的要求。给出了三个观测点P1,P2,P3上的计算结果,它们距离计算区域内半径分别为50, 500, 1 000 m。计算区域及观测点在整个空间的位置和方向示意图,如图1所示,图中粗线部分即为计算区域。
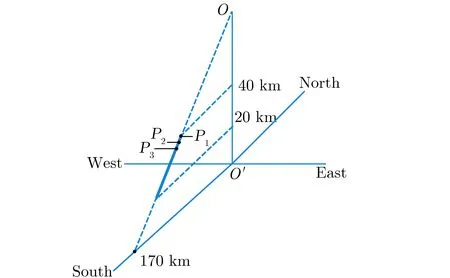
图1 计算区域示意图Fig.1 Diagram of computational region
3.2 计算结果
图2—图10为P1,P2,P3处电场分量的时域波形图,并与非自洽处理方法的计算结果进行了比对。
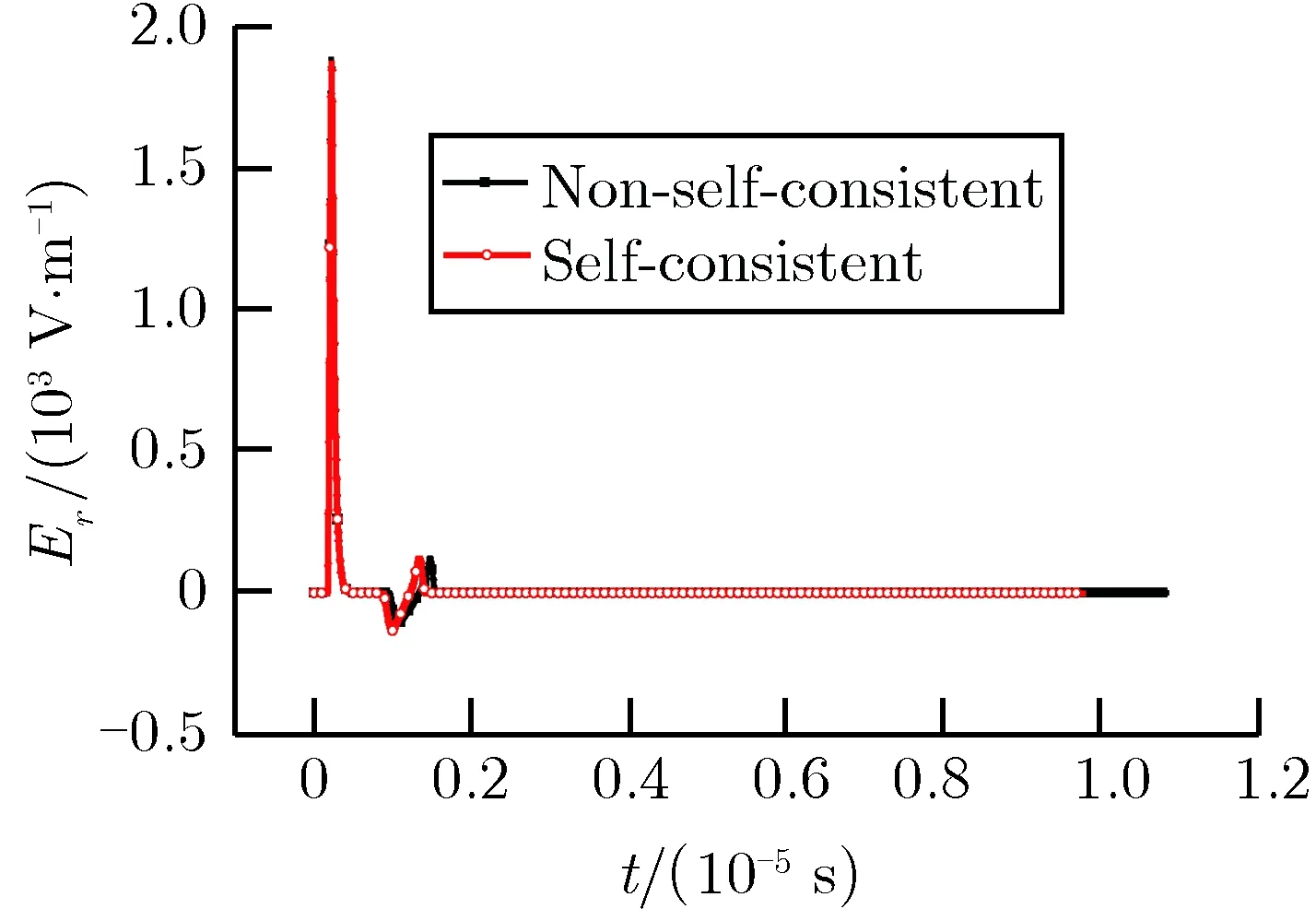
图2 观测点P1的Er时域波形Fig.2 Waveform of Er at test point P1
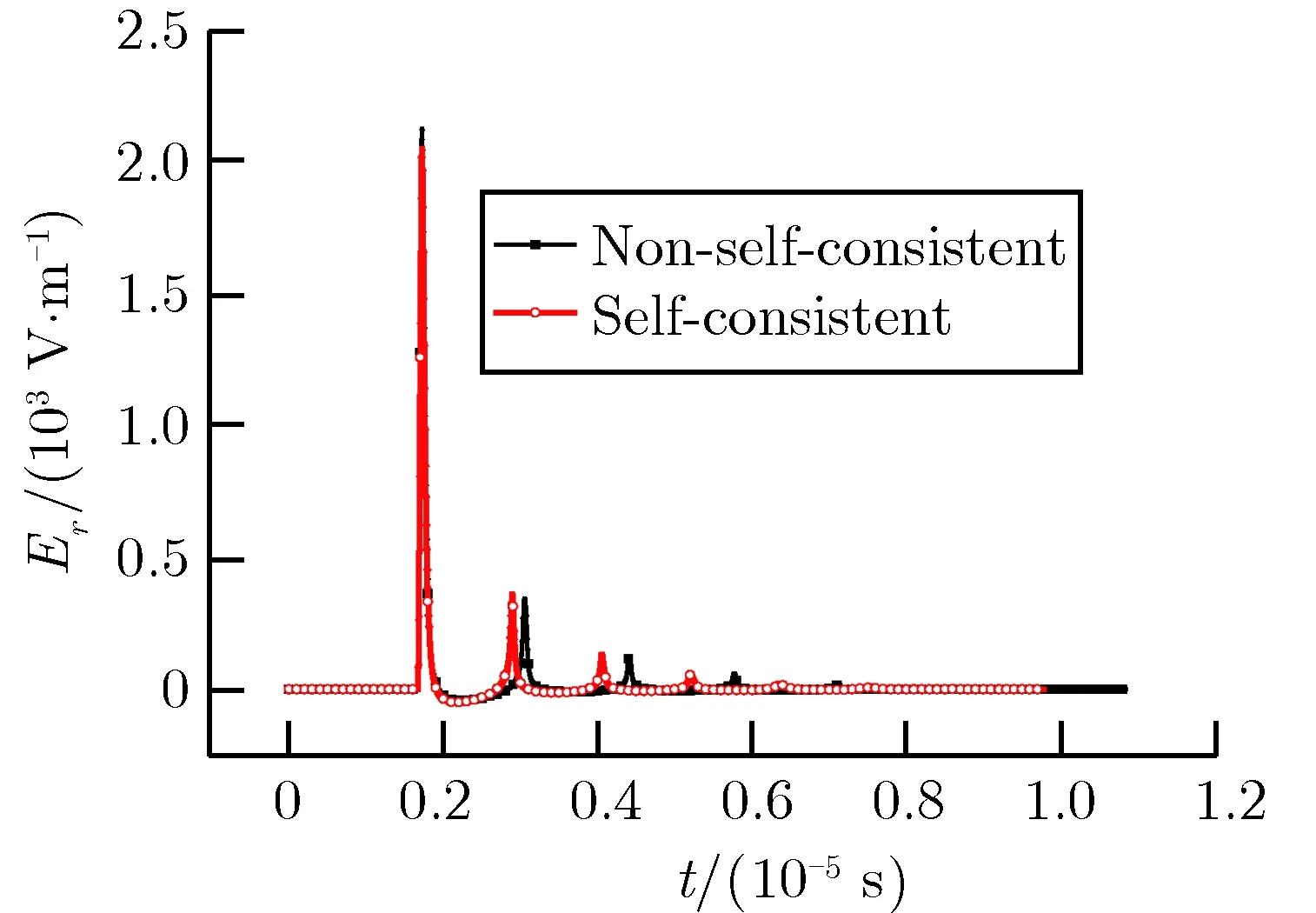
图3 观测点P2的Er时域波形Fig.3 Waveform of Er at test point P2
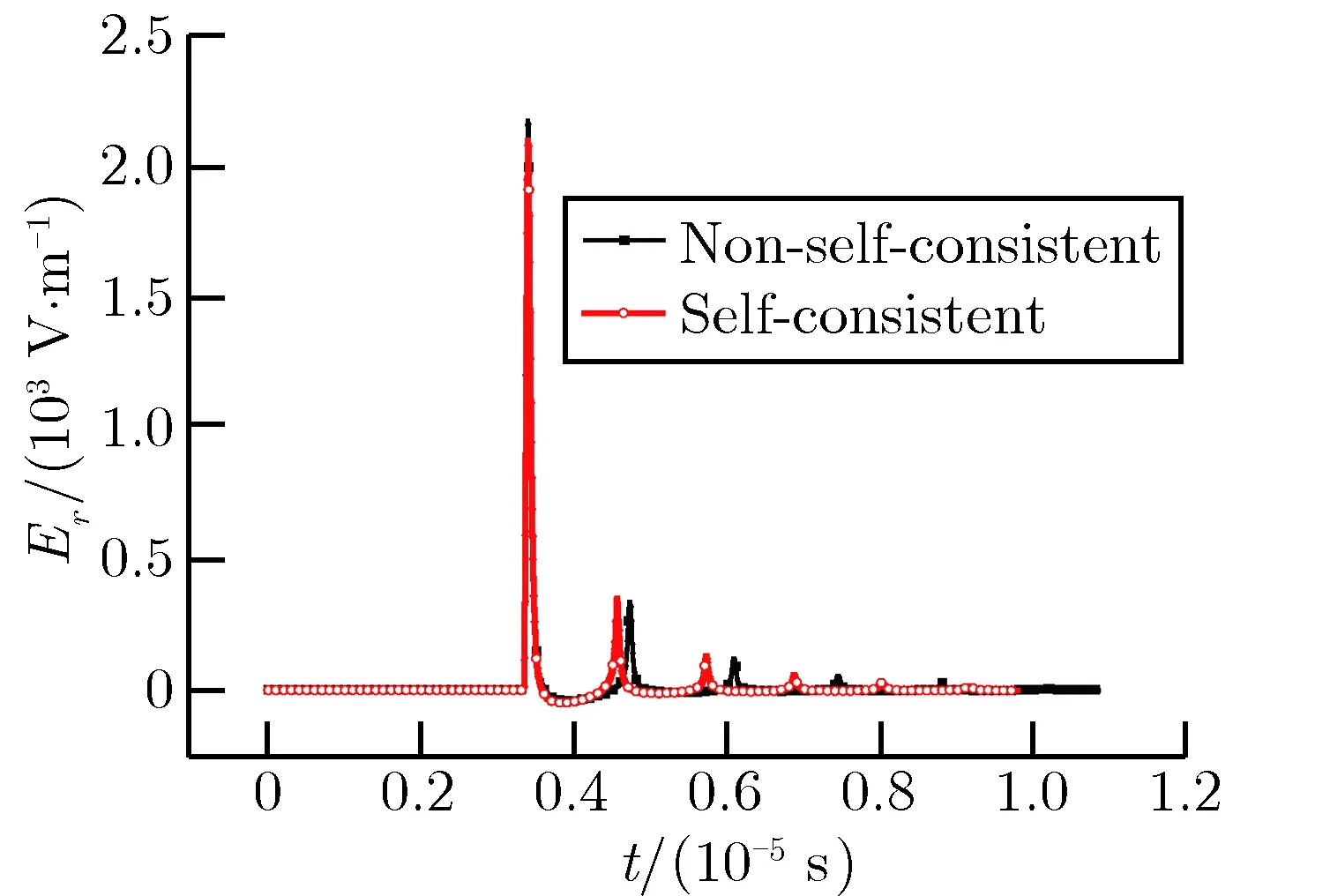
图4 观测点P3的Er时域波形Fig.4 Waveform of Er at test point P3

图5 观测点P1的Eθ时域波形Fig.5 Waveform of Eθ at test point P1

图6 观测点P2的Eθ时域波形Fig.6 Waveform of Eθ at test point P2
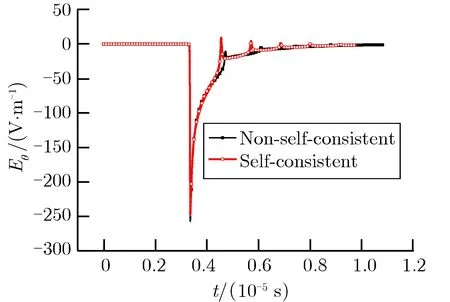
图7 观测点P3的Eθ时域波形Fig.7 Waveform of Eθ at test point P3

图8 观测点P1上的Eφ时域波形图Fig.8 Waveform of Eφ at test point P1
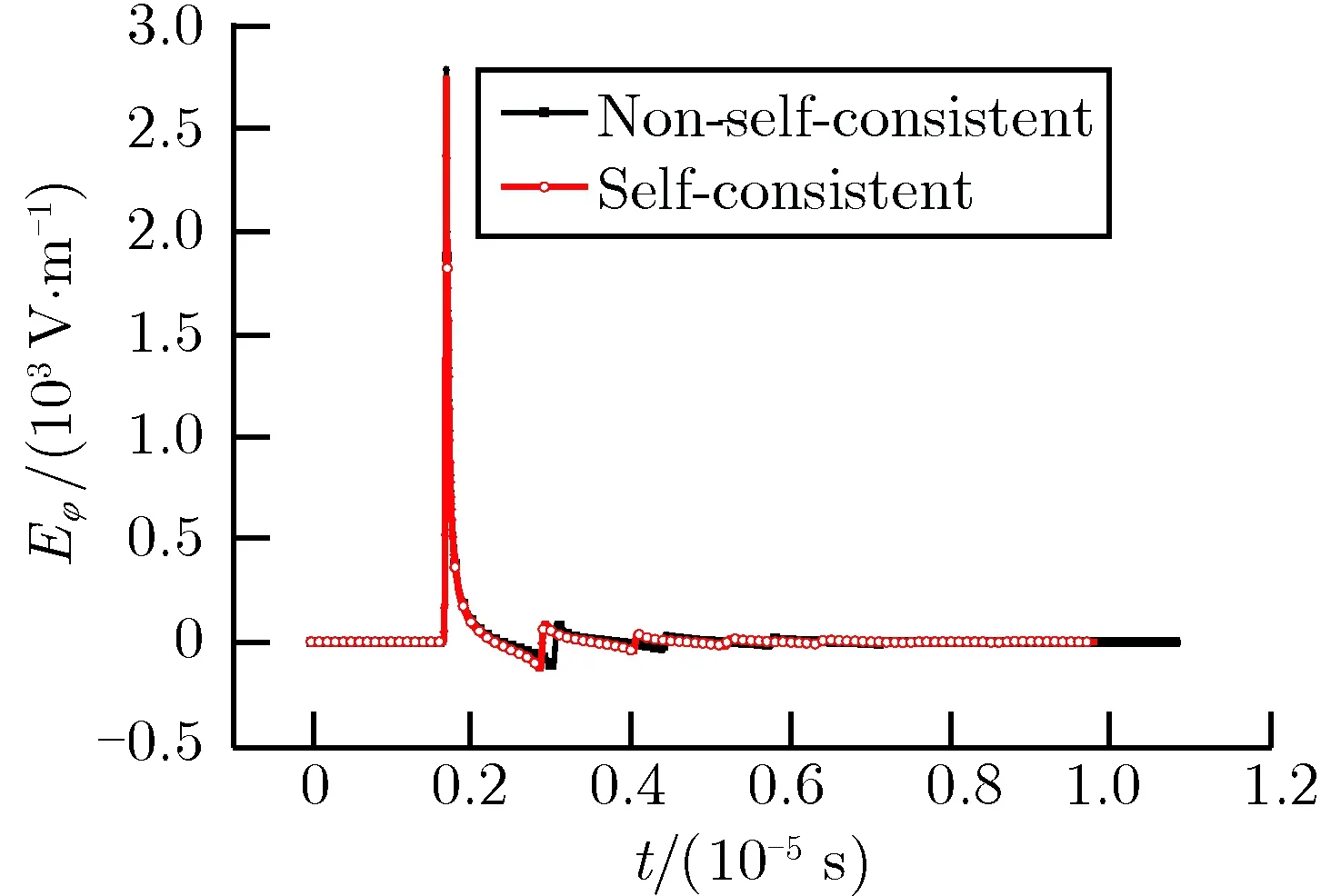
图9 观测点P2的Eφ时域波形Fig.9 Waveform of Eφ at test point P2
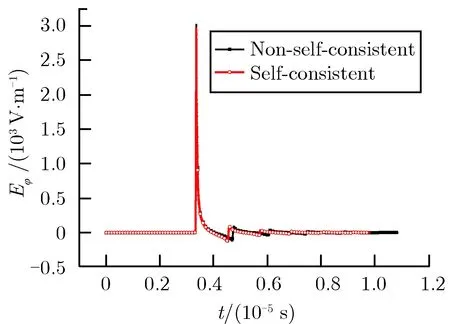
图10 观测点P3的Eφ时域波形Fig.10 Waveform of Eφ at test point P3
从图中可以看出,用自洽处理方法计算出来的电场时域波形和用非自洽处理方法计算出来的电场时域波形整体形状几乎一致,到达第1峰值电场强度的时间几乎相同,差别在于:1)用自洽处理方法计算出来的第1峰值电场强度小于非自洽处理方法的计算结果,但两种方法计算的第2、第3峰值电场强度结果相当; 2)用自洽处理方法计算出来的第1峰值电场与第2峰值电场之间的时间间隔小于用非自洽处理方法计算出来的量,会使第1波峰电场与第2峰值电场之间的时间间隔缩短。但从第2波峰往后的波峰和波峰之间的时间间隔,两种方法的计算结果几乎相同。
4 讨论
本文采用全电磁粒子模拟方法和一维近似模型,数值模拟了电磁脉冲场与康普顿电子相互作用产生E1-HEMP的过程。从源区场的计算结果可知,考虑自洽效应计算出来的第1峰值电场强度会略微减小,到达第2、第3等峰值电场强度的时间变快了,波形形状发生了改变,这和Karzas等对自洽作用的估计[3]基本一致。
关注E1-HEMP,很多时候是关心它在地面上的时空分布,而要想得到地面上的辐射场,就需要知道到达源区下边界处的辐射场[11]。E1-HEMP的源区高度范围达20~30 km,而全电磁粒子模拟方法中计算电磁场的FDTD方法对网格步长、时间步长有严格的限制,再加上对宏粒子的处理非常费时,所以在有限时间内,只能得到少数几个观察点上的电场时域波形,无法得到整个源区内辐射场的时空分布,进而无法得到源区外辐射场的时域变化。下一步,拟在推迟时间变换下,进一步研究E1-HEMP产生的自洽过程。
[1]王建国, 牛胜利, 张殿辉, 等. 高空核爆炸效应参数手册[M]. 北京: 原子能出版社, 2010: 145-148. (WANG Jian-guo, NIU Sheng-li, ZHANG Dian-hui, et al. Parameter Handbook of High Altitude Nuclear Detonation Effects [M]. Beijing: Atomic Energy Press, 2010: 145-148.)
[2]KARZAS W J, LATTER R. Electromagnetic radiation from a nuclear explosion in space [J]. Phys Rev, 1962, 126(6): 1 919-1 962.
[3]KARZAS W J, LATTER R. Detection of the electromagnetic radiation from nuclear explosions in space [J]. Phys Rev, 1963, 137(5B): 1 369-1 378.
[4]LONGMIRE C L. On the electromagnetic pulse produced by nuclear explosions [J]. IEEE Trans Antennas Propag, 1978, 26(1): 3-13.
[5]陈雨生. 核爆炸电磁脉冲研究[C]// 核爆电磁脉冲技术交流会文集, 北京: 国防科工委情报资料研究所, 1980: 1-35. (CHEN Yu-sheng. Research on NEMP technical communion conference corpus on NEMP[C]// Beijing: National Deference Scientific and Engineer Committee, 1980: 1-35.)
[6]WITTER L A, CANAVAN G H, BRAV J E. CHEMP: A code for calculation of high-altitude EMP[R]. AD-783239, Air force Weapons Lab., 1974.
[7]程引会, 李进玺, 马良, 等. 高空电磁脉冲环境计算中的自洽方法[J]. 计算物理, 2017, 34(4): 403-408. (CHENG Yin-hui, LI Jin-xi, MA Liang, et al. Self-consistent method in calculation of high-altitude electromagnetic pulse environment [J]. Chinese Journal of Computational Physics, 2017, 34(4): 403-408.)
[8]DAWSON J M. Particle simulation of plasmas [J]. Review of Modern Physics, 1983, 55(2): 403-447.
[9] BIRDSAL C K, LANGDON A B. Plasma Physics via Computer Simulation [M]. New York: Adam Hilger, 1991: 55-79.
[10] BYRD R L. Atmospheric transport of neutrons and gamma rays from a high-altitude nuclear detonation[R]. LA-12962-MS. Los Alamos National Laboratory, 1995.
[11] MENG C. Numerical simulation of HEMP environment [J]. IEEE Trans Electromagn Compat, 2013, 55(3): 440-455.
[12] 王建国. 真空电子器件的粒子模拟方法[J]. 现代应用物理, 2013, 4(3): 251-262. (WANG Jian-guo. Particle simulation method of vacuum electronic devices[J]. Modern Applied Physics, 2013, 4(3): 251-262.)
[13] EASTWOOD J W. The virtual particle electromagnetic particle-mesh method[J]. Computer Physics Communications, 1991, 64(2): 252-266.
[14] 付梅艳, 张茂钰. 用高频近似模型和入射-出射波模型对早期高空核电磁脉冲场的计算比对[J]. 现代应用物理, 2015, 6(2): 107-112. (FU Mei-yan, ZHANG Mao-yu. Comparison of two simplified model of early-time high altitude electromagnetic pulse field equation [J]. Modern Applied Physics, 2015, 6(2): 107-112.)

