Case study on wave-current interaction and its effects on ship navigation *
Chen Chen
JSPS Researcher, Department of Naval Architecture and Ocean Engineering, Osaka University, Suita, Osaka,Japan
Introduction
Wave-current interaction (WCI) has become an issue of increasing interest as the growing scale of large offshore and coastal structures such as offshore platforms, wave energy facilities as well as wind turbines. Extreme loading on those structures is generally coming from the combination effects of waves and currents. Significant currents such as many tidal currents and large ocean circulations can be of great importance for ship routing considering the navigation economy of both time and fuel consumptions[1-2]. Moreover, such currents can also affect ship safety when they encounter with ocean waves. The existence of a current can change wave celerity, which can then affect the wave length and observed wave period. Moreover, in addition to the change of wave speed and length, the wave height will also change when a wave travels from one current region to another one, where wave breaking may occur.Especially, such strong boundary ocean current can generate strong horizontal shear, leading to refraction of the waves and focusing of wave energy when waves run opposite the current direction.
As a problem of wave propagation in an inhomogeneous dispersive, dissipative and moving medium,WCI have been studied by many researchers concerning linear and regular waves on currents. As the first study, the concept of radiation stress by the correct energy equation as well as the existence of the energy transfer between waves and currents has been proved by Longuet-Higgins and Stewart[3-4]. Then, a conservation equation for wave action valid for waves travelling on a slowly varying current was given by Bretherton and Garrett[5]. Dissipation and diffraction problems were then introduced into the wave conservation equation by Christoffersen and Jonsson[6]as well as Booij[7]and Kirby[8], respectively.
In addition to the observations[9]and experimental studies[10-12]of WCI, with the development of modernized 3rd generation wave models, such as the Simulating Waves Nearshore (SWAN) model[13],numerical studies of ocean waves as well as WCIs have become possible. By using a 3-D wave–current coupled modeling system based on Princeton Ocean Model (POM)[14]and SWAN, Xie et al.[15]studied the effects of WCI on the storm surge and inundation induced by Hurricane Hugo in and around the Charleston Harbor and its adjacent coastal regions.Benetazzo et al.[16]investigated the effect on waves of the WCI process in the semi-enclosed Gulf of Venice using the coupled ROMS[17]and SWAN. Other studies on WCI at estuaries where relatively strong currents exist by using SWAN can be found in Refs. [18-19].
Other studies on the wave Interaction with strong boundary ocean current have also been done.Tolman[20]showed that the wave height was increased for waves traveling against the Gulf Stream and currents had a distinct effect on the wave spectrum.Additionally, Anderson et al.[21]has demonstrated the impact of the meandering Kuroshio Current with a 1/32° resolution wave model coupled to the ocean model ocean circulation and climate advanced modelling project (OCCAM).
As an extension of my past study on the effects of the Kuroshio Current on ship navigation[2], which has mainly taken the economical aspect into consideration, the present study will focus on the influence of ocean current upon waves in the Kuroshio Current region as well as its influences on ship navigation, by using high resolution wave model SWAN and precalculated wind and current by WRF and POM,respectively[22].
1. Wave model
As a numerical model for simulating waves,SWAN, a third-generation wave simulation model developed at Delft University of Technology was applied here to simulate waves affected by the low pressures. Implemented with the wave spectrum method, it is a third-generation wave model that can compute random, short-crested, wind-generated waves in coastal regions as well as inland waters. The SWAN model is used to solve the spectral action balance equation without any prior restriction on the spectrum for the effects of spatial propagation,refraction, reflection, shoaling, generation, dissipation,and nonlinear wave-wave interaction. Because in the presence of currents, the action density is conserved instead of the energy density, the SWAN uses the action density spectrum, rather than the energy density spectrum.
A typhoon with intense and fast-varying winds forms a complex ocean wave field which can propagate thousands of kilometers away from the storm center, resulting in dramatic variation of the wave field in space and time. Waves under typhoon wind were simulated successfully by SWAN wave model[23].As a very important way, ocean wave modeling is a very useful and convenient way to obtain the spatial and temporal distribution of directional spectra without the limitations associated with measurements.
Consequently, the SWAN model is suitable for estimating waves in bay areas with shallow water and ambient currents. Information about the sea surface is contained in the wave variance spectrum of energy density (,)Eσ θ . Wave energy is distributed over
frequencies ()θ and propagation directions ()σ. σ is observed in a frame of reference moving with the current velocity, and θ is the direction normal to the wave crest of each spectral component. The expressions for these propagation speeds are taken from linear wave theory, while diffraction is not considered in the model. The action balance equation of the SWAN model in Cartesian coordinates is as follows

where the right-hand side containsS, which is the source/sink term that represents all physical processes that generate, dissipate, or redistribute wave energy.The equation ofSis as follows
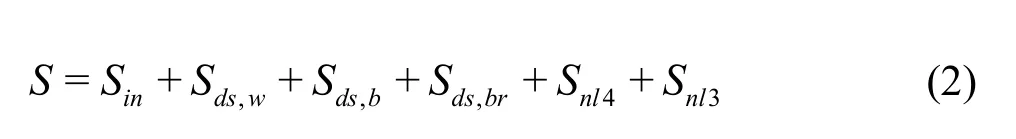
whereinSis the term for transferring of wind energy to the waves[24],,ds wSis the term for the energy of whitecapping,,ds bSis the term for the energy of bottom friction and,ds brSis the term for the energy of depth-induced breaking. In deep water, the three parts wind energyinS, energy of whitecapping,ds wSand nonlinear quadruplet interaction4nlSare important, while in shallow water, other parts bottom friction,ds bS, depth-induced wave breaking,ds brSand triad nonlinear wave-wave interaction3nlScan play an important role. According to Janseen[25], for real ocean waves, besides the four-wave Interaction determine the evolution of the spectrum of surface gravity waves, wind input and dissipation due to white-capping are also relevant, and together, these processes may affect the kurtosis of the sea surface as well.
Because of energy bunching, current induced refraction, energy transfer between waves and currents as well as frequency shifting; wave height, wave period and wave frequency may change when waves encounter a varying current. If we assume the current is moving with the velocity (,)tU x , the frequency of wave system passing a certain fi eld point can be shifted by the Doppler Effect, according to Rusu and Guedes Soares[18], shown as follows

where ω and σ are absolute and relative wave frequency, respectively. Therefore, the (Eq. (1)) can be written as
where θ is the wave direction,gC,CδandCθare the propagation velocities of the wave energy in physical and spectral space, respectively. The left side of Eq. (4) are the kinematic part. The first term expresses the change rate of the wave action density,the second term is the effect of shifting of the radian frequency due to variations in depth and mean currents, and the third term represents refraction effects caused by depth- and currents. The last term represents the propagation of wave energy in 2-D geographical space. The right side of the equation has the same meaning with that shown as Eq. (2).


Fig. 1 (Color online) 10 m wind velocity distributions from WRF model, 28th May, 2011, 00:00 UTC
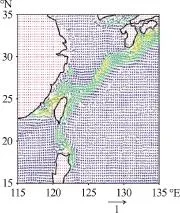
Fig. 2 (Color online) Averaged ocean surface current vector distribution of the calculation area by POM, for 1992-2012[2]
2. Numerical simulations of WCI
the effects of WCI into consideration. To continue the previous study, WCI are calculated here using the wave model SWAN. For wind calculation input to SWAN, a representative typhoon (SONGDA) observed in the East China Sea was selected for the WRF calculation[3], with a horizontal resolution of 0.5°×0.5°,vertical level number of 28 as well as simulated time of 120 h from 25th May, 2011, 00:00 UTC to 31th May, 2011, 00:00 UTC see Fig. 1.
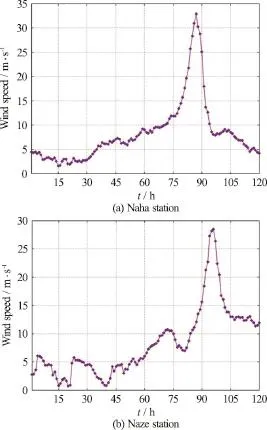
Fig. 3 (Color online) Wind speed generated by WRF
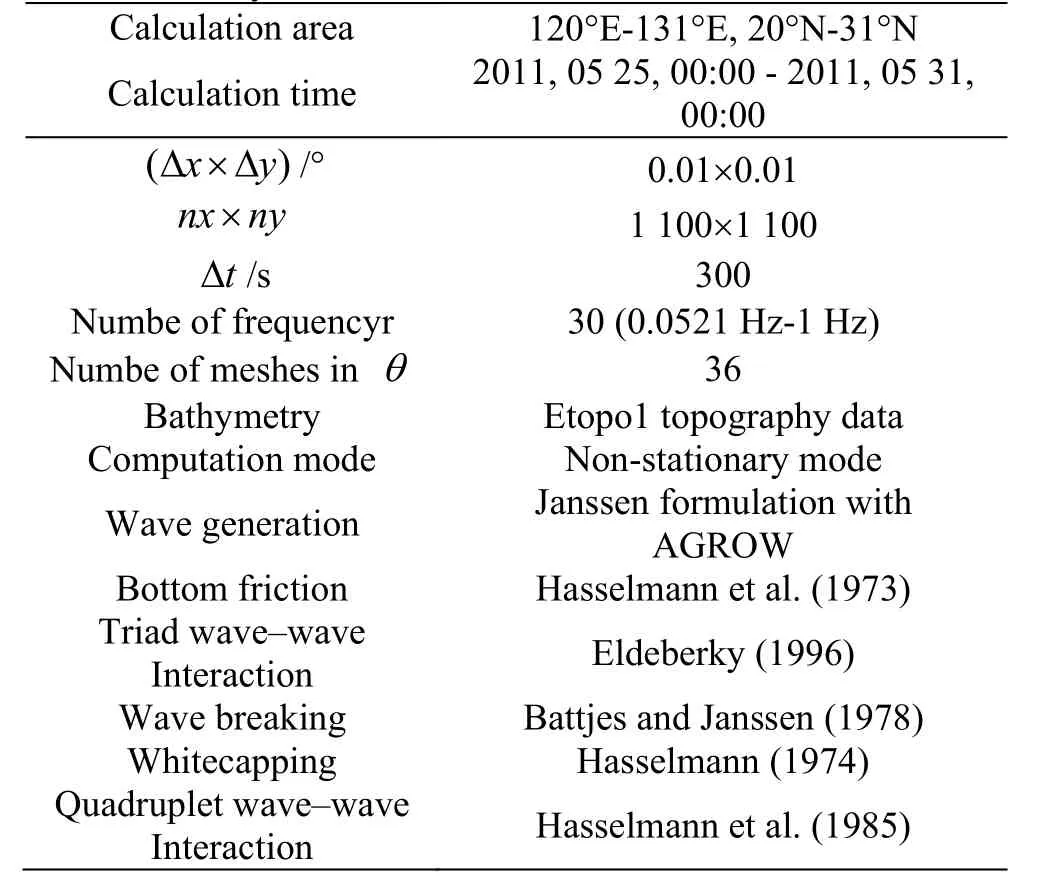
Table 1 Grid settings and physics options of wave calculation by the SWAN model
The previous study[2]has quantitatively figured out the influence of the Kuroshio Current on ship navigation in the economical aspect, without taking

Fig. 4 (Color online) Comparisons of SWH, AWP and MWD between SWAN (with, blue line and without current, green line)cases and NOWPHAS (purple line) in the above-mentioned two stations
For current input data, the previous POM result is used. The horizontal coordinate used here is the Mercator, with a horizontal resolution of 0.1°×0.1°, 30 sigma vertical coordinates with a finer resolution in the upper layers are adopted. The time mean ocean surface current data is used, as shown in Fig. 2. Cubic spline data interpolation method was used to generate appropriate wind and current fields to match the spatial and temporal resolution of SWAN.
Two different calculations were done with the SWAN model, with and without current input,respectively. For both of them, the SWAN model was set to a horizontal resolution of 0.01°×0.01°. The minimum water depth in the model is 10 m and the time step is 5 min. The wave spectrum is discretized using 36 directions (=10)θΔ and 30 frequencies extending from 0.0521 Hz to 1 Hz with a logarithmic increment. Table 1 gives the detailed grid settings and physics options of wave calculations.
Wave information of every 2 h at two observation stations: Naha (127°41′1″E, 26°12′4″N) and Naze (129° 31′18″E, 28°27′07″N) from NOWPHAS,where the interaction between waves and currents may induce relatively significant variations, are used for model validation. The time 2011, 05 28, 15:00 and 2011, 05 29, 00:00 were selected for Naha and Naze,respectively; because of the highest wind speed distribution at those time, according to Fig. 3, which shows wind speed generated by WRF in Naha and Naze stations.
The comparisons of SWH, AWP and MWD between SWAN (with, blue line and without current,green line) and NOWPHAS purple line in the above-mentioned two stations are shown in Fig. 4.Larger SWH can be found in the case of with current than without current, and the reason can be the opposite directions of wave and current at those time and locations, see Fig. 5.
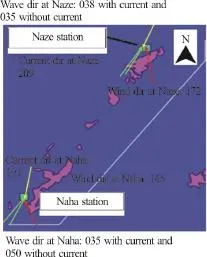
Fig. 5 (Color online) Locations of two NOWPHAS buoys, both at western side to the islands, with calculated directions of wind, wave and current at the time of 2011, 05 28,15:00 and 2011 05 29 00:00 for Naha and Naze, respectively
Relatively lower AWP were calculated by SWAN, when compared with the NOWPHAS data,which may result from the following two reasons:firstly, the underestimation of SWAN model due to the relatively course resolution in time and space of the WRF wind calculation, because the Tm02 is rather sensitive to errors in the wind forcing and as it does not really represent the energy containing part of the spectrum, secondly: the less exposed locations of buoys, see Fig. 5, the measurements at the buoys were located in the western area of Naha island and the influence of the island plays a significant role on the definition of the wave field when the dominant winds are from the east, as shown in the period before 80 h in Fig. 3 and in the period before 40 regardless of direction and period terms in the Fig. 4, in which period the low-frequency swell is the dominate sea states, for which the SWAN model tends to underestimate the wave spectra[26]. However, obvious differences have been shown between with and without current cases, especially for the high winds, which shows that wave-current interaction can have an influence on the reduction of wave periods in the present calculation cases.
While for wave directions, the SWAN results are 035 degree (with current), 050 degree (without current)in the Naha and 038 degree (with current), 036 degree(without current) in the Naze station at the time of 2011, 0528, 15:00 and 2011, 0529, 00:00, respectively.Good agreements have been achieved for direction calculation, especially for the high wind time period,as shown in the period between 60 h and 80 h in Fig. 3 and in the period from 30 to 40 regardless of direction terms in the Fig. 4, where results from similar reason as mentioned for AWP.
Finally, Fig. 4 can also show that AWP is more sensitive to the existence of currents than SWH, while relatively small differences may be found between two cases regardless of MWD although the calculation result is slightly better in case of with current.
Considering the direction of the main path of Kuroshio Current, two wave directions of 045 and 225(forced by wind stress, 5 m/s, 10 m above sea surface)have been studied the opposite and following currents,respectively, by which a better understanding of the WCI is expected. Additionally, Benjamin–Feir instability (BFI), directional spreading (DS) as well as wave length (WL) are compared between cases of wave-with-current (W-C) and wave-without-current(W-O-C) in the whole calculated ocean area, see Fig.6.
It can be clearly observed that, due to waves got Doppler shifted, following current (Case 045) has an effect on decrease of SWH and BFI, while increase of AWP and WLEN. While in case of 225, opposite current increases SWH and BFI, while decreases AWP and WLEN. Waves tend to turn to the right side due to the current refraction. Current-induced refraction can also be found trough the figure of MWD. And we also considered the effect of the WCI on the wave directional spreading, as this is an important variable for the stability of the wave train in deep water and for its evolution[28]. We can find that the presence of the currents modifies considerably the spectral shape especially by spreading the wave energy towards the high frequency domain.
3. Influences of WCI on ship navigation
Variations in the wave parameters, such as wave height, wave period and wave direction, due to currents is a problem of great importance in various engineering applications, especially in the aspect of reduce the navigational risk. Moreover, WCI has been also proposed as a possible mechanism for the formation of giant waves, such as rogue waves (also known as freak waves, monster waves, episodic waves,killer waves, extreme waves, and abnormal waves),which are large, unexpected and suddenly appearing surface waves that can be extremely dangerous, even to large ships such as ocean liners. When a wave group encounters an opposing current, such as the strong boundary ocean currents, the waves in the group may pile up on top of each other which will pro-pagate into a rogue wave, which an impact with a much larger breaking force than designed limitation of modern ships, leading to serve ship accidents.
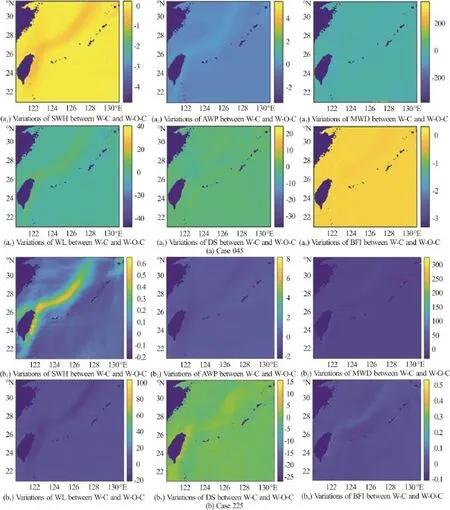
Fig. 6 (Color online) WCI for wave directions
Although it is difficult to collect hard evidence on such extreme wave phenomena because of the low possibility of their occurrence, observational evidence suggest that in case of large surface elevations, the probability distribution for the surface elevation deviates substantially from the Gaussian distribution[27].
To determine the probability of extreme events and understand the occurrence of rogue waves, the kurtosis of the surface elevation probability distribution has shown mostly determined well by the square of BFI value[28], even for waves with a narrow banded spectrum and large steepness, where a significant amount of wave breaking, limiting the height of these waves, as well as affecting the extreme statistics.
According to Janseen[25], the BFI can be defined as follows

whereStrepresents wave steepness andpQis a quantity decided by the elevation of the spectral peak
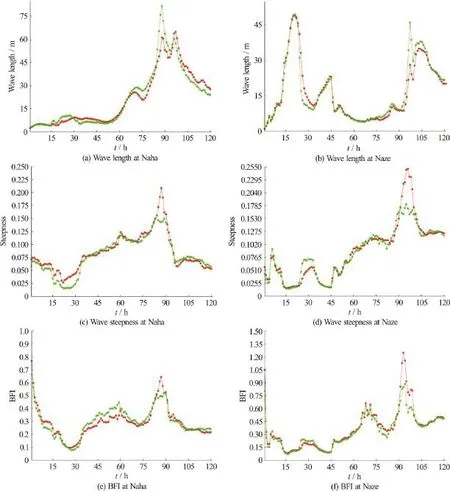
Fig. 7 (Color online) Comparisons of wave length, wave steepness and BFI value between with (red line) and without current(green line) cases at Naha and Naze stations, respectively
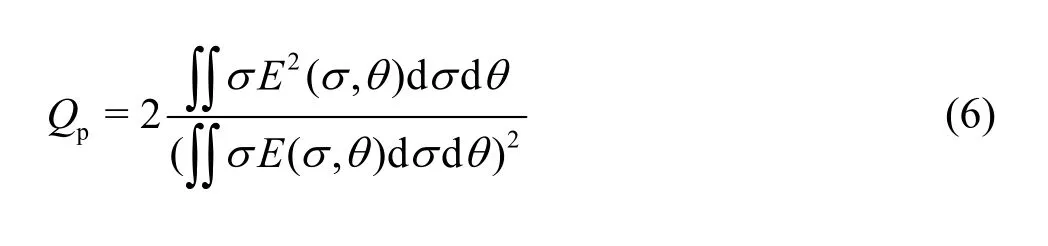
As shown in Fig. 7, results of SWAN calculations regardless of wave length, wave steepness and BFI value are compared between with (red line) and without current (green line) cases at Naha and Naze stations, respectively. Wave length is an important parameter for ship safety, many ship accidents happen when the wavelength was systematically above half the ship, as shown by Toffolia[29]. Attention should also be paid to the wave steepness, a parameter that points at an enhancement of risk of extreme waves. Steeper sea states might yield dangerous dynamic effects due to ship motion (e.g., slamming), even though the SWH is not particularly large.
Finally, it can be easily found from those comparison results that the opposite current can produce a decrease of wave length, increase of wave steepness and BFI value, which shows that ship navigation may encounter a higher risk because of the high possibility of extreme wave occurrences in fully developed seas.
4. Conclusions
As an continuous study to my previous study on the economic effects of the Kuroshio Current on ship navigation, to quantitatively figure out the WCI as well as its influences on the ship safety in the Kuroshio Current region, several high-resolution wave model calculations have been done in the present study, considering two cases: with current and without current.
WRF and POM model provide the input information of ocean surface wind and current to the wave model SWAN, which run at a relatively high resolution. Important wave parameters that can describe the short term wave statistics, such as SWH, AWP as well as MWD calculated by wave model SWAN were verified by NOWPHAS observation data at two stations. Additionally, together with SWH, AWP as well as MWD, wave length (WLEN), BFI, frequency and directional spreading are also compared between cases of W-C and W-O-C in the whole calculated ocean area.
Owing to the WCI, obvious differences of those short term wave characteristics can be found between with and without current cases, which in turn can illustrate the influence of the strong western boundary ocean current on wave prorogations. Current moving at opposite direction with wave can have an effect on increase SWH and AWP, while the effects on AWP are larger than that on SWH. In case of the influences on MWD, there are not obvious differences according to the model results.
For the ship navigational safety consideration,other important wave parameters such as wave length,wave steepness as well as BFI value have also been calculated. Effects of WCI on these wave qualities are significant, which can increase the risk of ship accidents. It is subjected to a very high risk of strong wave occurrences not only from the point of view of the significant wave height but also with maximum heights much greater than those resulting from the standard Rayleigh distribution.
Although the present study can give an overview of the WCI, further validations from additional measurements as well as higher-resolution wind and current information are necessary to improve the wave model performance.
Acknowledgement
This work was supported by the JSPS KAKENHI(Grant No. JP16J04357).
[1] Chen C., Shiotani S., Sasa K. Numerical ship navigation based on weather and ocean simulation [J].Ocean Engineering, 2013, 69: 44-53.
[2] Chen C., Shiotani S., Sasa K. Effect of ocean currents on ship navigation in the East China Sea [J].Ocean Engineering, 2015, 104: 283-293.
[3] Longuet-Higgins M. S., Stewart R. W. Changes in the form of short gravity waves on long waves and tidal currents [J].Journal of Fluid Mechanics, 1960, 8: 565-583.
[4] Longuet-Higgins M. S., Stewart R. W. Radiation stresses in water waves, a physical discussion, with applications[J].Deep-Sea Research and Oceanographic Abstracts,1964, 11(4): 529-562.
[5] Bretherton F. P., Garrett C. J. R. Wavetrains in inhomogeneous moving media [J].Proceedings of the Royal Society of London. Series A, Mathematical and Physical Sciences, 1968, 302(1471): 529-554.
[6] Christoffersen J. B., Jonsson I. G. A note on wave action conservation in a dissipative current wave motion [J].Applied Ocean Research, 1980, 2(4): 179-182.
[7] Booij N. Gravity waves on water with non-uniform depth and current [D]. Doctoral Thesis, Delft, The Netherlands:Technische Hogeschool, 1981.
[8] Kirby J. T. A note on linear surface wave–current interaction over slowly varying topography [J].Journal of Geophysical Research Oceans, 1984, 89(C1): 745-747.
[9] Wolf J., Prandle D. Some observations of wave–current interaction [J].Coastal Engineering, 1999, 37(3-4):471-485.
[10] Thomas G. P. Wave–current interaction: An experimental and numerical study, Part 1: Linear waves [J].Journal of Fluid Mechanics, 1981, 110: 457-474.
[11] Guedes Soares C., Rodriguez G. R., Cavaco P. et al. Experimental study on the interaction of wave spectra and currents [D].Proceedings of the ETCE/OMAE Joint Conference Energy for the New Millennium,New Orleans,Louisiana, USA, 2000.
[12] Soares C. G., Pablo H. D. Experimental study of the transformation of wave spectra by a uniform current [J].Ocean Engineering, 2006, 33(3-4): 293-310.
[13] Booij N., Ris R. C., Holthuijsen L. H. A third-generation wave model for coastal regions: 1. Model description and validation [J].Journal of Geophysical Research Oceans,1999, 104(C4): 7649-7666.
[14] Mellor G. L. Users guide for a three-dimensional, primitive equation, numerical ocean model [M]. Princeton,USA: Princeton University, 2004.
[15] Xie L., Liu H., Peng M. The effect of wave–current interactions on the storm surge and inundation in Charleston Harbor during Hurricane Hugo 1989 [J].Ocean Modelling,2008, 20(3): 252-269.
[16] Benetazzo A., Camiel S., Sclavo M. et al. Wave–current interaction: Effect on the wave field in a semi-enclosed basin [J].Ocean Modelling, 2013, 70: 152-165.
[17] Shchepetkin A. F., Mcwilliams J. C. The regional oceanic modeling system (ROMS): A split-explicit, free-surface,topography-following-coordinate oceanic model [J].Ocean Modelling, 2005, 9(4): 347-404.
[18] Rusu L., Guedes Soares C. Modelling of the wave–current interaction in the Tagus Estuary [C].Maritime Industry,Ocean Engineering and Coastal Resources-Proceedings of the 12th International Congress of the International Maritime Association of the Mediterranean, Varna,Bulgaria, 2007.
[19] Rusu E. Modelling of wave–current interactions at the mouths of the Danube [J].Journal of Marine Science and Technology, 2010, 15(2): 143-159.
[20] Tolman H. Wind waves and moveable-bed bottom friction[J].Journal of Physical Oceanography, 1994, 24(5):994-1010.
[21] Anderson C., Macklin T., Wolf J. et al. Observations and modelling of the response of along-track SAR interferometry to mesoscale ocean features [J].IEEE InternationalGeoscience and Remote Sensing Symposium, 2003, 3(5):1927-1929.
[22] Chen C., Shigeaki S., Kenji S. Study on a numerical navigation system in the East China Sea [J].Applied Ocean Research, 2015, 53: 257-266.
[23] Ou S. H., Liau J. M., Hsu T. W. et al. Simulating typhoon waves by SWAN wave model in coastal waters of Taiwan[J].Ocean Engineering, 2002, 29(8): 947-971.
[24] Komen G. J., Hasselmann K., Hasselmann K. On the existence of a fully developed wind-sea spectrum [J].Journal of Physical Oceanography, 1984, 14(8): 1271-1285.
[25] Guizien K., Dohmen-Janssen M., Vittori G. 1DV bottom boundary layer modeling under combined wave and current: turbulent separation and phase lag effects [J].Journal of Geophysical Research Oceans, 2003, 108(C1):ID 3016.
[26] Tanemoto J., Ishihara T. A numerical study of wind wave and swell by using wave prediction models and combined wind fields [J].Wind Energy, 2014, 38(4): A124-A131.
[27] Wolfram J., Linfoot B., Stansell P. Long- and short-term extreme wave statistics in the North Sea: 1994-1998 [C].Proceedings of Rogue Waves 2000, Brest, France, 2000.
[28] Benjamin T. B., Feir J. E. The disintegration of wavetrains on deep water. Part 1: Theory [J].Journal of Fluid Mechanics, 1967, 27: 417-430.
[29] Toffoli A., Lefèvre J. M., Bitner-Gregersen E. et al.Towards the identification of warning criteria: Analysis of a ship accident database [J].Applied Ocean Research,2005, 27(6): 281-291.
- 水动力学研究与进展 B辑的其它文章
- Numerical simulation of wave-current interaction using the SPH method *
- The coupling between hydrodynamic and purification efficiencies of ecological porous spur-dike in field drainage ditch *
- Simulation of violent free surface flow by AMR method *
- Experimental research on kinematics of breaking waves *
- Fundamental problems in hydrodynamics of ellipsoidal forms *
- Numerical simulation of cementing displacement interface stability of extended reach wells *

