基于精英策略的多目标规划问题的粒子群算法

黄瑾，张涛，郭阳，胡玉蝶(长江大学信息与数学学院，湖北 荆州 434023)

多目标规划问题大量存在于工程实践与科学研究中，引起了许多科研工作者的高度关注。多目标优化问题往往有2个及以上的目标，各个目标之间相互排斥，为达到其中一个目标通常要牺牲其他目标，难以同时优化所有目标。另外，多目标规划问题的最优解往往不是唯一的，而是一个最优解集合，通常称为Pareto最优解集。与传统的数值优化方法相比，进化算法求解多目标优化问题具有较为明显的优势，进化算法运行结束后，往往可以得到多个Pareto最优解，从而形成了Pareto最优解集[1]。

Schaffer于1985年首次提出了求解多目标优化问题的进化算法——矢量评价遗传算法[2]。从此，多目标进化算法逐步引起了国内外研究者的关注。20世纪90年代提出的算法被称作第1代进化多目标算法，包括Fonseca和Fleming提出的多目标遗传算法[3]、Srinivas和Deb提出的非支配排序遗传算法[4]、Horn和Nafpliotis提出的多目标小生境Pareto遗传算法[5]。20世纪末21世纪初，进化多目标算法迎来第2代，算法的主要特点是精英保留机制。Zitzler和Thiele在1999年提出了强度Pareto进化算法[6]，后来又提出了改进的进化算法——SPEA2算法[7]。2000年Knowles和Corn提出了Pareto外部集的进化算法[8]，后来又提出了改进的进化算法PESA[9]和PESA-II[10]。Erichson、Mayer和Horn于2001年提出了在NPGA基础上改进的NPGA2算法[11]，后来Coello和Pulido研究遗传算法得到了微遗传算法[12]，2002年Deb等提出了相当经典的NSGA-II算法[13]。最近，Deb等采用主分量分析[14]和相关熵[15]的方法研究了高维多目标规划问题的进化算法，在此基础上，Coello等研究了多目标粒子群算法[16]，Gong和Jiao等研究了非支配邻域遗传算法[17]，Zhang和Zhou等研究得到了基于多目标分布估计算法的规律性模型[18]，Zhang和Li研究了基于分解的多目标进化算法[19]。

作为近来提出的一种智能算法，粒子群优化算法的特点与多目标规划问题的结构特征具有优良的匹配性：算法在目标函数、约束函数和模型结构的性能要求上更加宽松，使其可以求解具有一般结构的多目标规划问题；算法以种群为操作单元且实数编码，可以与多目标规划问题的多解特征建立映射关系。利用改进的粒子群算法解决多目标规划问题近来虽然取得了一些结果[13，20～22]，但粒子群优化算法也存在易陷入局优、且所得解分布不均的缺陷。为此，笔者提出一种求解多目标规划问题的基于精英策略的粒子群算法。

1 多目标规划问题的模型及基本概念

假设x∈Rn,f:Rn→Rm,g:Rn→Rq，则多目标规划问题可表述为：

(1)

其中，x为决策变量；f(x)表示目标函数；g(x)为不等式约束函数；S={x|g(x,y)≤0}表示问题(1)的可行域。

定义1如果x*是问题(1)的可行解, 并且不存在x∈S, 使得f(x)f(x*), 则x*为问题(1)的一个最优Pareto最优解, 其中，符号“”表示Pareto偏好。

定义2对于一个给定的多目标优化问题f(x)，所有Pareto最优解构成Pareto最优解集，记作：

P*={x∈S|∃x*∈S,f(x*)f(x)}

定义3所有Pareto最优解对应的目标向量构成多目标问题的Pareto前沿，记作PF*，即：

PF*={f=f(f1(x),f2(x),…,fm(x))|x∈P*}

2 算法描述

算法具体步骤如下：

Step 1 初始化种群P，种群规模为N；初始化循环变量t=0，最大迭代次数为T；

Step 2 基于目标函数f和约束函数g，对每个粒子分配一个非受控等级ND；对具有相同非受控等级值的粒子，基于目标函数f，计算粒子的拥挤度距离CD；

Step 3 将种群P中ND=1的粒子存档于精英集合At；

Step 4 更新粒子的速度和位置：

vj=ωvj+c1r1(pbestj-xj)+c2r2(gbestj-xj)

xj=xj+vj

Step 5 将更新后的粒子重新分配非受控等级ND及拥挤度距离CD；

Step 6 将父代种群Pt和子代种群Qt合并形成种群Rt，基于目标函数f和约束函数g，对Rt中的粒子重新分配非受控等级ND，对具有相同非受控等级值的粒子，计算其拥挤度距离CD；

Step 7 从种群Rt中选取一半的粒子构成新的种群St，先将ND=1的粒子按照CD值降序排列，然后进行依次挑选。当所有的ND=1的粒子挑选完后，再按上述方法挑选ND=2的粒子，直到St中具有N个粒子；

Step 8 更新精英集合At；

Step 9t=t+1，如果t≤T, 转Step 4；否则, 输出At。

算法中，粒子非受控等级排序方法、粒子拥挤度距离计算方法、精英集合更新规则、全局最优粒子的选取及个体最优粒子的选取规则具体阐述如下。

2.1 粒子非受控等级值排序方法

Step 1 假设种群为P，种群规模为N，p表示种群中的粒子;

Step 2 初始化i=1；

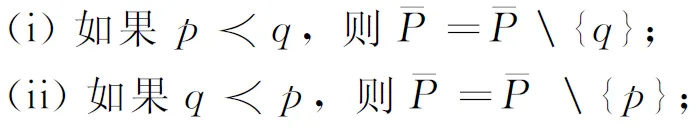
2.2 粒子拥挤度距离计算方法

假设同一级的非受控解集为I, 解集中粒子的个数为l，多目标规划问题的目标函数个数为m。

Step 1 对每个粒子i∈I，初始化I[i]distance=0；

Step 2 对每一个目标函数fj(j∈m):

(i)对所有的粒子i∈I按升序排序；

(ii)令I[1]distance=I[l]distance=∞；

Step 3 从i=2到i=l-1计算粒子的拥挤度距离：

粒子非受控等级排序示意图与拥挤度距离计算示意图如图1与图2所示。

图1 非受控等级排序示意图 图2 粒子拥挤度距离计算示意图

2.3 精英集合更新规则

Step 1 存档控制。假设原精英集合为A，si∈A(i=1,2,…,n)，精英集合的最大容量为N，当前新解为Ns，那么：

(i)若A=Φ，则A=A∪{Ns};

(ii)若A≠Φ，则；

(Ⅰ)若Nssi∈A(i=1,2,…,n)，则A=A∪{Ns}且A=Asi；

(Ⅱ)若Ns与si∈A(i=1,2,…,n)互不受控，则A=A∪{Ns}。

Step 2 网格控制。(i)若Ns在网格范围以内，则正常插入；(ii)如果Ns超出网格范围，重绘网格及重新定位，然后进行插入并删除部分具有较大拥挤度距离的粒子。

图3表示控制器更新规则示意图；图4和图5分别表示被插入的新解在网格范围内时以及新解超出网格范围时进行的插入和删除工作。

图3 控制器更新规则示意图

图4 新解在网格范围内时进行的插入和删除工作

图5 新解超出网格范围时进行的插入和删除工作

2.4 全局最优粒子的选取

Step 1 假设精英集合中的解分布在k个网格中，每个网格中非受控粒子的个数分别为m1,m2,…,mk；

Step 2 计算每个网格的概率值：

Step 3 利用轮盘赌方式选择一个网格；

Step 4 在由Step 3选中的网格中随机挑选一个粒子作为全局最优粒子。

2.5 最优个体粒子的选取

假设当前最好个体粒子为pbest[i]，新解为Ns[i]：

(i)若pbest[i]Ns[i]，则pbest[i]保持不变；

(ii)若Ns[i]pbest[i]，则pbest[i]=Ns[i]；

(iii)若Ns[i]与pbest[i]互不受控，则随机选取当前最好个体。

3 算例分析

粒子群优化算法的相关参数设置如下:r1,r2∈(0,1)，惯性权重w=0.7298,社会系数和认知系数c1=c2=1.49618，种群规模N=100,T=100。计算机运行条件：(CPU:AMD Phenon (tm)ⅡX6 1055T 2.80GHz; RAM:3.25GB) 。利用C#编程进行求解。

算例1

-4≤xi≤4,i=1,2,3，4，5

算例2

-5≤xi≤5,i=1,2，3

算例3

minz1(x)=x1

minz2(x)=g(x)h(x)

其中：

0≤x1≤1，-30≤x2≤30

图6 算例1的Pareto最优前沿面

算例1、算例2、算例3的Pareto最优前沿面分别如图6、图7、图8所示，可以很明显地看出，笔者设计的算法所得多目标规划问题的最优前沿与理论前沿相当接近，并且可以在理论前沿面上均匀分布。

4 结语

笔者设计的多目标粒子群算法具有极强的全局搜索能力，通过3个标准测试函数检验可以看出，算法在非劣解逼近Pareto非劣解的程度上比较显著，非劣解分布比较均匀，所得结果比较稳定。另一方面，相比于传统算法的单一解，笔者所设计的算法得到了一组Pareto解集，从而可以为决策者提供了较大的选择空间。

图7 算例2的Pareto最优前沿面 图8 算例3的Pareto最优前沿面

[参考文献]

[1]Coello C.A comprehensive survey of evolutionary-based multiobjective optimization techniques[J].Knowledge and Information Systems,1999，1(3):269～308.

[2]Schaffer J D.Multiple Objective Optimization with Vector Evaluated Genetic Algorithms[A].International Conference on Genetic Algorithms[C].1985:93～100.

[3]Fonseca C M.Genetic Algorithms for Multipobjective Optimization[J].Formulation Discussion and Generalization，1993:416～423.

[4]Srinivas N, Deb K.Muiltiobjective Optimization Using Nondominated Sorting in Genetic Algorithms[M].MIT Press, 1994.

[5]Horn J, Nafpliotis N, Goldberg D E.A Niched Pareto Genetic Algorithm for Multiobjective Optimization[A].The 1st IEEE Congress on Evolutionary Computation[C].1994:82～87.

[6]Zitzler E, Thiele L.Multiobjective evolutionary algorithms: a comparative case study and the strength Pareto approach[J].IEEE Transactions on Evolutionary Computation, 1999, 3(4):257～271.

[7]Laumanns M.SPEA2: Improving the Strength Pareto Evolutionary Algorithm[R].Technical Report Gloriastrasse, 2001.

[8]Knowles J D, Corne D W.Approximating the Nondominated Front Using the Pareto Archived Evolution Strategy[J].Evolutionary Computation, 2000, 8(2):149～172.

[9]Corne D W, Knowles J D, Oates M J.The Pareto Envelope-Based Selection Algorithm for Multiobjective Optimization[A].International Conference on Parallel Problem Solving From Nature[C].2000:839～848.

[10]Corne D W, Jerram N R, Knowles J D, et al.PESA-II: region-based selection in evolutionary multiobjective optimization[A].Conference on Genetic and Evolutionary Computation[C].2001:283～290.

[11]Erickson M, Mayer A, Horn J.The Niched Pareto Genetic Algorithm 2 Applied to the Design of Groundwater Remediation Systems[A].International Conference on Evolutionary Multi-Criterion Optimization[C].2001:681～695.

[12]Coello C, Pulido G T.A Micro-Genetic Algorithm for Multiobjective Optimization[A].Evolutionary Multi-Criterion Optimization[C].2001:126～140.

[13]Deb K, Pratap A, Agarwal S, et al.A fast and elitist multiobjective genetic algorithm: NSGA-II[J].IEEE Transactions on Evolutionary Computation, 2002, 6(2):182～197.

[14]Deb K, Saxena D K.On finding Pareto-optimal solutions through dimensionality reduction for certain large-dimensional multi-objective optimization problems[R].KanGAL Report，2005.

[15]Saxena D K, Deb K.Non-linear Dimensionality Reduction Procedures for Certain Large-Dimensional Multi-objective Optimization Problems: Employing Correntropy and a Novel Maximum Variance Unfolding[A].International Conference on Evolutionary Multi-Criterion Optimization[C].2007:772～787.

[16]Coello C, Pulido G T, Lechuga M S.Handling multiple objectives with particle swarm optimization[J].IEEE Transactions on Evolutionary Computation, 2004, 8(3):256～279.

[17]Gong M, Jiao L, Yang D.Corrections on the Box Plots of the Coverage Metric in “Multiobjective Immune Algorithm with Nondominated Neighbor-based Selection”[J].Evolutionary Computation, 2009, 17(1):131.

[18]Zhang Q, Zhou A, Jin Y.Errata to “RM-MEDA: A Regularity Model-Based Multiobjective Estimation of Distribution Algorithm”[J].IEEE Transactions on Evolutionary Computation, 2007, 12(1):41～63.

[19]Zhang Q, Li H.MOEA/D: A Multiobjective Evolutionary Algorithm Based on Decomposition[J].IEEE Transactions on Evolutionary Computation, 2007, 11(6):712～731.

[20]Coello C, Lechuga M.A proposal for multiple objective particle swarmoptimization[A].In Congress on Evolutionary Computation[C].2002:825～830.

[21]Yen G, Leong W.Dynamic Multiple Swarms in Multiobjective Particle Swarm Optimization[J].IEEE Transactions on Systems, Man and Cybernetics-Part A: Systems and Humans, 2009, 39(4):890～911.

[22]Tsai S， Sun T， Liu C, et al.An improved multi-objective particle swarm optimizer for multi-objective problems[J].Expert Systems with Applications, 2010, 37(8):5872～5886.