基于小波分析的滚动轴承故障检测方法
王礼鹏
(安徽水利水电职业技术学院 机电工程学院,安徽 合肥 231603)
随着科学技术在现代工业中的快速发展,所使用的设备也变得日趋复杂、智能和高速化,这就需要能准确实时的监测设备的运行安全状态,对相应的技术也提出了更高的要求。监测和管理好设备的安全正常运行,将直接关系到一个企业的发展。如果发生设备故障,可能会使企业无法正常工作,更严重的会使得企业造成巨大的经济损失而停止生产,甚至会危害人的生命健康,造成灾难性的事故。如1972年关西电厂某一轴承发生了断齿的情况,造成机器损毁;1985年山西大同的某电厂发生联轴器断裂;1988年秦岭电厂某汽轮机发生断轴毁机事件,这些都造成了巨大的经济损失。因此,需要深入研究轴承故障检测技术,提高故障的信息分析和处理能力,保证设备的安全正常运行[1]。
对于滚动轴承故障检测方面的研究,最早可以追溯到20世纪60年代,美国学者Guatafsson和Tallian提出了一种基于信号峰值变化的轴承故障检测方法。瑞典的SKF公司在深入研究轴承故障机理后,研制出了一套检测轴承故障的冲击脉冲仪,极大提高了故障检测的精度[2]。新日会社根据振动信号的异常检测,提出了一套轴承润滑态监测系统,可直接检测油膜的破损状态[3]。精工公司研制了一套轴承检测设备,可根据信号的统计峰值数目来监测轴承运行状态[4]。Dver等利用信号分析方法,提出了一种信号峭度的监测方法,信号的峭度与故障状态密切相关。Rei C Wheeler等利用信号的均值和峰值进行轴承故障的检测,取得了很好的效果[5]。Tavlor比较分析了不同故障的频谱特点,提出了一种故障尺寸检测的方法[6]。Randall等分析比较了振动信号的倒频谱和频谱特点,验证了利用倒频谱比功率谱得到的效果好。Mathew等分析了快速傅里叶变换的不足,提出了一种利用自回归模型的方法来检测低速运行的轴承的故障,并取得了很好的结果[7]。
近年来,Antoni建立了一种滚动轴承局部振动模型,同时从原理上给出了轴承故障的机理[8],此模型的建立给轴承故障检测方面的研究奠定了基础。王晓冬等利用小波重构原理,提取得到了轴承外圈的频率特征。Endo等利用自回归对振动信号进行建模,并采用熵卷积的方法对信号进行去噪,从而提高故障检测的准确度[9]。张俊红等提出了一种EMD算法与ICA相结合的信号降噪方法,利用EMD分解振动信号可以克服观测通道数限制的缺陷[10]。
时频分析是一种常用的针对非线性非平稳信号的分析方法,可以根据信号的时频特征来提取有用的信息。其中,小波分析是一种有效的时频分析方法,将其用来提取滚动轴承故障的时频特征信息,根据得到的特征来检测滚动轴承的故障。本文利用小波分解故障轴承的信号和正常轴承的信号,通过比较各层的峰值特点来检测故障轴承,实验验证了本方法的有效性。
1 滚动轴承的故障机理
滚动轴承是机器设备的关键部分,在设备系统中扮演着非常重要的角色。它的作用主要是利用两轴承间的滚动摩擦来代替原来面与面间的滑动摩擦,从而减少由摩擦带来的能量损失。滚动轴承可以承担来自各方的负荷,根据不同的滚动方式,轴承可分类为球形、圆柱形、鼓形和锥形滚动轴承。一般的轴承架构通常包含内、外圈、支撑架和滚轮四个部分。图1给出了一种典型的滚动轴承示意图。轴承的外圈通常固定在基座上不动,而其内圈和传轴一起转动,也有少数轴承内、外圈和传轴一起转动。轴承的滚轮一般在内外圈之间滑动,这样可以大大减少各部件间的摩擦力,减少系统的摩擦损失。

图1 滚动轴承结构图
轴承在运行一段时间后,会出现或多或少的故障情况,引起轴承故障的原因较多,通常有轴承部件装配不合理、工作环境恶劣、轴承过载以及部件腐蚀等。即便是在各种理想条件下运行,轴承一般也会出现磨损或断齿的现象[11]。如果轴承出现故障没有及时整修,则会使得轴承故障得以加剧,更甚者会导致系统奔溃。在实际工作中,轴承故障形式和原因各异,常见的故障来源有以下三种[12]:
1)轴承结构发生变形。在轴承超负荷运行时,轴承的部件会发生错位或变形等情况。
2)轴承部件的制造误差。这类误差会使得轴承不能在合理的状态下运行,同时导致系统出现故障。
3)故障轴承引起的振动。在轴承运行时,如果系统中残存异物或轴承出现断裂等情况,通常会导致轴承故障振动。
2 小波变换的基本原理
小波分析是一种有效的数学分析工具,已经应用于很多领域。小波分析在本质上是利用多分辨技术来进行时频分析的一种方法,它能有效的克服经典的傅里叶变换在局部特性表示方面的不足,同时由于利用了多分辨技术,提高了频率分辨率。目前在滚动轴承故障检测分析方面,小波分析有很大的研究发展空间。小波分析利用带通滤波原理,可以通过合适的小波基选择进行诊断信号的分解,从而可以得到一系列频带中信号的信息变化特性,最后依据这些变化特征提取到反映轴承振动规律的信号特征量,根据这些特征量来进行轴承故障的监测。小波分析利用多分辨技术,可以在不同尺度下描述信号的特征。目前,小波分析已广泛应用于各领域中[13]。
小波,即小段时间序列的波形,表示有限时间段内平均值为0的波形。小波的确切的定义为:设基小波函数ψ(t)∈L2(c),L2(c)表示一个平方可积的复函数空间,基函数ψ(t)须满足:
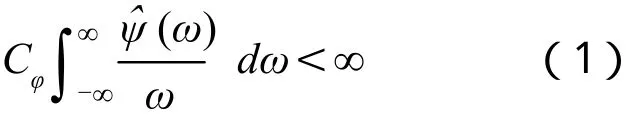
式中(ω)为ψ(t)的傅里叶变换。公式(1)中暗含一条件,即(0)=0,该条件说明基函数具有零均值。
小波基函数在尺度和时间维进行变换后,得到一个小波簇:
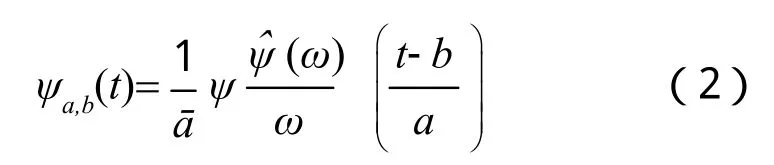
其中,a表示尺度参数;b表示位置参数。a是用来调整子波覆盖的频率范围,b用来调整子波的时域位置,系数1/ā用来实现小波能量的归一化。对于某一时变信号x(t),其小波基的表示可定义为:
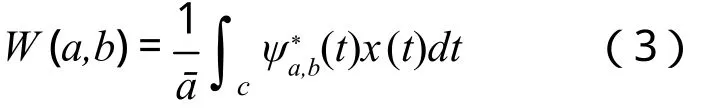
式中ψa*,b(t)为ψa,b(t)的复共轭;C表示复数域。位置参数b和尺度参数a在取值范围内连续变化。根据公式(3)可以看出,小波的变换系数W(a,b)是由一个子小波与原信号的内积计算得到,子小波的位置系数为b,尺度参数为a。小波的变换系数表示基函数与信号的相似程度,W(a,b)越大,表示两者越相似。因此,有效提取信号的特征信息,需要选择与信号相似程度大的基函数,合适的小波基可得到有效的小波分解。当选择了合适的小波基后,就会使特征成分在时间尺度相平面上某处集结为高幅值的能量块,其中,与子小波差别大的能量分散到尺度时间平面上,这样就可以很清楚的看出故障信息,从而实现了故障的检测识别[14]。
3 滚动轴承故障诊断的小波分析法
基于小波分析的信号处理方法,其步骤为:
1)采样,对收集的信号,通常需要进行采样,不同的应用条件,其采样率会不同。
2)信号分解,在得到采样数据后,通常对其进行多层分解,分解可以得到各层的小波系数。
3)信号压缩,根据小波系数的大小,可以舍弃一部分系数小的分量,从而达到信号压缩的目的。
4)信号重构,对压缩后的信号数据,可以根据系数重构原始信号。
由于轴承自身的结构特点,在其运行一段时间后会出现一些装配结构误差和磨损等故障,这些故障一般来源于轴承超负荷运行,轴承故障会是设备产生振动信号。轴承根据其信号的不同特点可以分为损伤故障和磨损故障,损伤故障通常发生在部件表面,当损伤点经过某部件的表面时,传感器会接收一冲击信号,此冲击信号为一宽带脉冲信号,这样的宽带信号能涵盖系统的各频率带。损伤故障产生的振动信号通常振幅较小,容易被大的振动信号掩盖,一般不能通过信号的功率谱进行分辨。
小波分析具有时间和频率的多分辨率的特点,对于故障引起的振动信号,通过小波分析可以在多分辨率的细节上能清楚的进行分辨,因此,利用小波分析来检测滚动轴承故障,是一种有效的检测方法。通常先对采集的信号进行小波变换,根据小波系数,对包含有用信息的信号进行重构,然后,对重构的信号进行Hilbert变换,分析得到的频谱特点进行故障检测。
这里选取了1组正常轴承数据(normal880.mat)(见图2),1组磨损故障数据(mosun880.mat)(见图3),一组外圈故障数据(duanchi880.mat)(见图4),利用Matlab软件进行故障分析。信号采样频率均为12 000 Hz。
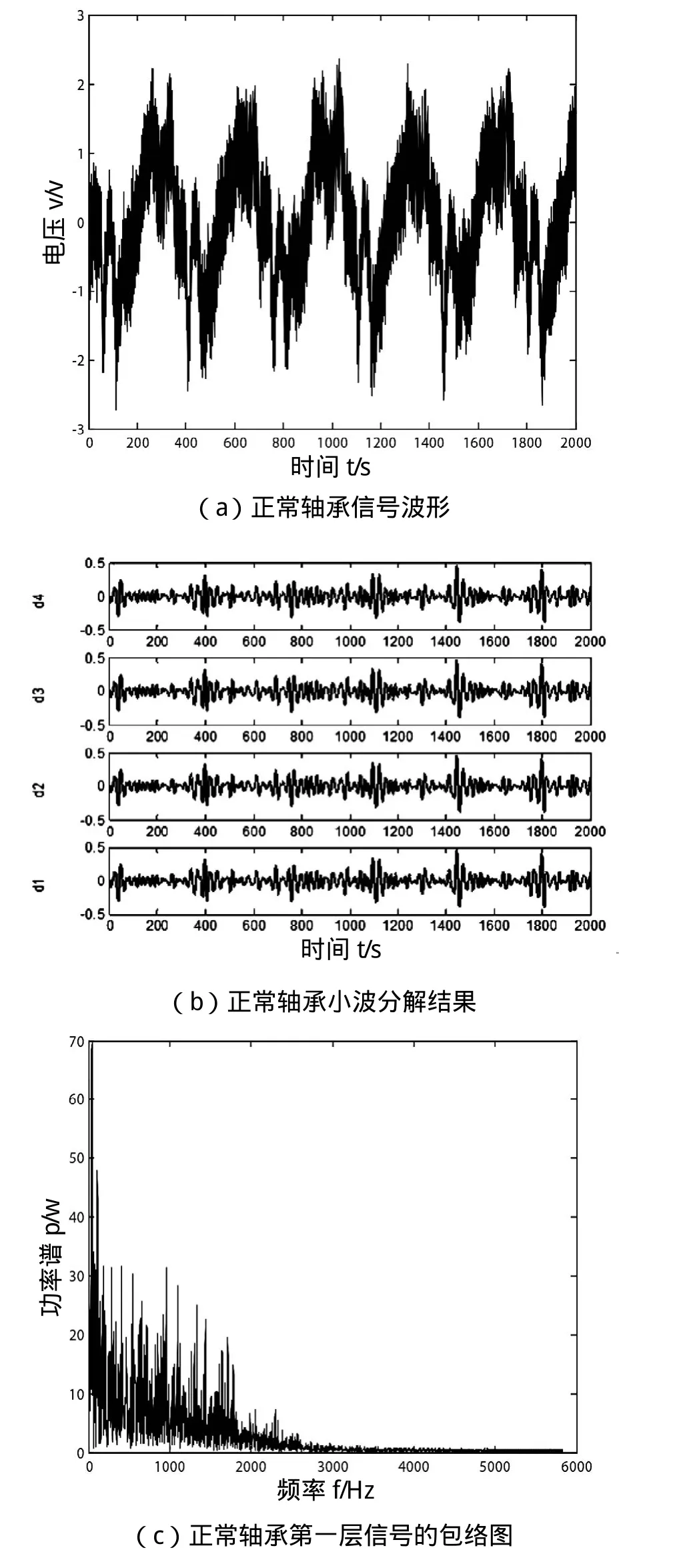

图2 正常轴承信号的小波分析
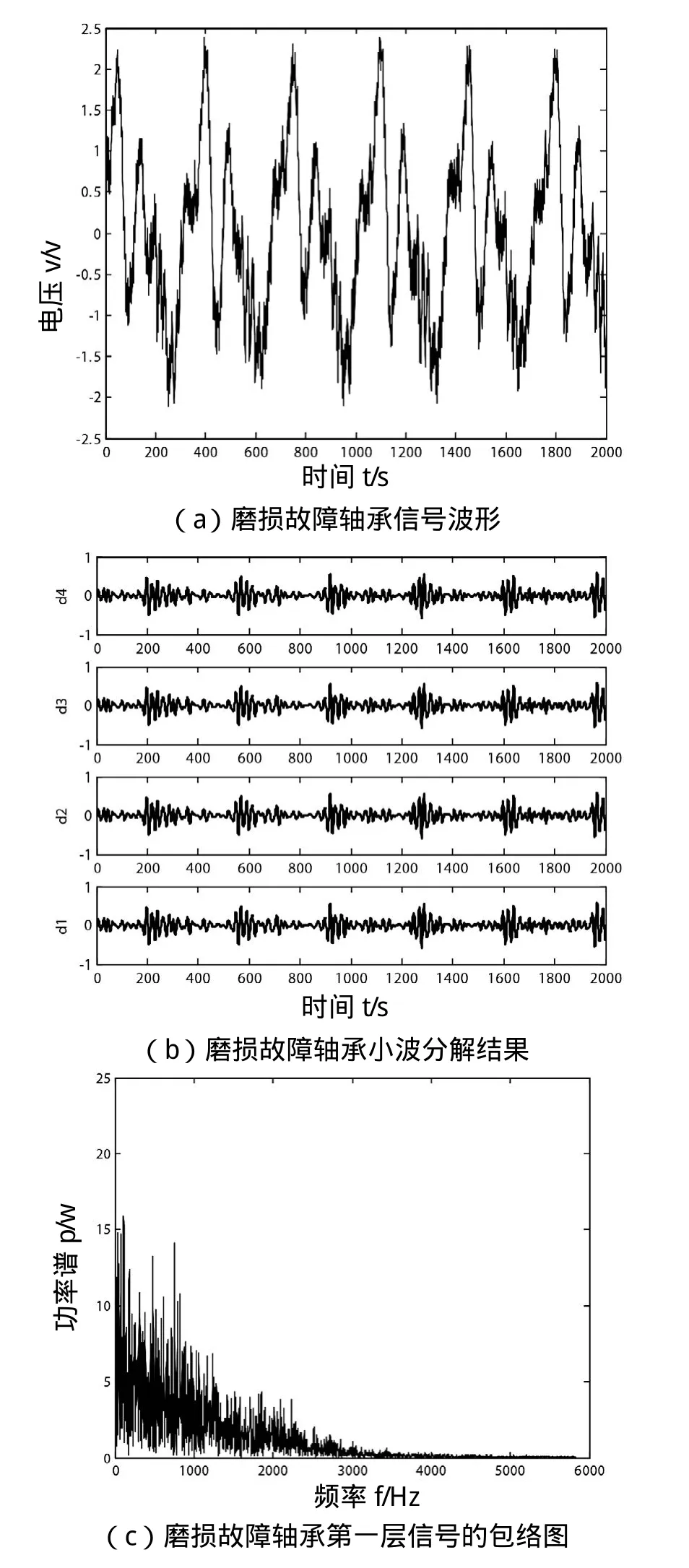
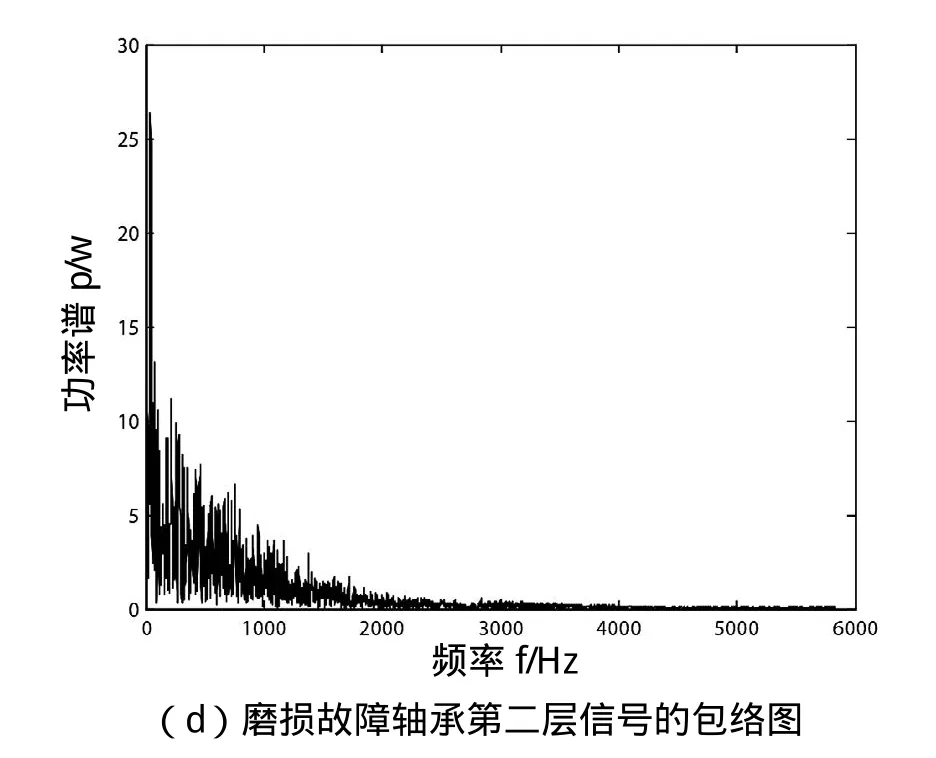
图3 磨损故障轴承信号的小波分析
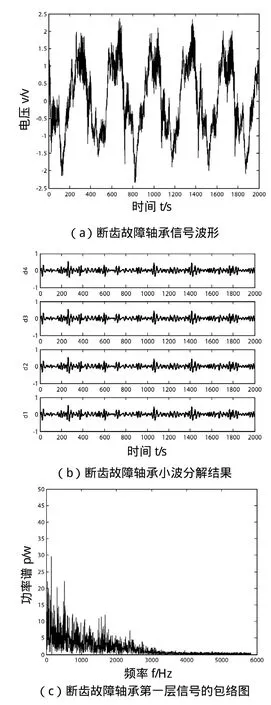
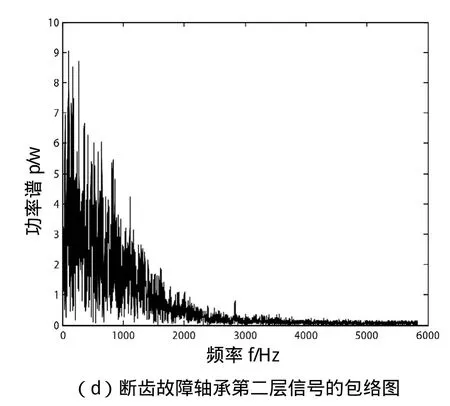
图4 断齿故障轴承信号的小波分析
根据图2、3和4可以看出,在没进行小波变换前,正常轴承的原始振动信号相较于磨损故障和断齿故障的2组振动信号,其采集的数据较密,但不能根据这些波形判断出是否发生故障。对3组振动信号进行小波分解后,取每组信号的第一、二层包络进行显示,即上述图中的(c)和(d),从图中可以看出,正常轴承的第一、二层包络中频率在0附近出现了较高的峰值,而磨损和断齿故障的包络频谱图在频率为0附近没有出现峰值,由此可以判断出是否出现故障。
[1]陈大禧,朱铁光.大型回转机械诊断现场实用技术[M].北京:机械工业出版社, 2000:15.
[2]O.G Gustantsson,T.Tallian.Detection of Damage in Assembled Rolling Bearing[J].Transactions of the ASLE,l962,5:197-209.
[3]D.DyerR.M.Stewan.Detection of Roning Element Bearing Damage by Statistical Vibration Analysis[J].Transactions of the ASME Joumal of Mechanical pesign,1978(4):229-235.
[4]T.G Wheeler.Bearing Analysis Equipment Keeps Down Time[J].Down Plant Engineering,l968(5): 87-89.
[5]R.B.Randan.Analysis Techniques for Diagnosis of Gear and Bearing Faults[C].Proceedings of CSMDT 86.Shenyang China,1986: 387-393.
[6]雷继尧,程善同.轴承疲劳诊断仪[C].重庆大学会议资料, 重资(86)004号.
[7]屈梁生,何正嘉.机械故障诊断学[M].上海:上海科学技术出版社,1986:23.
[8]J Antoni,R B Randall.A Stochastic Model for Simulation and Diagnostics of Rolling Element Bearings With Localized Faults[J].Journal of Vibration and Acoustics,2003,125:282-289.
[9]H Endo,R B Randall.Enhancement of autoregressive model based gear tooth fault detection technique by the use of minimum entropy deconvolution filter[J].Mechanical Systems and Signal Processing,2007,21:906-919.
[10]张俊红,李林浩,马文朋,等.EMD-ICA 联合降噪在滚动轴承故障诊断中的应用[J].中国机械工程,2013(11):1468-1472.
[11]苏文胜.滚动轴承振动信号处理及特征提取方法研究[D].大连:大连理工大学, 2010.
[12]王树梁.基于HHT的提升机天轮轴承故障诊断方法研究[D].济南:山东大学, 2011.
[13]马秀红,曹继平,董晟飞.小波分析及其应用[J].计算机技术与发展,2003 (8):93-94.
[14]孙云莲,刘敦敏.时频分析与小波变换及其应用[J].武汉大学学报(工学版), 2003 (2):103-106.

