数控滚齿机伺服控制系统的性能优化研究

张鹏远

（中国重汽集团大同齿轮有限公司， 山西 大同 037000）

引言

随着中国制造业的快速发展，零件的加工精度成为制造行业的关注重点。加工设备也由传统的机械式加工方式发展为数控式加工，数控滚齿机则是数控加工设备中的重要组成部分。然而传统机加工设备中的伺服驱动控制系统，大都存在只能控制单轴的运行情况，而不能保证机床多轴的同步运行，当遇到突然加载情况时，各轴之间的同步运动性较难保证，严重影响着数控机床的加工精度。因此，有必要开展数控滚齿机伺服控制系统的性能优化研究[1]。

1 伺服控制系统组成及工作原理

结合实际产品特点，数控滚齿机伺服控制系统主要由速度传感器、位置传感器、伺服电机、功率转换器、速度控制器、电流控制器等部分组成。伺服系统的工作原理图如图1所示。通过控制器将数控中心的速度信号和实际检测速度信号进行对比，生成具有一定误差的速度信号。由于该速度信号为直流信号，而驱动电机所需的信号为交流信号，因此，需将该速度信号进行直流变交流化处理，转化后的交流信号相位由转子磁极决定，信号频率由转子的旋转速度决定。通过将磁极位置信号和直流电流信号相乘，可在乘法器输出端得到频率较高、幅值更大的正弦交流电流信号，通过电流与驱动电机转子的磁通作用，产生了较大的电磁转矩，从而驱动了永磁同步电机的驱动，形成了一套完成的伺服控制系统，实现了数控滚齿机的正常运转[2]。

图1 伺服控制系统工作原理图

2 伺服控制系统控制器模型建立

通过伺服系统控制器，可将数控中心传递的速度信号和检测的实际信号进行对比，并通过放大器将偏差信号进行放大输出，实现速度信号的输出控制。其电路结构图如图2所示。其中，反馈电阻R1、C1和输入电阻R0等元件组成了伺服系统的比例积分放大器。

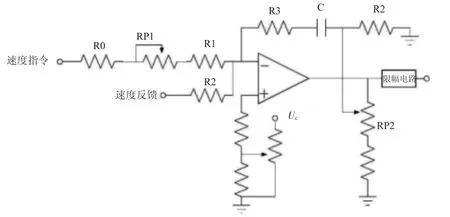
图2 伺服系统控制器电路结构图

式中：KP为控制器的放大系数，τ为控制器时间常数。

令τ1=KPτ，则控制器数学模型函数为：

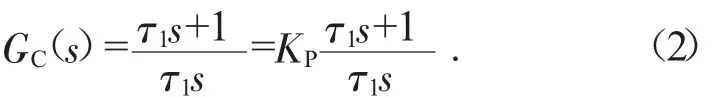
由图2可知，该系统的传递函数为：

3 伺服系统PI交叉耦合控制算法建立

PI控制器集成了比例—积分两种控制方式优点的控制算法，在零件轮廓成形、异性结构加工等精度控制方面具有较大优势，主要由交叉耦合误差模型和轮廓误差补偿分配器等部分组成，通过综合考虑各运动轴之间形成的同步误差，采用分配补偿规律，降低各轴同步误差，提高数控机床的加工精度。其原理为：利用比例控制器来提高系统的响应时间，避免受到外界干扰信号的影响，利用积分控制器消除系统的稳态误差。该控制算法主要通过控制器的u（t）输出将信号进行放大，并将偏差信号e（t）进行积分，其表达式见式（3）。PI控制器框示图见图3。

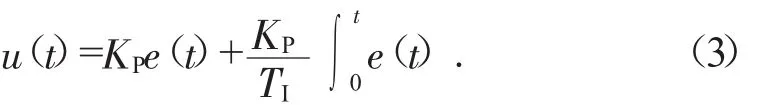
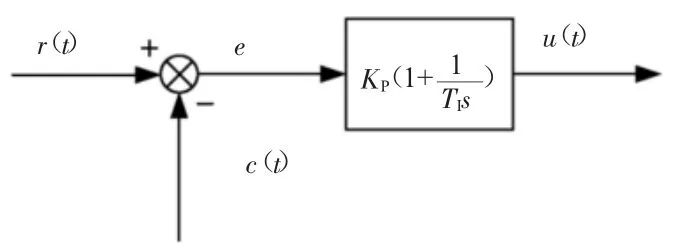
图3 PI控制器框示图

由于在数控滚齿运转过程中，需保证滚刀主轴（B轴）和工作台回转轴（C轴）转速的同步运转，因此引入了两轴的同步误差概念，其公式定义如下：

通过对B轴、C轴转速的分析，得出了B轴、C轴的实际转速公式，如下：

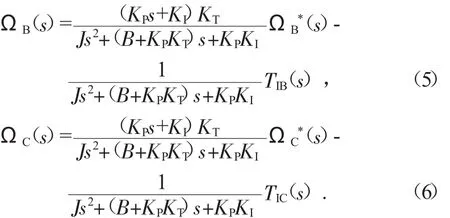
由此，可算出PI交叉耦合控制算法下同步误差为：

其系统的控制原理框图如图4所示。

4 伺服系统加载状态仿真分析

结合前文建立的伺服系统控制器数学模型，采用MATLAB仿真软件，利用所建立的PI交叉耦合控制算法，开展了伺服系统在加载状态下PI交叉耦合控制的仿真分析研究。

图5为数控齿轮机伺服系统在加载状态下PI交叉耦合控制方式下的速度响应曲线。由5图可知，当在0.005 s和0.04 s时，系统的B轴和C轴的速度发生了短暂的振动现象，且B轴较C轴振动得更剧烈，之后两轴的速度均呈现相对稳定的变化过程；同时，B轴的振动速度比C轴的更高，这是由其自身结构特点所决定。由此可知，利用PI交叉耦合控制算法，不仅不会提高转轴的运动性能，反而可使数控滚齿轮各轴的速度响应更敏感，更直观地反映转轴的振动幅度，从而使驱动系统能更好地对转轴进行监测控制，提高了系统的控制精度[3-4]。

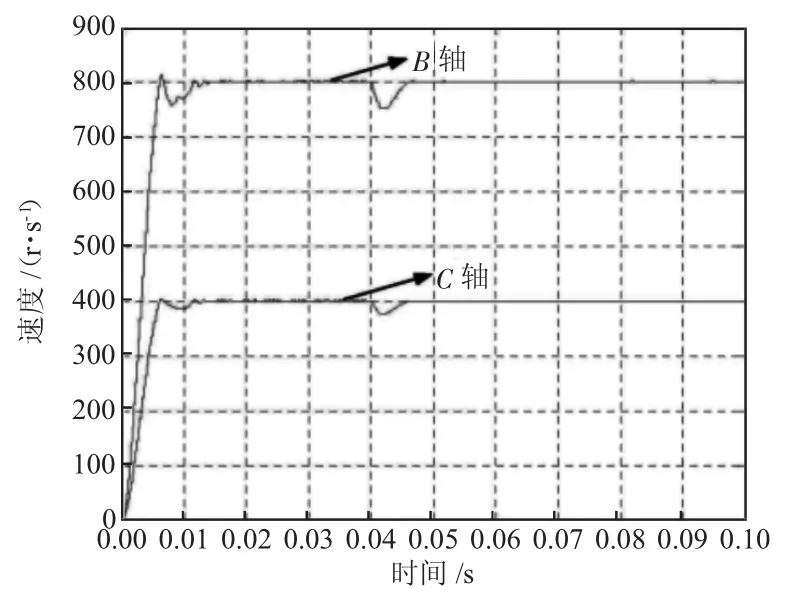
图5 伺服系统加载状态下的速度响应变化曲线

图6 为加载状态下交叉耦合控制与传统控制同步误差对比曲线图。由图6可知，伺服系统在开始阶段和突然加载后，交叉耦合控制算法下的同步误差均比传统的控制算法下的同步误差更小，整个伺服控制系统更加稳定。由此可知，将PI交叉耦合控制算法应用到数控滚齿轮伺服控制系统中具有更好的控制优势，能实现对B轴和C轴同步误差的有效控制，降低数控机床的同步误差，保证了数控机床的加工精度，很好地满足了工程的实际需求[5-6]。

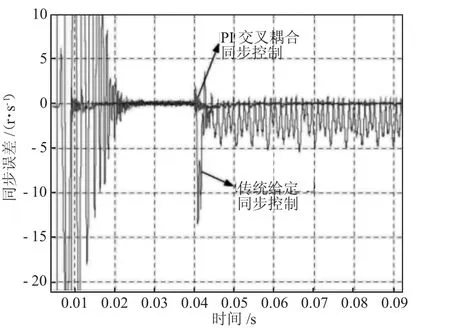
图6 PI交叉耦合控制与传统控制同步误差对比图

5 结论

与传统控制算法相比，基于PI交叉耦合控制算法的伺服控制系统具有更高的控制精度，能更加有效地控制和降低数控机床的同步误差，保证了数控机床的加工精度；同时，在数控机床驱动系统设计过程中，可参考此算法对控制系统进行设计优化。该研究实现了传统控制算法的理论突破，对数控滚齿机伺服控制系统的性能优化设计具有重要的参考意义。

[1]郭庆鼎，孙宜标.现代永磁电动机交流伺服系统[M].北京：中国电力出版社，2006.

[2]卢绍青.数控机床通用误差补偿技术研究[D].北京：北京工业大学，2001.

[3]沈琛.YKQ31300数控滚齿机立柱的静动态特性分析及优化设计[D].武汉：湖北工业大学，2015.

[4]黄亮.大型数控滚齿机伺服系统同步控制研究[D].重庆：重庆大学，2011.

[5]姜小飞.数控滚齿机热误差补偿技术研究[D].合肥：合肥工业大学，2013.

[6]李先广，杨勇.数控滚齿机滚刀主轴振动特性研究[J].机械工程学报，2017，53（1）：130-139.