光学元件面形评价参数的稳定性及关联性*

刘佳妮，田爱玲，刘丙才，朱学亮，王红军

(西安工业大学 光电工程学院，西安 710021)

光学元件的面形精度决定其成像质量，也是决定仪器总体质量的重要因素之一[1]，因此对光学元件的测量及评价尤为重要.不同的研究领域，使用的评价参数不同.近年来，数字波面干涉仪的发展，使得光学元件的测量更加方便、准确，如何对测量结果进行评价成为重点研究的问题.目前，在低频面形检测中，人们大多使用峰谷值(Peak to Valley，PV)或均方根值(Root Mean Square，RMS)来评价光学元件的面形质量[2-3].这里的PV值仅指被检波面上最高点、最低点的差值.波面是指由标准面或被测面反射的光，其携带了反射面面形的偏差信息.随着干涉测量技术的发展，干涉仪的精度和分辨率显著提高，使用两点PV值进行面形评价出现了很多弊端，最大的问题是测量结果有较大的波动性.为了更准确地评价光学元件的面形，国际上已经出现了一些PV相关的评价方式，包括PVm、PV20、PVq和PVr等参数[4-7].但是，由于标准没有统一，使用的评价参数不同会导致结果具有很大的差异.

目前，国内外研究人员均对评价参数进行了研究.文献[2]对峰谷值和均方根值的联系进行了研究，得到抛光后的光学表面经泽尼克多项式拟合后，其PV值与RMS值约为3～5倍的关系，而未经泽尼克拟合的实测值约为7～10倍的关系.文献[4-5]提出了一种稳定的峰谷值PVr参数.文献[6]通过对峰谷值的分析，得到了PV20、PVq和PVr对测量结果的评价合理性和重复性优于PV值.文献[7]通过实验探讨了三种评价标准PV、PV20和PVq，得到使用PV20和PVq可以获得更可靠的评价结果.目前系统分析PV相关参数以及参数间的关系未见报道.在实际测量中，难以选取合理的评价参数.同样的测量方法，选择的评价参数不同，得到的测量结果有很大差异.所以，寻求一种相对稳定的评价指标对测量结果进行准确评价，尽可能使测量结果统一化.

文中以传统抛光方式下的平面光学元件为研究对象，得到了使用不同评价参数对平面光学元件低频信息评价的结果，对PV相关评价参数的稳定性进行了分析，同时研究了PV相关参数和RMS值的关系，为评价光学元件的面形质量提供了重要的理论参考.

1 面形评价参数的稳定性分析

在实际的光学测量中，会受到噪声、毛刺点等干扰，使得测量结果存在一定的误差.不同的评价参数对这些干扰的敏感度是不同的，为了使测量结果尽可能的统一化，应正确选择评价参数，尽可能的去除这些噪声干扰，使得测量结果稳定化.因此需要对面形评价参数的稳定性进行分析.

1.1 主要面形评价参数及定义

在目前光学元件的检测中，通常使用PV或RMS来评价光学元件的表面面形质量.为了克服两点PV值所存在的弊端，提出了一些与PV相关的评价参数，如PVm、PV20、PVq和PVr等，主要评价参数的定义见表1.

表1 主要评价参数定义

1.2 不同PV评价参数的稳定性

采用泽尼克多项式模拟一个近似理想的波面图[8](PV=4.29 nm)，如图1所示，表2给出了理想波面的PV、PVm、PV20、PVq和PVr等不同评价参数，以及各个参数相对于原始波面两点PV值的变化百分比.

从表2中可以看出，对于理想波面，采用PV、PVm、PV20、PVq和PVr五种参数评价相对于原始波面PV值的变化百分比均小于15%，说明对于理想波面而言，无论采用哪种评价参数，其评价结果相差不大.

选择口径为∅100 mm，PV值为λ/10(λ为激光波长)的标准平面镜作为待测样片，利用实验室的zygo干涉仪进行面形检测.在测量结果中去除倾斜和常数项(去除部分测量误差)，并将有效域设置为95%(去除边缘虚假峰齿)，得到平面镜的原始面形数据.针对这个原始数据，计算得到PV、PVm、PV20、PVq和PVr一组不同评价参数.在得到的面形原始数据中，分别添加单个毛刺点和多个毛刺点，进行计算得到PV、PVm、PV20、PVq和PVr一组评价参数.其中添加单个毛刺点后的波面PV值为112.31 nm，添加多个毛刺点后的波面PV值为170 nm.图2(a)所示为原始波面图，图2(b)为添加单个毛刺点后的波面，图2(c)为泽尼克拟合后的波面，图2(d)为拟合后波面与添加毛刺点波面的残差图.

图1 理想波面图

评价方式PV/nmPVm/nmPV20/nmPVq/nmPVr/nm计算结果4.294.284.274.083.75变化百分比/%0.230.474.9012.59

图2 波面图

对比图2(b)、2(c)可以看到，通过泽尼克多项式拟合可将波面的高频毛刺点剔除.图3给出了添加毛刺点前后的PV、PVm、PV20、PVq和PVr等面形评价结果.同时计算可得，经过五种评价方式进行对比后，PVm、PV20、PVq和PVr相对于PV值的变化百分比分别为4.15%、25.72%、63.41%和54.70%，相对于理想波面而言，其相对变化量明显增大，说明对于实际测量而言，采用五种评价方式评价，结果差异很大.

图3 添加毛刺点前后的不同评价结果

从图3中可以看出原始波面、添加单个毛刺点以及添加多个毛刺点的波面经过五种评价方式进行计算的结果，以及各参数的变化趋势.通过对比添加毛刺点前后的五种评价方式计算结果，可知PV、PVm和PV20的变化量比较大，即这三个参数受毛刺点的影响比较大，而在实际测量过程中，表面微观疵病如麻点对测量结果影响很大，随机噪声对测量结果也有影响，但对成像影响不大，若采用PV、PVm和PV20来评价是不准确的.而PVq、PVr的变化量很小，即对毛刺点并不敏感，故这两种指标的稳定性比较好.

1.3 不同评价方式的重复性比较

重复性是判断测量系统好坏的一个重要指标，通常测量仪器会给出该指标.重复性指用相同的测量方法，由同一操作人员，使用同一仪器，相同样片所做多个单次测试结果.选择口径100 mm，PV值为λ/10(λ为激光波长)的平面镜作为待测样片，使用zygo干涉仪对该平面镜进行55次测量，导出每次测量的原始三维数据，根据评价参数的计算方法，对波面进行评价，分别计算得到五种不同评价参数下的面形结果，如图4所示.

从图4中可以看出，PV、PVm、PV20和PVq的波动幅度很大，说明不能用这四种评价参数来评价测量的重复性，而PVr的波动范围较小，说明PVr可以更准确地评价测量的重复性.这与五种评价方式的去除点数，拟合方式有关，其中PVr的计算需要对原始数据进行泽尼克多项式拟合，拟合的过程中会去除一些毛刺点、噪声，因此得到的结果是相对稳定的.通过计算PV、PVm、PV20、PVq和PVr各评价参数的标准偏差分别为6.21 nm、6.47 nm、4.58 nm、4.30 nm和4.25 nm，可知PVr的数值分散程度最小.说明PVr相对于其他四种参数重复性更好，更稳定.

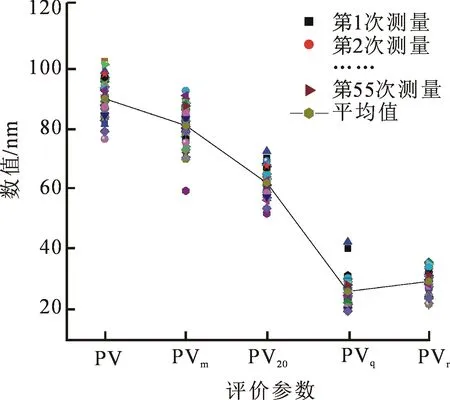
图4 不同评价方式的重复性比较

2 面形评价参数的关联性分析

通常在评价光学元件的面形质量时，大多仅使用单一的评价参数PV或RMS进行评价.而在实际测量中发现，具有相同PV值的波面，其RMS值相差很大；同样地，具有相同RMS值的波面，其PV值一般也相差很大.因此，单一的评价参数是否能准确的反映面形质量，需要进一步研究讨论.通过对传统抛光加工方式下平面镜面形进行分析，对评价参数之间的关系进行研究，对其关联性进行讨论，分析使用单一评价参数评价波面的可行性.

2.1 仅考虑单项像差时各评价参数的关联性分析

在光学设计中，有时会设计某个单像差系统，用于研究像差的校正问题.对于仅含有单项像差的波面进行研究，分析单一的评价参数是否能准确的反映面形质量.根据泽尼克项和像差的对应关系[9-12]，见表3，结合实际测量数据，得到泽尼克前36项系数，设定单项泽尼克多项式的系数，用来拟合具有单项像差的波面.选用购置的一组传统抛光加工的平面镜(口径为40 mm、厚度5 mm、面形PV值小于λ/4)，使用zygo干涉仪测量得到其三维数据，利用泽尼克拟合得到每个样片表面的泽尼克多项式.通过对比泽尼克各项和像差的对应关系，提取相应项的泽尼克系数用来拟合仅含有单项像差的波面，并计算相应的各面形评价参数.对PV、PVm、PV20和PVq等参数与RMS评价参数的关联性进行研究，没有对PVr进行计算，这与PVr的定义有关.仅含有单项像差的波面是由单项泽尼克系数拟合得到，而拟合前的波面是含有多项像差的，无法获得剩余均方根值，无法对PVr进行计算.

表3 泽尼克前9项和像差的对应关系

注：ρ极径；θ′为极角.

文中分别考虑了仅含有离焦、像散、彗差、球差时，PV相关参数与RMS之间的关系.其中，仅考虑离焦项时，根据泽尼克项和像差的对应关系，即设定泽尼克多项式的系数Z3；仅考虑像散项时，即设定泽尼克多项式系数Z4、Z5；仅考虑彗差项时，即设定泽尼克多项式系数Z6、Z7；仅考虑球差项时，即设定泽尼克多项式系数Z8.分别使用不同的泽尼克多项式系数拟合波面，经PV、PVm、PV20、PVq和RMS等评价参数计算，并得到PV相关参数与RMS之间的关系.仅考虑离焦时，各参数之间的关系，见表4.

表4 考虑离焦时各参数之间的关系

从表4中可知，仅考虑离焦时，不同泽尼克系数拟合后波面的PV值大不相同，但PV/RMS、PVm/RMS和PV20/RMS趋于3.47，PVq/RMS趋于3.43.说明对于仅含离焦的波面而言，使用单一的PV值来评价时，会得到其对应的RMS值.因此，评价仅含有离焦项的波面时，仅需使用单一的评价参数就能评价其面形质量；同理得到仅考虑像散、彗差、球差时，PV相关参数与RMS之间的关系，将得到的参数间的关系做成直方图，如图5所示.从图5可知仅考虑像散时，PV/RMS和PVm/RMS趋于4.90，PV20/RMS趋于4.88，PVq/RMS趋于4.58；仅考虑彗差时，PV/RMS和PVm/RMS趋于5.65，PV20/RMS趋于5.62，PVq/RMS趋于4.83；仅考虑球差项时，PV/RMS、PVm/RMS和PV20/RMS趋于3.36，PVq/RMS趋于3.32.表明对于仅含单项像差的波面而言，使用单一的PV值来评价时，得到其对应的RMS值.因此，评价仅含有单项像差的波面时，仅需使用单一的评价参数就能评价其面形质量.

图5 仅考虑单项像差参数关系

2.2 一般面形测量中各评价参数关联性分析

在一般的面形测量中，不可能仅提取波面的某些低阶像差来研究，所以需要对实际测量的三维数据进行分析.

使用同一平面镜，进行多次测量，对参数之间的关联性进行分析.将口径为100 mm，PV标称值为λ/10的平面镜作为待测镜片，使用zygo干涉仪对该平面镜进行55次测量，获得三维数据，计算PV相关参数与RMS之间的比值，做成散点图如图6所示.

图6 多次测量同一样片的参数关系

由图6可以看出，对于同一个样片而言，其PV/RMS、PVm/RMS和PV20/RMS波动性幅度很大，无法得到一个确定的数值.PVq/RMS和PVr/RMS波动幅度相对来说是很小的，大致在3～7倍的范围.表明PV与RMS的关系并不是一一对应的，此时，采用单一的评价参数进行评价是不合理的，需要PV值和RMS值综合来评定光学元件的质量.

使用多个样片，进行单次测量，对参数之间的关联性进行分析.使用zygo干涉仪对42个不同PV值的平面镜进行测量，计算得到PV/RMS、PVm/RMS、PV20/RMS、PVq/RMS和PVr/RMS，如图7所示.

图7 单次测量多个样片的参数关系

由图7可以看出，PV/RMS和PVm/RMS波动性幅度最大且大致相同，大致在5～13倍的范围.PV20/RMS大致在5～12倍的范围，PVr/RMS大致在5～9倍的范围.PVq/RMS波动幅度最小，比值大致在4.5～6.5倍的范围.可见PV与RMS的比值没有固定的关系，因此，在评价时需要使用PV和RMS值综合评定光学元件的质量.

3 结 论

1) 对于理想波面，采用PV、PVm、PV20、PVq和PVr五种参数评价，相对于原始波面PV值的变化百分比均小于15%；对于一般的面形测量，PVq和PVr对毛刺点不敏感且重复性好，PVq和PVr的稳定性优于PV、PVm和PV20.实际光学加工时，PVr的计算复杂，在评价光学元件低频信息时使用PVq参数来评价.

2) 评价参数关联性分析结果表明,传统抛光加工方式下的光学元件，仅考虑单项像差时，可使用单一的PV或RMS值评定光学元件的面形质量.一般的面形测量，可通过PV和RMS综合评定光学元件的面形质量.

3) 对于传统抛光加工方式下一般的面形测量，PVq与RMS的比例波动最小，PVq参数判断测量结果的准确性优于其它参数.

参考文献：

[1] 尤科伟,张艳丽,张雪洁,等.光学元件表面缺陷相对位置分布对近场光束质量的影响[J].中国激光,2015,42(3):255.

YOU Kewei,ZHANG Yanli,ZHANG Xuejie,et al.Influence of Relative Position of Optical Component Surface Defects on Near Field Beam Quality[J].Chinese Journal of Lasers,2015,42(3):255.

(in Chinese)

[2] 戴斌飞.面形精度评价方法研究[D].苏州:苏州大学,2005.

DAI Binfei.Study on Methods for Assessing Precision of Optical Surface[D].Suzhou:Soochow University,2005.(in Chinese)

[3] LAWSON J K,AIKENS D M,ENGLISH R E,et al.Surface
Figure and Roughness Tolerances for NIF Optics and the Interpretation of the Gradient,P-V Wavefront,and RMS Specifications[J].Proceedings of SPIE,1999,3782(1):510.

[4] EVANS C J.Uncertainty Evaluation for Measurements of Peak-to-valley Surface form Errors[J].CIRP Annals-Manufacturing Technology,2008,57(1):509.

[5] EVANS C J.PVr-a Robust Amplitude Parameter for Optical Surface Specification[J].Optical Engineering,2009,48(4):043605.

[6] 高波,李瑞洁,魏小红,等.关于光学元件面形评价参数峰谷值(PV)的分析[J].应用光学,2010,31(6):1046.

GAO Bo,LI Ruijie,WEI Xiaohong,et al.Peak-to-valley Parameter of Optical Component[J].Journal of Applied Optics,2010,31(6):1046.(in Chinese)

[7] 陈科伟.手机镜片非球面面形精度PV评价标准分析[J].光电技术应用,2014,29(4):13.

CHEN Kewei.PV Evaluation Standard Analysis of Mobile Phone Lens Aspheric Surface Accuracy[J].Electro-Optic Technology Application,2014,29(4):13.(in Chinese)

[8] 杨佳文,黄巧林,韩友民.Zernike多项式在拟合光学表面面形中的应用及仿真[J].航天返回与遥感,2010,31(5):49.

YANG Jiawen,HUANG Qiaolin,HAN Youmin.Application of Zernike Polynomials in Fitting Optical Surface and Its Simulation[J].Spacecraft Recovery & Remote Sensing,2010,31(5):49.(in Chinese)

[9] MAHAJAN V N.Zernike Circle Polynomials and Optical Aberrations of Systems with Circular Pupils[J].Applied Optics,1994,33(34):8121.

[10] WANG J Y,SILVA D E.Wave-front Interpretation with Zernike Polynomials[J].Applied Optics,1980,19(9):1510.

[11] QI B,DONG N.Regression Analysis for Wavefront Fitting with Zernike Polynomials[J].Proceedings of SPIE,2004,5180(3):429.

[12] 苏俊宏,田爱玲,杨利红,等.现代光学测试技术[M].北京:科学出版社,2013.

SU Junhong,TIAN Ailing,YANG Lihong,et al.Modern Optical Measurement Technology[M].Beijing:Science Press,2013.(in Chinese)