THE BOUNDS ABOUT THE WHEEL-WHEEL RAMSEY NUMBERS∗
Lili Shen,Xianzhang Wu
(College of Math.and Computer Science,Fuzhou University,Fuzhou 350116,Fujian,PR China)
1 Introduction
Throughout the paper,all graphs considered are undirected,finite and contain neither loops nor multiple edges.For given graphs G,H,the Ramsey number,denoted by R(G,H),is defined to be the smallest integer N such that in any edgecoloring of complete graph KNby colors red and blue,there exists either a red G or a blue H.A wheel Wmis a graph obtained from Cmand an additional vertex by joining it to every vertex of Cm.For a graph H and a vertex x∈H,define NH(x)as the subgraph induced by all vertices adjacent to x in H,and c(H),g(H)denote the lengths of a longest and shortest cycle of H.A graph H is called weakly pancyclic if it contains cycles of every length between g(H)and c(H).Letχ(H)be the chromatic number of H,that is,the smallest number needed to color the vertices of H so that no pair of adjacent vertices have the same color,andσ(H)be the size of the smallest color class among allproperχ(H)-colorings of H.
There is a famous lower bound of R(G,H)observed by Burr[3]as follows
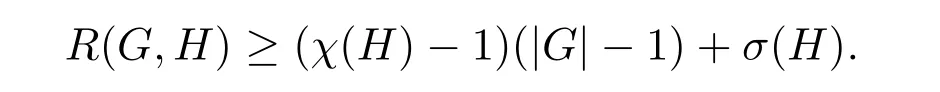
If R(G,H)is equal to this bound,we say that G is H-good.
For Ramsey numbers about wheels,Surahmat et al.[10]proved that Fnis W3-good for n≥3 where Fnconsists of n triangles sharing exactly one common vertex.Hendry calculated R(W3,W4)=17 in[7]and R(W4,W4)=15 in[8].Faudree and Mckay[6]proved the value of R(Wm,W5)for m=3,4,5,and R(W5,W3)=19.Yanbo Zhang et al.[12]obtained the exact value of R(Fn,Wm)for odd m≥3,n≥(5m+3)/4 and the exact value of R(Tn,Wm)for every ES-tree Tnodd m≥3,n≥m−2.Also[11]proved that
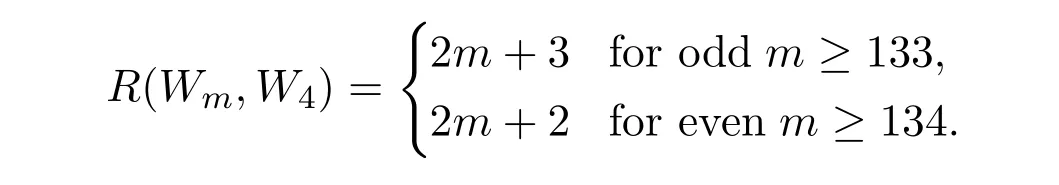
Motivated by the above works,in this paper,we shall consider the upper bound of the wheel-wheel Ramsey number R(Wm,Wn).The main results are as follows.
Theorem 1(i)Ifnis odd,m≥n≥3andm≥5,then
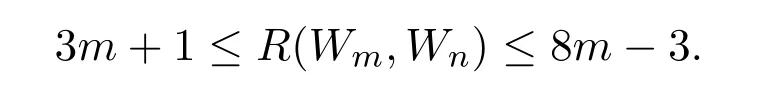
(ii)Ifnis even,m≥n+502,then
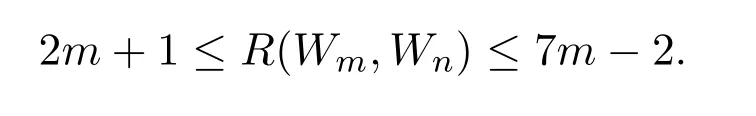
2 The Preliminary Lemmas
In order to establish the main results,we introduce some usefullemmas at first.
Lemma 1[4]Every nonbipartite graphGof ordernwithδ(G)≥ (n+2)/3is weakly pancyclic withg(G)=3or4.
Lemma 2[1]LetGbe a graph withδ(G)≥ 2.Thenc(G)≥ δ(G)+1.Moreover,ifδ(G)≥ |G|/2,thenGhas a Hamilton cycle.
Lemma 3[2]R(Wm,C3)=2m+1form≥5.
Lemma 4[5]R(Cm,Wn)=3m−2for oddn,m≥n≥3and(m,n)/=(3,3).
Lemma 5[13]R(Cm,Wn)=2m−1for evennandm≥n+502.
Lemma 6[9]For allp≥3,q≥1,0<γ<1,there existc>0,η>0such that ifnis large andE(Kp(n−1)+1)=E(R)∪E(B)is a2-coloring,then one of the following statements holds:
(i)RcontainsKp+1(1,1,t,···,t)fort= ⌈clogn⌉;
(ii)Bcontains everyq-degenerate,(γ,η)-splittable graphGof ordern.
We recall that a graph G is called q-degenerate if each of its subgraphs contains a vertex of degree at most q,that is,q=max{min{d(u),u ∈ V(G′)},G′∈ G}where G is the set of all subgraphs of G.For given real numbersγ,η >0,we say that the graph G of order n is(γ,η)-splittable if there exists a set S ⊆ V(G)with|S| It’s easy to see Wmis a 3-degenerate graph.Denote w by the center of the wheel Wm,and denote S to be the subset consisting of the vertex w and the other two vertices that have the largest distance from w.Then Wmis 3-degenerate,(1−log 4/log(m+1),1/2)-splittable graph of order m+1. Lemma 73m+1≤R(Wm,W3)≤5m−1form≥5.Especially,the lower bound equality holds formlarge enough. ProofThe lower bound can be obtained by whereχ(W3)=4,|Wm|=m+1 and σ(W3)=1.For the upper bound,let c be an arbitrary 2-edge coloring of K5m−1with colors red and blue,R and B denote the subgraphs of K5m−1induced by the red and the blue edges,respectively.By contradiction,suppose that R does not contain Wmand B does not contain W3. If d(u)=∆(B)≥2m+1,then,there is a C3in NB(u)by Lemma 3,which together with u forms a W3in B,a contradiction. If∆(B)≤ 2m,which means d(u)= δ(R)≥ (5m−1−1)− ∆(B)=3m−2,then by Lemma 4,we have R(Cm,W3)=3m−2.Thus,there exists a Cmin NR(u),which together with u forms a Wmin R,a contradiction. Especially,if m is large and E(K3m+1)=E(R)∪E(B)is a red/blue edge coloring,let p=3,q=3,γ=1−log 4/log(m+1),from Lemma 6,there exist c=1/log(m+1),η=1/2,such that either R contains K4=W3or B contains Wm.This completes the proof of Lemma 7. Proof of Theorem 1We first prove(i).The lower bound can be obtained by R(Wm,Wn)≥ (χ(Wn)−1)(|Wm|−1)+σ(Wn)=3m+1.For the upper bound,let c be an arbitrary 2-edge coloring of K8m−3with colors red and blue,R and B denote the subgraphs induced by the red and the blue edges,respectively.By contradiction,suppose that neither R contains a Wmnor B contains a Wn. If d(u)=∆(R)≥3m−2,then by Lemma 4,there is a Cmin NR(u),which together with u forms a Wmin R,a contradiction.Hence,d(u)=∆(R)≤3m−3,which implies d(u)=δ(B)≥(8m−3−1)−(3m−3)=5m−1≥R(Wm,W3).Then NB(u)contains a W3since R does not contain Wm.Now we choose a vertex v from W3,and let H=NB(v).Hence,we have|H|≥ δ(B)≥ 5m−1,g(H)=3 and H is nonbipartite. First,assumeδ(H)≥ (|H|+2)/3.Then by Lemma 1,H is weakly pancyclic.By Lemma 2,c(H)≥ δ(H)+1≥ (5m+4)/3>n.Thus H contains a Cn,which together with v forms a Wnin B,a contradiction. Next,assumeδ(H)≤ (|H|−1)/3,which implies that Let d(w)=∆,then by Lemma 4,there is a Cmin NR(w),which together with w forms a Wmin R,a contradiction.Thus,(i)follows. Now we prove(ii),the proof of which is similar to that of(i). The lower bound can be obtained by R(Wm,Wn)≥ (χ(Wn)− 1)(|Wm|− 1)+σ(Wn)=2m+1.For the upper bound,let c be an arbitrary 2-edge coloring of K7m−2with colors red and blue,R and B denote the subgraphs induced by the red and the blue edges,respectively.Suppose to the contrary that neither R contains a Wmnor B contains a Wn. If d(u)=∆(R)≥2m−1,then by Lemma 5 there is a Cmin NR(u),which together with u forms a Wmin R,a contradiction.Hence,d(u)=∆(R)≤2m−2,thus d(u)=δ(B)≥(7m−2−1)−(2m−2)=5m−1≥R(Wm,W3).Then NB(u)contains a W3since R does not contain Wm.Now we choose a vertex v from W3,and let H=NB(v).Hence,we have|H|≥δ(B)≥5m−1,g(H)=3 and H is nonbipartite. First,assumeδ(H)≥ (|H|+2)/3.Then by Lemma 1,H is weakly pancyclic.By Lemma 2,c(H)≥ δ(H)+1≥ (5m+4)/3>n.Thus H contains a Cn,which together with v forms a Wnin B,a contradiction. Next,assumeδ(H)≤ (|H|−1)/3,which implies that Let d(w)=∆then by Lemma 5,there is a Cmin NR(w),which together with w forms a Wmin R,a contradiction.Hence,(ii)follows. This completes the proof of Theorem 1. [1]G.A.Dirac,Some theorems on abstract graphs,Proc.Lond.Math.Soc.,2:1(1952),69-81. [2]S.A.Burr,P.Erdös,Generalizations ofa Ramsey-theoretic result of Chvátal,J.Graph Theory,7:1(2010),39-51. [3]S.A.Burr,Multicolor Ramsey numbers involving graphs with long suspended paths,Discrete Math.,40:1(1982),11-20. [4]S.Brandt,R.Faudree,W.Goddard,Weakly pancyclic graphs,J.Graph Theory,27(1998),141-176. [5]Y.Chen,T.C.E.Cheng,C.T.Ng,Y.Zhang,A theorem on cycle-wheelramsey number,Discrete Math.,312:5(2012),1059-1061. [6]R.J.Faudree,B.D.McKay,A conjecture of Erdös and the Ramsey numbers r(W6),J.Combin.Math.Combin.Comput.,13(1993),23-31. [7]G.R.T.Hendry,The Ramsey numbers r(K2+¯K3,K4)and r(K1+C4,K4),Util.Math.,35(1989),40-54. [8]G.R.T.Hendry,Ramsey numbers for graphs with five vertices,J.Graph Theory,13:2(1989),245-248. [9]V.Nikiforov,C.C.Rousseau,Ramsey goodness and beyond,Combinatorica,29:2(2009),227-262. [10]Surahmat,E.T.Baskoro,H.J.Broersma,The Ramsey numbers offans versus K4,Bull.Inst.Combin.Appl.,43(2005),96-102. [11]Y.Zhang,Some new Ramsey-type results in graph theory,unpublished PhD dissertation,Nanjing University,2016. [12]Y.Zhang,H.Broersma,Y.Chen,On fan-wheeland tree-wheel Ramsey numbers,Discrete Math.,339(2016),2284-2287. [13]Y.Zhang,H.Broersma,Y.Chen,Three results on cycle-wheel Ramsey numbers,Graphs Combin.,31:6(2015),1-13.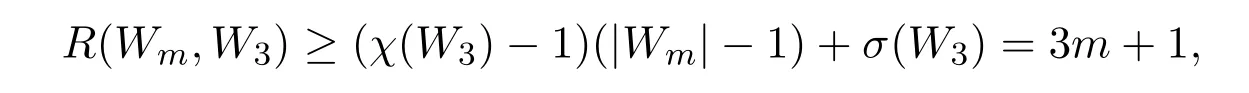
3 Proof of the Main Result
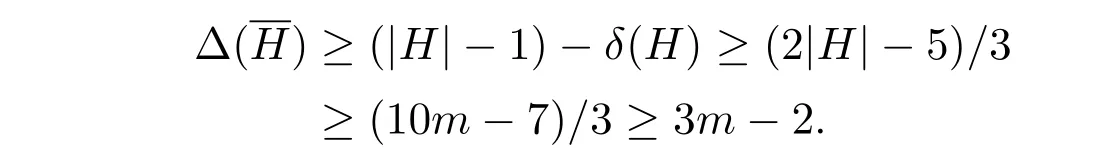
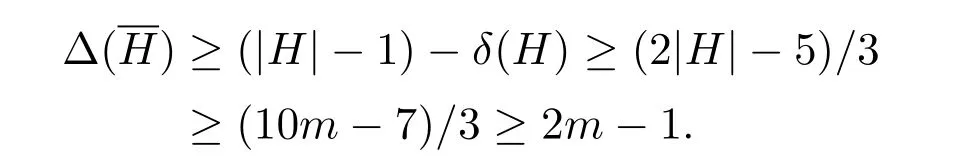
 Annals of Applied Mathematics2018年2期
Annals of Applied Mathematics2018年2期
- Annals of Applied Mathematics的其它文章
- DYNAMICS OF A PREDATOR-PREY REACTION-DIFFUSION SYSTEM WITH NON-MONOTONIC FUNCTIONAL RESPONSE FUNCTION∗†
- DYNAMICAL ANALYSIS OF A SINGLE-SPECIES POPULATION MODEL WITH MIGRATIONS AND HARVEST BETWEEN PATCHES∗†
- NEWDYNAMICINEQUALITIES FORDECREASING FUNCTIONS AND THEOREMS OF HIGHER INTEGRABILITY∗
- A COMMENSAL SYMBIOSIS MODEL WITH HOLLING TYPE FUNCTIONAL RESPONSE AND NON-SELECTIVE HARVESTING IN A PARTIAL CLOSURE∗†
- A BLOCK-COORDINATE DESCENT METHOD FOR LINEARLY CONSTRAINED MINIMIZATION PROBLEM∗†
- ESTIMATION OF PARAMETERS IN A CLOSED PYGMY POPULATION IN CAMEROON∗†
