A BLOCK-COORDINATE DESCENT METHOD FOR LINEARLY CONSTRAINED MINIMIZATION PROBLEM∗†
Xuefang Liu,Zheng Peng
(College of Math.and Computer Science,Fuzhou University,Fuzhou 350116,Fujian,PR China)
1 Introduction
We consider in this paper a linearly constrained convex optimization problem of the form:

whereh(x)is a proper,convex and lower semi-continuous(lsc)function,A∈Rm×nandb∈Rm.In this paper,we assume that the objective functionh(x)has a(block)-separable form,that is,wherexsis thes-th block of the decision variablexandhsis proper,convex and lower semi-continuous.
Problem(1.1)is very general which generalizes the constrained minimum distance sum problem,where the Euclidean distance,l1norm distance orl∞norm distance can be selected.It has widely applications in business,industry areas,facility location,integrated circuits placement and so on.
The coordinate gradient descent method has been used in many considerable discussions,see for example Fukushima[4].Tseng and Yun[13]gave a coordinate gradient descent method with an Armijo-type line search under an assumption thathis a separable and smooth function.Bai,Ng and Qi[8]showed that the gradient based methods cannot be employed directly to solve problem(1.1)whenh(x)is nonsmooth.In addition,problem(1.1)has also raised in many applications,including signal denosing,image processing and data classification.In this case,those methods updating one coordinate variable at each iteration have been well suited due to their low computational cost and easy implementation[6].For example,the(block-)successive over-relaxation(SOR)method is used to find sparse representation of signals,and some decomposition methods are used to support vector machine(SVM)training,etc.
The block coordinate descent(BCD)method divides the variablexinto a few small blocks,then minimizes at each iteration the objective function with respect to one-block of the variable by fixing the other blocks.The BCD method can be found under numerous names,including linear or nonlinear Gauss-Seidel method,subspace correction method and alternating minimization approaches.Since the dimension of each block is often small,the computational cost of each iteration is relatively cheap which is suitable for large scale problem.
The blocks of the variable are often updated by using several types of strategies in the BCD method.The cyclic(Gauss-seidel)strategy updates blocks one by one in turn and the values of the newly updated blocks are used in the subsequent operations on the other blocks.The essentially cyclic rule selects each block at least once every successiveTiterations,whereTis an integer not less than the number of blocks.The Gauss-Southwell rule computes a positive valueqsfor thes-th block according to some criteria,and then chooses the block with the largest value ofqsto work on next,or chooses thek-th block to work on,whereqk≥β×forβ∈(0,1].Recently,some randomized rules have been proposed by Zhao[16],Nesterov[7]and Richtrik[10],etc.The greedy coordinate block descent method[14]selected a few blocks of the variable and a few variables in each selected block,by greedy means,and updated the latter in parallel fashion at each iteration.The Jacobian-type iteration updated all the blocks simultaneously,hence it is suitable for parallel computation and distributed optimization[2,3].
In this paper,the BCD method for the unconstrained composite optimization pro-posed by Dong,Liu and Wen[5]is extended to the linearly constrained optimization problem(1.1),and the global convergence of the extended BCD method is proved.Some preliminary numerical results show that the proposed method is effective.
The paper is organized as follows.In Section 2,the extended BCD method using the cyclic rule is proposed,and all the subproblem solvers are also given in this section.In Section 3,the convergence analysis of the extended BCD method is derived.In Section 4,some implementation issues are described,and some preliminary numerical results are reported.In Section 5,the final remarks are presented to conclude this paper.
2 Block Coordinate Descent Method
Suppose that the variablexis split intopblocks,namelywherexs∈the equality holds if and only if there is not overlapping in this splitting strategy.Correspondingly,the matrixAis also split intopblocks,that is,A=[A1,···,As,···,Ap].Then,the BCD method to solve(1.1)can be formally described as follows.

It is known that the minimum of subproblem(2.1)is attainable if the level setX0:={x:h(x)≤h(x0)}is bounded andhis lsc onX0.To ensure convergence,each block has to be chosen sufficiently frequent in the BCD method.In particular,we choose blocks according to the so-called “Essentially Cyclic Rule”.There exists a constantT≥psuch that for allk>0,each indexs∈{1,···,p}is chosen at least one time between thek-th iteration and the(k+T−1)-th iteration.As a special case,ifT=p,then this rule chooses thes-block at the iterationsk,k+p,k+2p,···,see Tseng[11],Tseng and Yun[12].
Each subproblem of the BCD method is a linear inequality constrained optimization problem,we adapt the augmented Lagrangian method[15]for these sub-problems.Denote the matrixAremoved the partAsby,the vectorxremoved the partxsby.Then subproblem(2.1)is as follows:
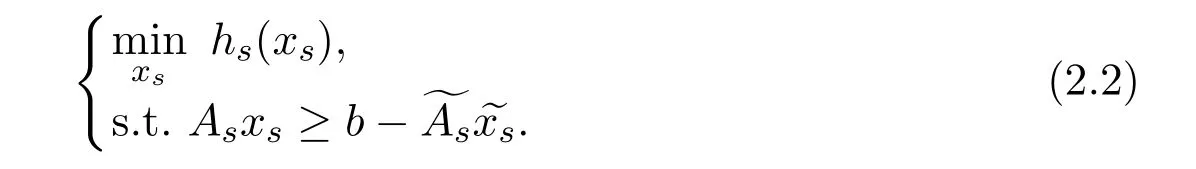
Denote the right-handin the constraint of(2.2)byand adding an auxiliary variabley∈to the inequality constraint of this subproblem,we get
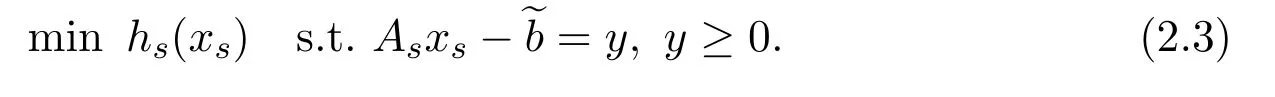
The augmented Lagrangian function associated to problem(2.3)is
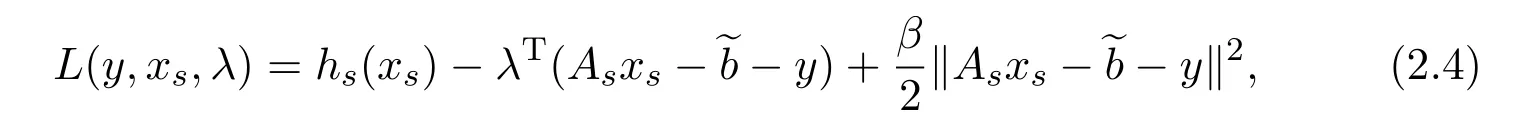
whereλ∈Rmis a Lagrange multiplier andβ>0 is a penalty parameter.It is well known that,starting fromλ0,the classical augmented Lagrangian method minimizes
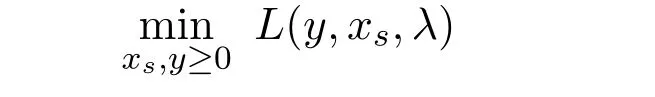
at the current iteration,then updates the multiplierλsubsequently.However,minimizingL(y,xs,λ)with respect toxsandysimultaneously is usually difficult,while separately minimizingL(y,xs,λ)with respect toxsandycould be very efficient.Hence,the following alternating direction version of the augmented Lagrangian method(ALM for short)is frequently advocated:
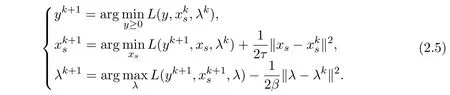
Due to they’s subproblem of iteration(2.5),with fixedxs=andλ=λk,we get
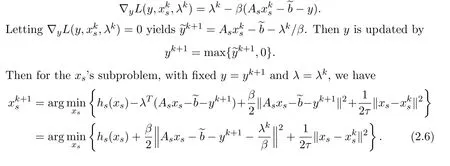
It is still difficult to solve(2.6)directly.It is desirable to find an approximate solution of this subproblem which is globally convergent.Define
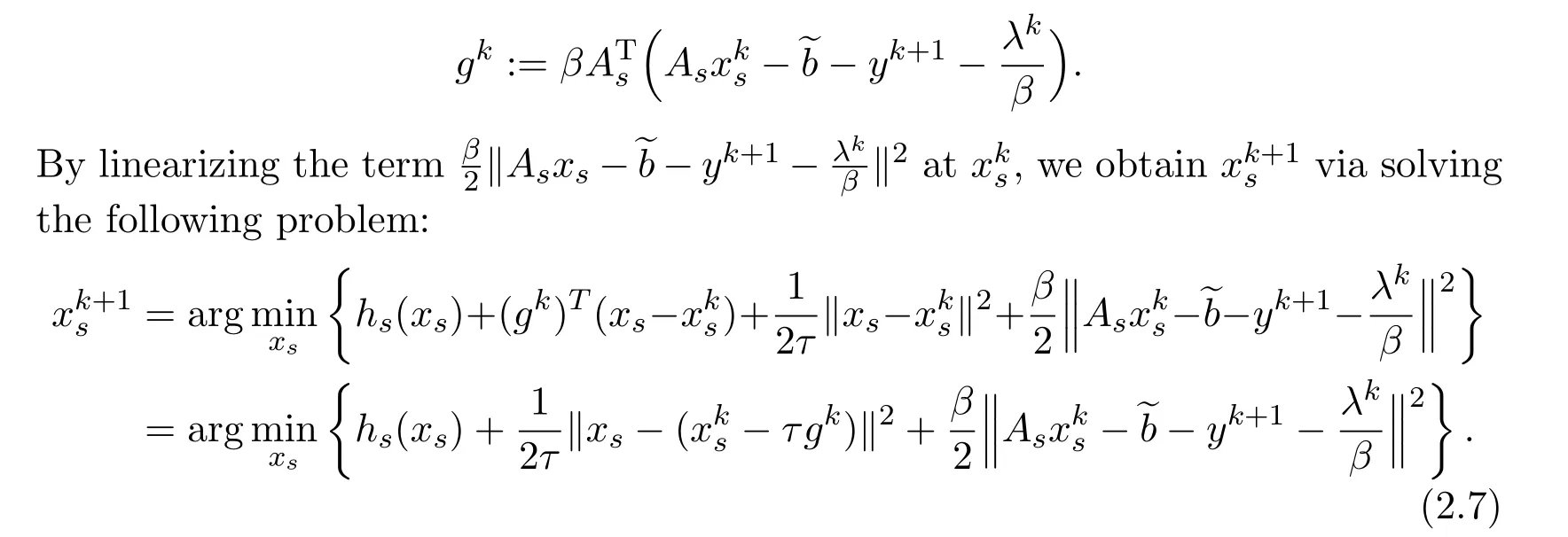
The Lagrangian multiplier is finally updated by
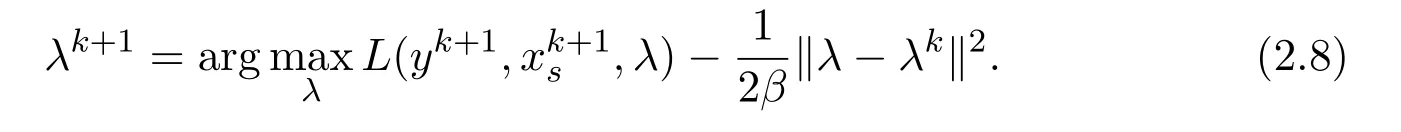
3 Convergence Analysis
The Lagrangian function of problem(2.2)(without the penalty termis
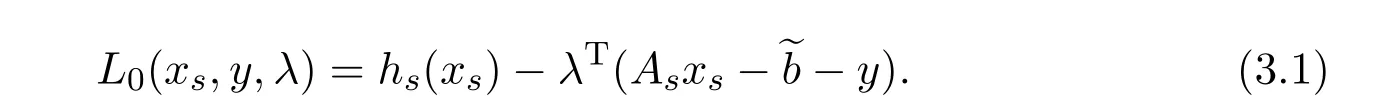
The augmented Lagrangian function(2.4)can be viewed as the Lagrangian associated to the problem
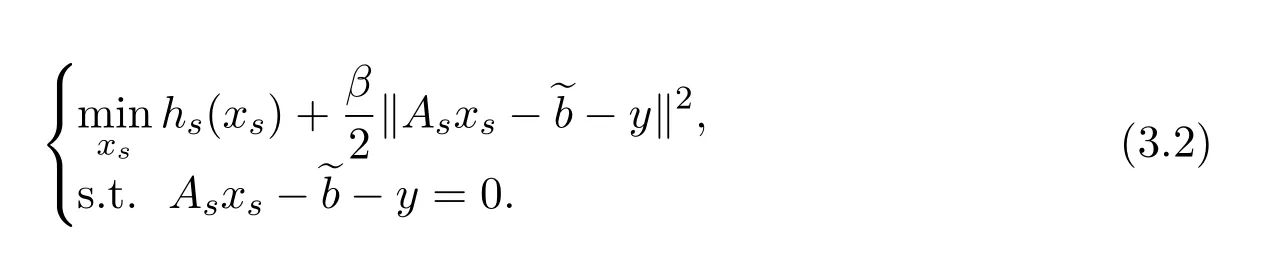
For regularity,the following assumptions on the subproblems are needed:
A.The solution set of(2.3),denoted by,is not empty,and the LICQ condition holds at the point(,y∗)∈.
B.For alls=1,2,···,p,the functionhsis Lipschitz continuously differentiable.That is,there exists a constantL>0 such thatfor anyx,y∈Rn,
C.All matricesAsare row full rank,s=1,2,···,p.
By these assumptions,there is a threshold value of the penalty parameter=0 such that,for allβ>the pair(,y∗)is a stationary point of the augmented Lagrangian functionLβ(y,xs,λ)withλ=λ∗,see Nocedal and Wright[9],Peng[1].
By the first-order conditions of optimality,the pair(,y∗)is a critical point of the constrained minimization problem(2.3)if there exists aλ∗∈Rmsuch that
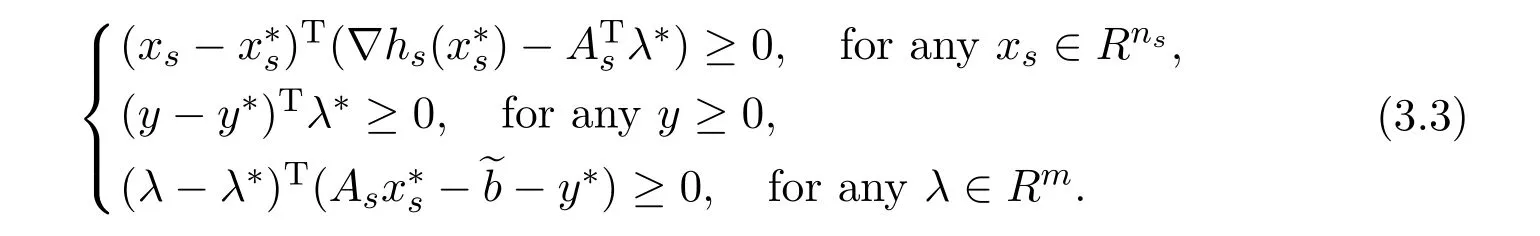
By the convexity of they’s subproblem in(2.5),we have
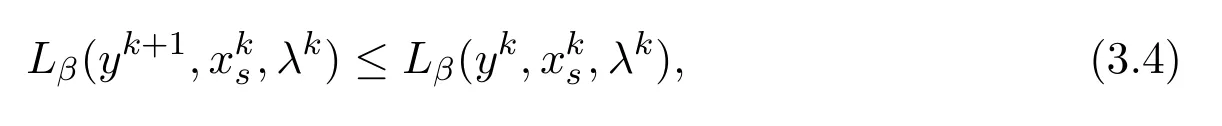
and by(2.7)there is
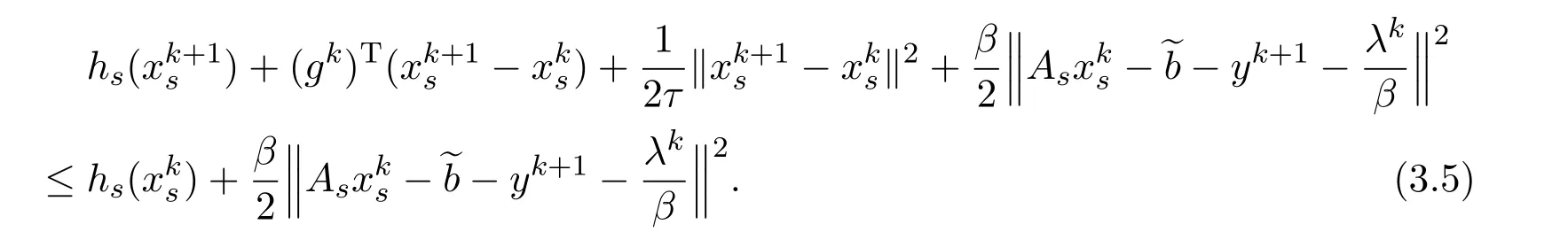
Using Taylor’s theorem,we get
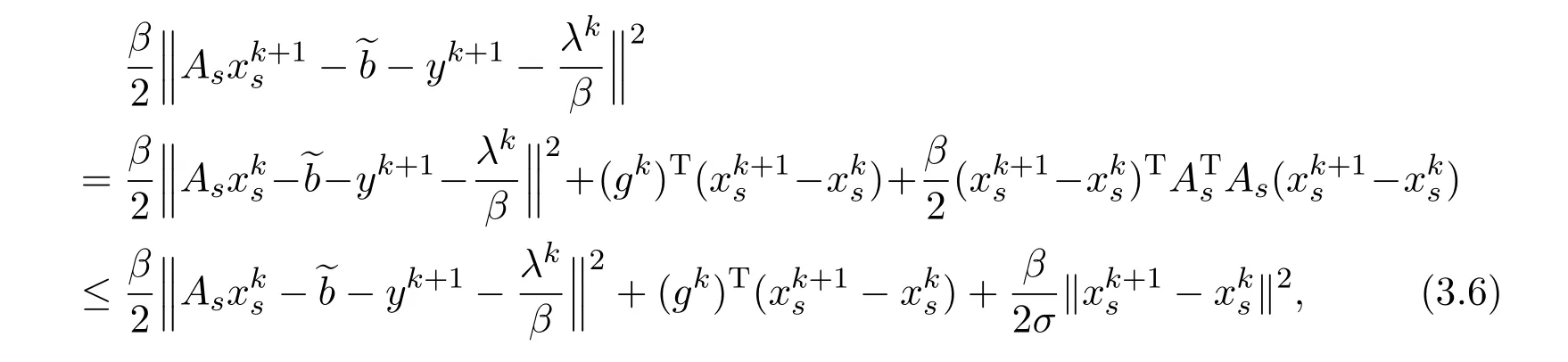
whereσ−1is the maximal eigenvalue of the matrixAs.Combing this with(3.5),we obtain
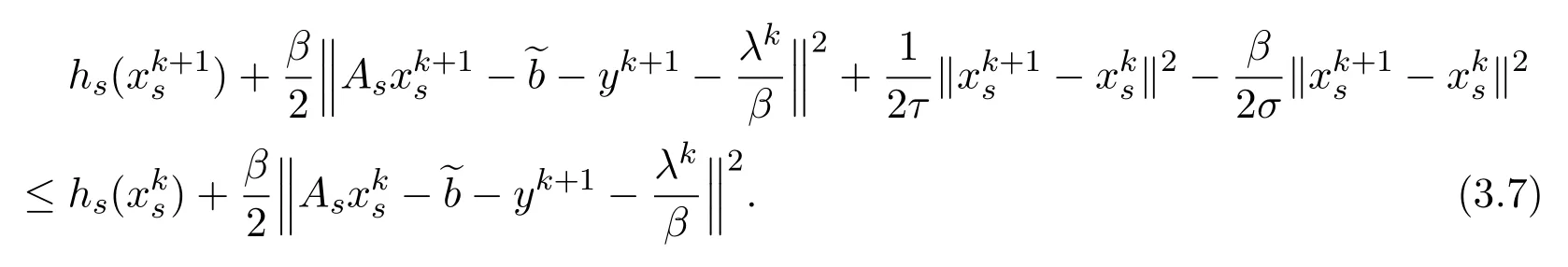
By a selection of the proximal parameterτ>0 such that>0,we have
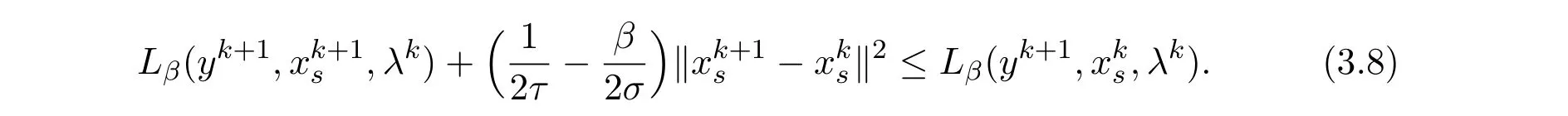
Adding(3.4)and(3.8)yields
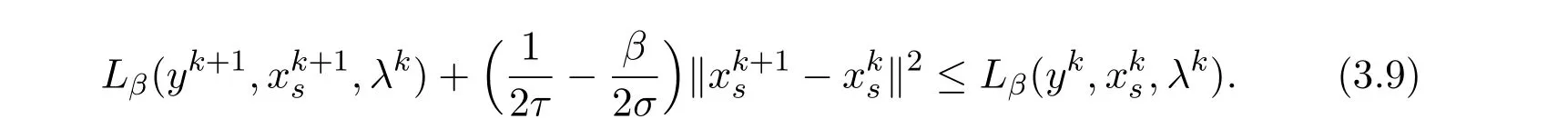
Inequality(3.9)implies that the scheme(2.5)is primal descent provided with the suitable choice of the parametersτandβ.
Denotethen by the first-order condition of optimality of(2.7),we have
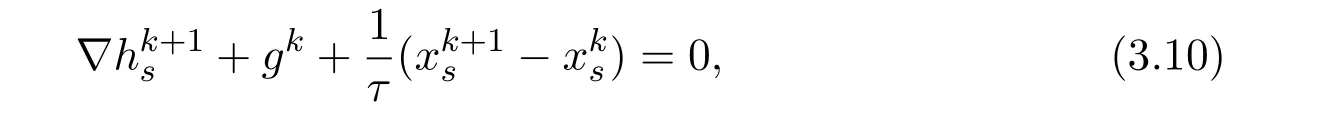
where
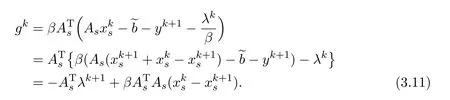
Substituting(3.11)into(3.10)yields
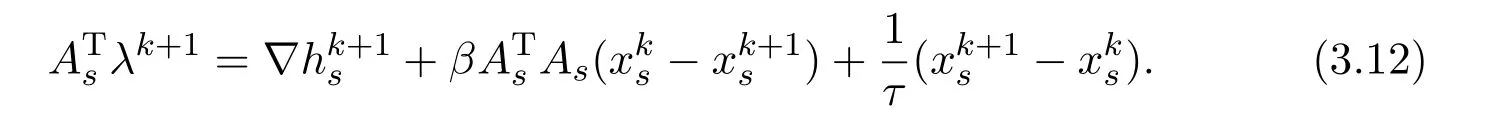
At thek−1 iteration,it is
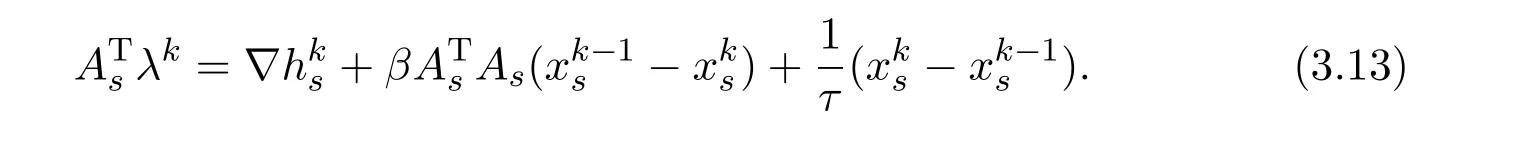
Hence

Lemma 3.1Suppose that the sequenceis generated by the scheme(2.5),and assumptionsBandChold.Then there exist constants r1and r2such that
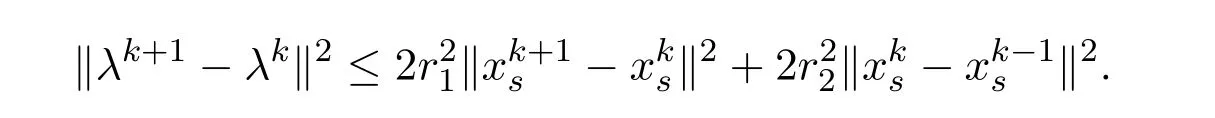
ProofTaking norm on both sides of(3.14),by the Cauchy-Schwarz inequality and the triangle inequality,we get
By assumption C,there exists a realρ>0 such that
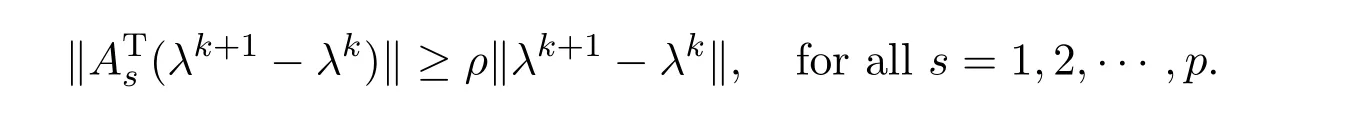
Thus,by assumption B,we have
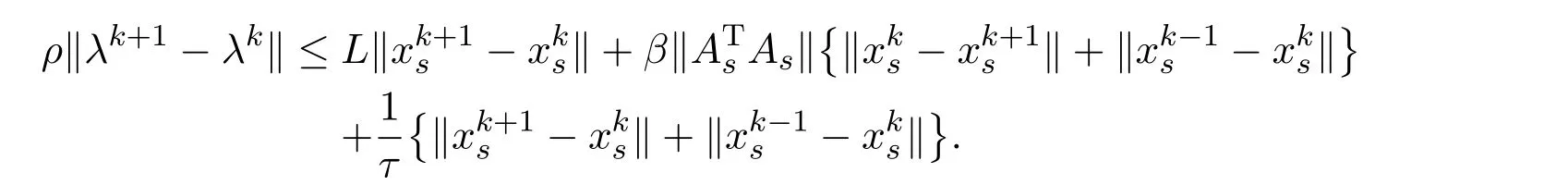
Hence
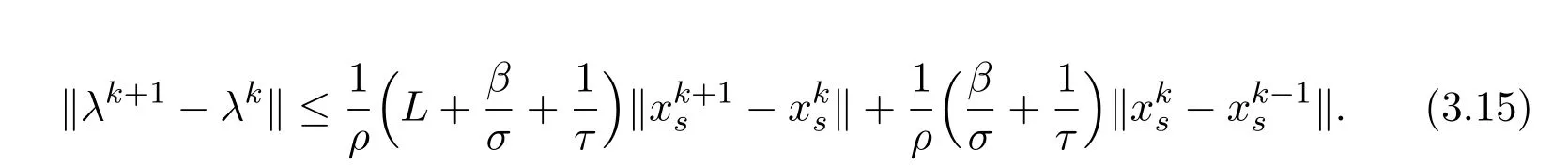
Letr1then by 2a2+2b2≥(a+b)2we have the assertion of the lemma,which completes the proof.
Lemma 3.2Suppose that the sequenceis generated by the scheme(2.5),and assumptionsA,BandChold.By a suitable choice of the parametersτandβ we have
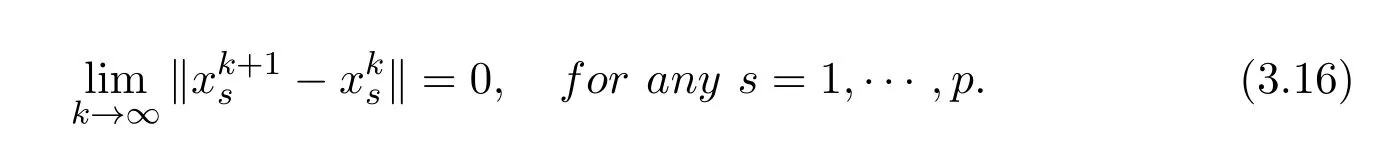
ProofBy primal descent property of the scheme(2.5)we have(3.9).That is,

By the boundedness ofLβ(xs,y,λ),there exists a constantCsuch that
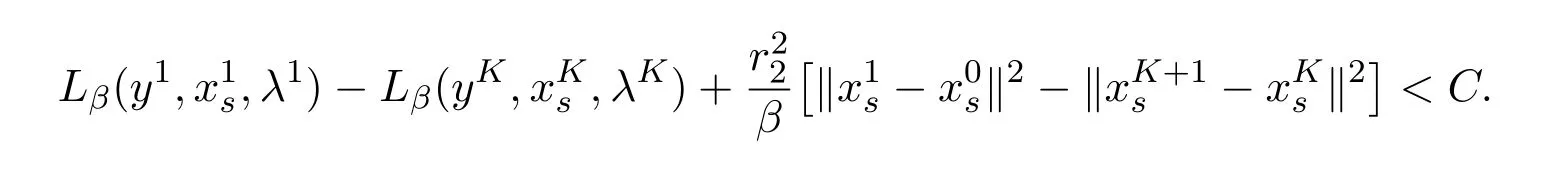
By the suitable choice ofτandβsuch that
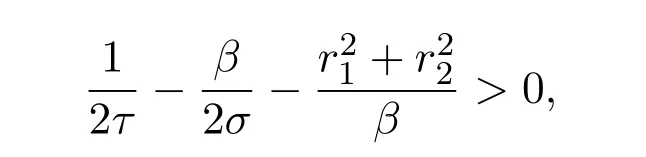
and taking limits on both sides of(3.22)asK→∞,we have(3.16)and this completes the proof.
Lemma 3.3Suppose that assumptionsAandBhold,and the sequence{λk}is generated by(2.8).Then we have
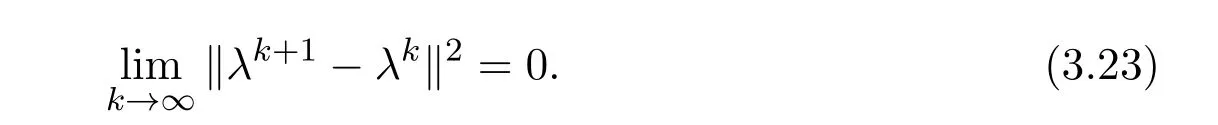
ProofBy Lemmas 3.1 and 3.2,the assertion can be immediately derived.
According to the above discussion,we have that the sequence{(,y k,λk)}is bounded.Thus,by Weierstrass theorem it admits an accumulation point.That is,there exists a convergent subsequence{(yk,λk)}k∈K,whereK⊂{1,2,···}.For convenience,denote

We prove the convergence of the BCD method by verifying that the accumulation point(,y∞,λ∞)of the convergent subsequence{(,yk,λk)}k∈Kis a critical point of the problem under considered.For simplification,the notationis used to denote
Theorem 3.1Suppose that the sequence{,yk}is generated by the scheme(2.5)and assumptionsA,BandChold.Then the primal residual satisfies
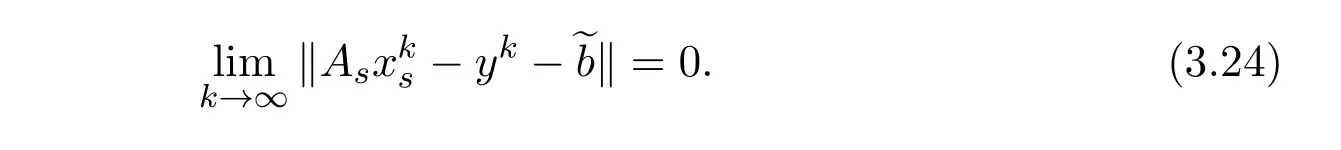
ProofThe assertion can be immediately derived from Lemma 3.3,and it provides the primal feasibility of the iterate{,yk}at the limit.
Theorem 3.2Suppose that the sequence{,yk,λk}is generated by the BCD method,and assumptionsAandBhold.Then,
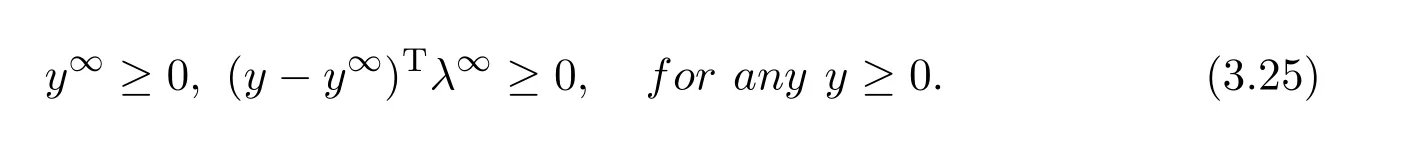
ProofIt follows from Lemma 3.2 that

Sinceyk+1solves they-subproblem of scheme(2.5),we get
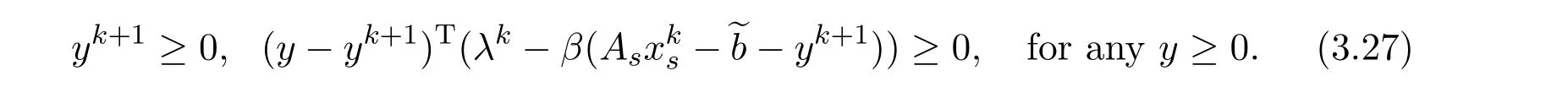
Thus
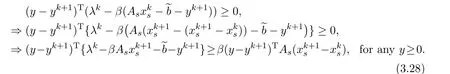
Substitutingλk+1=into the last inequality,we have

Taking limits on both sides of(3.29)and using(3.26),we get(3.25),and complete the proof.
Theorem 3.3Suppose that the sequence{,yk,λk}is generated by the scheme(2.5),and assumptionsAandBhold.Then,for any xs∈Rns,we have
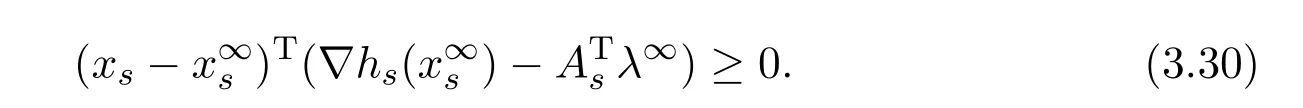
ProofSincesolves thex-subproblem,we have
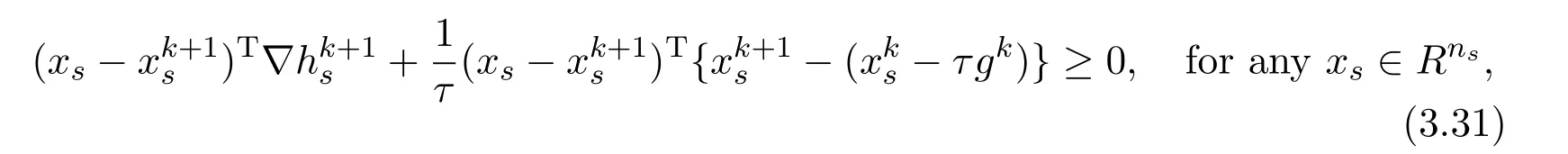
which deduces
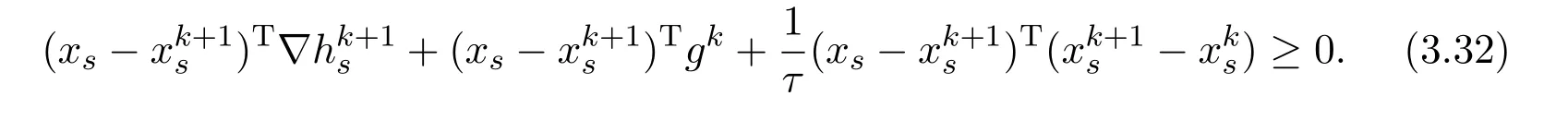
Then

Substituting(3.11)into(3.33),we obtain
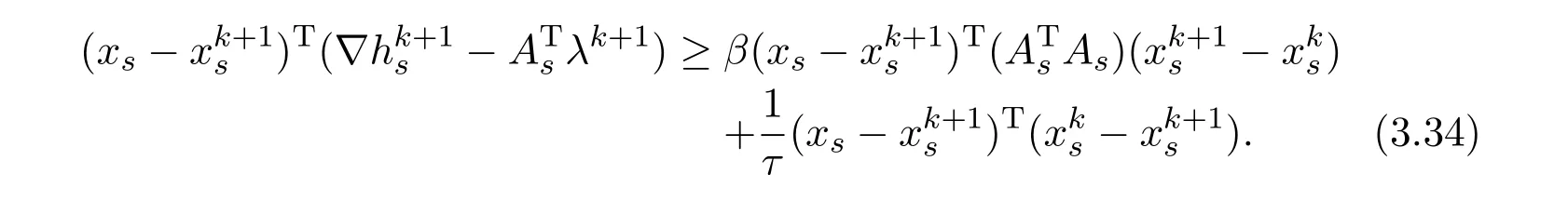
Taking limits on both sides of(3.34),by Lemma 3.2 we get(3.30).The proof is completed.
Up to now,we have checked that,the accumulation point(,y∞,λ∞)of the convergent subsequence{(,yk,λk)}k∈Kgenerated by the scheme(2.5)satisfies conditions(3.3).Hence it is a critical point of problem(2.2).Since this problem is a convex optimization,the accumulation point(,y∞,λ∞)is also a global minimizer of problem(2.2).
Lemma 3.4For a given?k>0,each subproblem of the BCD method can beterminated with
ProofSince the subproblem of each iteration only updates thes-th block,we0.
Theorem 3.4By the cyclic rule,the sequence{xk}generated by the proposed BCD method is convergent to a critical point of problem(1.1).
ProofIn each subproblem,we get
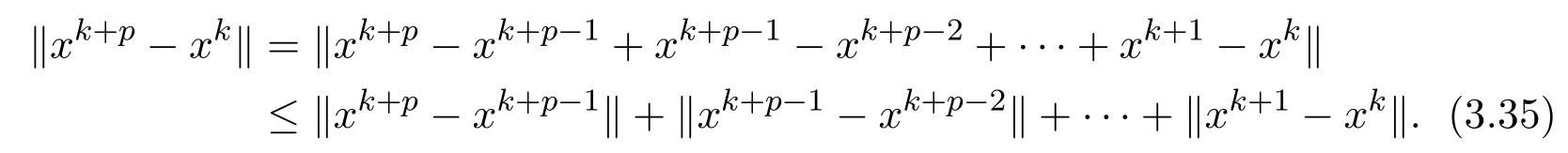
Letting?k<(for anyk)for arbitrarily given?>0,we getp×=?,which implies that the sequence{xk}generated by the BCD method is asymptotically regular.It is easy to prove that any regular sequence generated by the BCD method converges to a critical point of problem(1.1).
4 Numerical Implementation
In this section,we demonstrate the validity and efficiency of the proposed method on the following problem:

whereA∈Rm×nandb∈Rm.Four implementations of the BCD method are used,they are:the BCD method within augmented Lagrangian scheme for non-overlapping case(BCD-ALMN),the BCD method within augmented Lagrangian scheme for overlapping case(BCD-ALMO),the BCD method within CVX scheme for nonoverlapping case(BCD-CVXN),and the BCD method within CVX scheme for overlapping case(BCD-CVXO).We compare the BCD method with the “full-type”method.
The potential of the BCD method is further illustrated in some large scale problems.All the implementable methods used in these numerical experiments are coded in MATLAB 2016a and run on a personal computer Lenovo with 2.0GHz AMD A8-6410 APU and 4GB RAM.
Algorithmic Issues of BCDThe non-overlapping domain decomposition scheme is designed as the same method proposed by Dong,Liu and Wen[5].Suppose that the variablesx∈Rnare divided into blocks as
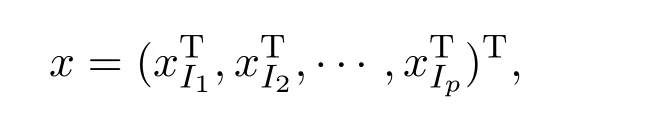
wherexIcontains the components ofxcorresponding to the index setI.Similarly,the matrixAis also split by columns according to the division ofx,that is,
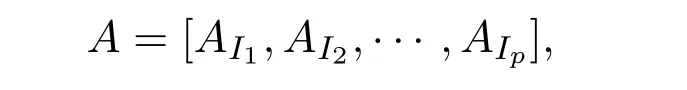
whereAIcontains the columns ofAcorresponding to the index setI.The subsets areI1,···,Ipare chosen to have the same size.
By using the above scheme,we splitIsinto three partsIls,IcsandIrsby the order of coordinates.Then a new subsetof coordinates is constructed fromIrs−1,IsandIls+1.More specifically,we have
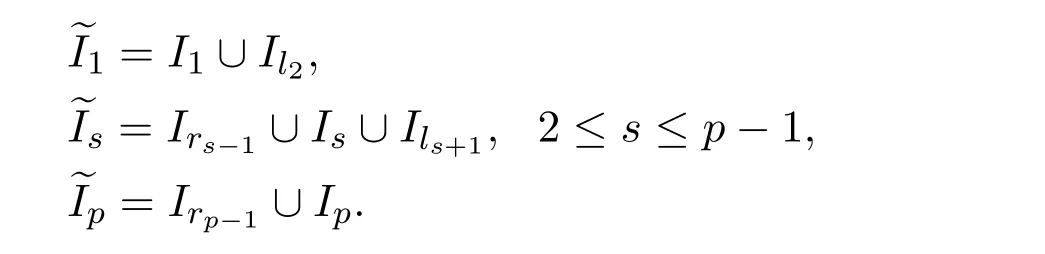
Consequently,two immediately adjacent blocks have a overlapping part,which is denoted byOs=Irs∪Ils+1,1≤s≤p−1.The overlapping regionsOs(1≤s≤p−1)have the same size.WhenOs=∅(for alls),it reduces to the non-overlapping case.An example of the overlapping domain decomposition is shown in Figure 1.
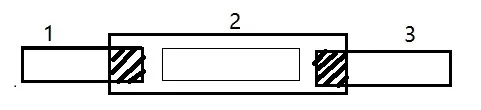
Figure 1:The overlapping domain decomposition structure
Data PreparationIn our numerical experiments,the data matrixAand exact solutionx∗are generated randomly,then the right-hand-sidebis generated by the method used in Peng,Yan and Yin[14].The detailed information of the data sets is described in Table 1.Note that there are two types of data sets in Table 1.For data sets I,III,V and VII,matrixAis generated randomly.For data sets II,IV,VI and VIII,the columns ofAare designed to have a special overlapping structure,for example,matrixAin data set II is divided into 4 blocks that each immediately adjacent pair of blocks have 20 overlapping columns.
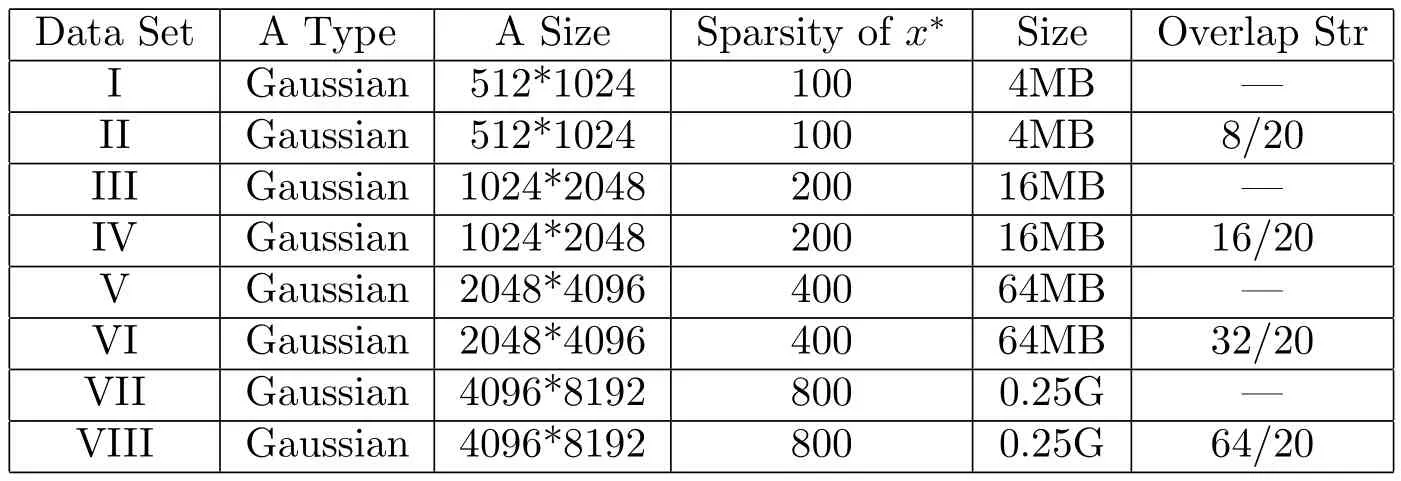
Table 1:Test data sets for problem(1.1)
The initial point is set to bex0=0.All algorithms are terminated whenever the stopping criterion
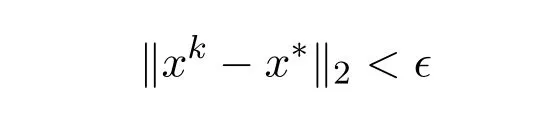
is met with?=10−4.The size of the overlapping blocks between two immediately adjacent blocks is set by the same pattern as that of matrixA.
In what follows,we solve a series of random examples with different size of block.Table 2 lists the computation time(cput)of BCD-CVX method under different blocking strategies.

Table 2:Numerical results of BCD-CVX method under different blocking strategies

Figure 2:The different strategies correspond to different times
The above test results suggest that,when the size of one block locates in 100 to 150,the computing time may be shorter.So in the following experiments,the size of each block is set around 120.
Numerical Comparisons on the BCD method and the “full-type”methodWe compare the numerical performance of four implementations of the BCD method:BCD-ALMN,BCD-ALMO,BCD-CVXN,and BCD-CVX,with that of the “full-type” CVX method,on the above data sets.The number of iterations and CPU time are list in Table 3 for comparison.For the “full-type”CVX method,we only list“CPU time”in Table 3.The notation “N”and “O”mean the data sets with non-overlapping and one of that with overlapping,respectively.
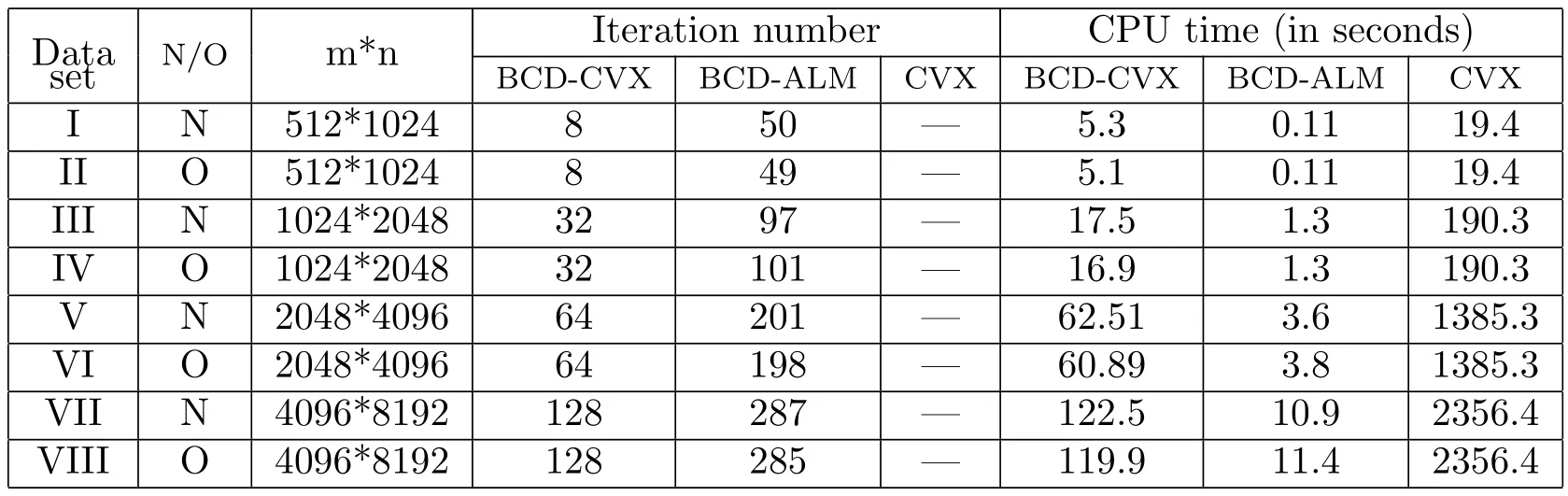
Table 3:Comparisons of the BCD method with the “full-type” CVX method
The number of iteration is related to the number of blocks in both BCD-ALM and BCD-CVX.The BCD-ALM method iteratively solves the subproblems,while the BCD-CVX method uses CVX toolbox as the subproblem solver,the number of iterations of the BCD-ALM method is more than that of the BCD-CVX method on the same data set.
Table 3 shows that,the “full-type” CVX method is faster than BCD-CVX method on the low-dimension data sets I and II.For the high-dimension data sets III,IV,V and VI,the BCD-CVX method is much faster than the “full-type” CVX method.
5 Conclusion
The coordinate descent methods are simple and effective algorithms for solving general convex problems.As well as,the block coordinate descent can solve the separable convex optimization problem more quickly.In this paper,we extend the block coordinate descent method to the linear constrained separable minimization.Our approaches are motivated by the typical structure of sparse optimization problem.Four implementable versions of the BCD method are presented depending on whether there are overlapping between two or more immediately adjacent blocks.Numerical results show that the proposed method is effective than the “full-type”method.Meanwhile,the non-overlapping versions are slightly better than the overlapping versions in many cases.
[1]Z.Peng,J.Chen,and W.Zhu,A proximal alternating direction method of multipliers for a minimization problem with nonconvex constraints,Journal of Global Optimization,62:4(2015),711-728.
[2]O.Fercoq and P.Richtrik,Smooth minimization of nonsmooth functions with parallel coordinate descent methods,Mathematics,27:4(2013),178-180.
[3]O.Fercoq and P.Richtrik,Accelerated,parallel and proximal coordinate descent,SIAM Journal on Optimization,25:4(2015),1997-2023.
[4]M.Fukushima,A successive quadratic programming method for a class of constrained nonsmooth optimization problems,Mathematical Programming,49:1(1990),231-251.
[5]Q.Dong,X.Liu,and Z.Wen,A parallel line search subspace correction method for composite convex optimization,Journal of the Operations Research Society of China,3:2(2015),163-187.
[6]I.Necoara and D.Clipici,Efficient parallel coordinate descent algorithm for convex optimization problems with separable constraints:application to distributed mpc,Journal of Process Control,23:3(2013),243-253.
[7]Y.Nesterov,Efficiency of coordinate descent methods on huge-scale optimization problems,SIAM Journal on Optimization,22:2(2012),341-362.
[8]Z.Bai,M.Ng,and L.Qi,A coordinate gradient descent method for nonsmooth nonseparable minimization,Numerical Mathematics Theory Methods and Applications,4(2009),377-402.
[9]J.Nocedal and S.J.Wright,Numerical Optimization,Springer,New York,2006.
[10]P.Richtrik and M.Tak,Iteration complexity of randomized block-coordinate descent methods for minimizing a composite function,Mathematical Programming,144:1-2(2014),1-38.
[11]P.Tseng,Convergence of a block coordinate descent method for nondifferentiable minimization,Journal of Optimization Theory and Applications,109:3(2001),475-494.
[12]P.Tseng and S.Yun,Block-coordinate gradient descent method for linearly constrained nonsmooth separable optimization,Journal of Optimization Theory and Applications,140:3(2009),513-535.
[13]P.Tseng and S.Yun,A coordinate gradient descent method for nonsmooth separable minimization,Mathematical Programming,117:1(2009),387-423.
[14]Z.Peng,M.Yan,and W.Yin,Parallel and distributed sparse optimization,Signals,Systems and Computers,2013 Asilomar Conference on,pages 659-646,2013.
[15]Z.Wen,W.Yin,and D.Goldfarb,A fast algorithm for sparse reconstruction based on shrinkage,subspace optimization,and continuation,SIAM Journal on Scientific Computing,32:4(2010),1832-1857.
[16]T.Zhao,M.Yu,and Y.Wang,Accelerated mini-batch randomized block coordinate descent method,Advances in neural information processing systems,27(2014),3329-3337.
 Annals of Applied Mathematics2018年2期
Annals of Applied Mathematics2018年2期
- Annals of Applied Mathematics的其它文章
- DYNAMICS OF A PREDATOR-PREY REACTION-DIFFUSION SYSTEM WITH NON-MONOTONIC FUNCTIONAL RESPONSE FUNCTION∗†
- DYNAMICAL ANALYSIS OF A SINGLE-SPECIES POPULATION MODEL WITH MIGRATIONS AND HARVEST BETWEEN PATCHES∗†
- THE BOUNDS ABOUT THE WHEEL-WHEEL RAMSEY NUMBERS∗
- NEWDYNAMICINEQUALITIES FORDECREASING FUNCTIONS AND THEOREMS OF HIGHER INTEGRABILITY∗
- A COMMENSAL SYMBIOSIS MODEL WITH HOLLING TYPE FUNCTIONAL RESPONSE AND NON-SELECTIVE HARVESTING IN A PARTIAL CLOSURE∗†
- ESTIMATION OF PARAMETERS IN A CLOSED PYGMY POPULATION IN CAMEROON∗†
