基于动力某钢管混凝土系杆拱桥有限元模型修正静载试验分析

■ 郑景祥

（1.福建省建筑科学研究院，2.福建省绿色建筑技术重点实验室，福州 350025）

1 桥梁概况

某钢管混凝土拱桥[1-2]桥跨布置由西向东为：3×20m的预应力混凝土空心板+80m下承式钢管混凝土系杆拱+3×20m的预应力混凝土空心板，桥梁总长216m。空心板3跨一联，桥面连续，全桥设伸缩缝四道。上部结构主跨为墩中心距80m的钢管混凝土下承式系杆拱，净跨径75m，净矢跨比1/5，净矢高15m。拱肋采用直径Φ1200mm的钢管，拱脚段管壁厚16mm，内填C40混凝土，拱顶段管壁厚20mm，为空钢管，两肋之间设两根一字式横撑。桥面宽度：净-12+2×2m人行道。桥面纵坡为2%。设计荷载：汽车-20级，挂车-100级，人群荷载3.5kN/m2。

2 基于动力的有限元模型修正

2.1 基于动力有限元模型修正函数的确立

为了使目标函数最优化，目标函数的构造主要利用测试值与计算值的差值。在基于动力测试数据的有限元模型修正中，将频率、MAC和模态柔度三个目标函数联合起来，可以构造如下的目标函数[3-5]，

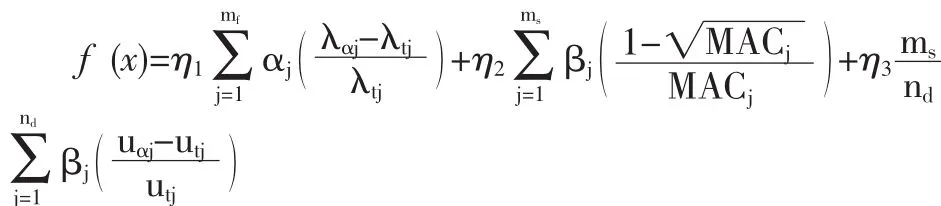
式中：f（x）为中联合频率、MAC、模态柔度的目标函数；αj为权重系数；βj为权重系数；λαj为 j阶理论特征圆频率；λtj为j阶试验特征圆频率；MACj为第j阶的模态保证准则值；uαj为理论的一致荷载面；utj为试验的一致荷载面；ms为测试的自由度；nd为测试的模态阶数；[Φik]为质量归一的振型矩阵；（k=1，2…，n）为固有频率；UL 为理论与试验值特征值之间误差的上限；L1为MAC的下限；η1、η2、η3为权重系数，η1、η2、η3权重系数的分配根据不同目

标函数对结构灵敏度不同进行分配。

2.2 环境振动测试

（1）测点布置

在行车道边缘沿着吊杆位置布置加速度传感器，测点布置详见图1。本次试验采样频率为100Hz，采样时间为20min。

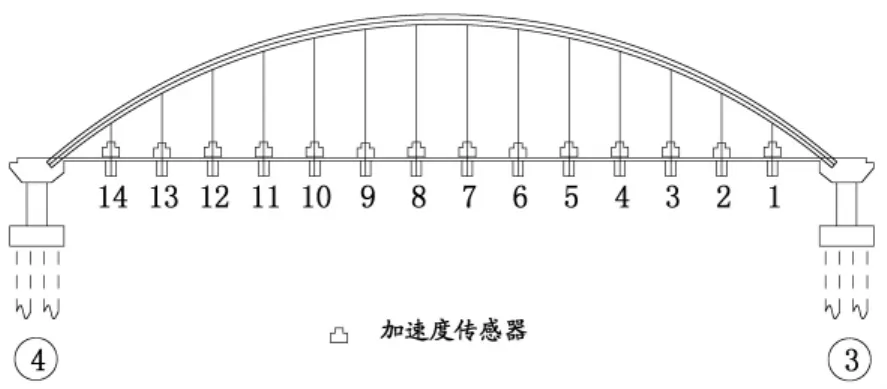
图1 环境振动传感器测点布置示意图

（2）试验结果与分析

实测信号经模态分析，得到桥梁竖向振动频率，数据表明，桥梁实测基频大于桥梁实测基频，且大于有限元理论计算结果，表明了桥梁整体刚度良好，自振频率详见表1，振型详见表2。

表1 修正前自振频率实测和理论值汇总表

表2 模型修正前计算与实测振型比较

2.3 基于动力模型修正

（1）修正参数的选择

这里需要注意的是，责任原因排序可以考虑从主要原因和次要原因、直接原因和间接原因、必然原因和偶然原因几个层面进行比较，从而进行依法和依规排序。

在有限元模型修正过程中，结构复杂、参数众多，如何选择参数是一个关键性问题。本文先选取部分影响结构频率的参数（拱肋的弹性模量与密度、横撑的弹性模量与密度、吊杆的弹性模量与密度、横梁的弹性模量与密度、桥面板的弹性模量与密度）作为待修正参数，再对这些选取的参数进行灵敏度分析，依据分析结果选取合适的修正参数。

对待修正参数进行灵敏度分析[6-7]，分析结果表明：拱肋的弹性模量与密度对桥梁结构刚度影响较大，横撑的弹性模量与密度对桥梁结构刚度影响较小，吊杆的弹性模量较密度对结构刚度影响大很多。横梁的弹性模量对桥梁结构的各阶频率有一定的影响，密度则影响较小，桥面板的密度与弹性模量对桥梁的各阶频率都有较大影响，对一阶和三阶的竖弯频率影响比较明显，故本文选取拱肋的弹性模量与密度、横梁的弹性模型、吊杆的弹性模量、桥面板的密度作为修正参数。

本次修正采用联合频率、MAC和模态柔度的目标函数f（x），修正数值模型，有限元模型修正都是基于实测数据为依据，本桥是基于该桥的实测动力特性（模态频率和模态振型）的基础对模型进行修正。

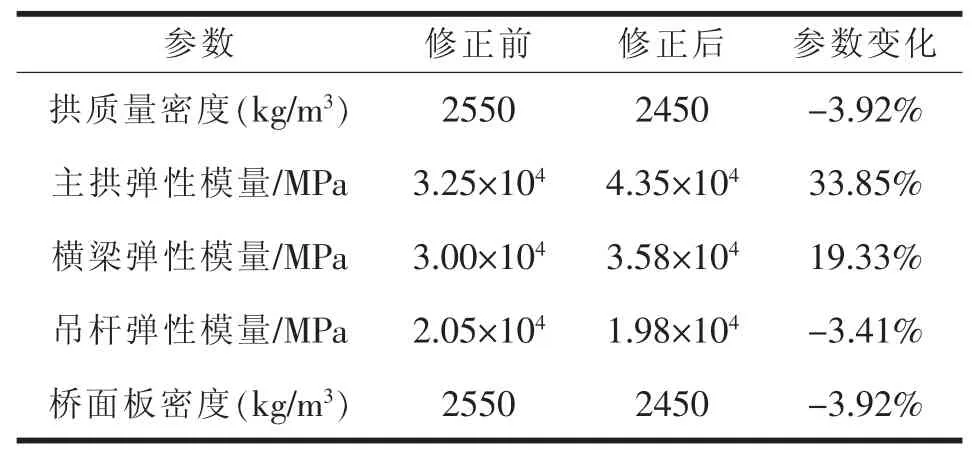
表3 动力参数修正表

（2）动力特性的修正结果

经过修正后的模型的竖向频率与实测频率能够很好地吻合，表明修正后的模型更能符合实际情况，修正后的动力特性和实测的结果详见表4。

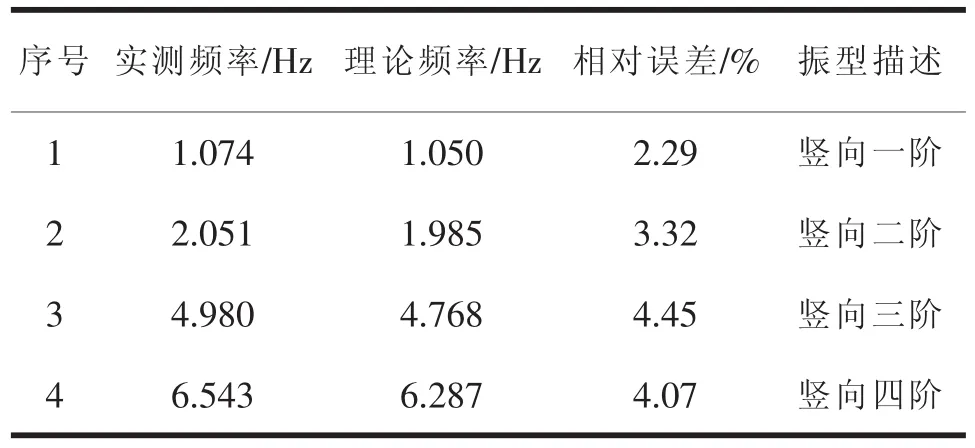
表4 修正后计算和实测动力特性

通过基于动力对混凝土连续梁桥模型的修正表明，采用联合频率、MAC和模态柔度的目标函数进行修正后，模型的动力特性与实测的更为接近。由表4可以看出实测频率、振型与理论值误差值在5%之内，此模型与实际桥梁更为吻合，可用于后面的荷载试验分析，提高桥梁力学分析的精度。

3 静载试验

3.1 试验工况

根据桥梁结构现状，本次静载试验采用汽车加载，在荷载效率η范围内对桥梁加载吨位进行计算，最后确定采用6部36吨后八轮汽车进行静载试验[8-9]。试验荷载效率详见表5。

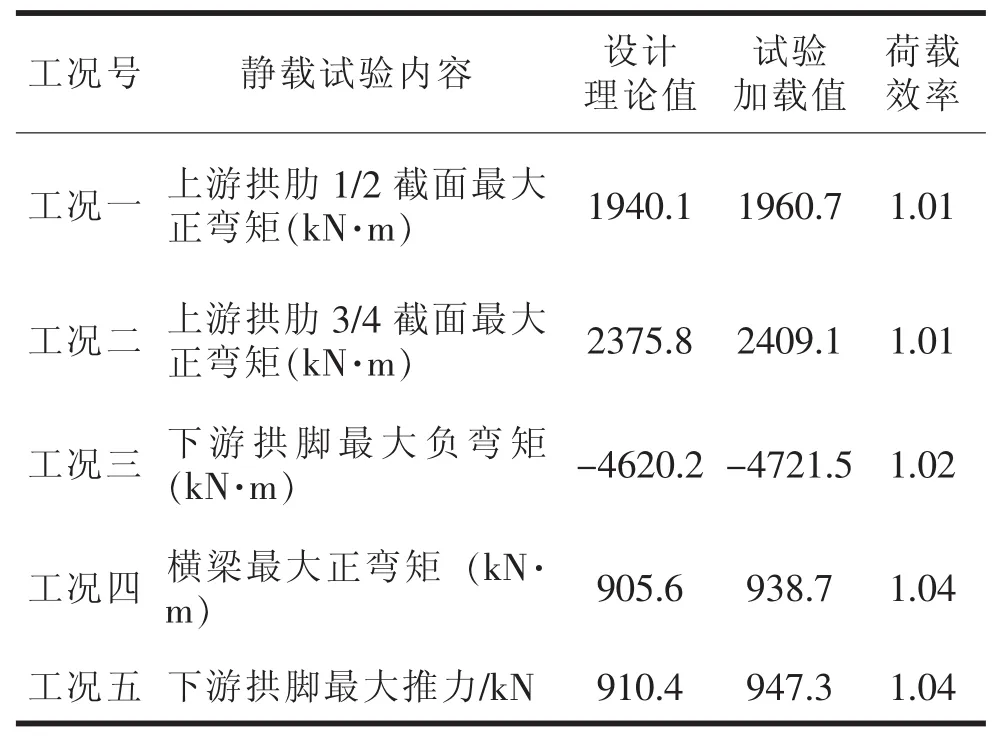
表5 试验荷载效率一览表

3.2 测点布置

（1）测试截面

选择上游拱肋3L/4钢混段截面、3L/4空钢管截面、跨中截面、L/4钢混段截面、下游拱肋国道侧拱脚和7#横梁为测试截面。

（2）应变测点

测点布置于上下游拱肋的1～5和7#横梁底部，测点编号详见图2、图3。

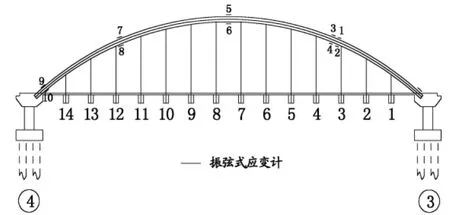
图2 拱肋应变测点编号示意图

图3 7#横梁应变测点编号示意图

（3）挠度测点

挠度测试采用数显收敛仪和精密水准仪同时观测，拱脚位移采用位移计测量。在上游拱肋的1/4截面、1/2截面和3/4截面底部布置收敛仪，在上下游桥面系和第7号横梁桥面处布置水准仪测点，在山前侧下游拱脚桥墩处布置位移计。测点编号详见图4、图5。

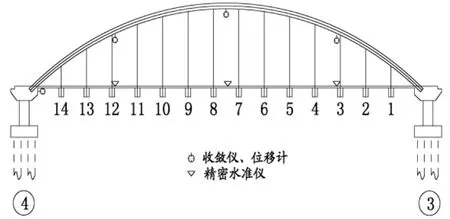
图4 挠度测点布置示意图

图5 7#横梁挠度测点编号示意图

3.3 测试结果

（1）应变测试结果

检测结果表明，所测构件的主要测点应变校验系数在0.80～0.0.89之间，小于规范要求，卸载后应变恢复良好，表明桥梁处于弹性工作状态，强度满足设计要求。

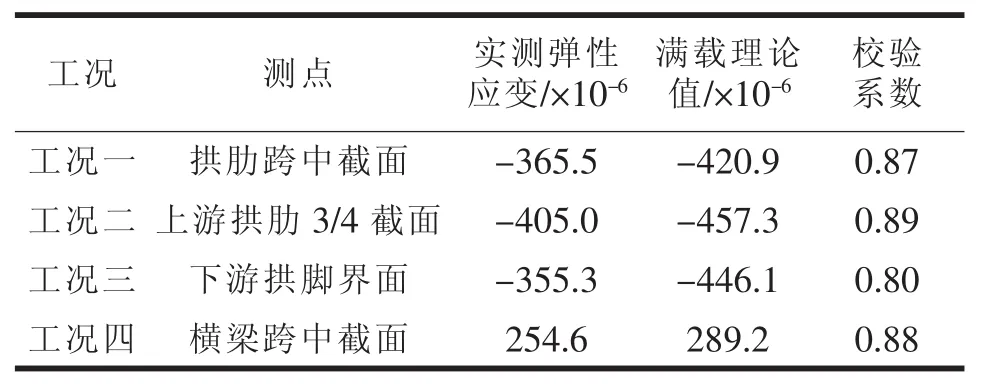
表6 各构件主要测点应变分析

（2）挠度测试结果

检测结果表明，所测构件的挠度校验系数在0.71～0.87之间，小于规范要求，表明桥梁竖向刚度满足设计要求。

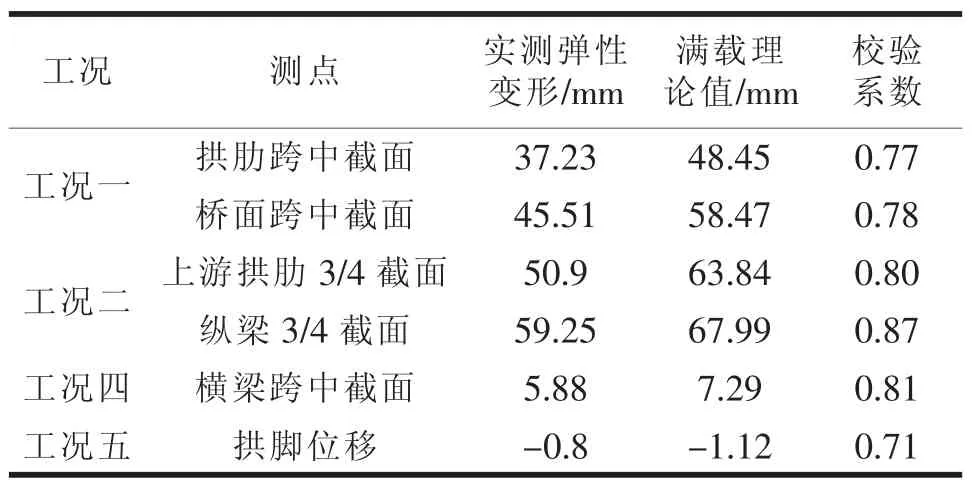
表7 各构件主要测点变形分析结果

本次静载试验荷载效率在1.01～1.04之间，通过修正后的模型，进行静载试验，试验效果良好，模型与桥梁实际状况基本相符合，桥梁各控制截面的强度及刚度均满足设计要求，桥静载试验残余恢复良好，桥梁处于弹性工作状态。

4 结论

（1）通过测定桥梁结构的自振特性及动力响应试验，表明结构的实际动力性能良好；

（2）通过修正参数的灵敏度分析，对以后该类桥梁的修正参数起到参考作用；

（3）基于动力修正后的有限元模型更加符合实际状态，可以用于结构相应状态下的荷载试验分析；

（4）通过静载试验对基于动力修正后的有限元模型进行验证，表明该模型与桥梁实际状况相吻合，可以用于该桥后续的健康运营。

[1]陈宝春.钢管混凝土拱桥设计与施工[M].北京：人民交通出版社，1999.

[2]陈宝春.钢管混凝土拱桥实例集1[M].北京：人民交通出版社，2002.

[3]夏樟华.基于静动力的桥梁结构有限元模型修正[D].福州大学，2006.

[4]李辉，丁桦.结构动力模型修正方法研究进展[J].力学进展，2005.35（2） ：170-180

[5]肖静霆 钢管混凝土拱桥动力特性及动力响应研究[D].哈尔滨：哈尔滨工业大学，2010.

[6]邬晓光，刘英，冯宇，等.基于动态系数的静动力有限元模型修正研究[J].铁道科学与工程学报，2017，14（3）：543-551.

[7]周志红，姜东，陈红亮，等.钢管混凝土拱桥有限元模型修正 [J].南京航空航天大学学报，2010，42（6）：793-796.

[8]JTG/T J21-01-2015，公路桥梁荷载试验规程[S].北京：人民交通出版社，2015.

[9]JTG D60-2015，公路桥涵设计通用规范[S].北京：人民交通出版社，2015.