基于贝叶斯压缩感知的复合材料结构冲击载荷识别研究
严 刚, 孙 浩
(1.南京航空航天大学机械结构力学及控制国家重点实验室, 江苏 南京 210016;2. 麻省理工学院土木与环境工程系, 美国 马萨诸塞州 坎布里奇 MA 02139)
引 言
现代飞行器结构大量使用先进复合材料,但复合材料结构在低能量外物的冲击下,容易造成目不可检的内部损伤,导致结构强度及稳定性的急剧下降,严重威胁飞行安全[1]。因此利用集成在结构中的先进传感元件,准确监测到外物低速冲击并重建冲击载荷时间历程,对及时做出检测和维护决策,提高复合材料结构的安全具有重要意义[2]。
在复合材料结构冲击载荷时间历程识别领域已经发展的技术和方法中,除少数采用神经网络等机器学习方法对大量样本进行训练之外[3],大部分可归类为基于模型的方法。如Chang等基于假设模态法建立了加筋复合材料结构在冲击载荷作用下的动力学模型,通过一种最优平滑滤波算法来重建冲击载荷时间历程[4];严刚等基于Chang等的模型,结合参数化的冲击载荷时间历程,采用微种群遗传算法优化识别了参数,从而近似重建冲击载荷时间历程[5];Hu等通过有限元方法建立了冲击载荷与结构响应之间的关系,采用二次规划最优算法获得冲击载荷时间历程[6]。
在基于模型的冲击载荷时间历程识别中,利用脉冲响应函数在时域进行反卷积的方法被认为是一类数学上直接的方法。但时域反卷积方法的难点在于其不适定性,通常需要进行正则化来获得稳定有界的解[7]。Tikhonov正则化是当前在冲击载荷识别中普遍使用的一种正则化方法[8-11]。在Tikhonov正则化中,一个困难是正则化因子的选取,其选择是否适当直接影响到正则化解的效果[12]。Jin等人在贝叶斯统计推断的理论框架下,提出了一种增广的Tikhnov正则化方法(又称贝叶斯正则化方法),能根据测量数据自适应地确定最优正则化因子[13]。Yan和Sun成功地将之应用于复合材料结构冲击载荷识别,取得了很好的识别效果[14]。
近年来,压缩感知和稀疏正则化方法在信号和图像处理领域取得了很大的成功,因此也被研究者应用于结构冲击载荷识别。如Qiao等采用不同的“字典”来稀疏表示冲击载荷,通过稀疏正则化方法重构这些“字典”的系数来实现对冲击载荷的重建,表明了利用稀疏正则化对冲击载荷识别是可行有效的[15]。但传统的稀疏正则化同Tikhonov正则化类似,也需要事先确定正则化因子。本文针对这一问题,提出一种基于贝叶斯压缩感知的新方法对冲击载荷时间历程进行识别,并通过对复合材料夹层结构进行的实验研究来验证所提出方法的有效性和可应用性。
1 冲击载荷识别模型
在线弹性范围内,结构上任意点的输入-输出关系都可由第一类积分方程表示。假设只有一个冲击载荷f(t)作用于复合材料结构,在结构表面布置了传感器来测量对应的冲击响应ys(t)。若忽略冲击载荷作用点处局部材料退化等因素,可以将复合材料结构视为一时不变系统,冲击载荷与传感点冲击响应之间的关系可表示为如下的卷积

(1)
式中hs(t)为冲击点与传感点之间的脉冲响应函数。
对式(1)在时域进行离散化处理,可获得如下的矩阵形式
Ys=HsF
(2)
其中,
(3)
(4)
(5)
F, Ys,Hs分别为时域离散化后的冲击载荷向量、冲击响应向量和传递函数矩阵,式中f(n),ys(n)和hs(n)分别是f(t),ys(t)和hs(t)在离散时刻tn=nΔt处的值,其中Δt是采样周期,Nsz是采样点数。
式(2)是冲击载荷时间历程识别的基本方程,但由于存在模型误差和测量噪声,式(2)中的传递函数矩阵Hs通常是不适定的,具有很大的条件数。因此对式(2)直接求逆来识别冲击载荷,通常得到的解是不稳定的,具有非常大的误差,需要引入正则化来获得近似的稳定有界解。
2 稀疏正则化系数重构问题
为识别冲击载荷时间历程,本文首先提出采用一组共M个高斯核函数作为基函数来表示未知冲击载荷。高斯核函数的形式为
(6)
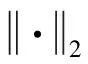
F=GQ
(7)
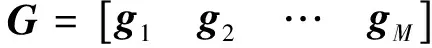
将式(7)代入式(2),则冲击响应向量与基函数系数向量之间的关系可以表示为
Ys=TQ
(8)
其中
Τ=HsG
(9)
对于冲击载荷,采用高斯核函数表示后,基函数系数向量具有高度稀疏性,因此冲击载荷时间历程识别问题可转换为下式描述的基于L2-L1范数的基函数系数稀疏正则化重构问题
(10)
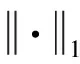
3 贝叶斯压缩感知
本文采用贝叶斯压缩感知来对式(10)描述的稀疏正则化问题进行求解,其优点是可以避免式(10)中正则化因子的选取[16]。采用贝叶斯建模方法,将系数向量Q封装在后验概率密度函数p(Q|Ys,α,σ2)中,由贝叶斯定理可得[17]
(11)
式中p(Ys|Q,σ2)是似然函数,p(Q|α)是未知系数向量的先验概率密度函数,p(Ys|α,σ2)是边缘似然函数。
假设测量获得的冲击响应与模型输出之间的误差满足均值为零、方差为σ2的高斯分布(σ2未知),似然函数可写为
(12)
同样定义Q的先验分布为高斯分布,写为
(13)

将式(12)和(13)代入式(11),可以得到
(14)
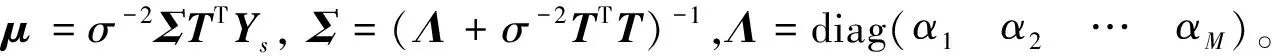
为确定超参数向量α和误差方差σ2,采用相关向量机方法进行求解。这归结为一个第二类型的最大似然问题,其形式为[18]
(15)
其中,Ω=σ2I+TΛ-1TT。式(15)的详细算法可参阅文献[18]。
将获得的超参数向量α和误差方差σ2代入解向量Q的后验概率密度函数p(Q|Ys,α,σ2),并以p(Q|Ys,α,σ2)最大处对应的值作为未知系数向量Q的最大后验概率解,代入式(7)就可实现冲击载荷时间历程的识别。
4 实验研究
4.1 实验装置与试验件
为验证本文所提出方法的有效性和可应用性,建立了如图1所示的实验系统,在一复合材料夹层结构上进行实验研究。该夹层结构呈六边形,主要尺寸如图2所示,上下表面面板采用T300/3234碳纤维预浸料层合而成,上面板厚度为5 mm,下面板厚度3 mm,夹芯层采用PMI泡沫,厚度为17 mm。在上面板表面粘贴了4个直径为10 mm,厚度为1 mm的PZT压电片,分别命名为S1, S2, S3, S4,组成传感网络,用于监测冲击载荷作用下结构的动态应变。建立了如图2所示的直角坐标系,各个PZT压电片的坐标在表1中列出。实验中考虑了6个随机选定的冲击点,分别命名为IP1, IP2, IP3,IP4, IP5, IP6,其坐标在表2中列出。实验时将复合材料夹层结构固定在支架上,采用PCB 086C03力锤在结构上施加冲击载荷,冲击载荷信号通过B&W 61001功率放大器供电放大后被NI PXIe-5105数字化仪采集,结构在冲击载荷作用下的响应由PZT压电片感应后同样由数字化仪采集,采样频率设置为50 kHz。

图1 实验装置与试验件Fig.1 Experimental setup and test structure
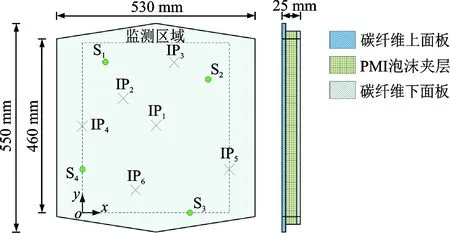
图2 复合材料夹层结构示意图Fig.2 Illustration of sandwich composite structure

S1S2S3S4坐标/mm(50, 350)(350, 300)(300, 0)(0, 100)

表2 冲击点位置信息
实验分为两个阶段,第一阶段采用模态实验方法获得各冲击点与各传感器之间的脉冲响应函数。首先应用力锤在各冲击点连续冲击3次,同时记录PZT压电片测量到的动态响应信号,经傅里叶变换,获得冲击点与各传感器之间的平均频响函数,然后再由逆傅里叶变换获得传递函数矩阵。第二阶段,再次对各冲击点进行冲击,记录PZT压电片获得的冲击响应,用于对冲击载荷时间历程进行识别。图3所示为力锤作用在IP1时的冲击载荷时间历程及对应的冲击响应信号,其余位置的冲击载荷时间历程与冲击响应信号与此类似。
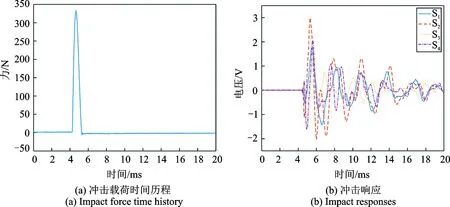
图3 力锤作用在冲击点IP1时信号Fig.3 Measured signals when impact hammer acts on impact point IP1
4.2 实验结果
为了对冲击载荷时间历程进行识别,需要确定作为基函数的高斯核函数。本文中高斯核函数的个数设为M= 501,每个核函数宽度设置为均匀相等,取hk=T/(M-1),其中T为冲击响应信号的时间长度,本文中取T= 20 ms。每个核函数的中心位置均匀地分布在整个时间域上,即tk=(k-1)hk(k= 1,2,…,M)。图4所示为第101个高斯核函数的示意图。
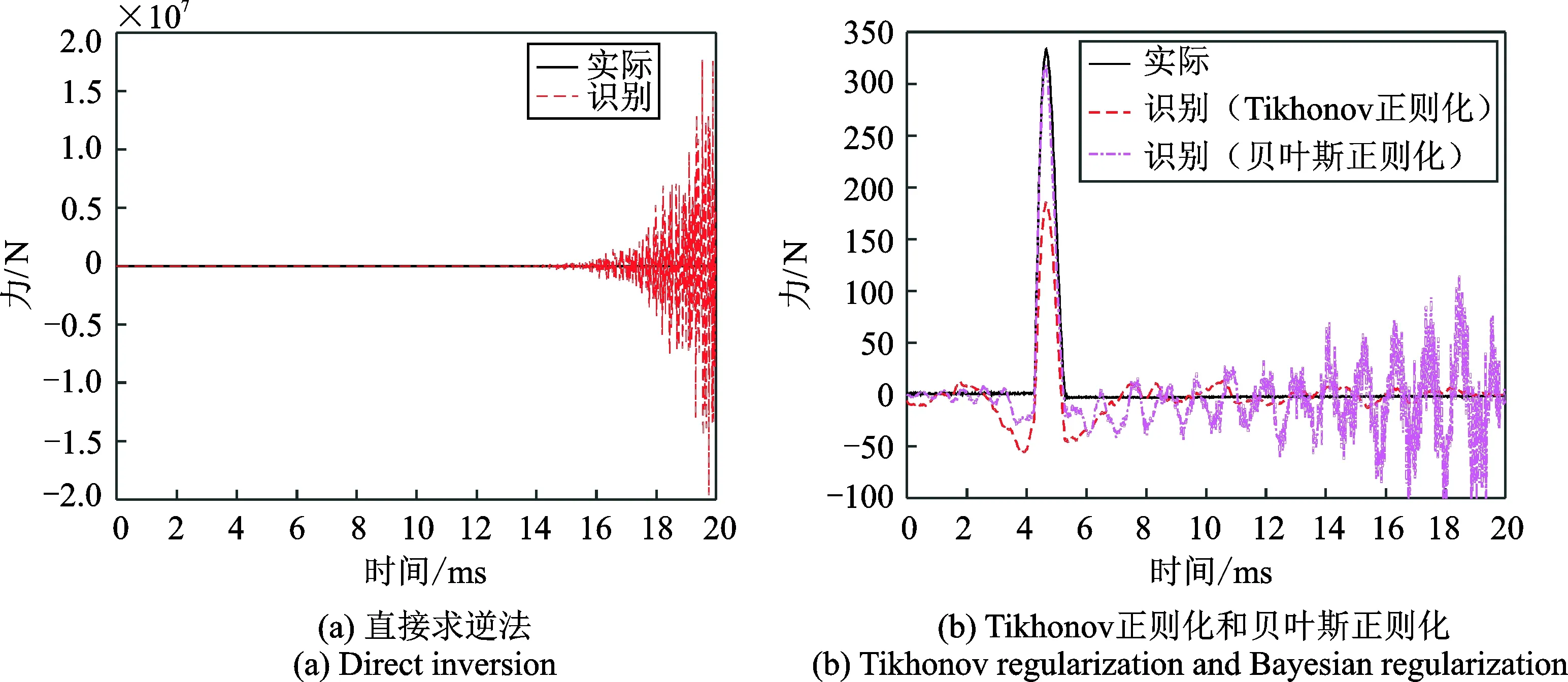
图5 传感器S1响应识别冲击点IP1处冲击载荷结果Fig.5 Identification results for impact point IP1 by S1 response
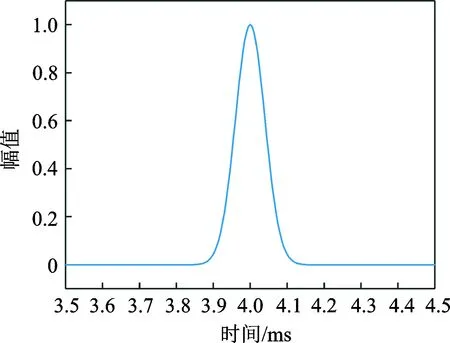
图4 基函数中第101个高斯核函数示意图Fig.4 101st Gaussian kernal function
接着对所采集到的各组冲击响应信号进行分析来识别对应的冲击载荷时间历程。为了比较识别效果,分别采用直接求逆法、Tikhonov正则化和贝叶斯正则化3种方法进行对比。图5(a)所示为冲击载荷作用在冲击点IP1时,采用传感器S1的响应信号直接求逆识别的结果。从图中可以看出,由于传递函数矩阵的不适定性,直接求逆的解是不稳定的,超出实际冲击载荷几个数量级。图5(b)所示为采用Tikhonov正则化和贝叶斯正则化对同一响应信号进行识别的结果,其中Tikhonov正则化因子由L曲线法确定[12]。由图中可以看出,L曲线选择的正则化参数虽然消除了解的不稳定性,但识别的冲击载荷低于实际的冲击载荷,表现为明显的过正则化;而贝叶斯正则化从测量数据中自适应地确定了正则化因子,在一定程度上识别出了冲击载荷的主要部分,但其识别结果尾部具有很强的振荡性,且和Tikhonov正则化识别结果一样存在负分量,仍需进一步改进。

图6 本文方法识别IP1处冲击载荷结果(采用的响应来自S1, S2, S3, S4)Fig.6 Identification results for impact point IP1 with the proposed method(by responses from S1, S2, S3, S4)
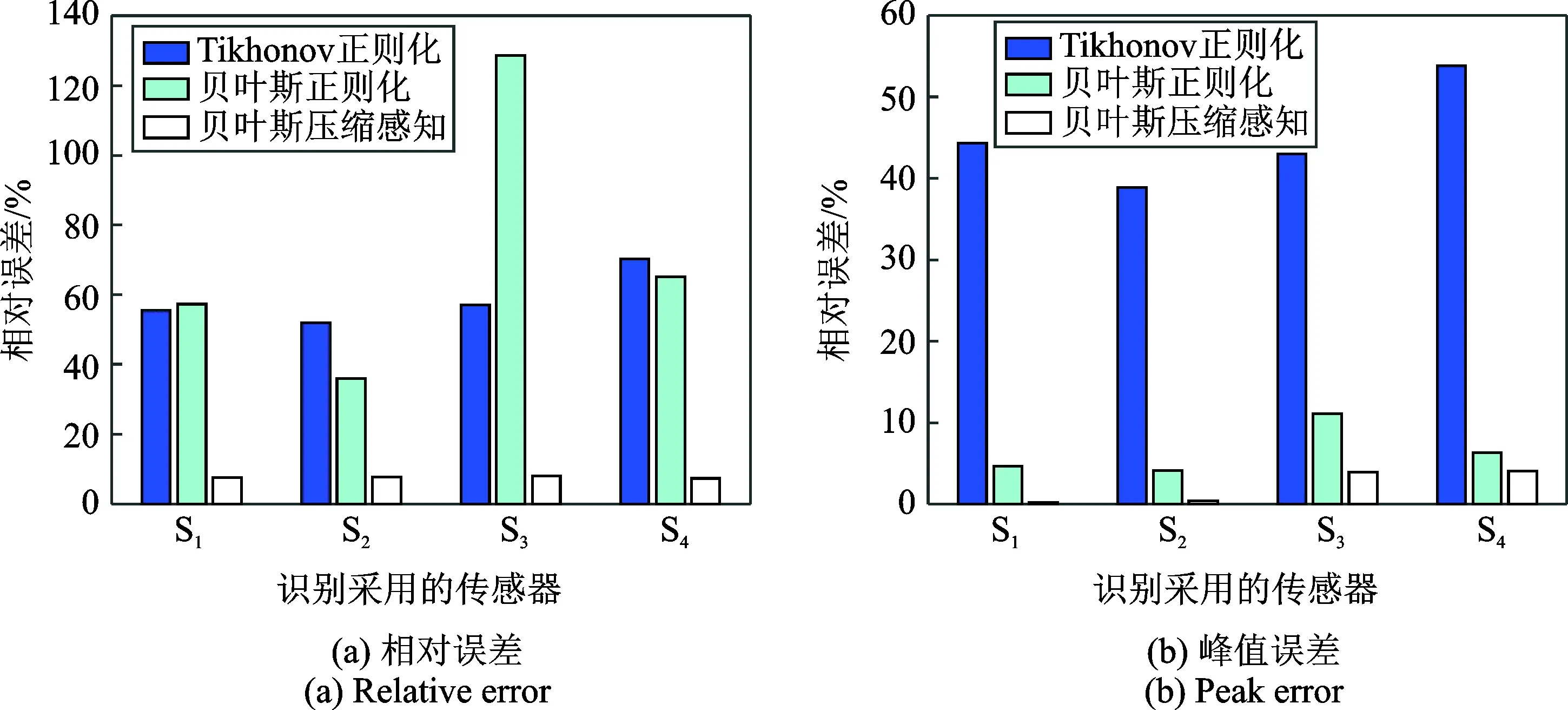
图7 采用不同传感器响应识别冲击点IP1处冲击载荷误差Fig.7 Error of the identification results for impact point IP1 by different sensor responses
图6(a)所示为冲击载荷作用在冲击点IP1时,采用本文所提出方法对传感器S1的响应信号进行识别的结果。从图上可以看出,识别的冲击载荷时间历程比较平滑,没有明显的振荡,与实际的冲击载荷吻合得非常好,识别的冲击载荷的形状、时间长度以及峰值基本与实际的一致。图6(b)~(d)所示分别为冲击载荷作用在冲击点IP1时,本文所提出方法对其他3个传感器信号进行识别的结果,从图中可以看出,都取得了很好的识别效果。
同样,对其他冲击点的冲击载荷进行识别时,本文所提出方法也都能获得类似的识别结果,与实际冲击载荷很好地吻合。为了进一步比较识别结果的准确性,定义相对误差为
(16)
以及峰值误差为
(17)
式中Ftrue和Freconstructed分别表示实际和识别的冲击载荷时间历程。图7(a)和(b)所示是不同方法分别利用4个传感器响应信号识别冲击点IP1处冲击载荷的相对误差和峰值误差比较。
图8(a)和(b)所示是不同识别方法对不同冲击点处冲击载荷识别的平均相对误差和平均峰值误差比较(4个传感器响应识别误差的平均值)。从图8中可以看出,与Tikhonov正则化以及贝叶斯正则化方法相比,本文所提出方法显著降低了识别结果的误差,在本文实验研究的6个冲击点冲击载荷识别结果中,最大相对误差仅为12.25%,最大峰值误差仅为7.23%,表明本文所提出方法识别的冲击载荷与实际冲击载荷基本一致,验证了其有效性和可应用型。
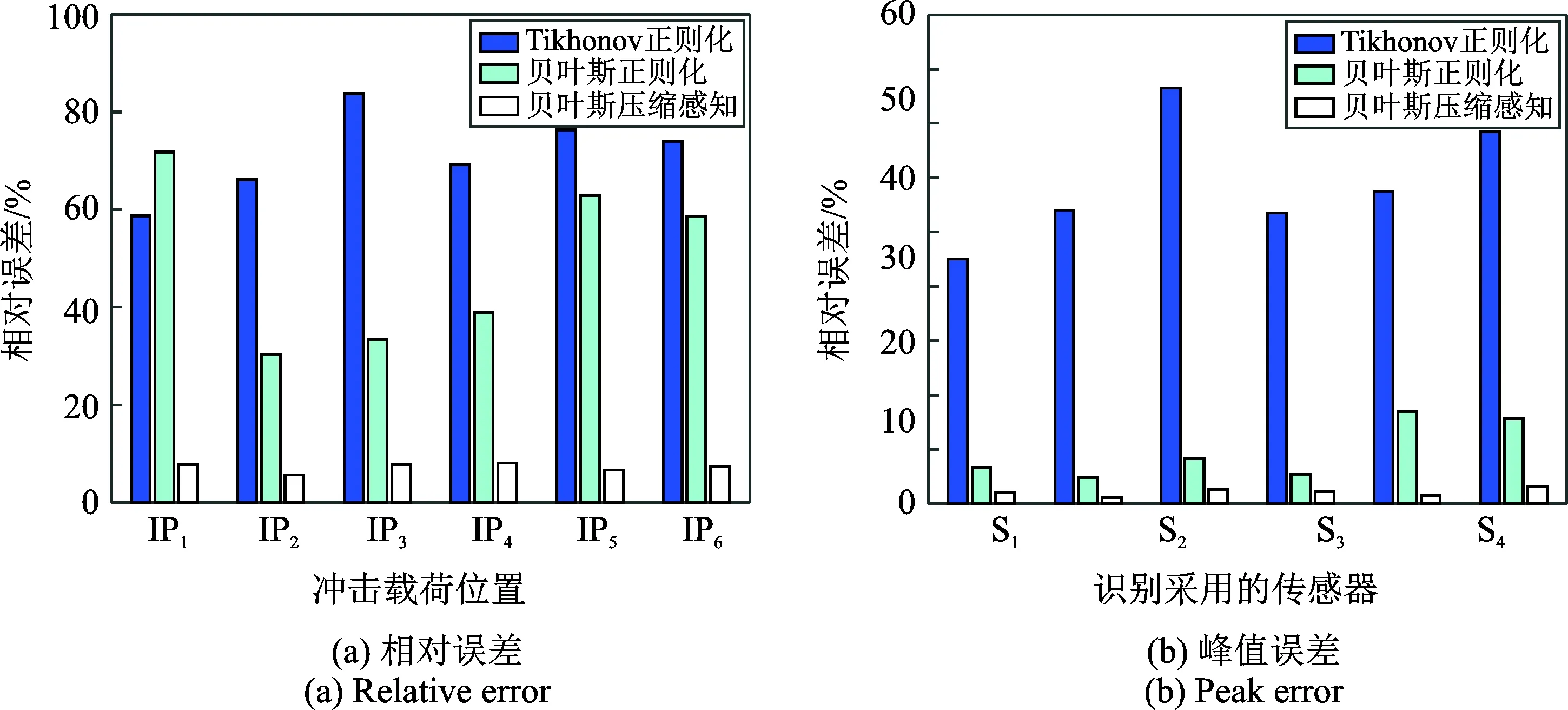
图8 不同冲击点处识别冲击载荷的平均误差Fig.8 Average error of the identification results for different impact points
5 结 论
本文提出了一种基于贝叶斯压缩感知的新方法,对作用在复合材料结构上的冲击载荷时间历程进行识别。在采用一组高斯核函数近似表示未知冲击载荷时间历程后,将冲击载荷重建问题转换为基函数系数的稀疏正则化重构问题,通过贝叶斯压缩感知方法来求解该稀疏正则化重构问题,获得基函数的最优稀疏系数,继而重建冲击载荷时间历程。
对复合材料夹层结构的实验研究结果表明:本文提出的方法能准确地识别冲击载荷时间历程,识别的冲击载荷与实际的冲击载荷吻合非常好,其形状、时间长度及峰值与实际冲击载荷基本一致,定义的相对误差小于15%,峰值误差小于10%,均显著低于Tikhonov正则化和贝叶斯正则化的识别误差,表明了本文所提出方法的有效性和可应用性。
致谢 感谢南京航空航天大学航空宇航学院王新峰副教授提供的复合材料夹层结构用于本文的实验研究。
[1] 沈 真, 杨胜春, 陈普会.复合材料抗冲击性能和结构压缩设计许用值 [J]. 航空学报, 2007, 28(3): 561-566.
Shen Zhen, Yang Shengchun, Chen Puhui. Behaviors of composite materials to withstand impact and structural compressive design allowableness [J].ActaAeronautica Et Astronautica Sinica, 2007, 28(3): 561—566.
[2] Staszewski W J, Mahzan S, Traynor R. Health monitoring of aerospace composite structures - active and passive approach [J]. Composites Science and Technology, 2009, 69(11-12): 1678—1685.
[3] Ghajari M, Sharif-Khodaei Z, Aliabadi M H, et al. Identification of impact force for smart composite stiffened panels [J]. Smart Materials and Structures, 2013, 22(8): 085014.
[4] Seydel R, Chang F K. Impact identification of stiffened composite panels: I. system development [J]. Smart Materials and Structure, 2001,10(1): 354—369.
[5] 严 刚, 周 丽.加筋复合材料结构的冲击载荷识别 [J]. 航空学报, 2008, 29(5): 1150—1156.
Yan Gang, Zhou Li. Impact load identification for stiffened composite structure [J]. Acta Aeronautica Et Astronautica Sinica, 2008, 29(5): 1150—1156.
[6] Hu N, Fukunaga H, Matsumoto S, et al. An efficient approach for identifying impact force using embedded piezoelectric sensors [J]. International Journal of Impact Engineering, 2007, 34(7): 1258—1271.
[7] Inoue H, Harrigan J J, Reid S R. Review of inverse analysis for indirect measurement of impact force [J]. Applied Mechanics Review, 2001, 54(6): 503—524.
[8] Jacquelin E, Bennani A, Hamelin P. Force reconstruction: analysis and regularization of a deconvolution problem [J]. Journal of Sound and Vibration, 2003, 265(1): 81—107.
[9] 王 锋, 武 龙, 张小庆, 等.动态载荷辨识问题的正则化求解新方法 [J].振动工程学报, 2016, 29(1): 31—37.
Wang Feng, Wu Long, Zhang Xiaoqing, et al. A technique for solving dynamical force identification problems by Tikhonov regularization method [J]. Journal of Vibration Engineering, 2016, 29(1): 31—37.
[10] 马 超, 华宏星.一种基于新的正则化技术的冲击载荷识别法 [J].振动与冲击, 2015, 34(12): 164—168.
Ma Chao, Hua Hongxing. Impact force identification based on improved regularization technique [J]. Journal of Vibration and Shock, 34(12): 164—168.
[11] 常晓通, 闫云聚, 刘 鎏, 等.基于Green函数和正则化的动态载荷识别方法 [J].振动、测试与诊断, 2014, 34(1): 124—129.
Chang Xiaotong, Yan Yunju, Liu Liu, et al. Applications of regularization method in dynamic load identification [J]. Journal of Vibration, Measurement & Diagnosis, 2014, 34(1): 124—129.
[12] Hansen P C. Analysis of discrete ill-posed problems by means of the L-curve [J]. SIAM review, 1992, 34(4): 561—580.
[13] Jin B, Zou J. A Bayesian inference approach to the ill-posed Cauchy problem of steady-state heat conduction [J]. International Journal of Numerical Methods in Engineering, 2008, 76(4): 521—544.
[14] Yan G, Sun H, Büyüköztürk O.Impact load identification for composite structures using Bayesian regularization and unscented Kalman filter [J]. Structural Control and Health Monitoring, 2017, 24(5): e1910.
[15] Qiao B J, Zhang X W, Wang C X, et al. Sparse regularization for force identification using dictionaries [J]. Journal of Sound and Vibration, 2016, 368: 71—86.
[16] Ji S, Xue Y, Carin L. Bayesian compressive sensing [J]. IEEE Transactions on Signal Processing, 2008, 56(6): 2346—2356.
[17] 茆诗松, 汤银才.贝叶斯统计 [M].北京: 中国统计出版社, 2012.
Mao Shisong, Tang Yincai. Bayesian Statistics [M]. Beijing: China Statistics Press, 2012.
[18] Tipping M E. Sparse Bayesian learning and the relevance vector machine [J]. Journal of Machine Learning Research, 2001, 1: 211—244.

