应急救援车辆装备器材快速布局设计方法
, ,,
(1.徐州工程机械集团有限公司,江苏 徐州 221004; 2.徐工集团江苏徐州工程机械研究院,江苏 徐州 221004;3.高端工程机械智能制造国家重点实验室,江苏 徐州 221004)
随着我国应急救援装备的迅速发展,救援装备的种类和数量有了很大提升.应急救援器材车作为关键车辆装备之一,其关键点为器材布局的科学性和合理性而设计,既要最大限度提高车辆的空间利用率,又要保证救援人员在存取和使用器材时可以更加快捷、方便、安全.目前救援车辆的器材布局设计主要依据使用对象的调研需求和设计人员的布局经验,这种定性的设计方法主观性较强,缺乏科学性,布局方案的合理性也缺乏统一的评价标准.同时,救援车辆器材箱的设计还以定制为主,设计周期长,效率低.
关于应急救援车辆装备器材的布局研究,国内专家的关注度也越来越高.姚澜等[1]提出利用相关表法构建器材的重要性和器材间关联度的关系矩阵排列出主次关系,将使用频率和关联度高的器材结合人体存取的方便性进行布局设计.刘小霞等[2]提出利用JACK仿真软件对消防车器材布局进行了人机工程学方面的视域和可达域分析,在此基础上结合人体尺度原则、器材布局原则进行了布局优化和评价.沈健等[3]提出基于人因工程的器材布局优化设计方法,利用人与设备间的使用关系矩阵,以及加权计算人因需求关系举证与非人因需求关系矩阵后得到的综合需求关系矩阵,对设备进行布局设计,并运用JACK仿真软件进行了视域分析和可达域分析验证其可行性.总体来说,以往的研究重点在于建立人与器材或器材与器材之间的关系理论用于指导布局,并结合JACK仿真软件或其他人机工程学分析方法对布局进行优化分析或评价,对于布局实施的具体方法存在缺失.
因此,本文将器材布局归属于布局问题中的三维空间装填问题,提出一种基于启发式算法的器材装备快速布局设计及优化方法.结合器材布局原则及人体尺寸原则建立器材布局设计及优化模型,设计布局规则及其相应的启发式算法,快速制定器材的布局方案.
1 布局设计框架分析
器材布局归属于布局问题中的三维空间装填问题,即在器材箱体内按一定的规则摆放形状、大小不同的器材.这类布局问题约束和目标较多,求解较为困难.针对此类问题,求解的方法主要有图论法、演化算法、归纳法、遗传算法、粒子群算法、启发式算法[4-7]等.
1.1 布局问题描述及定义
器材箱体为给定的布局空间,器材为待布器材包括个人防护类、救生类、破拆类等8大类.由于待布器材结构上存在较大差异,布局设计需要将其按性能约束固定存放于器材箱体内,布置完成后需满足下述目标:① 各待布器材间不得有干涉并保持给定距离;② 待布器材不得超出给定的布局空间;③ 布局后整个系统的质心应在一定范围内;④ 布局空间尽可能小,即空间利用率最大化;⑤ 符合使用频率、重要性等原则,便于存取.
1.2 布局思想及设计流程
运用现代设计方法提出一种串联布局理论与布局优化的计算方法.当待布器材和布局空间确定以后,待布器材与布局空间以及待布器材间的关系均可以确定.首先,分析待布器材与人及待布器材间的关联度,得出待布器材的布置顺序;然后,建立数学模型;最后,根据布置原则制定规则后设计启发式算法进行迭代计算,得出布局方案.
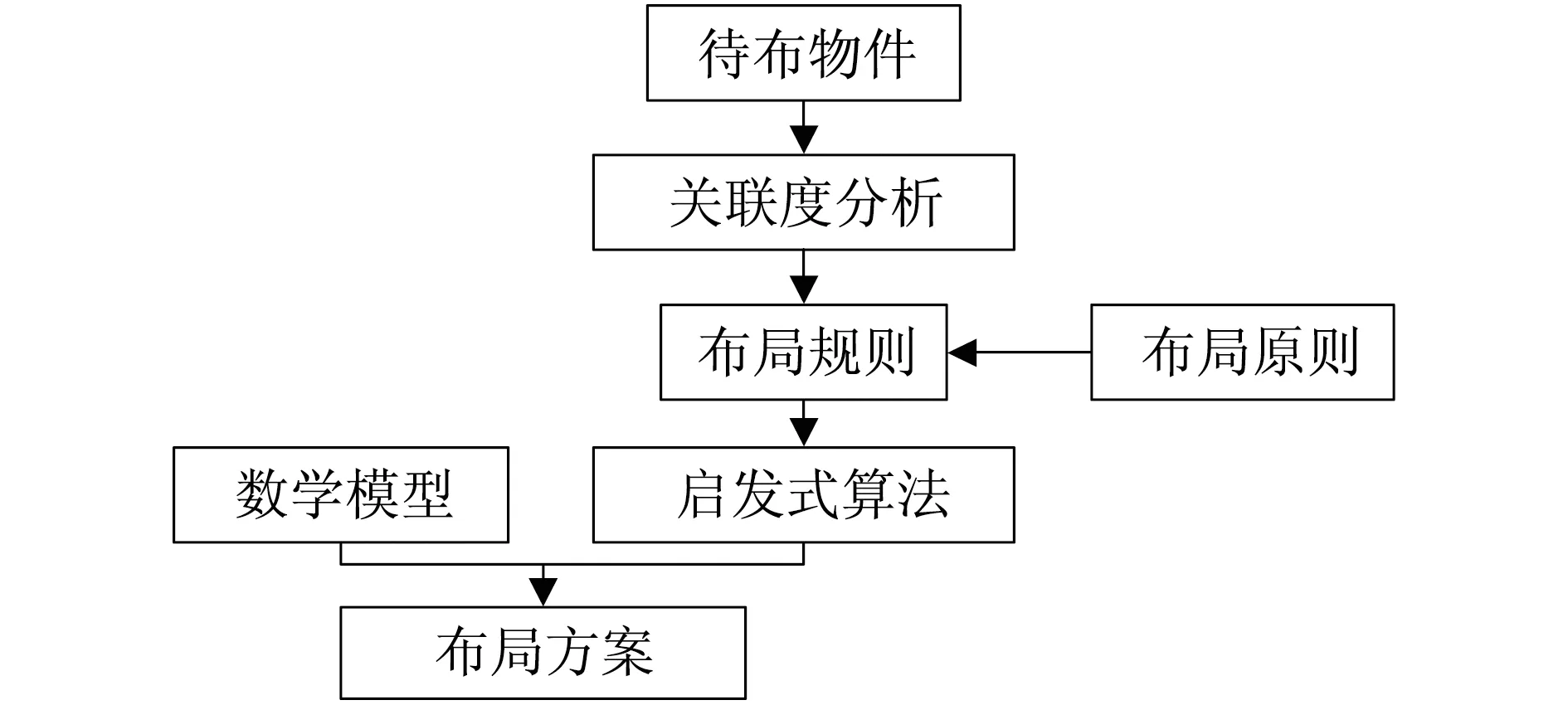
图1 布局设计思想Fig.1 Framework of the proposed layout model
整个布局过程可分为以下几个步骤:① 建立待布空间和待布器材的几何信息.待布器材的几何信息包括长×宽×高(长方形)或直径×长度(圆柱形)、质量,待布空间为边界尺寸.② 器材分类.按8大类器材进行划分类别,形成8个待布器材集,实现器材的模块化布局.③ 关联度分析.分别建立8个待布器材集的关系矩阵,分析件与件之间的关系度,便于集中布局.遵循使用频率和重要度布局原则,分析件与人之间的关系度,形成关系矩阵和内外层的空间规划.④ 建立数学模型.布局的目标为空间利用率最大化.根据布局目标建立布局优化目标函数,其他的目标作为约束条件,例如待布器材间不干涉、待布器材间距、整个系统限制于规定范围内等.⑤ 设计启发式算法.首先制定待布器材的提取规则和摆放规则,然后根据空间规划进行内外层布局,同时校核系统质心位置,最后进行空间利用率迭代计算.⑥ 形成方案.计算结果输出为各待布器材的位姿数据,从而形成布局方案.
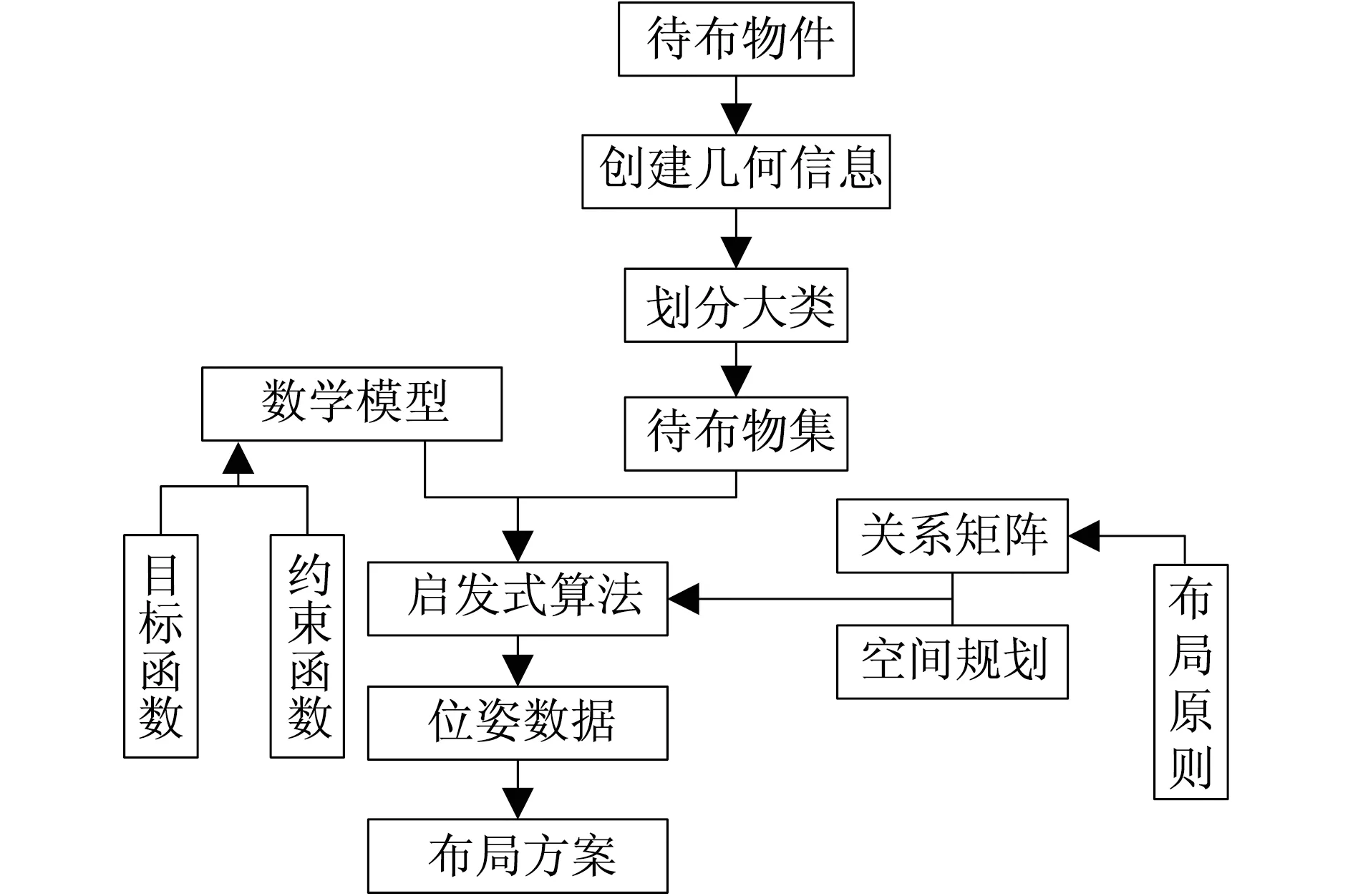
图2 布局设计流程图Fig.2 Flowchart of the proposed layout model areas
2 设计及优化过程
2.1 建立待布器材信息并分类
救援器材的形状各异,布局时采用单元格分割的方式,且器材之间保持规定的距离,故将器材的形状简化,全部统形为长方形,其几何参数包括长×宽×高(长方形)、质量、件数,并进行分类编号,按8大类器材分别建立信息几何,共8个待布器材集N={N1,N2,…,N8},集合信息如表1所示.

表1 救援器材几何数据表Tab.1 Rescue equipment geometric data set
2.2 关联度分析
救援器材的布局主要考虑救援人员的操作性和安全性等因素,需遵循器材的布置原则指功能原则、使用频率原则、重要性原则、使用顺序原则等,其内容实质性反映的是“器材”与“器材”之间以及“器材”与“人”之间关系.功能性原则为功能相似的器材统一布置,即为8个待布器材集.使用频率原则为人最容易、最舒适取用的区域放置使用频率较高的器材,即为“人”与“器材”的关系度.重要性原则为救援任务实施的关键性器材,表现也为“人”与“器材”的关系度.使用顺序原则为一些器材组合使用或先后使用,即为“器材”与“器材”的关系度.下面将布置原则通过关系矩阵进行分析表示.
使用频率原则关联度用关系矩阵A表示,采用r表示人与器材间的关系度,使用频率较高的关系度定义为r=1,使用频率较低的关系度定义为r=0,根据多次消防部队的实地调研结果,建立关系矩阵A,如表2所示.
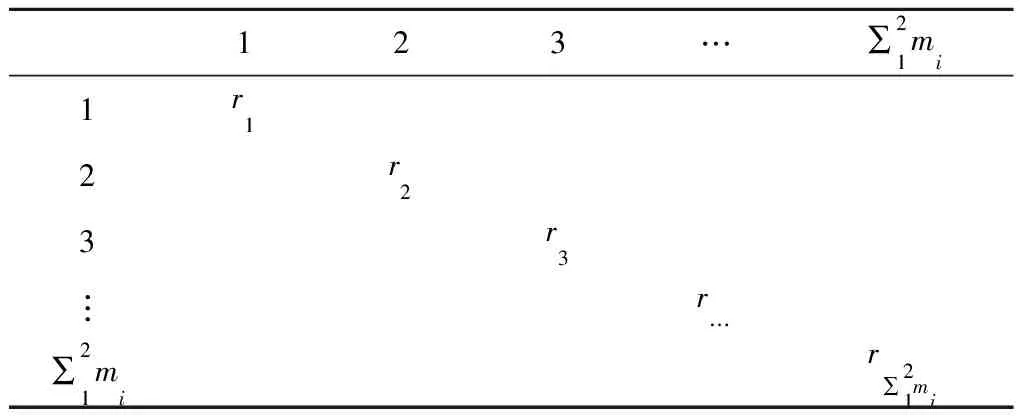
表2 矩阵关系ATab.2 Correlation matrix A
重要度原则关联度用关系矩阵B表示,采用s表示人与器材间的关系度,比较重要的器材关系度定义为s=1,重要度较低的关系度定义为s=0,根据多次消防部队的实地调研结果,建立关系矩阵B,如表3所示.
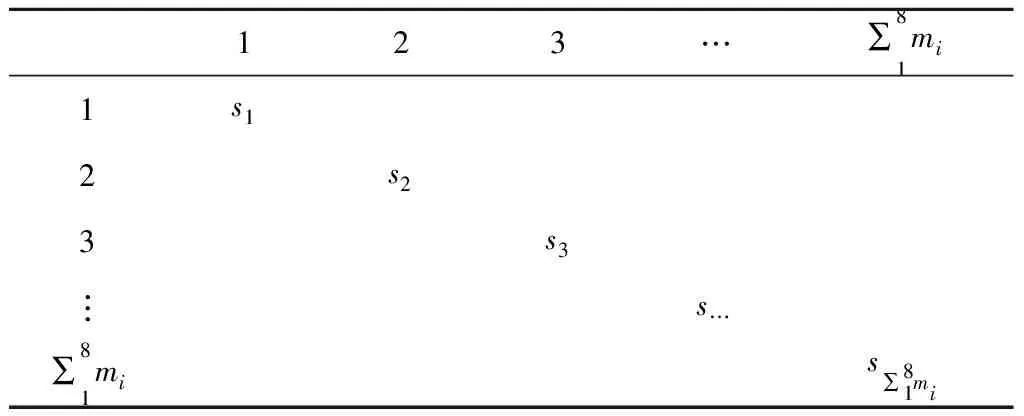
表3 矩阵关系BTab.3 Correlation matrix B
关系矩阵A和关系矩阵B皆反映了人与器材件的关系度,故可将表2和表3进行合并求得综合关系矩阵C,关系度用g=r+s来表示.g≥1的表示器材与人的关系度比较密切,从而将其布置在箱体最外层,方便操作人员的存取;g<1的表示器材与人的关系度较小,故将其布置箱体内层,在此基础上实现器材的总体空间划分[8],用于设计器材的布置规则.
使用顺序原则关联度用关系矩阵D表示,采用t表示器材与器材间的关系度,器材之间需要配合使用的关系度定义为t=1,器材独立使用的关系度定义为t=0,根据多次消防部队的实地调研结果和器材的使用特性,建立关系矩阵D,如表4所示.

表4 矩阵关系DTab.4 Correlation matrix D
关系矩阵D1中:t=1时,表示这两种器材需就近布置,便于操作者使用:t=0时,表示这两种器材无关系,布局时无需考虑其间关系.
2.3 建立数学模型
器材布局主要的设计目标是空间利用率最大化和人机性最优化,其中空间利用率可定量表示和分析,人机性只能定性分析.通过关联度分析,将人机化的要求转化为关系矩阵,嵌入算法中,所以将设计及优化的目标定为空间利用率最大化,即为器材布局所占的空间体积与箱体体积的比值最大.其他目标转为约束条件:整个器材布局的质心在容许范围内;器材不超过箱体边界;相邻器材无干涉等.
待布器材集合
N={N1,N2,…,N8}=
{nij|nij∈Ni,i=1,2,…,8;j=1,2,…,mi}
通过以上分析,该器材布局的目标函数为
式中:vij为器材nij的体积;Vc为器材箱体的有效容积.
便于描述后续空间位置尺寸,建立直角坐标系:以车辆前进方向为基准,箱体右下前角为坐标原点,箱体下表面为xy平面,x轴为箱体前下边缘,正方向由右向左;y轴为箱体右下边缘,正方向由前向后;z轴垂直于箱体底面向上.
要求器材布局的质心在容许范围内可描述为
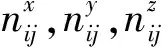
要求器材布局不超过箱体边界可描述为
aij≤W
bij≤L
hij≤H
式中:aij,bij,hij分别为器材nij布局后的x,y,z3个方向的坐标长度值;L,W,H分别为箱体有效的长、宽、高.
2.4 设计算法
器材布局需解决的问题是空间利用率最大化、平衡布局(保证重心位置)以及人性化要求.按照将器材布局原则转化的综合关系矩阵,提出待布器材的提取、布置方式与待布空间相匹配的构造方法;利用空间规划的思路,提出先外层后内层的布局策略,将问题转化为带已布物群约束的布局.基于以上方法,设计适用于器材布局的启发式算法.
2.4.1待布器材的提取规则
根据关系矩阵C的分析,使用频率高和重要的器材布置在外层,便于存取.
算法1首先,提取外层待布器材集N外={N1外,N2外,…,N8外},Ni外即g≥1和t=1器材组成的合集;然后提取内层待布器材集N内={N1内,N2内,…,N8内},Ni内即g<1和t=0器材组成的合集;最后,需对Ni外和Ni内分别进行排序,Ni外排序的方式是先将g≥1的器材按质量进行降序排列,将t=1的器材按相关性穿插进行序列二次调整,并将有相关度的器材进行绑定,Ni内排序的方式是先将g<1的器材按质量进行降序排列即可.
2.4.2设计算法
布局采用先外层后内层,布局方式为顺序摆放策略,分别从右下角和左下角开始,将器材沿着箱体两外侧面进行堆垛,然后再进行内层的摆放布局.
算法2外层布置规则:提取Ni外集合中的奇数项形成子集Pi1,提取Ni外集合中的偶数项形成子集Pi2,分别计算子集合的最小面积minS.左侧外层依序提取Pi1集合中的器材按最小面积组合进行堆垛,右侧外层依序提取P2集合中的器材按最小面积组合进行堆垛,左右两侧交替进行,过程中进行干涉检查.若干涉需进行摆放面调整,
外层布置完成后,内层布置问题已转化为带已布物群约束的布局问题,内层的布局需在外层器材布局后形成的待布空间内进行布局.
定义1凹凸度[9].以外层布局面的最低点为基点,规定经过基点的横截面为外层布局面的底面,则由外层布局面底面之上的器材的顶点坐标确定为外层布局面的凹凸度.凹凸度将决定放入器材的外形.
定义2待布空间T.在器材布局方式一定的前提下,每布置一件器材都对应形成一个待布空间.
定义3待布空间的匹配集R.待布器材集中与待布空间的高度或长度尺寸相接近的器材称为待布空间的匹配集.
引入小块预留策略[9],对凹凸的外层空间进行分隔计算,优先布局体积小的器材,减小零碎空间,从而提高车辆空间的利用率.
内层的布置方式为在xz平面上逐层进行码放,分为两种码放顺序:xy→z和yx→z.
算法3内层布置规则:① 凹凸度计算.计算内层待布空间T的凹凸度,寻找Ni内的一个子集R,分别满足不同的凹凸度,减小零碎空间.② 先以xy→z布置方式进行剩余器材集合的逐层布置,计算待布空间T的长或宽,寻找剩余Ni内的一个子集R′,使R′中的元素长度之和≈T的长,高度相当,质量相近.然后将R′按元素宽度进行递减次序排列后,逐次堆放于待布空间内.③ 并核算空间利用率和约束条件,形成布局方案1.④ 以xy→z布置,重复步骤2和3,形成布局方案2,比较空间利用率是否有改善后,输出布局方案1或方案2.
2.5 布局方案数据
初始条件为待布器材集和箱体的空间,运用2.3节的启发式算法,可得出器材布局的布置信息,如表5所示.
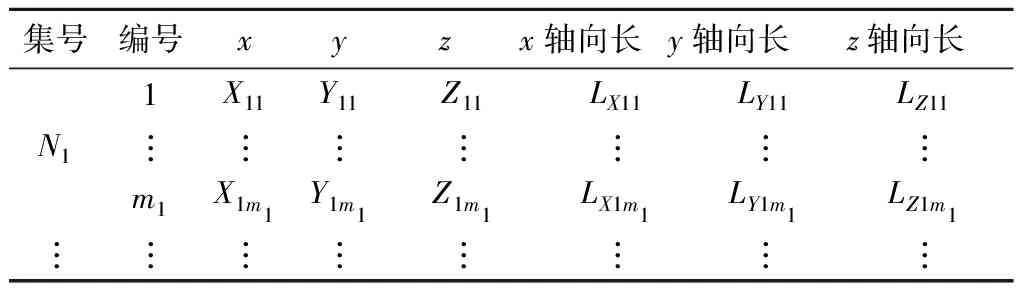
表5 器材布局位姿数据信息Tab.5 Layout information after optimization
3 实例
以某救援器材车器材布局为例:车辆为6×6全轮驱动,载重36 t,其箱体尺寸为7 360 mm×2 500 mm×2 250 mm;依据消防救援车辆标准、桥荷载重以及行车稳定性要求得出合重心高度<1 800 mm(底盘车架高度为1 400 mm),横向偏移中心<150 mm,纵向坐标范围在3 000 mm~3 300 mm;装载器材装备为8类,共120种700件.根据器材信息建立如表1的几何数据,并分析得出其关系矩阵.根据所提出的模型和算法,运用Matlab进行计算,快速得出器材的布局方案(见图3);并输出优化目标值,器材的合重心坐标值、有效容积率等(见表6).
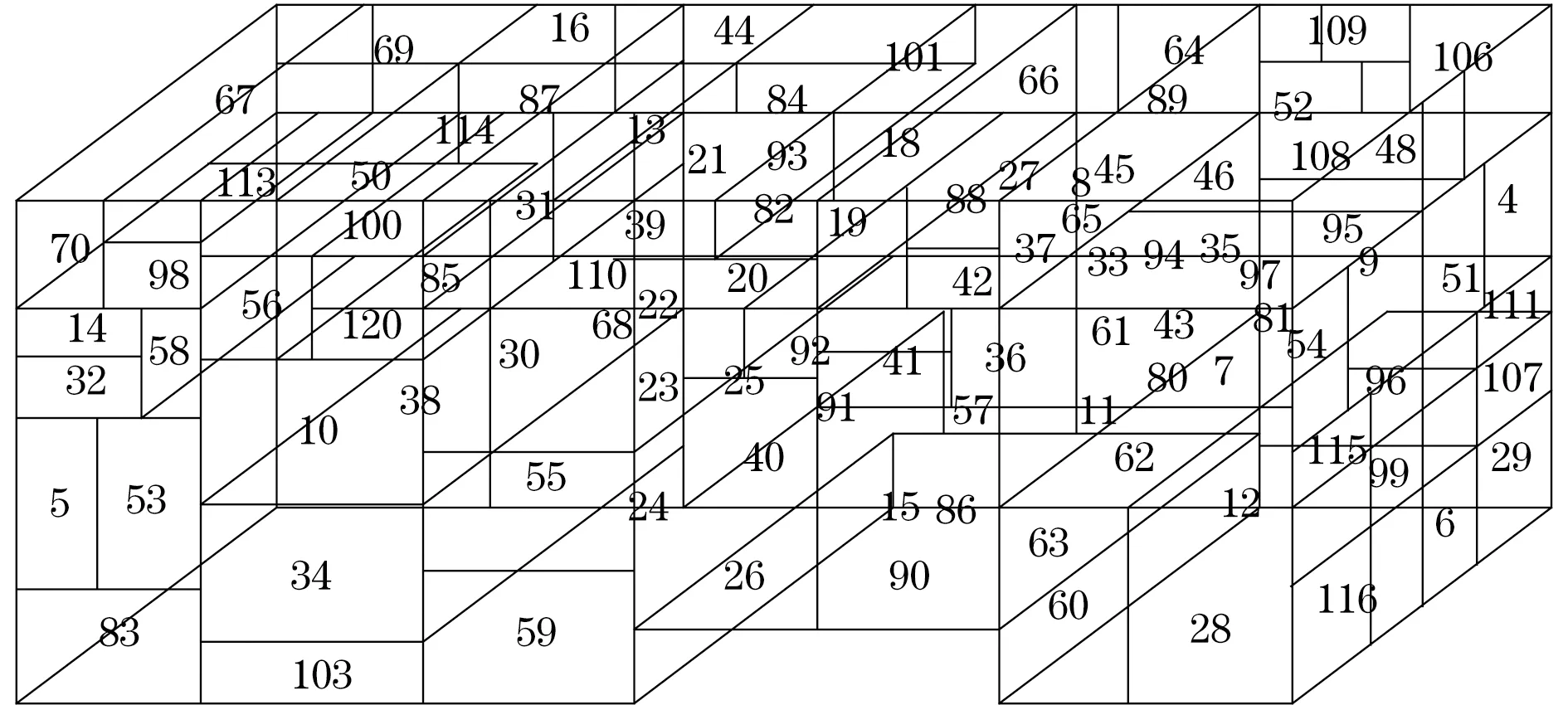
图3 布局方案示意图Fig.3 Sketch map of layout scheme

表6 优化目标值Tab.6 Optimal value generated from proposed model
从图3可以看出,关系度>1器材放置相对集中,质量重的器材布置下方区域,质量轻的器材布置于中上方区域,使用频率高的布局在箱体外层.以上说明布局方案符合布局规则.从表6中可以看出,合重心的坐标皆在要求范围内,箱体有效容积率高达85%.综上所述,利用该方法得到的器材布局方案既符合布局原则,又达到了优化目标,布局方案合理且优良.
4 结语
针对现有救援车辆器材布局设计的经验式定性设计方法存在主观性较强、缺乏科学性的问题,提出了基于启发式算法的器材布局快速设计方法.通过分析人与器材以及器材与器材关系,将设计人员的主观经验转化为定量分析的关系矩阵,并将器材布局需解决的空间利用率最大化、平衡布局(保证重心位置)要求转化为目标函数,利用器材布置原则得出先外层后内层的布局策略,最终得出布局方案.通过实例验证,该方法为器材布局提供了一种快速、可行并有效的定量化设计方法,但在布局策略和约束定义方面仍存在不足,对于复杂的箱体表达、数学模型及布局策略优化还要进一步研究和探讨.
参考文献:
[1] 姚澜,王小平,陈晓冉.基于系统分析的特种车辆器材布局设计研究[J].科学技术与工程,2012,12(4):734-748.
YAO L,WANG X P,CHEN X R.Research on equipment layout design of special vehicle based on system analysis[J].Science Technology and Engineering,2012,12(4):734-748.
[2] 刘小霞,王小平,杨延璞.基于人机工程学的消防车器材布局优化设计研究[J].图学学报,2012,33(5):109-113.
LIU X X,WANG X P,YANG Y P.Optimization and research of fire fighting truck layout design based on ergonomics[J].Journal of Graphics,2012,33(5):109-113.
[3] 沈健,陈俊,秦辉.基于人因工程的特种车辆设备布局设计方法研究[J].机械设计与制造,2015(12):216-220.
SHEN J,CHEN J,QIN H.The optimized layout design of special vehicle based on ergonomics[J].Machinery Design and Manufacture,2015(12):216-220.
[4] 姚怡.二维装箱问题的启发式算法研究[D].广州:华南理工大学,2016.
YAI Y.Research on two-dimension bin packing problem of heuristic algorithms[D].Guangzhou:South China University of Technology,2016.
[5] 周娜,舒帆,金佩卿.基于混合启发式算法的设备混合布局问题[J].工业工程,2017,20(1):77-82.
ZHOU N,SHU F,JIN P Q.Facility mixed layout problems(FMLP)based on hybrid heuristic algorithms[J].Industrial Engineering Journal,2017,20(1):77-82.
[6] 王露.基于聚类和区域寻优的零部件排版启发式搜索算法研究[D].湘潭:湘潭大学,2016.
WANG L.Study on the heuristic search algorithm based on clustering and region positioning for the component nesting problem[D].Xiangtan:Xiangtan University,2016.
[7] 郝亮.卫星舱组件分配与布置的集成布局方法[D].南京:南京信息工程大学,2016.
HAO L.Integrated layout methods for satellite module component distribution and layout[D].Nanjing:Nanjing University of Information Science and Technology,2016.
[8] 何良莉,魏发远,王峰军.一种基于FOB的人机交互式装填布局方法[J].机械设计与制造,2009(3):29-31.
HE L L,WEI F Y,WANG F J.A method based on flock of birds with human-computer technology for packing layout[J].Machinery Design and Manufacture,2009(3):29-31.
[9] 雷定猷,汤波,张英贵,等.一车多件货物装载布局优化模型与算法[J].铁道学报,2011,33(9):1-9.
LEI D Q,TANG B,ZHANG Y G,et al.Optimizing model and algorithms of loading and packing multi-piece freights into one car[J].Journal of the China Railway Society,2011,33(9):1-9.

