基于改进粒子群算法的高校排课问题优化

罗义强 陈智斌(昆明理工大学理学院 云南 昆明 650500)

0 引 言

高校课程编排是一项分配时间和空间给课程同时满足一定约束的活动。很多教育机构的课程编排系统没有完全自动化，需要一定的人工辅助。主要是因为课程编排的组合性和动态变化性。课程编排是计算机科学(CS)、运筹学(OR)、人工智能(AI)等领域的一个比较重要和带有挑战性问题。课程编排可以建模化为约束满足问题(CSP)对待。约束满足问题是组合优化问题并且被证明是NP-complete的[1]。搜索空间庞大并随变量指数级增长使得大多数NP-complete问题难以有效和优化地求解。

高校课程编排被大量的学者进行了广泛的研讨。各种各样的方法被提出去求解高校课程编排问题。这些方法包括：图着色[2]，将高校课程编排问题转化为一个图，顶点代表课程，边代表约束。颜色的数目相当于可行的时间档。图着色法分配有限的颜色给顶点，没有被一条边联结的相邻两个顶点同一种颜色。遗传算法(GA)[3]，以基因编码课程编排限制，以惩罚函数评估课程满意度。线性规划[4]、模拟淬火算法(SA)[5]、禁忌搜索算法(TS)[6]等。这些算法的不足之处是难以处理课程编排过程的约束，只能产生可行解，结果令人难以满意。

一些研究表明混合算法在解决高校课程编排问题显示出有前景的结果。整合局部搜索算法(LS)到粒子群算法(PSO)中，构建了高校课程编排的最优解[7]。约束传播与遗传算法相融合，得到了高校课程编排的近似最优解。遗传算法的不足之处是计算耗时长。粒子群优化算法与遗传算法相比，收敛速度比较快，并且不需要过多的参数调整[8]。单纯的PSO不能解决约束满足问题[9-11]。课程编排问题属于约束满足问题，所以需要寻找一种方法处理控制课程编排问题中的约束冲突。

本文提出一种经过改进的基于粒子群算法的算法(粒子群- 前行检测算法(PSO-FC))，即将前行检测算法(FC)融合到粒子群算法(PSO)中。粒子群算法产生课程编排的潜在解，前行检测算法优化这些潜在解。

1 高校课程编排问题

课程编排涉及时间档(T)、教室(R)、教师(I)和课程(S)等因素。表1展示了某高校每周课程表的结构。每天有11个时间档，一周上课5天，每周总共55个时间档，除去为特别事件(午餐、午休、会议等)预留的12个时间档。用于课堂教学的时间档共43个。

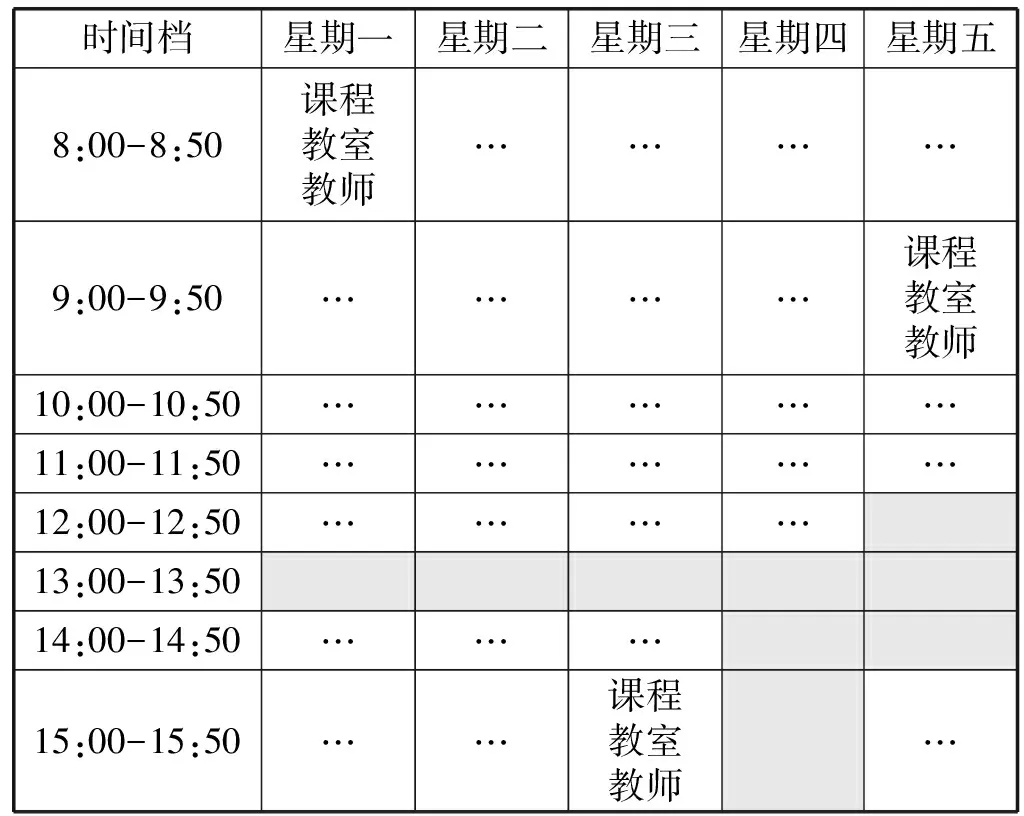
表1 某高校每周课程表结构示例

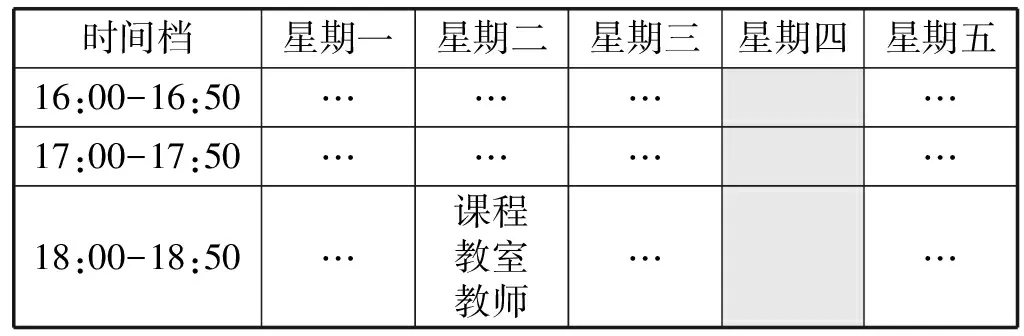
续表1

为特别事件预留的时间档

1.1 建模高校编排问题为约束满足问题

约束满足问题是决策问题，定义为一组对象的状态必须满足一定数量的约束。

一般地，约束满足问题由变量、定义、约束条件构成。约束满足问题形式为P=(X,D,C)，其中：

•X={X1,X2,…，Xn}表示变量集。

•D={D1,D2,…，Dn}表示定义域集，Di为分配给变量Xi的有限可能数值。

•C={C1,C2,…，Cm}表示约束集，表示变量之间的关系，Ci⊆{Di1×Di2×…×Dik}。

很多约束满足问题算法是基于搜索和推理的原则的。搜索法、推理法的代表分别为回溯算法(BT)、兼容性强化技术。前行检测算法是常见的一种兼容性强化技术。搜索法是为一般应用而开发的，不使用约束来提高效率。相反，兼容性强化技术使用约束缩减搜索空间直到找到解。单独应用搜索或兼容性强化技术都不能有效地解决约束满足问题。所以，结合搜索法和兼容性强化技术，可以发挥两者的优势，缩减搜索空间，加快搜索进程。

约束满足问题的可行解通过实例化满足所有约束条件的变量得到。给定目标函数，通过实例化满足所有约束条件的所有变量并优化给定的目标函数来找到最优解[12-15]。

课程编排问题中，变量为课程Si，定义域为可行的时间档T(Si)和教室R(Si)，约束C(Si)为变量之间的关系。课程编排问题的解可以定义为分配时间T(Si)和教室R(Si)给教师I(Si)讲授的课程Si并满足一定的约束C(Si)。课程编排问题可以定义为4-元组[Si,T(Si),R(Si),C(Si)]的约束满足问题。

1.2 课程编排的约束

约束在构筑可行和优化的课程表方面起着重要作用。

1) 分配给课程的时间档和教室必须从时间档和教室定义域中选择。

(∀i)∃(t∈T(Si))(δi=t)

(1)

(∀i)∃(r∈R(Si))(εi=r)

(2)

分配给课程i的时间档和教室分别以δi和εi表示。

2) 某位教师讲授多门课程，在同一时间档内，一位教师不能分配多于一门课程的教学。

∀(I(Si)=I(Sj))∃(T(Si)≠T(Sj))

(3)

课程Si和课程Sj的上课时间不能相同，因为是同一位教师授课。

3) 一个学生群在同一时间档不能分配参与多门课程的学习。

∀(G(Si)=G(Sj))∃(T(Si)≠T(Sj))

(4)

课程Si的上课时间T(Si)不能与课程Sj的上课时间T(Sj)相同，因为它们属于同一学生群，即G(Si)=G(Sj)。

4) 一间教室在同一时间档内不能分配给多门课程使用。

∀(R(Si)=R(Sj))∃(T(Si)≠T(Sj))

(5)

5) 教室能容纳的学生数目应该不少于上课学生人数。

∀(R(Si)=rk)∃(Z(R(Si))≥N(Si))

(6)

Z(R(Si))为分配给课程Si的教室R(Si)的容量，N(Si)为课程Si的上课学生人数。

6) 某些时间档预留给特别事件E，例如对时间档有特定要求的教师。

∀(tj=E)∃(T(Si)≠tj)

(7)

7) 某些教室预留给特定事件F，例如对教室有特定要求的教师。

∀(rj=F)∃(R(Si)≠rj)

(8)

2.1 粒子群算法

粒子群算法(PSO)是Kennedy和Eberhart受鸟群运动模型启发而提出的随机群体搜索算法。粒子群算法将鸟群运动模型中的栖息地类比为问题解空间中可能解的位置，将解空间中的每只鸟类比为每个候选解，称之为粒子。由随机初始化形成的粒子组成一个种群，种群中的粒子在解空间中以一定的速度飞行。粒子通过适应度函数对两个极值进行评估，更新速度和位置。第一个为个体极值，即目前粒子本身发现的最佳位置。第二个为全局极值，即整个种群中目前找到的最佳位置。通过粒子间的相互协作和信息共享，以迭代的方式进行搜索直至达到规定的迭代次数或满足规定的误差标准为止，进而得到最优解。详细的粒子群算法见算法1。

假设在一个D维的目标搜索空间中，有M个粒子组成一个种群，其中第i个粒子在D维空间中的位置为xi=(xi1,xi2,…,xid)，第i个粒子的速度vi=(vi1,vi2,…,vid)，记第i个粒子的个体极值pi=(pi1,pi2,…,pid)，整个种群的全局极值为g=(g1,g2,…,gd)，则粒子根据下式进行速度和位置的更新：

(9)

(10)

(11)

式中：d=1,2,…,D;i=1,2,…,M；c1和c2为学习因子，取值范围是非负常数；r1和r2是介于之间的随机数；χ为伸缩因子，用于控制速度的惯性，φ=c1+c2，φ>4通常φ取4.1，χ取0.729 84[16-19]。

算法1粒子群优化算法。

Procedure of PSO

1 for each particle i=1,2,…,S do

2 Initialize the particle’s position with a uniformly distributed random vector: xi∈U(blo,bup)

// bloand bupare respectively the lower and upper boundaries

//of the search-space

3 Initialize the particle’s best known position to its initial position: xi←pi

4 if f(pi)>f(g) then

5 update the swarm’s best known position: g←pi

6 Initialize the particle’s velocity: vi∈U(-|bup-blo|,|bup-blo|)

7 while a termination criterion is not met do:

8 for each particle i=1,2,…,S do

9 for each dimension d=1,2,…,N do

10 Pick random numbers: r1,r2～U(0,1)

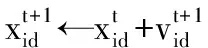
13 if f(xi)>f(pi) then

14 Update the particle’s best known position: pi←xi

15 if f(xi)>f(g) then

16 Update the swarm’s best known position: g←pi

17 Return the particle with the best fitness value of all as

2.2 粒子编码

使用直接编码的方案。每个粒子包含关于课程的时间档和教室信息。粒子的编码结构形式为P[Si;Tj;Rk]。i=1,2,…,N;N为课程数目的最大值。j=1,2,…,M;M为时间档的最大数目。k=1,2,…,P;P为教室的最大数目。特别地，若某些课程有平行班要求同步安排时间，则重复构造出规定数量的粒子，形成初始粒子群。

2.3 前行检测算法

前行检测算法是一种基于回溯的算法。回溯算法是解决约束满足问题的基本方法。回溯算法的基本思想是：在问题的解状态空间树中，依深度优先方式(DFS)遍历，不断地尝试为未分配变量反复选择数值，将局部解扩展到全局解。回溯算法由根节点出发进行搜索，对于解状态空间树的某个节点，若该节点满足问题的约束，则进入该子树继续进行搜索，否则将以该节点作为根节点的子树进行剪枝，逐层向根节点进行回溯，直至根节点的所有子树都搜索完毕。回溯算法适用于组合数较大的问题。

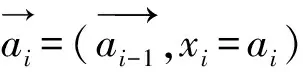
算法2前行检测算法

Procedure of FC

输入：约束问题P=(X,D,C)

输出：解或无解。

//复制定义域

2 i←1

//初始化计数

3 while 1≤i≤n

4 instantiate xi←SELECT-VALUE-FC

5 if xiis null

//无值返回

6 i←i-1

//backtrack回溯

8 remove any constraints added since xiwas last instantiated

9 else

10 i←i+1

//step forward前向

11 end while

12 if i=0

13 return inconsistent

14 else

15 return instantiated values of {x1,…,xn}

16 end procedure

算法3前行检测算法的选取数值子算法

Subprocedure of SELECT-VALUE-FC

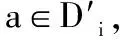
3 empty-domain←false

4 for allk,i≤k≤n

//约束cm检测

8 end for

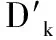
//xi=a leads to a dead-end一些未来变量域为空

10 empty-domain←true

11 end for

12 if empty-domain

//不选 a

14 else

15 return a

16 end while

17 return null

//无兼容值

18 end procedure

2.4 粒子群前行检测算法

粒子群算法具有通过更新粒子飞行位置和速度结合适应度函数寻找优化解的能力。单纯使用粒子群算法不能解决诸如约束满足问题这种复杂问题。这是粒子群优化算法的本性所致，粒子群优化算法设计用于寻求通过更新粒子飞行位置和速度结合适应函数的可能解，但它不能处理约束。所以，需要寻找一种能够处理约束的技巧。整合前行检测算法到粒子群算法中，得到粒子群- 前行检测算法(PSO-FC)，对课程编排问题的约束能进行优化。

粒子群- 前行检测算法分两阶段。第一阶段执行粒子群优化算法，这个阶段产生潜在解分配教室和时间档给课程。搜索空间的大小由教室和时间档决定。例如，教室数目为15，时间档数目为20，则搜索空间大小为15×20=300。

限定搜索空间的规模，粒子就不能逃逸到搜索空间之外。每个粒子将通过与邻近粒子共享与交换信息结合适应函数更新教室和时间档。

第二阶段应用前行检测算法。为了便于搜索解，将课程编排问题罗列成树图的组织结构，如图1所示。树的层次对应于教室Rk和时间档Tj。这个阶段用于验证第一阶段产生的潜在解的兼容性。兼容性测试的目的是决定定义域取出的数值是否与相关的约束抵触。若不兼容，数值将会从定义域移除。定义域的每个变量值代表搜索空间的一个节点，移除定义域中的数值意味着搜索空间的减小。这样有利于加快运算的速度。检测学生群与教师对课程的可行性，教室是否够大可以容纳上课的学生数，教室和时间档对课程是否兼容。当第一阶段产生的潜在解与约束抵触时，前行检测算法就会启动，验证教室Rk、时间档Tj和当前课程Si的兼容性，寻找有效的解加以修复。若找到可行的教室和时间档，分配给课程。否则将会回溯到其他可行的教室和时间档。前行检测算法在潜在解有效性验证遇到标记符号“0”执行，当遇到标记符号“1”，接受潜在解。其中“0”表示潜在解与约束抵触，“1”表示潜在解与约束不抵触。图2显示了粒子群- 前行检测算法的流程概览。图3显示了粒子群- 前行检测算法进行约束处理的例子。

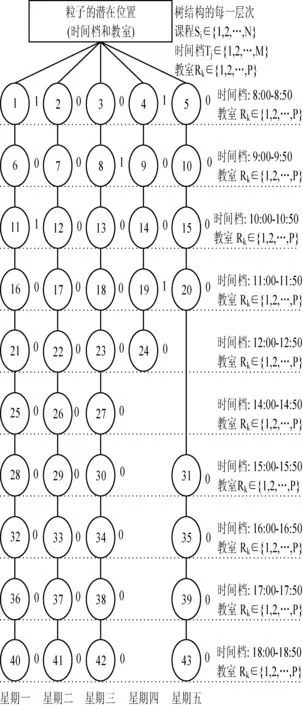
图1 前行检测的解状态空间树结构图

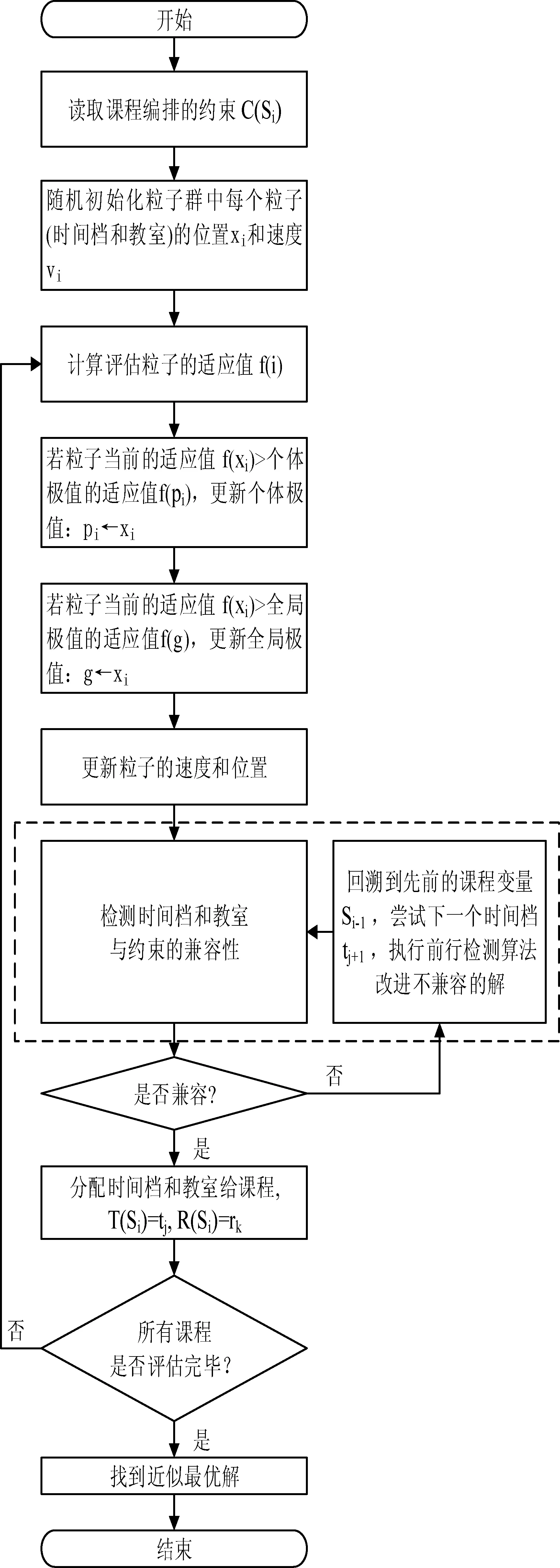
图2 粒子群- 前行检测算法流程概览

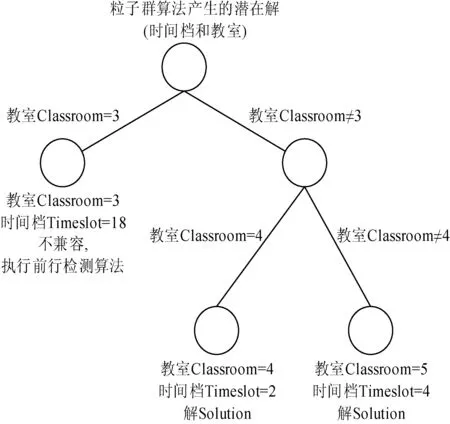
图3 粒子群- 前行检测算法约束处理示例

2.5 适应度函数

课程编排的主要目标是找到一个近似最优的课程表，优化利用好资源(时间和教室)。适应度函数的作用是对教室和时间档的偏好值的排序进行优化，最大化时间档和教室的偏好值。此处的偏好值是教师基于时间档和教室的可利用性和便利性而对时间档和教室赋予的权重。通过对教室和时间档排序，偏好值可以被确定。最好的教室和时间档赋予最高的偏好值。使用这样的适应度函数，最好的教室和时间档会分配给课程。满足这样条件的解称之为近似最优解。适应度函数表示为：

(12)

式中：P(T(Si))是教师I(Si)对时间档(课程Si对应的时间档)的偏好值，P(R(Si))是教师I(Si)对教室(课程Si对应的教室)的偏好值，其中i=1,2,…,n。

2.6 变量和变量赋值排序

变量(课程)和变量赋值(时间档和教室)排序在约束满足问题中很重要，因为它们直接关系到粒子群- 前行检测算法中搜索的有效性和解的可行性。它们可以减少搜索的空间，快速地寻找到问题的解。排序依据特定的偏好执行，这样在任何时间可以扩展最好的结点，引导找到最优解。

设S1,S2,…,Sn为一系列课程变量，根据以下的标准进行排序为S1≤S2≤…≤Sn。

• 课程的重要性和关键要求。

• 课程难易程度。

结点扩展取决于序列中的变量赋值选取。根据下面的标准对时间档T1,T2,…,Tm进行排序为T1≤T2≤…≤Tm。

• 一天之中时间档的位置。

• 与一周起始第一天的距离。

教室R1,R2,…,Rk基于以下的标准顺序排列为R1≤R2≤…≤Rk。

• 教室的设施，空调，噪声。

• 离中心活动区的远近。

• 楼层的高度。

• 教室的容量最接近上课学生人数

3 实验结果分析

粒子群- 前行检测算法在2 GB RAM， Core 2 Duo 2.2 GHz CPU，Windows 7，Visual C++2008的微机环境进行。提出的算法使用某高校数学与信息系统学院的数据进行了测试。粒子群算法参数设置如表2所示。表3给出了课程编排的基本信息。表4和表5给出了时间档和教室偏好值的信息。

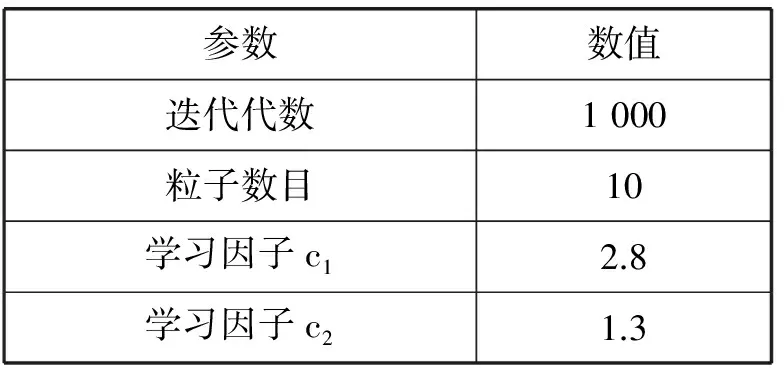
表2 PSO参数设置

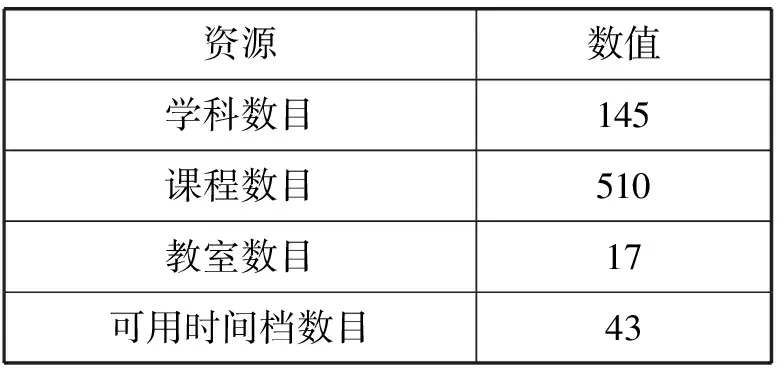
表3 课程编排基本信息概要

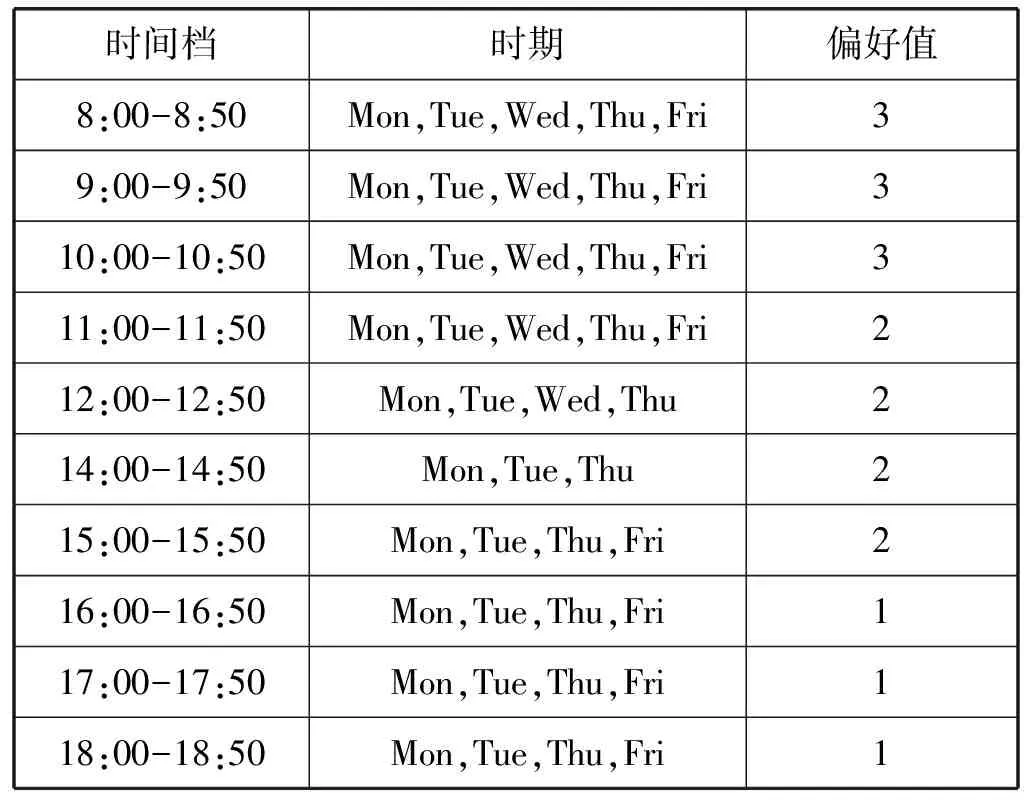
表4 高校教师对时间档的偏好值概要

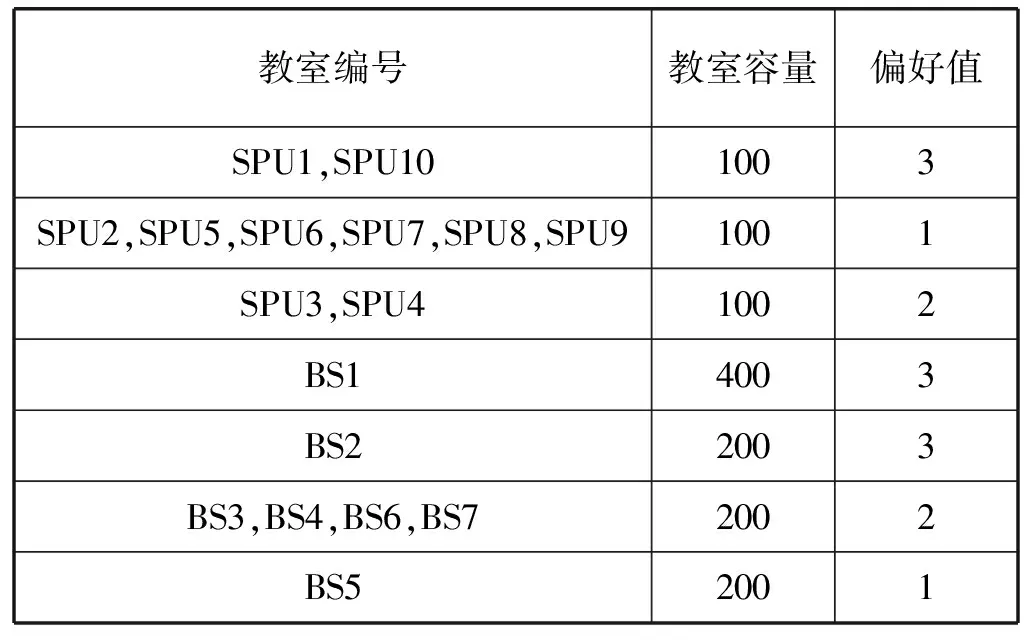
表5 高校教师对教室的偏好值概要

为了评估粒子群- 前行检测算法(PSO-FC)的课程编排的性能，将它与标准粒子群优化算法(PSO)[21]和整合局部搜索的粒子群算法(PSO-LS)[8]进行了对比。每种算法独立运行5次，实验结果见表6-表8。

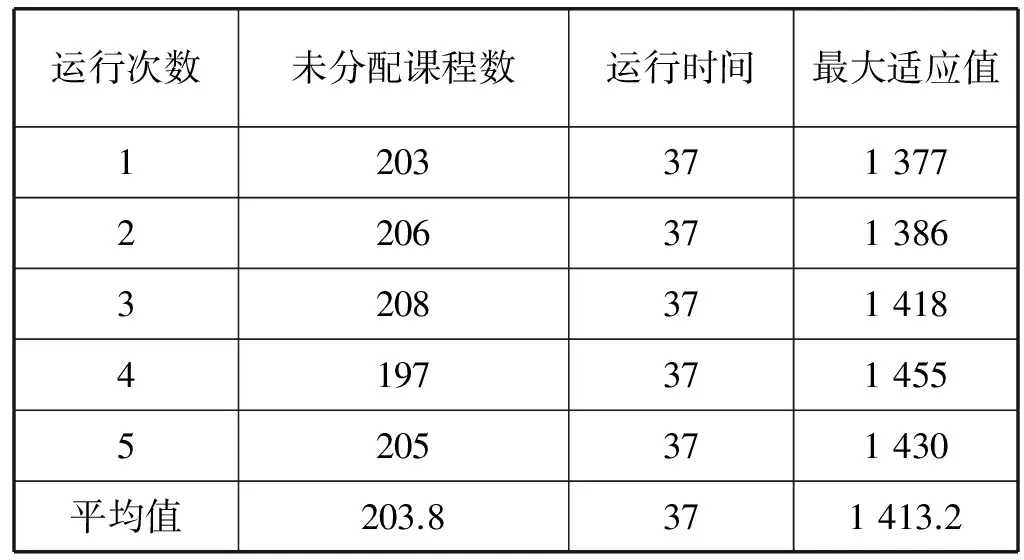
表6 标准PSO运行5次的结果

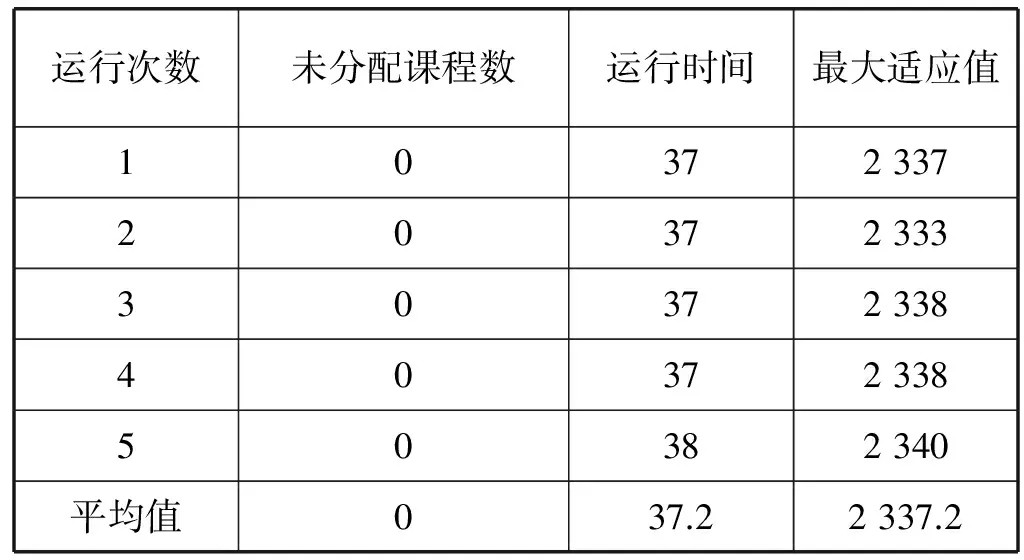
表7 PSO-LS运行5次的结果

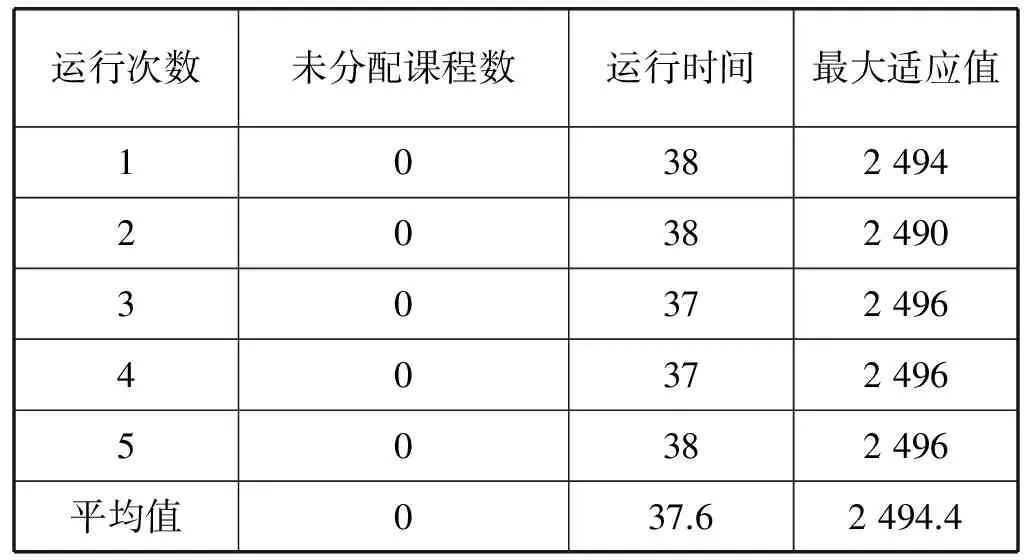
表8 PSO-FC运行5次的结果

由表6-表8得出，三种算法都能产生课程编排的可行解。平均运行时间耗费方面，三种算法相差不大。但通过查看表8中平均适应值的最大值，与表6和表7中的相应值进行对比，适应值(教师对教室和时间档的偏好值)是最大的。这表明PSO-FC算法能产生可行近似最优解，解的质量最好。

与标准PSO算法和PSO-LS算法相比，PSO-FC算法产生解的时间耗费稍微长一些。因为需要验证可能解的有效性和遇到无效解产生时的回溯搜索。标准PSO算法和PSO-LS算法可以更快地生成解，因为两者接受任何一个与约束不抵触(没有最大化偏好值)的解且不进行任何回溯过程，所以两者产生的解为可行解。单纯使用PSO算法余下一些未分配的课程，因为它不能处理课程编排过程的约束。这些未分配的课程最终还需要人工编排。人工编排耗时长，效率不高。

综上所述，标准PSO算法、PSO-LS算法和PSO-FC算法都能应用于实际的课程编排。综合考虑运行时间和适应值两方面因素，PSO-FC算法优于标准PSO算法各PSO-LS算法，更能满足实际课程编排的需求。

4 结 语

本文提出了一种将前行检测算法融合到粒子群算法(粒子群- 前行检测算法)来解决高校课程编排问题的方法。为了验证算法的性能，与整合局部搜索的粒子群算法和标准粒子群算法进行了比较分析。使用粒子群- 前行检测算法在解决高校课程编排问题的过程中，教师对教室和时间档的偏好值在选择的适应度函数的作用下得到了最大化。粒子群- 前行检测算法中的前行检测阶段对粒子群算法阶段产生的解进行了验证，当遇到无效解时就通过约束处理来寻找有效的解。前行检测算法能够显著地减少搜索空间。实验表明，所有方法都提供可行解，但粒子群- 前行检测算法给出了近似最优解。未来的研究工作将专注于试验不同的约束满足问题个案进一步验证所提出的算法的性能。

[1] Kingston J H. Timetable construction: the algorithms and complexity perspective[J]. Annals of Operations Research, 2014, 218(1):249- 259.

[2] Hiryanto L. Incorporating dynamic constraint matching into vertex-based graph coloring approach for university course timetabling problem[C]//Proceedings of 2013 International Conference on QiR,USA: IEEE, 2013: 68- 72.

[3] Alves S S A, Oliveira S A F, Neto A R R. A novel educational timetabling solution through recursive genetic algorithms[C]// Computational Intelligence. IEEE, 2016: 1- 6.

[4] Fonseca G H G, Santos H G, Carrano E G, et al. Integer programming techniques for educational timetabling[J]. European Journal of Operational Research. 2017, 262:28- 39.

[5] Tarawneh H Y, Ayob M, Ahmad Z. A Hybrid Simulated Annealing with Solutions Memory for Curriculum-based Course Timetabling Problem[J].Journal of Applied Sciences, 2013, 13(2): 262- 269.

[6] Lüaba Z. Adaptive Tabu Search for course timetabling[J].European Journal of Operational Research, 2010, 200(1): 235- 244.

[7] Deris S, Omatu S, Ohta H, et al. Incorporating constraint propagation in genetic algorithm for university timetable planning[J]. Engineering Applications of Artificial Intelligence, 1999, 12(3): 241- 253.

[8] Ho I S F, Deris S, Zaiton M H S. A Combination of PSO and Local Search in University Course Timetabling Problem[C]//International Conference on Computer Engineering and Technology. IEEE Computer Society, 2009: 492- 495.

[9] Li H. Narrowing Support Searching Range in Maintaining Arc Consistency for Solving Constraint Satisfaction Problems[J]. IEEE Access, 2017, 5(99): 5798- 5803.

[10] Di M M, Forti M, Nistri P, et al. Nonsmooth Neural Network for Convex Time-Dependent Constraint Satisfaction Problems[J]. IEEE Transactions on Neural Networks & Learning Systems, 2016, 27(2): 295- 307.

[11] Luo T, Dolan M, Davidson E, et al. Assessment of a new constraint satisfaction problem based active demand control approach to address distribution network constraints[J]. ET Generation, Transmission & Distribution, 2015, 9(15): 2363- 2373.

[12] Jiang X, Cui P, Xu R, et al. An action guided constraint satisfaction technique for planning problem[C]//International Conference on Cognitive Informatics & Cognitive Computing. IEEE, 2017: 167- 173.

[13] Shen J, Mei D. The Freuder Width in a General Model of Constraint Satisfaction Problem[C]//International Symposium on Computational Intelligence and Design. IEEE, 2017: 303- 306.

[14] Chen H, Valeriote M, Yoshida Y. Testing Assignments to Constraint Satisfaction Problems[C]//Foundations of Computer Science. IEEE, 2016: 525- 534.

[15] Rouahi A, Salah K B, Ghydira K. Belief Constraint Satisfaction Problems[C]//Computer Systems and Applications. IEEE, 2016: 1- 4.

[16] Mallick S, Ghoshal S P, Acharjee P, et al. Optimal Static State Estimation Using hybrid Particle Swarm-Differential Evolution Based Optimization[J]. Energy & Power Engineering, 2017, 5(4): 670- 676.

[17] Jin H L, Song J Y, Kim D W, et al. Particle Swarm Optimization Algorithm with Intelligent Particle Number Control for Optimal Design of Electric Machines[J]. IEEE Transactions on Industrial Electronics, 2018, 65(2): 1791- 1798.

[18] 项铁铭, 王建成. 改进的多目标粒子群优化算法[J]. 计算机应用与软件, 2017, 34(9):302- 305.

[19] Tassopoulos I X, Beligiannis G N. Solving effectively the school timetabling problem using particle swarm optimization[J]. Expert Systems with Applications, 2012, 39(5): 6029- 6040.

[20] Dechter R, Frost D. Backjump-based backtracking for constraint satisfaction problems[J]. Artificial Intelligence,2002, 136(2): 147- 188.

[21] Irene S F H, Deris S, Zaiton M H S. A Study on PSO-Based University Course Timetabling Problem[C]//International Conference on Advanced Computer Control. IEEE Computer Society, 2009: 648- 651.