基于红外热成像技术的水力发电机效率的测定方法

(华东宜兴抽水蓄能有限公司，江苏 宜兴 214205)

1 概 述

发电机的能量转换效率的实际测定对于制造厂家和电力公司来说都是至关重要的，所测定的发电机效率是设计优化和验收测试的重要指标[1]。此外，发电机效率也说明了能源转换的过程，可以作为指导发电机运维的良好阈值[2]。

任何能量转换系统的效率都是该系统的输出和输入之间的关系。这一基本概念构成了直接效率测试方法的基础，即测量输入和输出功率并相互关联。输入功率和输出功率之间的差异会导致能量损耗，这是任何能量转换系统固有的。能量损耗的确定是间接能量测试方法的核心[3-4]。只要由输入功率可以得到输出功率与功率损失的总和,效率η是可以计算得出的。对于水力发电厂的同步电机，由于输入功率是机械性质的，因此，输出功率的测量比输入功率要简单[5-6]。

采用直接方法测量大型水力发电机组的输入功率和输出功率，由于水力发电机组的输入、输出功率值较大，将会出现不可避免的测量误差，导致结果的高度不准确性[7]。

由于直接测量水力发电机效率存在较大困难，因此采用间接法测量水力发电机效率的方法得到大力发展。间接方法的优点是只测量一个较大的输出功率和一个相对较小的损耗功率。只要损失测定中所涉及的误差按比例减少，最终得到的功率测量的总体不确定性就会降低[8-9]。

水力发电机组的热损耗主要有冷却液吸收的热损耗、机组表面损失的热量。其中从水力发电机组表面传到外部环境的热辐射、从机组传到混凝土外壳的热对流以及从传动轴热传导损失的热量占到总体热量损耗的约10%[10]。这部分热量测量目前主要通过接触式温度传感器测定。此外通过传动轴热传导损失的热量由于测量难度大，目前，被大部分现场效率测定程序所忽略[11]。

文献[12]通过应用量热法测定小型电机的损耗量的试验，开发出同步电机的一些损耗理论模型，试验结果与测试结果一致。然而之前的量热法研究都基于大量的温度传感器实现对水力发电机的热量损耗监测，这种方法存在系统造价高、高度依赖温度传感器、运行可靠性低等问题。此外在现场测定水力发电机效率由于需要设置大量温度传感器，需要耗费大量人工，测量效率较低。

基于上述考虑，本文在应用量热法来确定现场水力发电机组的能量转换效率的基础上，引入红外热成像技术用于测定热量损耗。该测量方法通过非接触式热成像仪测量机器表面温度，通过传热系数的计算获得发电机组的热量损耗。该方法还能够对发电机传动轴的导热损失进行测定，提高了发电效率的测量精度。

2 量热法原理

量热法理论的依据是所有的机器损耗都转化为热能[13]。因此，如果可以建立涉及发电机组的热量损耗模型，就可以通过观察到的热量交换来确定所有的热能损耗。

图1描述了水力发电机组的冷却剂流体(如空气、水)和冷却油与外部环境的热交换，以及它们的输入温度和输出温度。辐射对流的热量流失也在图1中标识出来。如果这样的控制量真的可以在机器周围构建，更适合于小尺寸的，那么这个想法是可行的。

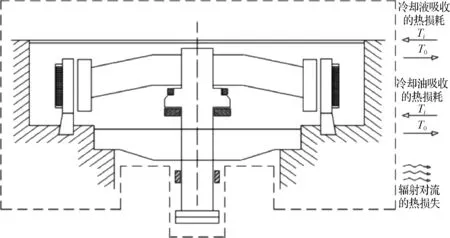
图1 水力发电机组的热量交换示意图

对于大型水力发电机组来说，如果对每个机组热能损耗分别计算传热，则会更容易得出热量损耗值。损耗与用于发电机组内部零件的冷却剂流体(例如空气和水)以及轴承的油温升高成比例。通过机器表面流向混凝土和环境的热量也应该被考虑进去[14-15]。下面基于主要途径的热能损耗进行详细计算。

2.1 冷却液吸收的热损耗

这部分热损耗涉及冷却的机器，包括它们的部件，其中移动的介质在一个封闭的系统中循环。冷却液吸收机组热损耗的计算公式为

Plosses=cρQΔθ

(1)

式中Plosses——计算吸收损耗，kW；

c——热容量，kJ/(kg·K);

ρ——密度,kg/m3;

Q——体积流量,m3/s；

Δθ——升温,K。

与具体冷却液相关，表1列出了最常见的冷却液的典型值。

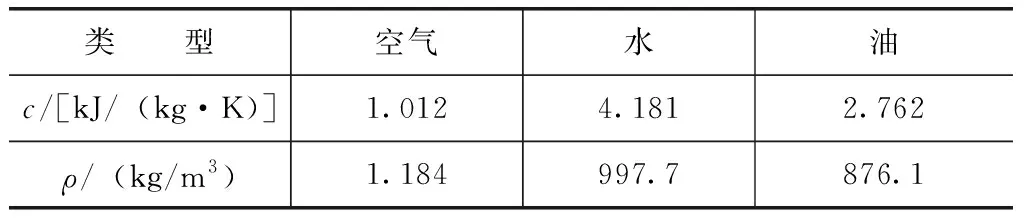
表1 典型的计算参数值(在300K)

一般来说，对于空气或水冷机器，用这种技术测定的损耗是内部损耗，包括机器导体的焦耳效应，机芯上的磁滞和涡流损耗，杂散负载损耗、摩擦和风压损失。对于分离的油冷却轴承，也可以使用相同的方法和相关的常数来确定任何导向轴承的损失。

冷却液体积流量可以通过多种方式获得。非浸入式超声波流量计由于其精度高并且易于使用而被广泛应用，能够满足量热法测量精度要求。

2.2 辐射、对流和传导释放的热损失

由于水力机组暴露在外部环境中的大面积表面的温度明显高于环境温度，因此，会通过辐射、对流和传导方式流失大量热量。

这些热量损耗包括从水力发电机组表面到环境的热量传递、传递到混凝土外壳以及通过机器轴传递的热量。辐射和对流损失的一般方程为

Plosses=hAΔθ

(2)

式中h——传热系数,W/(m2·K)；

A——辐射表面的面积,m2；

Δθ——表面和环境之间的温差,K。

根据相关标准，指定一个取决于冷却剂流体速度的传热系数：

h=11+3v

(3)

h=5+3v

(4)

式(3)和式(4)分别用于外表面和内表面，其中v是冷却剂流体速度(m/s)。

3 传热系数的计算方法

尽管已经有相关标准给出了传热系数测定的方法，但是已有的研究表明存在更适合的方法来确定其值，并能够提高所得测量结果的准确性。此外，红外热像仪表面温度测量新技术为量热法应用和表面损失测定提供了新方法，这种测量技术也需要更加精确的传热系数计算方法。

传热系数取决于几个物理特性，如表面几何形状、流体黏度、流速和热性能，因此本文提出的传热系数计算方法如下：

(5)

式中k——流体导热系数，空气的导热系数约为0.0271W/(m·K)；

L——与外界接触的表面周长的等效长度,m;

Nu——努塞尔数。

努塞尔数是对流的热传导系数比，并且它是格拉斯霍夫数Gr和普朗特数Pr乘积的函数：

Nu=α(GrPr)b

(6)

系数a和b的值取决于所研究的物体表面的等效长度以及Gr和Pr之间的乘积值。表2总结出了典型的目标物体的计算系数值。

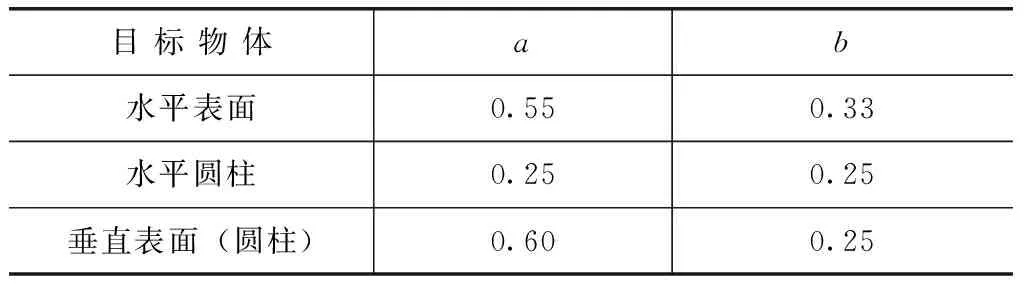
表2 a和b的典型系数值

Pr在空气中保持在0.7～0.8的范围内，Gr由下式给出:

(7)

式中g——重力加速度,m/s2；

v——流体运动黏度，空气的运动黏度是19.96×10-6m2/s；

Δθ——发电机表面温度和环境温度之间的差值；

θ——发电机表面温度和环境温度的平均值,K。

假定水力发电机表面温度为46℃，环境温度为32℃，将这些方程应用于水平轴涡轮水力发电机(假定为直径为3m、长度为8m的圆柱体)，计算得出传热系数为 12.79W/(m2·K)。对于直径为13.8m的水轮发电机，则计算出的传热系数为14.12W/(m2·K)。这些数值与IEEE std-115的数值非常接近，说明传热系数的计算方法可行。

4 温度测量

发电机表面温度和冷却剂的流体温度与水力发电机的负载和功率相关，这两个温度值的测定是确定发电机效率的关键问题。

如果使用温度传感器(如RTDs或热电偶)进行测量，温度读数是传感器所在的局部温度。冷却剂流体温度可从安装在适当的孔中的传感器获得，而发电机罩表面上的温度信息是从多个离散分布的温度传感器读数中计算得出的。

由于发电机表面的温度梯度引起的温度值变化可能导致温度传感器读数准确度降低，因此本文提出使用红外热像仪进行水力发电机表面温度的测量。

在绝对零度以上的每一个物体都因原子和分子的搅动而产生电磁辐射。搅动程度越高，其温度越高。根据斯蒂芬-波尔兹曼定律，一个物体的总发射辐射增长为其绝对温度的四次方：

M=εσT4

(8)

式中M——电磁辐射，W/m2；

T——绝对温度，K；

ε——物体表面辐射；

σ——斯忒藩-玻尔兹曼常数，其值等于5.6704×10-8W/(m2·K4)。

红外热像仪利用这一物理原理，通过检测加热体发射的电磁辐射来测量温度。红外热像仪的焦平面阵列(FPA)是一种由m×n个光学传感器组成的矩阵，用于将发射的辐射转换为温度映射。采用这种技术，能以非常高的精度测量温度，分辨率低于0.1℃。使用红外热像仪测得的水力发电厂同步发电机热成像图如图2所示。

4.1 热成像的视场跨度

热成像仪由一个热成像相机和相关的信号处理、显示系统组成。相机的视场(FOV)由相机镜头的光圈角决定，该镜头将物体图像投影到焦平面上。由图3可知，由两个笛卡儿方向的FOV值和从相机到目标物体表面的正交距离，可以确定热图像覆盖的物体区域：

(9)

(10)

式中d——由热成像仪到由H和V尺寸(m)定义的表面的正交距离;

FOVx、FOVy——视野在x和y方向的视场,(°)。

在FOV跨度范围内的损失是通过计算得到的:

Plosses=hHVΔθ

(11)

式中 Δθ——平均表面温度上升超过环境温度值，K。

考虑到与平面表面正交的视线，式(11)是有效的。然而从数学角度可以证明，对于典型视场角小于30°的情况，结果对于正交角度低于20°的视角偏差仍然有效。

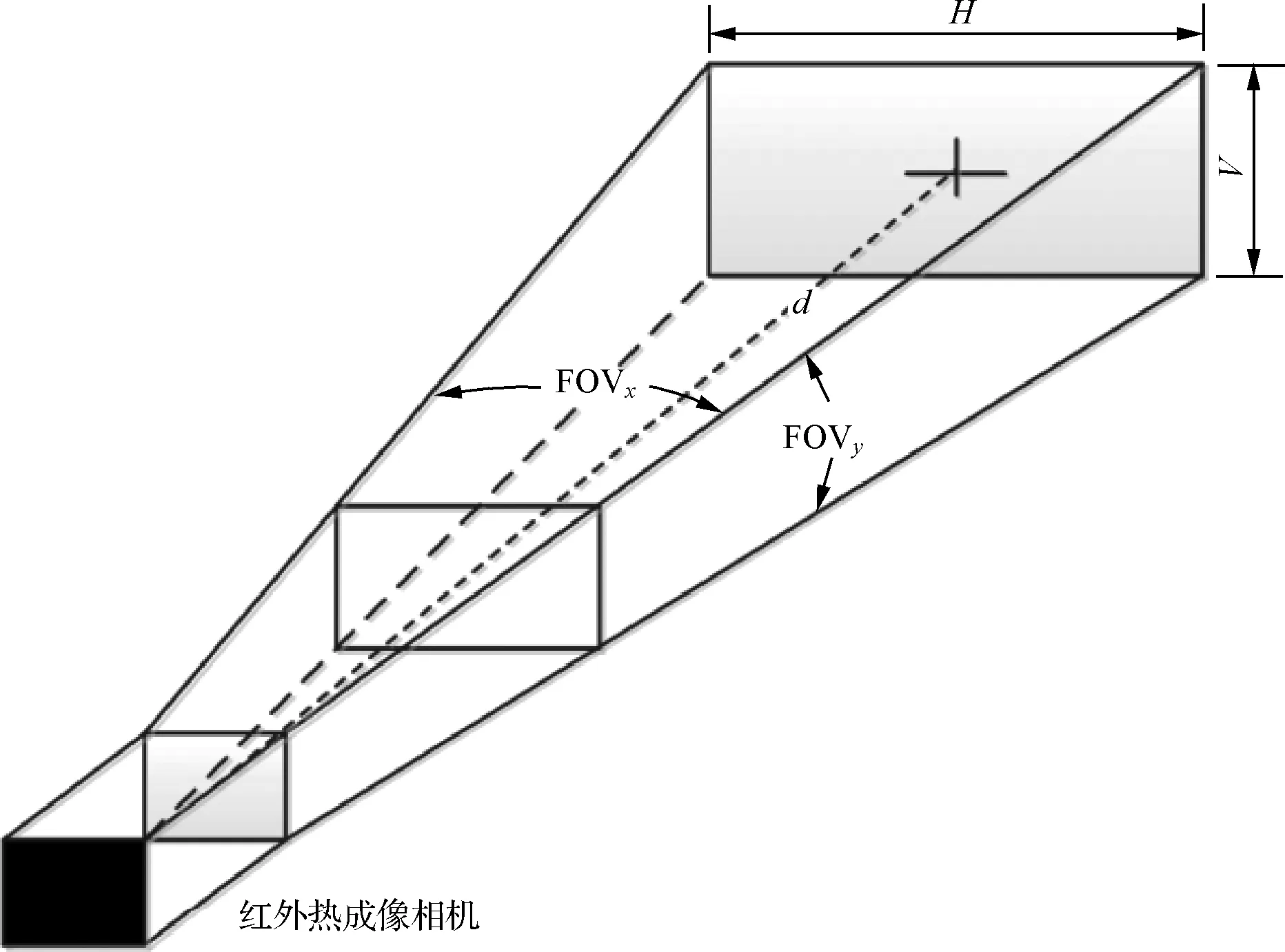
图3 热成像仪相机FOV和覆盖区域

4.2 等温线图

温度测量的另一种方案以及相关区域的确定是等温线中整个热表面的分割。

等温线技术包括建立一个温度范围，并将原始热图像中的所有像素映射到指定范围内的温度。

图4显示了一个水力发电机的表面热成像和等温线。

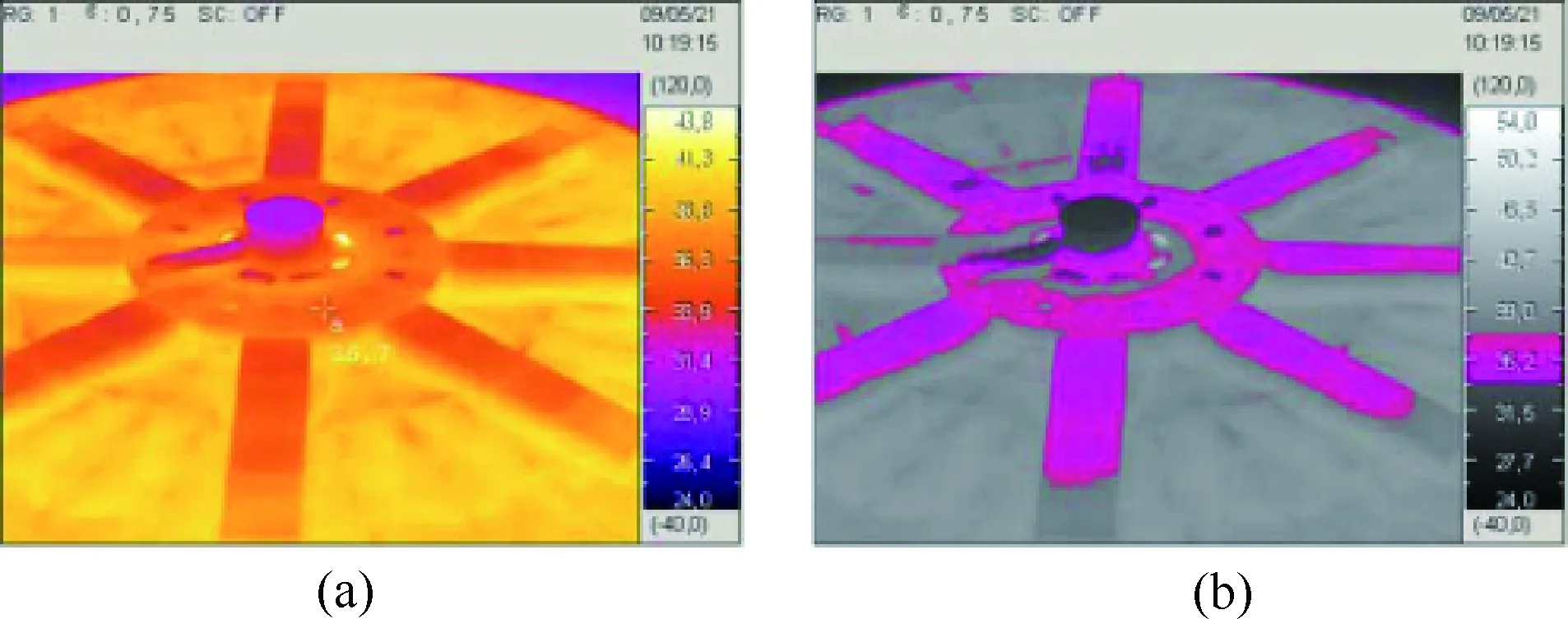
图4 发电机覆盖表面的红外热像和等温线

图4(a)显示了水力发电机表面的热图像，而图4(b)显示了36.2℃附近温度的相关等温线。等温线表面积可以通过多种方式确定。一致的方法在于将满足温度范围标准的像素的数量乘以由每个像素覆盖的基本区域。这个区域涉及瞬时视场(IFOV)，定义了热成像仪的最小可检测目标。热成像仪的最小可检测目标取决于相机的FOV和FPA分辨率。考虑到m×n的FPA分辨率，式2可以被重写为

(12)

式中，I表示所考虑的等温线集合。对于第i个等温线，Ni、hi和Δθi分别是像素的数量、传热系数(W/m2K)和环境温度(K)。

5 发电机轴上的损耗

目前，发电机效率测定标准中经常忽略的损失是发电机传动轴中的传导和对流损失。这部分轴与轴承摩擦产生的热量不是由冷却油提取的，而是通过传动轴传导并作为对流损失释放到环境中。

由于使用传统的接触式温度传感器来测量轴的温度梯度几乎是不可能的，因此轴损耗的能量值被经常性忽略。

红外热像仪的出现为测量此前被忽略的损耗带来了新的可能性，图5显示水力发电机轴的温度梯度超过10℃。

图5 发电机轴的红外热像

虽然轴损失机制遵循式(2)和式(5)所述的理论，但仍然需要采用不同的方法来确定旋转传动轴的努塞尔数：

(13)

式中ω——角速度,rad/s；

D——轴直径，m。

6 案例分析

将本文所提出的发电机效率测定技术应用于江苏省宜兴抽水蓄能电站的额定功率为55.5MVA的单台机组，将通过比较采用本文方法测定出的效率值与制造厂家采用的标准方法获得的效率值来完成对所提技术的可行性验证。

该水电站发电机组的水和空气回路释放了冷却液吸收的热能损失。该发电机组散热系统由六个结构相同风管组成(其中一个风管的截面和风速如图6所示)。使用经过校准的热式温度计和速度计进行温度和风速测量。

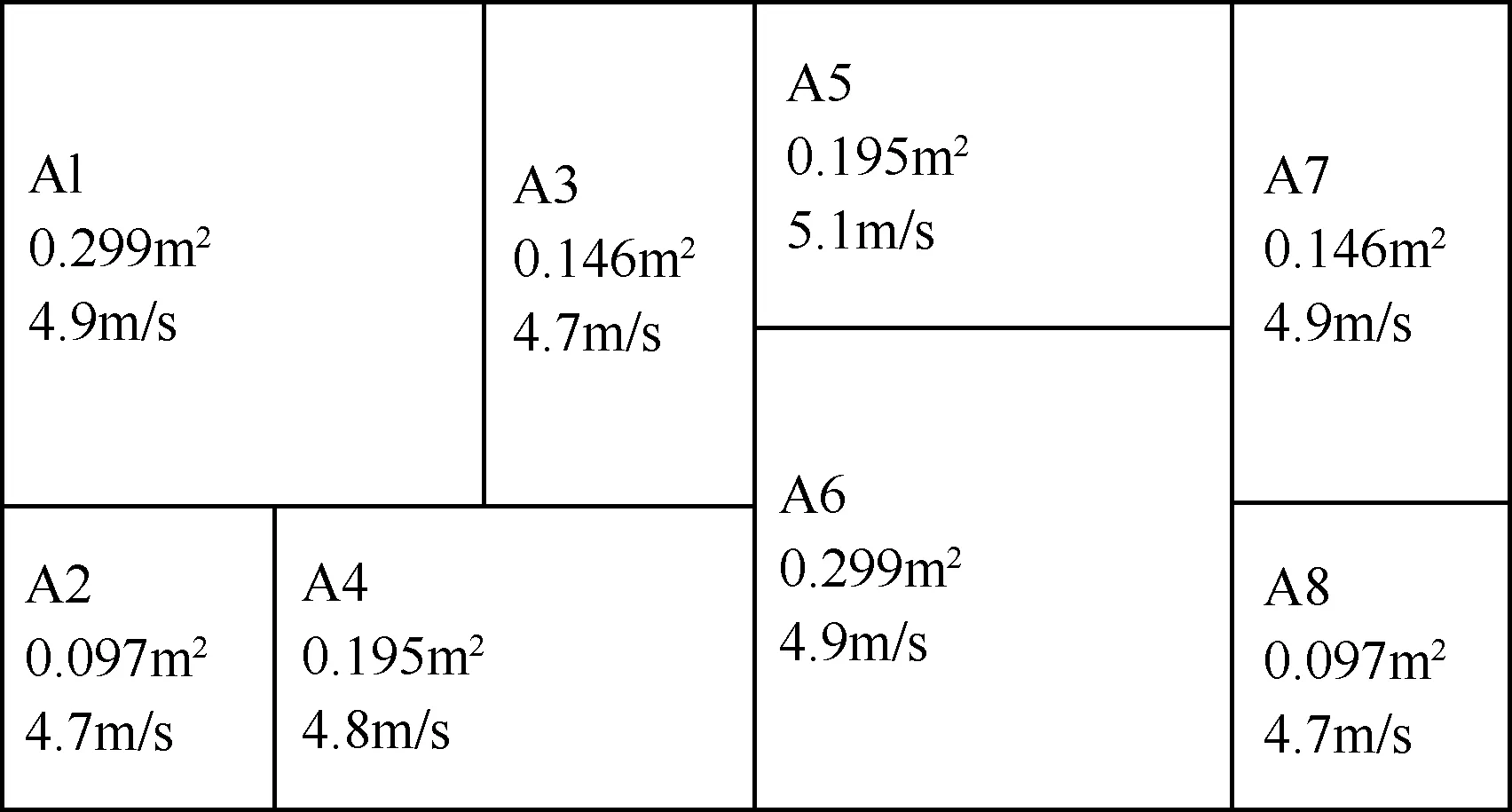
图6 通风管上的风速和面积分布

六个管道的总风量为42.5m3/s; 通风管道输入和输出的平均空气温度分别为49.9℃和66.6℃。因此，由式(2)计算出吸收损失为771.6kW。水回路计算出相同的损失。使用超声波流量计测量的水流量为176.1m3/s。输入和输出温度分别为27.9℃和31.8℃。计算出的冷却液所吸收热量损失为789.7kW。

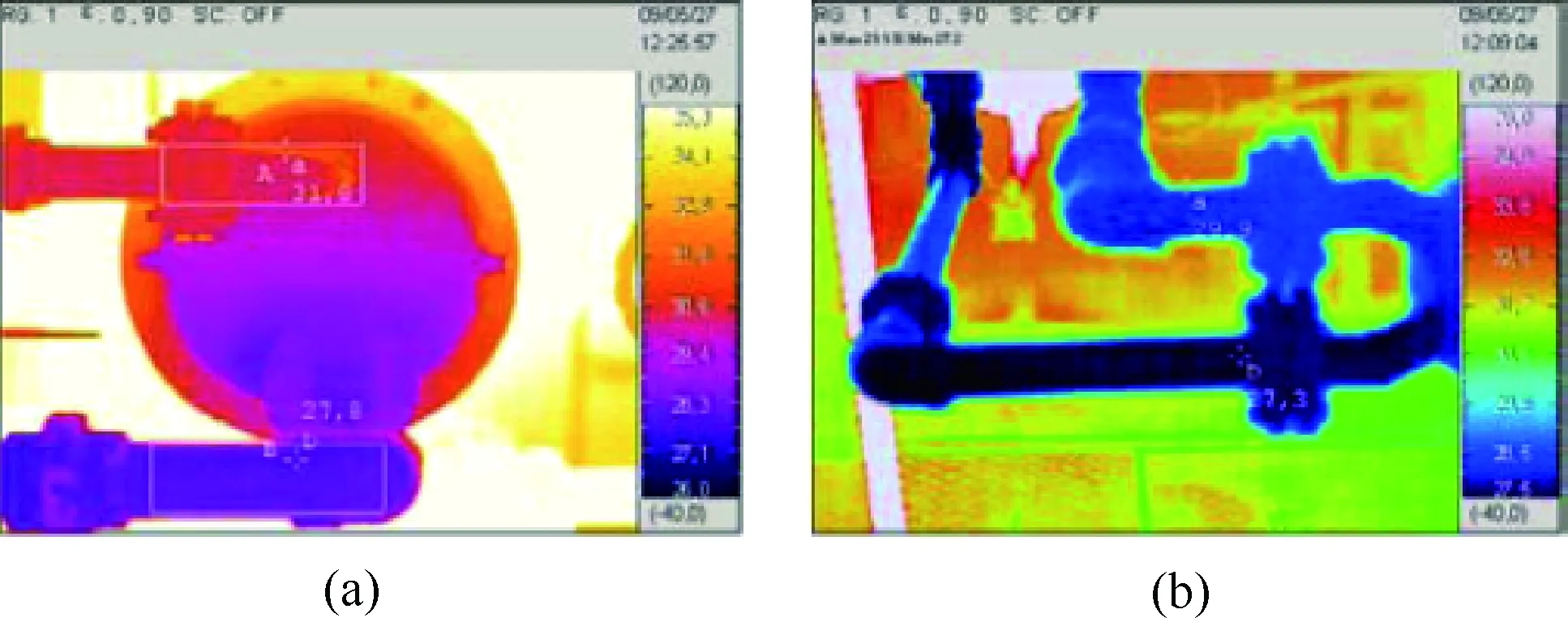
图7 机油冷却轴承的红外热像

如图7所示，通过测量冷却水流量和温差来确定合并轴承和上轴承的水分吸收损失(轴承热损耗测量结果如表3所示)。

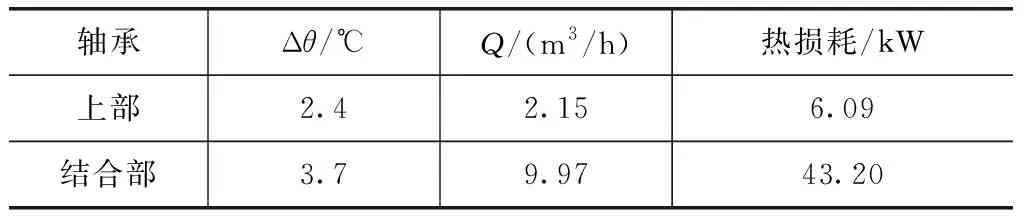
表3 轴承热损耗测量结果

使用红外热成像技术获得水力发电机组外表面的热量损耗。由于FOV的限制，整个区域被分成四个象限,如图8(a)所示。等温线图技术被用来确定温度范围的区域,如图8(b)所示。所得结果列于表4中。

图8 发电机覆盖表面的红外热像和等温线

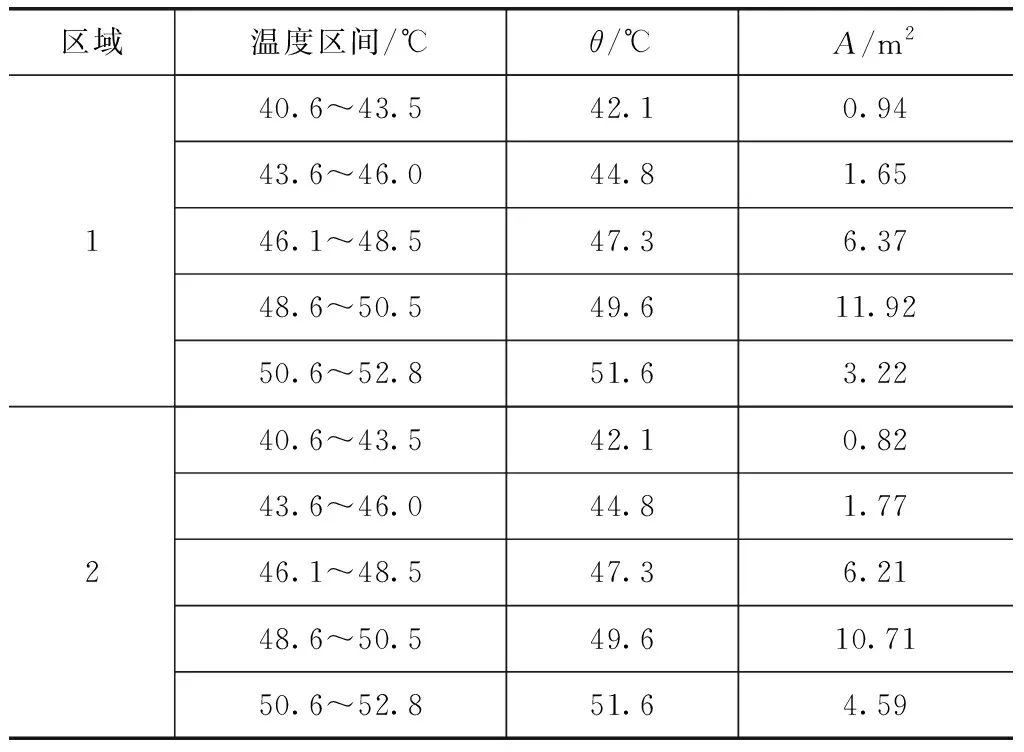
区域温度区间/℃θ/℃A/m2140.6～43.542.10.9443.6～46.044.81.6546.1～48.547.36.3748.6～50.549.611.9250.6～52.851.63.22240.6～43.542.10.8243.6～46.044.81.7746.1～48.547.36.2148.6～50.549.610.7150.6～52.851.64.59

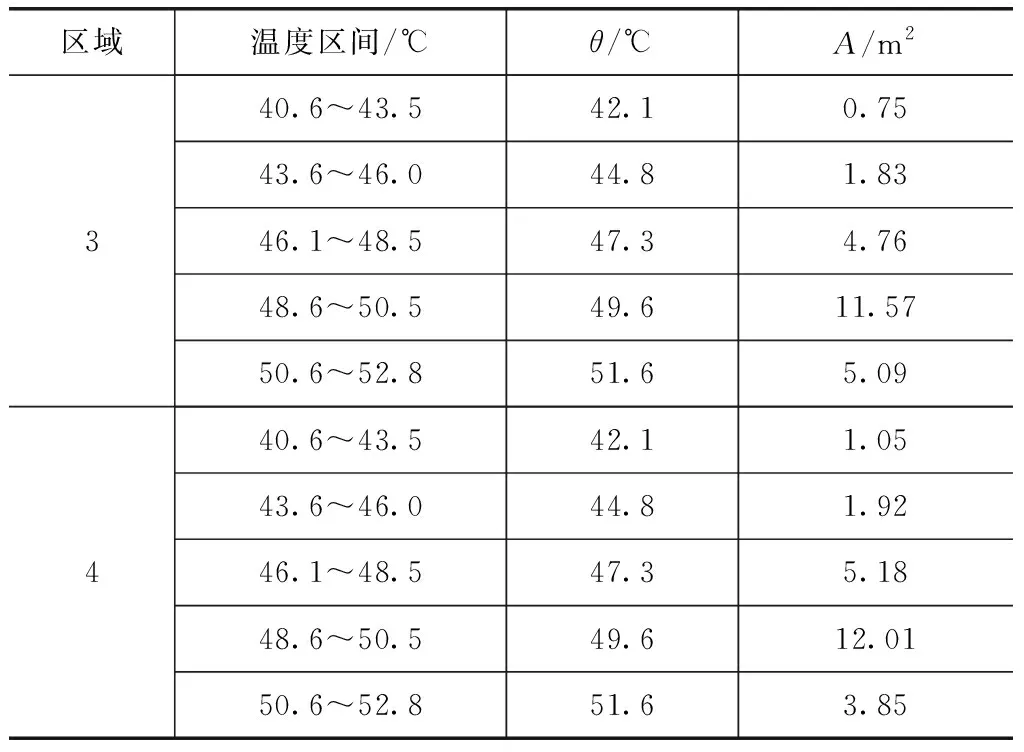
续表

试验环境温度为34.8℃。为了便于比较，传热系数为15W/(m2·K)。测得在发电机表面范围内的泄漏热量损失为20.2kW。采用相同的技术，在励磁机和发电机井中测得热量损失共为24.05kW。

基于水回路和空气回路计算的水力发电机组的总损耗值分别为862.9kW和844.9kW。

表5列出了所计算的效率以及从制造厂家获得的效率值。通过比较，可知所计算出的效率值与制造厂家的标准效率值具有非常好的一致性。

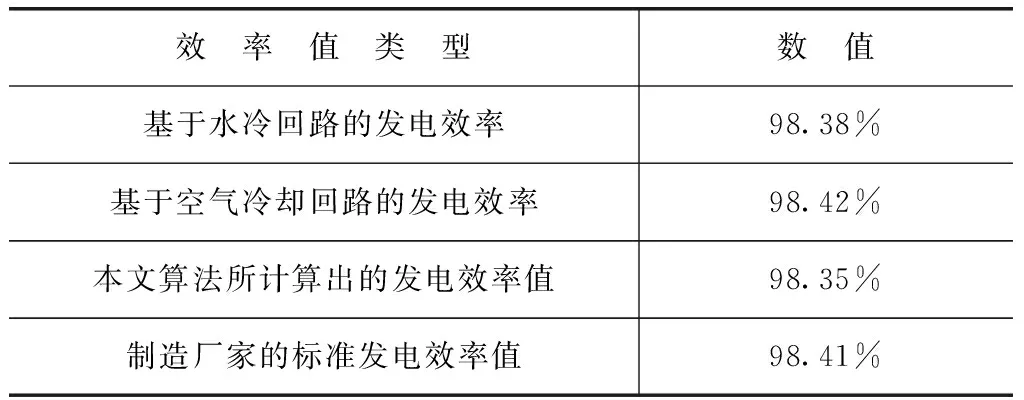
表5 发电效率值对比

7 结 论

本文提出了一种将基于红外热成像的量热法应用于水力同步电机效率测定的方法。该方法利用红外热成像法可快速测得连续范围内水力发电机表面的热损耗，提高了量热法的测量速度、测量精度，同时避免了在水力发电机表面布设大量接触式温度传感器，降低了效率测定的成本。案例分析表明，该方法所测的的效率值与标准值具有较强的一致性，具有推广使用的价值。

[1] 李文金.量热法测量水轮发电机效率[J].水电与新能源,2016(3):36-40.

[2] 王靖,焦海波,李琴,等.高频磁件损耗的量热法测量技术的新方法[J].电力电子技术,2017,51(1):115-117.

[3] 丁韬,成科,钟建.冷却介质对水轮发电机效率值测算的影响[J].四川水力发电,2017,36(6):95-96.

[4] 解乐,刘建国,程寅,等.一种非接触式道面温度测量系统研制[J].电子技术应用,2017,43(6):75-78.

[5] 徐松,孙伟乐,王海峰.轮缘驱动型潮流能发电系统数值分析与试验研究[J].太阳能学报,2017,38(1):194-200.

[6] 倪有源,何强,郎旭初,等.基于场路耦合法计算爪极发电机输出功率和效率[J].合肥工业大学学报(自然科学版),2015,38(3):314-318.

[7] 盛杉,杨明,韩毅.基于量热法的发电机效率试验[J].上海大中型电机,2017(2):4-7.

[8] 王华伟.基于红外热成像的温度场测量关键技术研究[D].西安：中国科学院研究生院(西安光学精密机械研究所),2013.