地铁牵引供电系统直流侧短路故障研究

， ，

(上海工程技术大学 城市轨道交通学院，上海 201620)

0 引言

近年来城市轨道交通发展迅速，合理的轨道线路布局、高效安全的轨道交通运行对于改善市民公共出行条件、缓解高峰时段城市交通压力、优化城市整体发展布局起到重要的促进作用。然而，频发的轨道交通供电系统直流侧供电故障给地铁的安全运营带来了新的挑战，其中最为常见的是牵引供电系统短路故障。为了增强供电系统运行可靠性、提高轨道交通出行安全性，一方面进行线路保护的装置研究[1-2]，使得保护装置灵敏动作切断故障电路，将故障可能产生的危害将至最低，另一方面进行牵引网故障定位的算法研究，利用故障后的线路电气量数据进行故障定位与排查检修，快速恢复轨道交通的正常运行。

各类文献根据整流机组阻抗值随外电路阻抗值变化的特性将整流机组等效为电压源与电阻并联结构，建立线路的等效数学模型，编写程序计算短路电流稳态值，将仿真值与短路试验值作对比验证数学模型的准确性，模型计算结果为线路保护装置动作值的整定提供了理论指导和数据参考[3]。然而，使用分段线性的数学模型代替非线性的整流机组模型，在计算近端短路故障时不能准确反映故障时非线性的暂态电气参数变化过程。其次，随着保护算法和保护装置的发展，保护机构能够迅速动作切断电路，使故障电流无法到达稳态值，基于故障电流稳态值的故障定位算法因缺乏充足的数据而直接失效[4]。最后，随着现代仿真软件的发展，建立轨道交通供电系统模型，计算故障电流暂态值，运用极少的暂态电流数据代替稳态电流数据进行故障定位成为新的研究方向。

城市轨道交通牵引供电系统的交直流变换过程和集肤效应作用下牵引网的阻抗值变化对牵引网短路故障暂态电流的影响是研究直流侧短路故障暂态过程的重点。根据实际系统设备仪器与牵引网线路参数，在Matlab/Simulink环境下对轨道交通的直流牵引供电系统建立模型，针对不同故障距离进行仿真，得到不同距离短路故障暂态过程中电流的暂态变化数值，为基于暂态电流值的故障定位方法提供数据参考。

1 城市轨道交通牵引供电系统

1.1 牵引供电系统结构

典型的城市轨道交通供电系统一般包括高压供电源系统(城市电网)、牵引供电系统与动力照明供电系统三部分。高压供电源系统采用不同的供电方式经交流母线为牵引供电系统输送高压(35 kV)或中压(10 kV)三相交流电，牵引供电系统通过牵引变电所将三相交流电转变成适用于轨道车辆的低压直流电(750 V或1 500 V)，经馈电线将直流电输送至牵引网(接触网或第三轨)，轨道车辆通过受流器(受电弓或受电靴)与接触网的直接接触获得电能，并由走行轨和回流线返回至负极[5]。以双边供电方式为例，城市轨道交通牵引供电系统结构如图1所示。

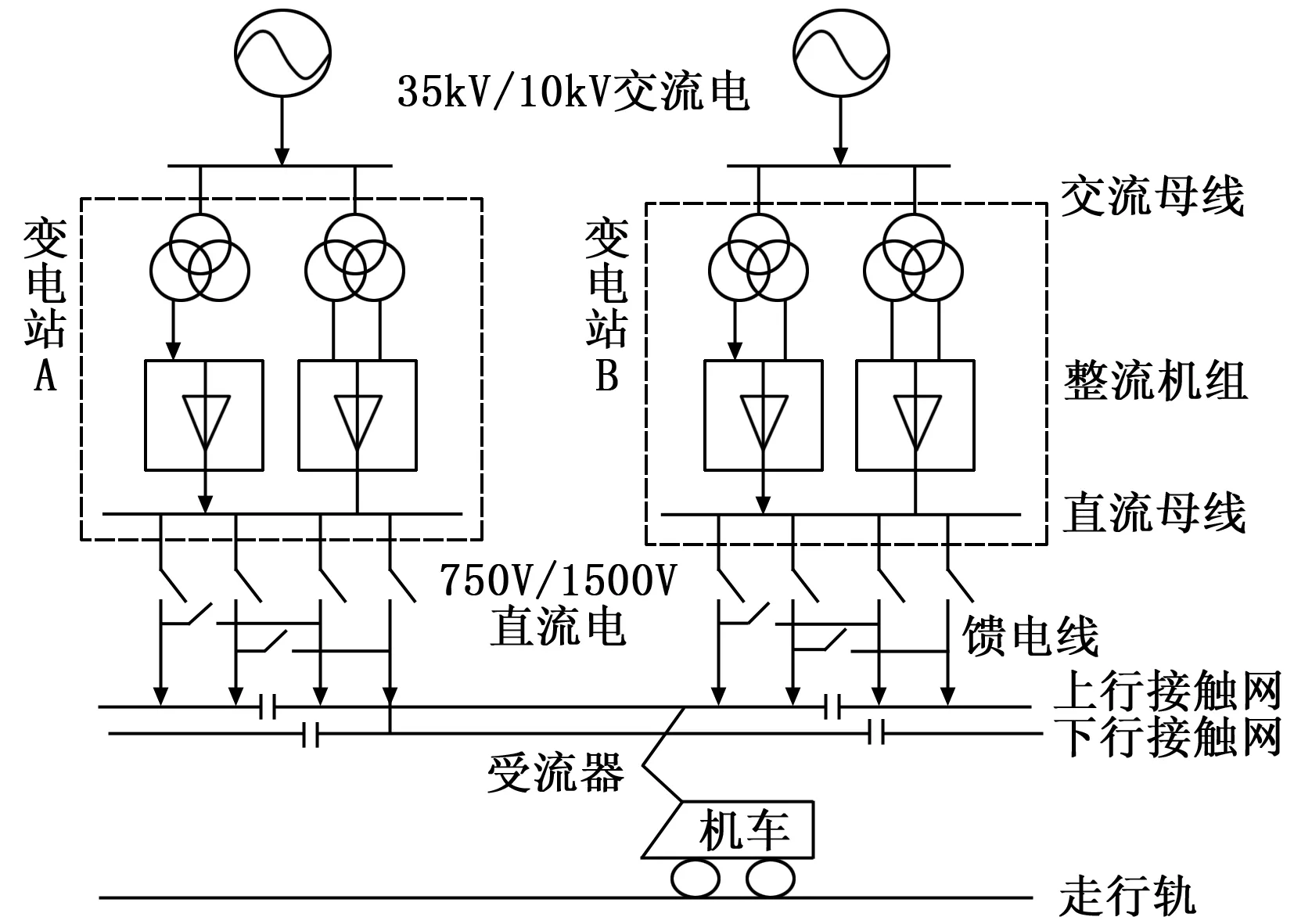
图1 城市轨道交通直流牵引供电系统示意图

1.2 牵引供电短路故障

城市轨道交通牵引供电系统短路故障主要包括牵引网短路故障、直流母线短路故障和整流机组内部短路故障等。其中，牵引网长期处于与受电弓的动态摩擦的工作状态下，牵引网装置直接暴露于大气环境下，工作环境受天气状态与环境污染等因素的影响，易发生短路故障。一旦发生短路故障，线路保护装置动作导致线路供电中断，影响轨道交通正常运营。牵引网短路故障根据故障原因不同，可分为金属性短路故障、非金属性短路故障及特殊情况下的异常运行状态，根据故障点距变电站位置不同可分为近端短路故障和远端短路故障。

2 牵引供电系统模型

2.1 整流机组模型

牵引变电站作为轨道交通牵引供电系统中进行交直流变换的关键环节，其主要工作设备是由整流变压器与整流器组组成的整流机组[6]。整流机组作为供电系统中的非线性负载，是产生交流侧谐波电流，造成电力系统电流波形畸变的根本原因之一，对轨道车辆的驱动系统产生干扰，影响轨道交通系统用电设备和信号系统的正常运行，甚至造成输电线路故障。通常，牵引变电站将整流机组并联以减小整流元件的导通角、增加整流装置脉动数的方式减少交流电源端的低次谐波，从而将注入城市高压电网的谐波含量控制在许可范围内，降低对城市电网系统的影响。目前，牵引变电站通常将两台相位相差±7.5°的12脉波整流机组并联，组成24脉波整流机组系统。

首先，将两个三相桥式整流电路和整流变压器构成12脉波整流电路。其中，整流变压器二次绕组分别采用星形和三角形接法，构成幅值大小相等、相位相差30°的两组输出电压，输出电压在每个交流电源周期中脉动12次，将这两组电压接入相互并联的三相桥式整流电路中，即构成12脉波整流电路。其次，使用移相变压器将两路12脉波整流电路分别移相±7.5°，将移相后的12脉波整流电路并联构成24脉波整流电路。

根据上述原理，在Matlab/Simulink环境下建立24脉波整流电路仿真模型如图2，根据牵引变电站实际整流机组数据设置模型参数。模型中采用相位相差 ±7.5°的两个三相电源代替移相变压器，使12脉波整流变压器的原边分别移相+7.5°和-7.5°。

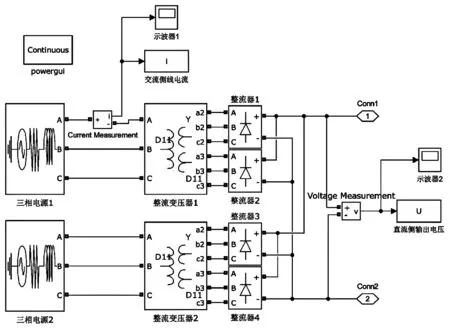
图2 二十四脉波整流电路模型

24脉波整流电路输出电压波形如图3，波形在一个周期(0.02 s)内脉动24次，波动间隔为15°，仿真结果证明了该模型的正确性。

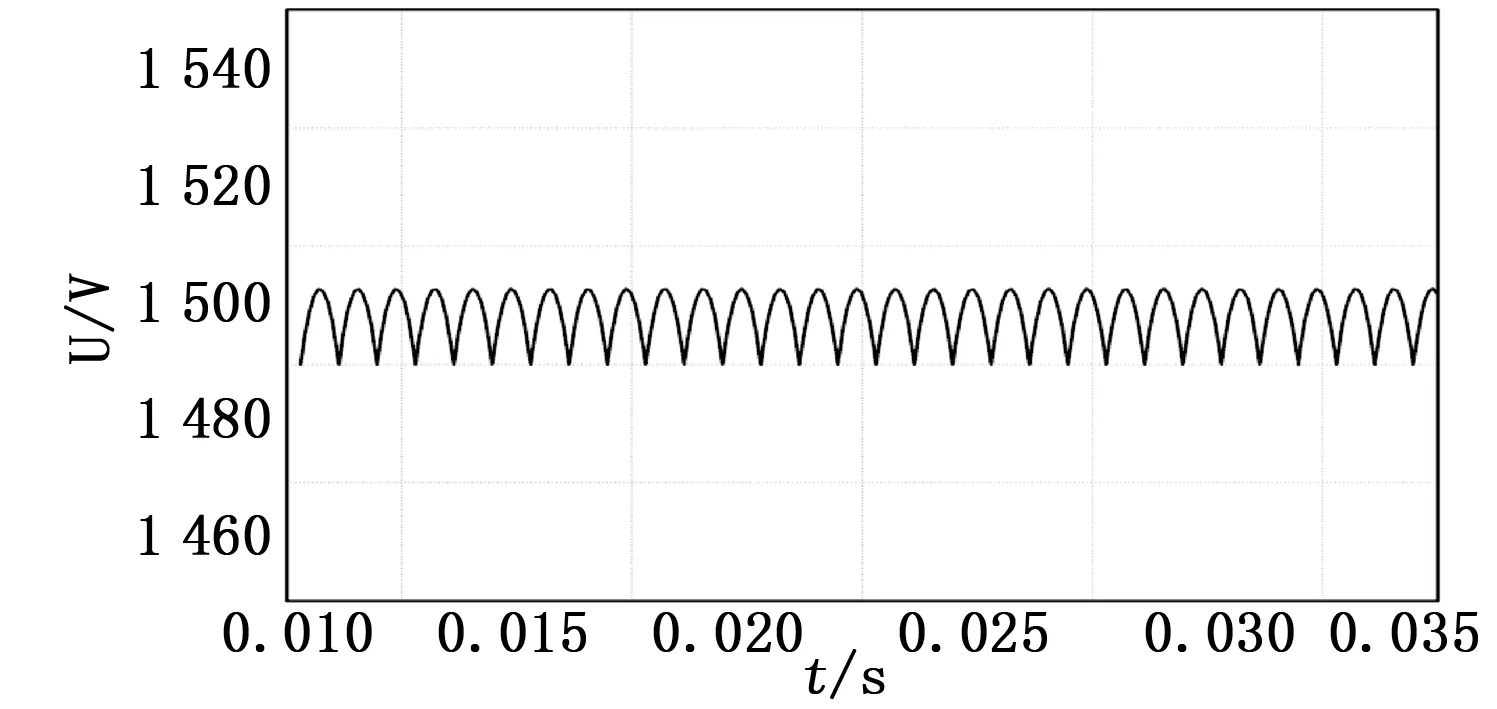
图3 二十四脉波整流电路输出电压波形

2.2 接触网—轨道阻抗模型

2.2.1 接触网—轨道稳态阻抗

当供电系统正常工作时，假设流经牵引网中直流电流均匀分布，则单位长度导体直流电阻与直流内电感的计算公式为：

(1)

(2)

式中，σ为通电导体电导率，S为导体的横截面积，μ为相对磁导率，μ0为真空磁导率。

2.2.2 接触网—轨道暂态内阻抗

接触网与轨道的暂态内阻抗包括故障暂态下接触网与轨道的电阻与电感值。当轨道交通正常运行时，接触网与轨道的阻抗值采用式(1)、(2)计算。但在短路故障发生后的暂态过程中，电流频率变化，由于集肤效应的作用，电流将汇聚到集通电导体表面，使得通电导体的有效截面积减小，导体电阻值增大。此时穿过通电导体有效截面的磁通量减小，内电感就相应减小。对于横截面不规则的钢轨而言，其集肤效应的作用尤其明显。通常采用等周长的圆柱截面代替不规则截面[7-8]计算通电导体的电阻与电感值,其单位长度的内阻抗的表达式为：

(3)

式中,ω为电流角频率，Ra为通电导体的等效半径，I0和I1为一阶零类贝塞尔函数与其导数，其表达式为：

(4)

由于此公式计算过程较为复杂，通常工程上会分别给出高频、低频下的导体内阻抗值的近似表达式：

(5)

(6)

不同导体电磁参数如表1所示，其中临界频率即为判断导体处于高频或者低频的临界参数。

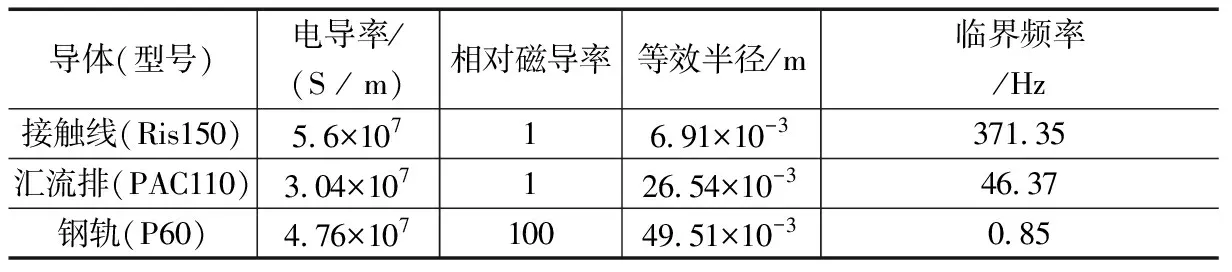
表1 直流牵引网导体参数导体

由式(4)(5)可知，导体阻抗主要取决于电流角频率ω，因此当发生短路时，使用传统的直流或50 Hz时阻抗值会产生较大误差。根据短路故障的现场数据分析[9]，超过半数的暂态电流频率在10～25 Hz之间，现采用10 Hz作为暂态过程中的电流频率计算接触网与钢轨的阻抗值。根据通电导体的临界频率不同，分别使用式(6)计算接触网与汇流排暂态内阻抗值，使用式(5)计算钢轨的暂态内阻抗值。将汇流排与接触线并联，记为接触网，将上下行钢轨并联，记为钢轨网，单位长度钢轨网与接触网的内阻抗值计算结果如表2。

表2 单位长度接触网、钢轨网暂态阻抗值

2.2.3 接触网—轨道外电感

牵引网的阻抗模型既包括暂态内阻抗，还包括外电感值。接触网与轨道的外电感是指外部空间磁场与导体内电流交链形成的电感。对于任一轨道或接触网中的电流，与其交链的磁场既有自身电流产生的磁场，也有其它轨道或接触网中电流产生的磁场。因此，接触网和轨道的外电感包括外自感和互感。对于不同的牵引网结构，其计算方式不同，现采用架空接触网与双轨道结构计算其外电感值。

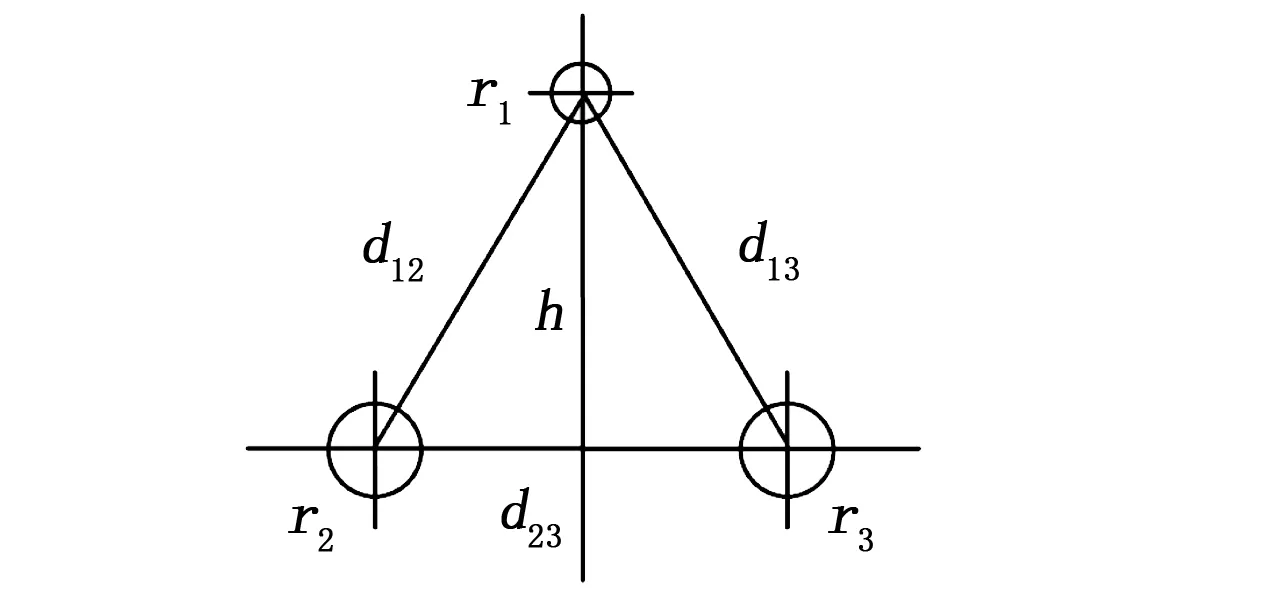
图5 接触网-轨道结构外电感计算示意图

接触网-轨道结构外电感计算示意图如图5。其中，r1、r2、r3分别为接触网和钢轨等效半径，d12、d13、d23为通电导体之间相互距离。推导过程[9]不再复述，各导体的外电感表达式为：

(7)

(8)

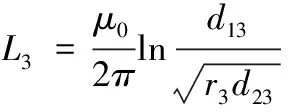
(9)

根据钢轨网与接触网材料，经计算得接触网外电感为0.9 mH / km，钢轨网外电感为1.1 mH /km。

综上，对接触网和钢轨网的内外电阻、内外电感求和，得到单位长度接触网和钢轨网的阻抗参数如表2。

表2 单位长度接触网、钢轨网阻抗值

3 模型仿真分析

3.1 近端短路故障仿真分析

当牵引变电所近端发生短路故障时，故障瞬间会产生很大的暂态冲击电流，电流变化过程受整流器换阀过程和整流机组参数的影响，因此仿真分析时必须考虑详细的交直流变换模型，即24脉波整流器模型。

在Matlab/Simulink环境下建立城市轨道交通双边供电下的供电系统模型[10]。通过设置牵引网阻抗值确定线路长度与故障点位置，设两变电站相距2 km，在变电站A近端50 m、100 m、200 m、500 m处设置短路故障，过渡电阻0.00 1 Ω，程序运行0.3 s后发生短路，距离仿真结果如图6所示。

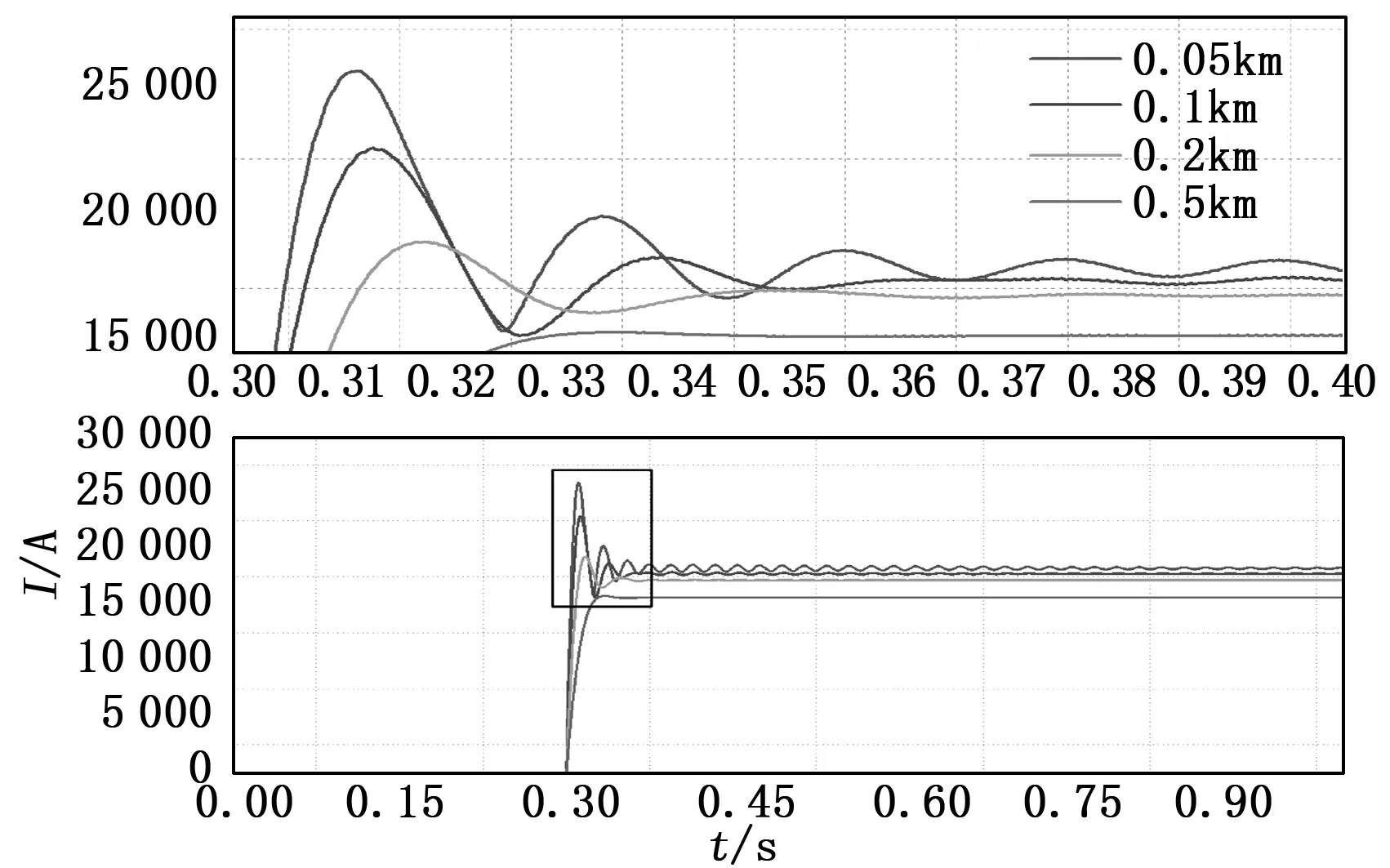
图6 近端短路电流

如图6，短路故障发生瞬间电流急剧上升，呈指数增长形势，在短时间内到达稳定值。电流值达到稳态值前发生振荡波动，故障地点与牵引变电站距离越近，其故障电流峰值波动越剧烈。该波动特征充分反映了交直流变换环节对近端短路故障电流值瞬态值的影响，根据整流机组外特性所建立的线路等效数学模型并不能准确描述这一瞬态变化。

3.2 远端短路故障仿真分析

在牵引变电站A远端1 500 m、1 800 m和1 900 m处设置短路故障，其他设置条件与近端短路故障相同，远端短路故障仿真结果如图7。

如图7，远方短路故障时，电流瞬时剧烈上升，其上升趋势与近端短路相似，但暂态电流的振荡波动现象消失，表明交直流变换环节对暂态电流的影响可以忽略不计。不同距离的电流上升率相同但峰值不同，说明此时对短路电流暂态值起关键作用的是牵引网和钢轨网系统的阻抗值，距离越远阻抗值越大，电流增量越小。

4 结论

本文在介绍城市轨道交通牵引供电系统结构、总结常见牵

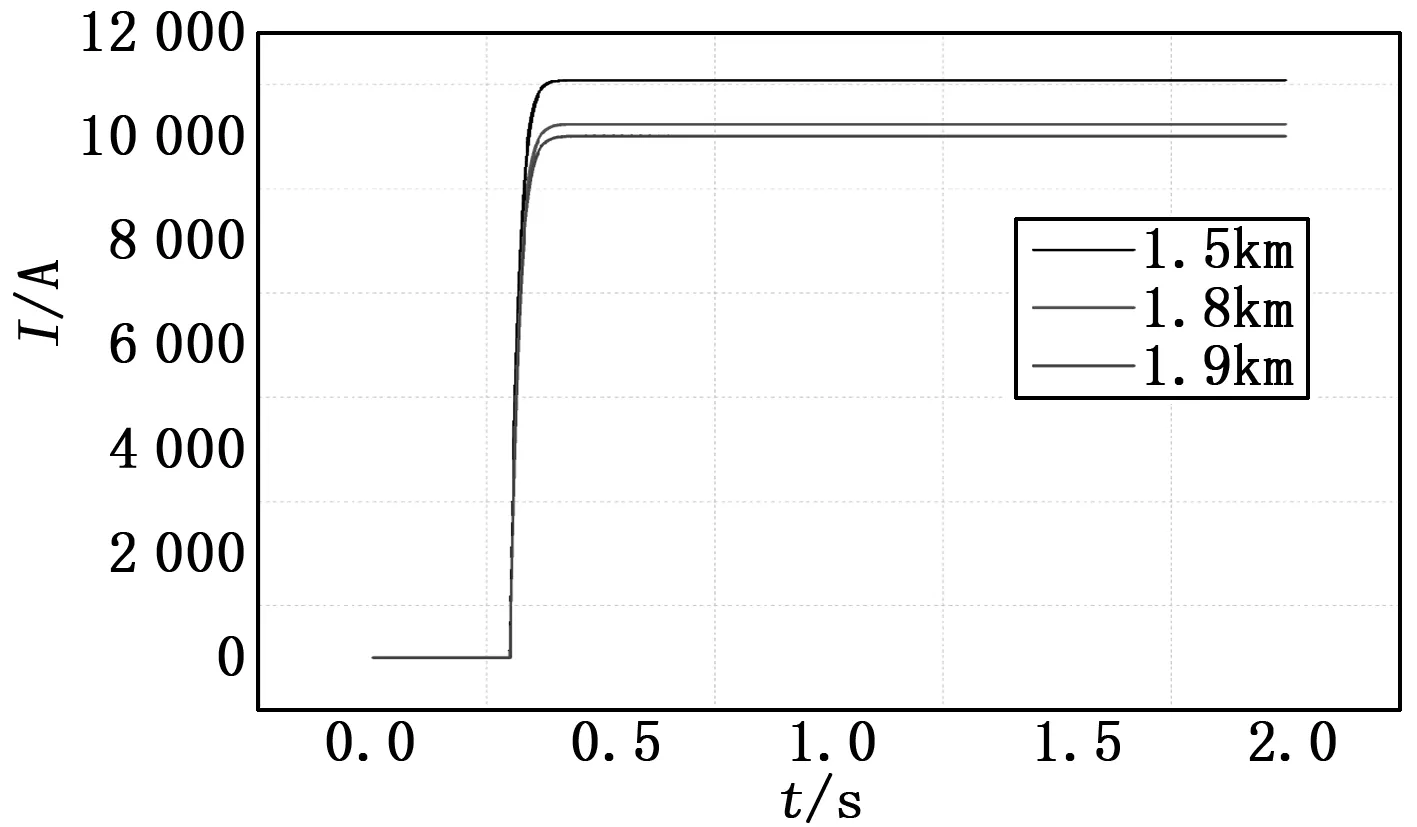
图7 远端短路电流

引供电系统短路故障类型和分析计算集肤效应作用下接触网与钢轨阻抗值的基础上，建立了城市轨道交通牵引供电系统牵引网短路故障仿真模型，利用仿真研究了短路故障暂态过程中线路电流的暂态变化规律。

1)当牵引网发生短路故障，电流值呈指数形式增长，且在极短时间内趋于稳定；

2)由于非线性的整流机组的影响，近端短路会产生极大的暂态冲击电流，该电流呈现振荡收敛趋势，使用整流机组等效数学模型无法准确描述该现象。

3)随着短路点距离增加，整流机组对短路瞬态值的影响减小，短路电流增量减小，稳态电流值下降，此时影响线路电流的主要因素是牵引网阻抗值。

参考文献:

[1]单保强, 张红江, 薛思才, 等. 城轨车辆受流器熔断器的选型研究[J]. 铁道机车车辆, 2014, 34(5): 51-54.

[2]曹晓明, 庄 军. 高速断路器试验台的研制[J]. 铁道车辆, 2015, 53(9): 39-40, 10.

[3]肖涛谷. 地铁直流供电系统模型及直流短路分析[D]. 广州：华南理工大学, 2012.

[4]宋国兵, 蔡新雷, 高淑萍, 等. 高压直流输电线路故障定位研究综述[J]. 继电器, 2012, 40(5): 133-137, 147.

[5]王俭朴. 城市轨道交通电力牵引与控制[M]. 北京: 国防工业出版社, 2011.

[6]谢 方. 城市轨道交通直流供电整流机组研究[D]. 成都：西南交通大学, 2009.

[7]吴命利, 范 瑜. 圆导线内阻抗的数值计算[J]. 电工技术学报, 2004, 19(3): 52-58.

[8]鲁小兵, 周文卫, 王元贵. 基于集肤效应的地铁短路时间常数研究[J]. 电气化铁道, 2012, 23(4): 41-43, 47.

[9]张 勋. DC1500V牵引供电系统故障测距研究[D]. 成都: 西南交通大学, 2014.

[10]李 献, 骆志伟, 于晋臣. MATLAB/Simulink系统仿真[M]. 北京: 清华大学出版社, 2016.