梯形区间二型模糊群决策发生算法及其综合比较法

邵小十,王铁旦,彭定洪

(昆明理工大学 质量发展研究院,昆明 650093)

1 引 言

信息爆炸和信息碎片化使得人类思维和客观现实的复杂性急剧增加,进而增加了实际决策的复杂性.这种情况下,个体信息及知识储量的局限性尤为凸显,难以做到决策科学化,而群体决策则可以以集体智慧突破个体决策的局限性,得以广泛运用.尤其在决策支持信息较少的前瞻性决策过程中,需要借助群体的不同专业背景、不同阅历经验,综合考量每一个人提出的潜在可能情况,进而得到可信度与可靠度更高、风险更小的决策结果.因此,群体决策准则值往往带有模糊不确定性,难以给出具体数值,而采用模糊数方法评判决策对象能够得到较好的决策效果.近年来,随着隶属函数概念的拓展和延伸,相较一型模糊数,二型模糊的隶属函数能够更好地刻画数据的模糊不确定性,得到更加精确和健壮的结果[1].其中,针对高度不确定的现实环境,梯形区间二型模糊(IT2 TF,Interval Type-2 Trapezoidal Fuzzy)的隶属函数更加符合实际决策情况,因此能够得到更加科学、更加稳健的结果.

到目前为止,利用区间二型模糊数的隶属函数解决多准则决策问题的研究很少.Chen[2]提出根据隶属函数的高度和广度排序一般模糊数并以此进行决策,但该方法仅适用于对一型模糊隶属函数的研究上.Chen[3]提出利用二型模糊上下隶属函数边界值的均值构造得分函数,再结合TOPSIS方法进行最优决策.相较前一种方法,后一种方法因引入了二型模糊使其在处理多准则决策问题时更加灵活、有效[4],故Chen[5]再次将此方法进行改进用以解决多准则群体决策问题.Chen[6]引入截集理论提出新的隶属函数面积求解法用以解决多准则决策问题.Chen[7]提出以隶属函数到纵轴的距离作为距离测度的QUALIFLEX决策方法.Heidarzade[8]提出以聚合二型模糊足迹区域面积作为距离测度的供应商选择方法.Kahraman[9]根据上下隶属函数的最大值、最小值和隶属度最高值六个点构造得分函数并结合AHP理论进行排序.Keshavarz[10]提出一种改进的质心间距离算法结合VIKOR方法解决多准则群体决策机器人选择问题.Qin[11]将二型模糊的边界点与多种聚合算子相结合,得到混合排序值以解决多准则群体决策问题.

纵观模糊决策的相关文献,其核心问题就是解决对模糊数的排序问题,排序的结果对应着决策方案的优劣.其中,隶属函数对模糊数起着决定性的意义[12].然而,现行的决策方法都是基于对隶属函数的隐性运用,很少有针对隶属函数进行研究的决策方法.利用模糊数的隶属函数表达决策中模糊不确定性信息的方法多停留在对隶属函数整体的比较上,或研究整体的重心、或研究整体的面积(包括对二型模糊足迹区域的研究,或对上隶属函数与x轴所辖区域的研究).无论哪种方法都会混合或模糊了隶属函数所表示的隶属程度与其模糊不确定性信息之间的关系,导致无法充分利用隶属函数的高隶属信息和模糊不确定性信息,难以解决高度不确定环境和群体决策需求的冲突,使得决策结果难以符合现实要求,直接影响了决策结果的科学性和有效性,失去了引入模糊数的核心优势.因此,只有从隶属函数角度入手,深刻分析隶属函数的内涵和原理,才能充分利用其包含的数据,完成对模糊不确定信息的处理.

关于二型模糊数隶属函数,Mendel J.M.等针对其内涵和原理进行了一系列研究,文献[13]利用区间二型模糊隶属函数与加权平均聚合算子的结合进行语言的编码与解码,文献[14]中讨论了质心降型二型模糊数与隶属函数之间的关系,文献[12]中给出了隶属函数相关定义和符号的澄清和补充说明.

基于上述文献的研究,本文重点研究隶属函数的内涵和原理,并结合聚合算子[15]、截集理论[6]、几何原理[16]等方法,以充分挖掘和利用隶属函数中的相关信息,构建群决策发生算法,提出梯形区间二型模糊隶属函数综合比较法,发挥出梯形区间二型模糊在解决多准则群体决策问题中的优势.最后通过实例分析验证了本文方法的科学性和有效性.

2 基础理论

2.1 梯形区间二型模糊

自1965年Zadeh L.A.提出模糊理论[17]以来,数学领域的研究范围由精确现象领域扩大到模糊现象领域[18],尤其是模糊理论在包含人类复杂判断的模糊不确定环境下的相关决策问题中的应用,提高了客观数据与人类实际决策活动间的契合度,更加全面真实的反映出人类群体决策活动中的模糊不确定性,进而提高了群体决策研究结果的精确度.其中,梯形区间二型模糊既体现出高隶属程度的范围又记录下模糊不确定的隶属情况,是模糊数理论中反映人类活动模糊不确定性能力最强的一种数据形式,因此本文基于梯形区间二型模糊对多准则群决策方法进行研究.

现对梯形区间二型模糊的核心内容和相关定义进行简要说明,如定义1,2,3所示.

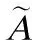
∀u∈Jx⊆[0,1]}

(1)

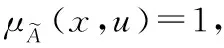
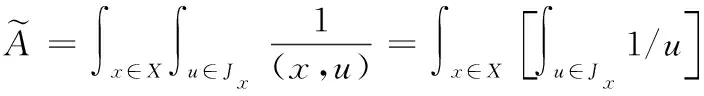
(2)

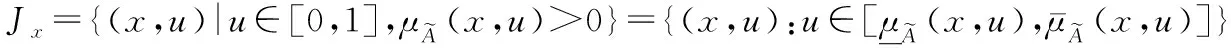
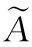
(3)

图1 梯形区间二型模糊数Fig.1 Interval Type-2 trapezoidal fuzzy Number

定义3.[2]梯形区间二型模糊(IT2 TFS,interval type-2 trapezoidal fuzzy set)参数表达式为

(4)

在梯形区间二型模糊数中,根据其参数形式可得到各顶点坐标,进而可转换成隶属函数的线性表达式.因此,IT2 TFS隶属函数的参数形式与函数形式之间的转换满足不确定性表达准则的同等表达性,本文中为便于计算,采用其参数形式.

2.2 梯形重心公式

重心(Center of gravity,COG)是最具代表性的图形特性之一,因此常作为图形相似性的关键指标.传统的方法皆应用重心处理整体隶属函数,既没有充分发挥出重心在区别模糊等级中所具有的代表性,又存在对隶属函数中模糊不确定性的处理缺乏针对性而粗糙失准的问题.为此,本文针对高隶属区域采用重心法进行处理,既充分发挥了重心的代表性含义,又能规避粗糙失准的问题.

鉴于本文应用重心比较模糊数的方法与传统方法不同,故在此加以简要说明.依据文献[16]所述重心求解原理,本文推算出基于二维向量和线性方程的一般梯形的重心求解方法.

假设一般梯形ABCD,其四个顶点坐标为A(a,h1)、B(b,h2)、C(c,h2)、D(a,h1),且a≤b≤c≤d、h1≤h2,则根据梯形重心定义可得公式(5).

(5)

解公式(5)方程可得:

(6)

3 梯形区间二型模糊多准则群决策方法

3.1 群决策发生算法

在多准则群体决策问题中,能否均衡有效的处理好个体之间的差异及其对群体结果的影响问题,是有效解决群决策问题的关键.受文献[19]的启发,根据文献对梯形区间二型模糊隶属函数的分析,进一步考虑群体决策对最大隶属程度的影响,构建出群体决策的梯形区间二型模糊发生算法,具体算法如下:

输入:K个决策者的评价值P={pk|k=1,2,…,K},其中

输出:群体决策评价值

Q=((aU,bU,cU,dU,hU),(aL,bL,cL,dL,hL)).

Step1.将首次输入的评价值作为初始值,即

Step2.根据输入的新评价值pk,生成新隶属度区间上界hU=max(hU(AU),hU(pk)),其中hU(AU)为聚合前AU的hU值、hU(pk)为新评价值pk的hU值;

Step3.根据输入的新评价值,生成新隶属度区间边界值

(7)

(8)

其中hL(Pi)为评价值pk的hL值;

Step4.重复Step2和Step3,直至完成K个评价值的输入;

Step5.得到群体决策评价值

Q=((aU,bU,cU,dU,hU),(aL,bL,cL,dL,hL)).

3.2 综合比较法

根据定义2可知,区间二型模糊数是由在X上的若干任意点的不确定性足迹形成的.通过若干任意点的足迹记录了该模糊数的主要隶属值及其模糊不确定的情况.因此,在对IT2 TFs进行比较时应根据隶属度的不同情况分别进行比较,以最大限度保留模糊及不确定性信息,保证比较结果的精确度,降低决策的风险.

Step1.隶属度的主值区域表示该模糊数的主要对应区域值,即该模糊数隶属程度最高的值域,此值域为该模糊数表示的核心数值情况,因此需要优先处理.

(9)

如图2所示,根据公式(6)可得公式(9).

其中,xig为主值区域核心数值的指标,yig为主值区域隶属程度的指标,将两者相乘,得到Sc0i:

Sc0i=xig·yig

(10)

Scoi作为主值区域的初始计分值,是对模糊数隶属度最高的区域进行比较的依据.根据不同决策环境对数据精度与计算复杂度的不同要求,选择不同的区分度单位值.一般情况下,基于均衡考虑取0.5单位值为宜.

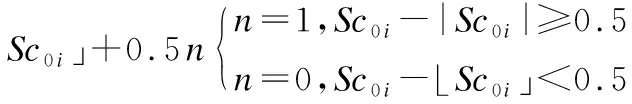
(11)

经过数据精度处理后,对于梯形区间二型模糊数Ai,称Sci为该模糊数对主隶属值的主计分.

Step2.根据文献[6],对于表示模糊不确定性的部分,本文采取α截集方法进行分析比较.

(12)

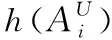
图2 α截集的梯形区间二型模糊数Fig.2 Interval Type-2 trapezoidal fuzzy α-Cut Set

(13)

(14)

计算上隶属函数的左右风险系数,其中α代表决策者的风险态度.当α=0.5时对风险持中立态度;当0.5<α≤1时对风险持偏好态度;当0≤α<0.5时对风险持规避态度.

(15)

(16)

(17)

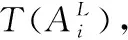
(18)

(19)

(20)

计算下隶属函数的左右风险系数.同上隶属函数相同,当α=0.5时对风险持中立态度;当0.5<α≤1时对风险持偏好态度;当0≤α<0.5时对风险持规避态度.

(21)

(22)

(23)

根据公式(11)、(17)、(23)求得的主计分值及其离散计分值,得到梯形区间二型模糊数Ai的综合比较计分值.

(24)

3.3 梯形区间二型模糊多准则群决策方法

综上所述,基于梯形区间二型模糊群决策值发生算法和综合比较法,对梯形区间二型模糊多准则群体决策问题的完整求解步骤如下.

Step2.按照公式(9)求解群决策值Qij的主值区域核心数值的指标xig和主值区域隶属程度的指标yig.按照公式(10)、(11)计算,得到Qij的主计分值Sc1ij;

Step5.按公式(24)计算出综合比较计分值Scij;

Step6.按照方案m个属性的综合比较计分值Scij的WAA算子值的大小,比较出最优方案.

(25)

4 实例分析

4.1 实例详解

本文引用文献[20]的实例数据进行数据验证和结果分析.该案例为台湾长庚纪念医院神经科的医疗决策问题.

表1 群决策矩阵Table 1 Group decision-making matrix

一个5人的医疗团队结合病人的病史病历和现在身体状况对提出的3种治疗方案进行讨论并决策:类固醇疗法z1、血浆取出法z2和白蛋白免疫疗法z3.从存活率c1、副作用的严重性c2、并发症的严重性c3和治愈率c4等4个方面对治疗方案进行评价,每个专家给出的决策矩阵见附录表12.

表2 各方案的主计分值Table 2 Main points in every scheme

将专家对每种治疗方案不同角度的评价值输入3.1节所述群决策发生算法,得到群决策评价值,所得结果如表1所示.

按照公式(9)、(10)、(11)计算各方案的主计分值,所得结果如表2所示.

在计算上、下隶属函数的离散计分值时,针对不同的风险态度,会有不同的结果.为方便计算以及成果展示,本文对风险态度指标α分别取0、0.5和1,以计算在采取规避风险、中立态度和追求风险态度时的不同结果.

表3 α=0时上隶属函数的离散计分值Table 3 Value of discrete points of upper membership function At α=0

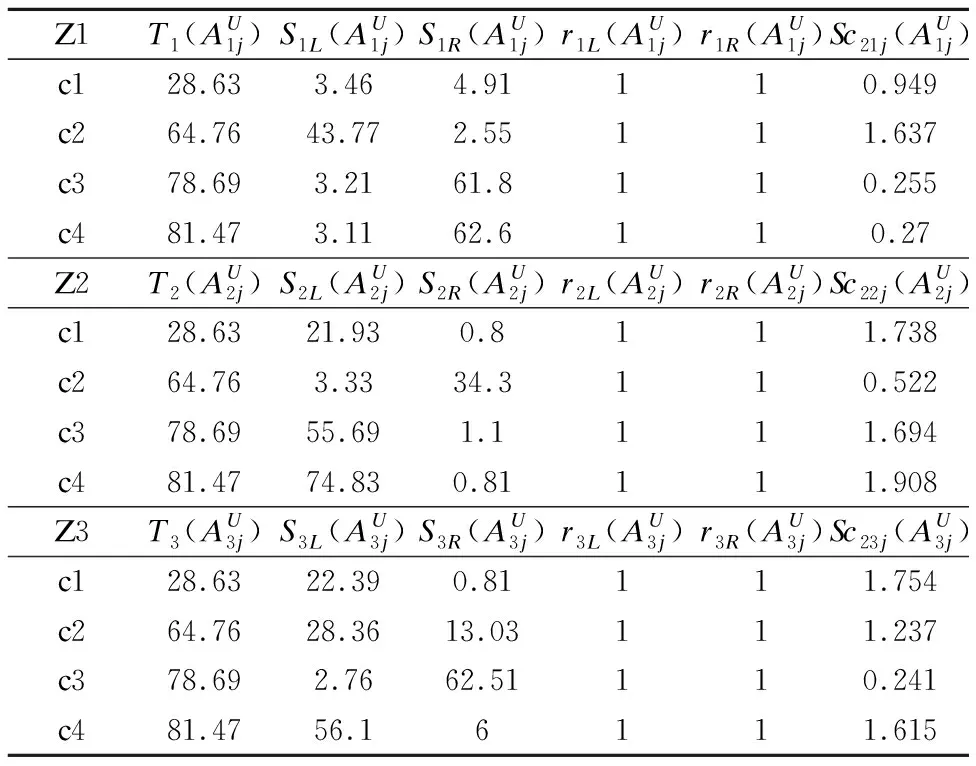
表4 α=0.5时上隶属函数的离散计分值Table 4 Value of discrete points of upper membership function At α=0.5

表5 α=1时上隶属函数的离散计分值Table 5 Value of discrete points of upper membership function At α=1

表6 α=0时下隶属函数的离散计分值Table 6 Value of discrete points of lower membership function At α=0

表7 α=0.5时下隶属函数的离散计分值Table 7 Value of discrete points of lower membership function At α=0.5

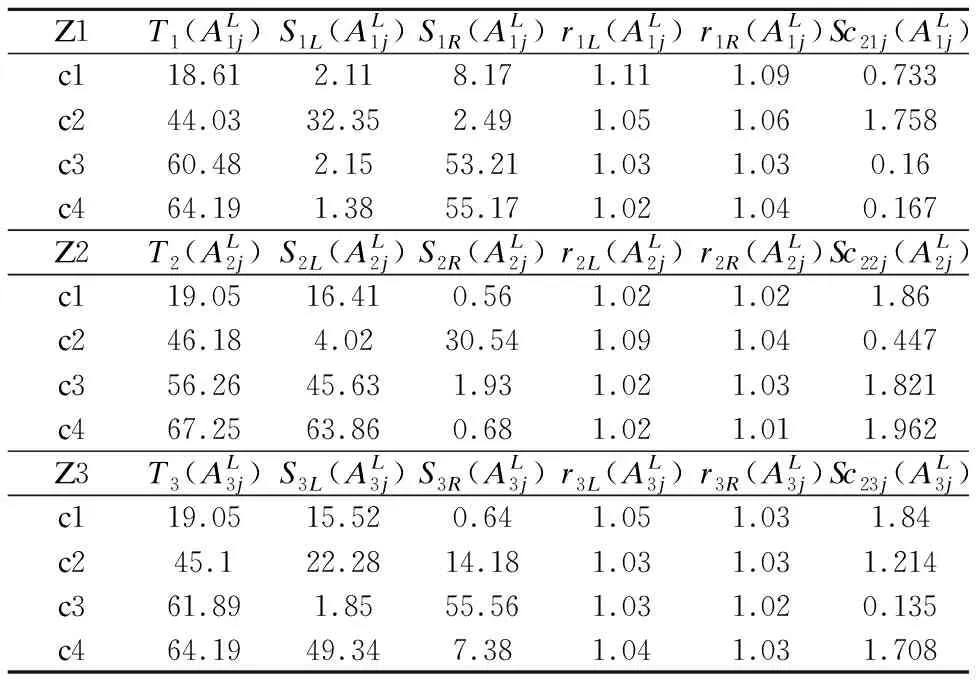
表8 α=1时下隶属函数的离散计分值Table 8 Value of discrete points of lower membership function At α=1

按公式(24)计算出在不同风险态度下的各方案各属性的综合比较计分值Scij,所得结果如表9所示.

表9 综合比较计分值矩阵Table 9 Systematic comparison score value matrix

按公式(25)计算出在不同风险态度下的的各方案的综合比较计分值WAA(Sci),所得结果如表10所示.

表10 各方案综合比较计分值矩阵Table 10 Systematic comparison score value matrix in every Scheme

4.2 比较分析

为了证明本文方法的有效性,与文献[6]以及文献[20] 的结果进行了比较.其中,文献[6]采用传统α截集方法,文献[20]为本文数据的来源.三者比较结果如表11所示.

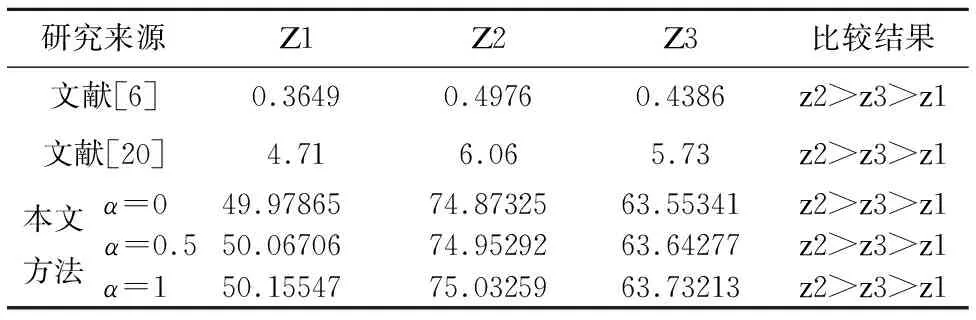
表11 三种方法的结果比较Table 11 Comparing the results of three methods

为了更加直观的比较三种方法结果的差异,将上表数据结果标准化为相同量级后,绘制成折线图,如图3所示.

图3 三种方法结果对比图Fig.3 Comparison diagram of the results of three methods

首先,从表11的比较结果分析,三种方法所得结论相同,证明了方法的有效性;其次,通过表中数据以及图3不难发现,本文方法在方案的区分度上优于其他两种方法,主要原因是本文充分挖掘了隶属函数中的信息,尤其是隶属程度较高的核心区域以及体现模糊不确定性的离散区域的信息,并且在不同数量级上对两者进行计分,使得能够在保证正确区分大小的基础上,从结果中更加显著、直观的了解到隶属程度与模糊不确定程度.因此,本文方法更加合理、更符合实际决策需要,进而降低了决策的风险.

5 结束语

本文提出了一种在高度不确定环境下进行多准则群体决策的方法.该方法从充分挖掘隶属函数中隶属信息和模糊不确定信息的角度出发,提出群决策发生算法完成由多个个体决策到群体决策的转换;再综合重心比较法、截集比较法、聚合算子等原理,构造出针对梯形区间二型模糊隶属函数的深层次比较法.本文构造的比较法不仅在计算过程中分别采用更有针对性的方法进行比较,同时在聚合后的结果中也可以清楚的把握两者间的区别和联系,因而能够得到更加可靠、有依据的决策支持数据,降低了决策的风险,最终得出更加准确、更加合理的决策结果.若进一步进行研究,针对模糊不确定性信息对决策结果影响程度较大的问题,可将离散计分值赋较高权重,以突显其影响力;或根据计分值不同数量级的比较情况,解决支持度和确信度之间的权衡问题.

：

[1] Mendel Jerry M,Hagras Hani,Bustince Humberto,et al.Comments on “interval Type-2 fuzzy sets are generalization of interval-valued fuzzy sets:towards a wide view on their relationship”[J].IEEE Transactions on Fuzzy Systems,2016,24(1):249-250.

[2] Chen Shyi-Ming,Chen Jim-Ho.Fuzzy risk analysis based on ranking generalized fuzzy numbers with different heights and different spreads[J].Expert Systems with Applications,2009,36(3):6833-6842.

[3] Chen Shyi-Ming,Lee Li-Wei.Fuzzy multiple attributes group decision-making based on the interval type-2 TOPSIS method[J].Expert Systems with Applications,2010,37(4):2790-2798.

[4] Celik Erkan,Gul Muhammet,Aydin Nezir,et al.A comprehensive review of multi criteria decision making approaches based on interval type-2 fuzzy sets[J].Knowledge-Based Systems,2015,85:329-341.

[5] Chen Shyi-Ming,Hong Jia-An.Fuzzy multiple attributes group decision-making based on ranking interval Type-2 fuzzy sets and the TOPSIS method[J].IEEE Transactions on Systems Man Cybernetics-Systems,2014,44(12):1665-1673.

[6] Chen Shyi-Ming,Wang Cheng-Yi.Fuzzy decision making systems based on interval type-2 fuzzy sets[J].Information Sciences,2013,242:1-21.

[7] Chen Ting-yu,Chang Chien-hung,Rachel Lu Jui-fen.The extended QUALIFLEX method for multiple criteria decision analysis based on interval type-2 fuzzy sets and applications to medical decision making[J].European Journal of Operational Research,2013,226(3):615-625.

[8] Heidarzade Armaghan,Mahdavi Iraj,Mahdavi-Amiri Nezam.Supplier selection using a clustering method based on a new distance for interval type-2 fuzzy sets:A case study[J].Applied Soft Computing,2016,38:213-231.

[9] Kahraman Cengiz,öztayi Baʂar,Uçal Sarrem,et al.Fuzzy analytic hierarchy process with interval type-2 fuzzy sets[J].Knowledge-Based Systems,2014,59:48-57.

[10] Keshavarz Ghorabaee Mehdi.Developing an MCDM method for robot selection with interval type-2 fuzzy sets[J].Robotics and Computer-Integrated Manufacturing,2016,37:221-232.

[11] Qin Jin-dong,Liu Xin-wang.Multi-attribute group decision making using combined ranking value under interval type-2 fuzzy environment[J].Information Sciences,2015,297:293-315.

[12] Mendel Jerry M,Rajati Mohammad R,Sussner Peter.On clarifying some definitions and notations used for type-2 fuzzy sets as well as some recommended changes[J].Information Sciences,2016,340:337-345.

[13] Wu Dong-rui,Mendel Jerry M.Aggregation using the linguistic weighted average and interval type-2 fuzzy sets[J].IEEE Transactions on Fuzzy Systems,2007,15(6):1145-1161.

[14] Mendel Jerry M.On KM algorithms for solving Type-2 fuzzy set problems[J].IEEE Transactions on Fuzzy Systems,2013,21(3):426-446.

[15] Bozdag Erhan,Asan Umut,Soyer Ayberk,et al.Risk prioritization in failure mode and effects analysis using interval type-2 fuzzy sets[J].Expert Systems with Applications,2015,42(8):4000-4015.

[16] Liu Zhi-qiang,Xu Ruo-ning.A new similarity measure of generalized trapezoidal fuzzy numbers[J].Journal of Guangzhou University(Natural Science Edition),2012,11(6):16-22.

[17] Aziz-Zadeh Lotfi.Fuzzy Sets,Information and control[J].Information and Control,1965,8(3):338-353.

[18] Guo Yong-hui,Shang Zhan-wei,Zou Jun-guo,et al.A comprehensive review of key research on group decision[J].Statistics and Decision,2016,(24):63-67.

[19] Wang Jian-qiang,Peng Lu,Zhang Hong-yu,et al.Method of multi-criteria group decision-making based on cloud aggregation operators with linguistic information[J].Information Sciences,2014,274:177-191.

[20] Chen Ting-yu.Likelihoods of interval type-2 trapezoidal fuzzy preference relations and their application to multiple criteria decision analysis[J].Information Sciences,2015,295:303-322.

附中文参考文献：

[16] 刘志强,许若宁.一种新的基于重心的广义梯形模糊数相似性测度[J].广州大学学报(自然科学版),2012,11(6):16-22.

[18] 郭永辉,尚战伟,邹俊国,等.群决策关键问题研究综述[J].统计与决策，2016,(24):63-67.