邻域粗糙集中基于序列的混合型属性离群点检测
袁 钟,张贤勇,冯 山
1(四川师范大学 数学与软件科学学院,成都 610068)
2(四川师范大学 智能信息与量子信息研究所,成都 610068)
1 引 言
离群点(也称异常点)是数据集中偏离大部分对象的数据点[1].离群点检测在欺诈检测、医疗处理、公共安全、工业损毁检测、图象处理、视频网络监视以及入侵检测等诸多领域都具有十分重要的作用[2-4].现有的离群点检测方法主要有4类:(1) 基于统计的[5];(2) 基于邻近性的[6-8](包括基于距离的、基于网格和基于密度的);(3) 基于聚类的[9];(4)基于粗糙集的[10].
经典粗糙集方法基于等价关系和等价类,其检测模型仅适用于符号型属性而非数值型属性数据集.这类方法对数值型属性数据集处理时必须进行符号化处理,从而增加数据处理时间,并伴有影响检测精度的信息损失.
为了处理数值型属性数据,文[11]提出邻域粗糙集的概念.但是,目前在邻域粗糙集模型中对于离群点检测的研究还很少[12,13].本文将回顾邻域和邻域粗糙集的基本概念,提出基于序列的混合型属性离群点检测方法.该方法通过每个属性值的均匀性来构建属性序列,以此定义属性集序列并定义邻域类序列.进一步通过分析邻域类序列中对象的变化情况来检测离群点,并设计出相应的离群点检测算法(Sequence-based Mixed Attribute Outlier Detection,SMAOD).所建方法拓展了传统粗糙集方法,同时适用于符号型、数值型和混合型属性数据集.在UCI标准数据集上与主要的一些离群点检测方法进行了实验比较分析,结果表明所提出的方法具有更好的适应性和有效性.
2 邻域粗糙集

对∀x,y,z∈U.关联于B的距离函数dB:U×U→R+(R+是非负实数集)应满足:
(1)dB(x,y)≥0(非负性);
(2)dB(x,y)=dB(y,x)(对称性);
(3)dB(x,z)≤dB(x,y)+dB(y,z)(三角不等式).
对于B={ci1,ci2,…,cik},1≤k≤m,dB的闵可夫斯基距离表示为:
基于距离度量,可引入邻域半径ε来粒化论域U,形成邻域关系及邻域类,以便构建邻域信息系统.
定义1[14].(邻域)对∀x∈U和ε≥0,x在属性集B上的ε-邻域定义为:
(1)
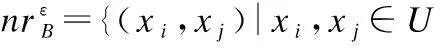


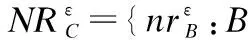
3 基于序列的混合型属性离群点检测方法
在文献[10]中,给定一个信息系统,为条件属性集的每个属性指派一个均匀性,并且通过每次从条件属性集中去掉均匀性最大的那个属性,来观察U中每个对象所属的等价类的变化情况,进而构建序列离群因子来表征每个数据对象的离群程度.但是,该方法主要基于等价关系和等价类来建模,其检测模型适用于符号型属性而非数值型属性数据集.对此,本节在文献[10]基础上进行有效拓展,主要采用邻域粗糙集的邻域关系和邻域类来建模,相关结果广泛适用于符号型、数值型和混合型属性数据集.
利用邻域粗糙集数据处理时,数据对象的描述通常会存在量级和量纲的差异.为得到精确的数据处理结果,避免不同数据之间的影响,要先对原始数值型属性值进行归一化处理[15],本文采用最小-最大标准化.其计算公式如下:
(2)
其中,maxcj和mincj分别为U中关于属性cj的最大值和最小值.标准化后,这些属性的属性值的范围为[0,1].
为有效处理数值型和混合型属性数据集,文[16]提出了混合欧氏重叠度量(HEOM).相仿,可定义如下的混合曼哈顿重叠度量(Heterogeneous Manhattan-Overlap Metric,HMOM).
定义5.(HMOM距离)对象x,y∈U的混合曼哈顿重叠度量HMOMB(x,y)定义为:
(3)
其中,
从上述定义可以看出,HMOM函数不仅可以处理数值型属性数据集,而且可以处理数值型和符号型属性相结合的复杂数据集,当部分属性值未知时也可以使用.因此,本文采用HMOM函数作为邻域距离,这为应用范围拓展奠定了基础.
邻域涉及邻域半径的选取.传统的邻域半径ε一般是专家根据经验给定.显然,这样的处理方法具有主观性和随机性,会导致算法的参数选取特敏感.为此,本文将对象x在属性cj的邻域半径设为:
(4)
其中,std(cj)是cj的属性值标准差,预设参数λ用于调整邻域大小.这为后续检测方法的有效性奠定了基础.
标准差用于衡量数据的均值分散程度.标准差较大表示大部分数据对象值和其均值之间差异较大;标准差较小表示数据对象值较接近均值.因此,标准差可以此作为调整邻域半径的一个重要因素.这里,λ的作用是根据标准差调整邻域大小.当λ<1时,邻域半径大于属性值的标准差;当λ=1时,邻域的半径即为属性值的标准差;当λ>1时,邻域半径小于属性值的标准差.
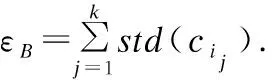
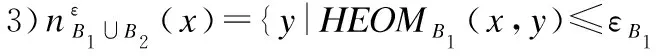
由此,可基于距离度量计算对象邻域以得到邻域关系和邻域类,从而构建邻域信息系统.
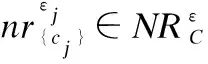
定义6.(属性的均匀性)给定λ>0,属性cj的均匀性Var(cj)定义为:
(5)
关联于统计方差,Var(cj)衡量对象在属性cj上的离散程度,揭示了对象内部彼此波动的程度.通过计算出C中每个属性的均匀性,就可以将C中的所有属性按照均匀性进行排序,从而得到一个属性序列.
定义7.(属性序列)属性序列S定义为:
(6)
进一步由属性集C开始,每次从中去除均匀性最大的那个属性,直到得到一个只包含一个属性的集.这样,就可以确定一个属性集序列.
定义8.(属性集序列)属性集序列CS定义为:
CS=
(7)
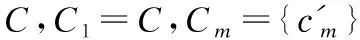
属性集序列CS中每个属性集都可以确定一个邻域关系,这样就得到对象x的m个邻域类.由此,可以构造相应的邻域类序列.
定义9.(邻域类序列)对象x的邻域类序列NS(x)定义为:
(8)
基于上述三种序列的定义,类似于Breunig等的做法[8],下面提出邻域序列离群因子的概念来表征对象的离群程度.
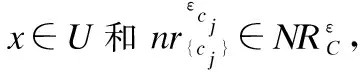
(9)
定义11.(邻域序列离群点)给定λ>0,令μ为一个给定的阈值.对于∀x∈U,NSOF(x)>μ,则x被称为U中的一个邻域序列离群点.
定义10通过邻域类序列建立了邻域序列离群因子,用于刻画对象的离群程度.进而,定义11基于判定阈值,自然进行离群点检测.
一般情况下,离群点检测方法只给出了每个对象的离群程度;在使用该方法来检测离群点之前,用户应该首先输入一个经验值k来表示他们期望的离群点的个数.在定义11所述离群点检测方法中,参数μ的设置也取决于用户提供的k值.首先,可以计算每个对象x的离群因子,并把这些对象根据其离群因子从大到小排序;进而,由此设置阈值μ,确保找到k个对象使其离群程度在U中高于其他对象;最后,这k个对象将作为离群点返回给用户.
4 基于序列的混合型属性离群点检测算法SMAOD
基于上述离群点检测方法,本节提出基于序列的混合型属性离群点检测算法(SMAOD)(算法2).特别地,算法2调用了单属性邻域覆盖算法(Single Attribute Neighborhood Covering,SANC)(算法1),而算法1改进了传统的逐一比较的计算模式.
算法1.计算单属性邻域覆盖SANC
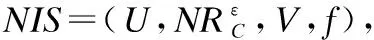
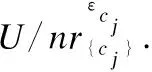
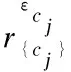
(2)N←φ;
(3) [Rank,Index]←Ascend_sort(U);
/*据属性cj对U中对象升序排列,其中Rank保存排列结果,Index保存对应的原始顺序*/
(4)fori←1 tondo
(5)k←i;
(6)whilek>0do
(7)ifHEOM{cj}(Rank[i],Rank[k])≤εcjthen
(8)k←k-1;
(9)else
(10) break;
(11)endif
(12)endwhile
(13)a←k+1;/*用a记录对象邻域的下限序号*/
(14)k←i+1;
(15)whilek (16)ifHEOM{cj}(Rank[i],Rank[k])≤εcjthen (17)k←k+1; (18)else (19) break; (20)endif (21)endwhile (22)b←k-1;/*用b记录对象邻域的上限序号*/ (23)N←Rank[a…b]; (25)endfor 算法1中第3步使用由Williams等人提出的堆排序法[17],它的时间复杂度为O(nlogn),改进了通常的排序时间复杂度O(n2).第4步的频度为n,第5-24步的频度为n.所以第4-25步频度为n×n.因此,在最坏的情况下,SANC算法的时间复杂度为O(n2),与传统逐一比较算法的时间复杂度一致.但是,由于SANC算法基于排序结果进行邻域计算,对象的每个属性的取值等概率分布,则在平均情况下,SANC算法的第4-25步平均比较次数接近n,它远比传统的逐一比较计算方法的比较次数n×n低.综上,SANC算法的实际时间复杂度为O(nlogn),表明算法1优于传统逐一比较计算模式的时间复杂度O(n2). 算法2.基于序列的混合型属性离群点检测算法 SMAOD 输出:邻域序列离群点集OS. (1)OS←φ; (2)forj←1 tomdo (4) 计算Var(cj); (5)endfor (7)构造属性集序列CS= (8)forj←1 tomdo (10)endfor (11)fori←1 tondo (12) 构造邻域类序列 (13) 计算W(xi); (14) 计算NSOF(xi); (15)ifNSOF(xi)>μthen (16)OS←OS∪{xi}; (17)endif (18)endfor (19)returnOS. 下面分析算法2.由算法1知,第2-5步的频度为m×n×logn;第8-10步的频度为m×n2;第11-18步的频度为n.所以算法2的频度为m×n×logn+m×n2+n.因此,算法2的时间复杂度为O(mn2),空间复杂度为O(mn). 本节主要比较SMAOD算法、NED算法[12]、SEQ算法[10]、基于距离的离群点检测方法[6]和KNN算法[18]的性能.为了测试SMAOD算法的有效性,这里选取三种UCI数据集[19]进行实验,它们是:Annealing数据集(混合型属性)、Wisconsin Breast Cancer数据集(数值型属性)和Lymphography数据集(多数为符号型属性).其中,在Annealing数据集上,将比较SMAOD算法、NED算法、基于距离的离群点检测方法和KNN算法的性能,在Wisconsin Breast Cancer和Lymphography数据集上,将比较SMAOD算法、NED算法、SEQ算法、基于距离的离群点检测方法和KNN算法的性能. 为了增强实验结果的可比性,本文采用目前最常用的一种离群点检测方法评价体系[20]来评测各算法的性能.具体地,给定一个数据集以及数据集中每个对象所属的类,通过在该数据集上运行该算法,并且计算在由该算法所找出的离群点中,真正的离群点所占比越高,则表明该算法的性能越好. Annealing数据集中包含798个对象,37个条件属性和1个决策属性.其中条件属性包括30个符号型属性和7个数值型属性.798个对象被分为5类,类3包含最多的对象数,把余下的类看作稀有类,总共190个离群点(即属于稀有类的对象数).相关的邻域信息系统记为NISA.对于SMAOD算法,设置λ=0.3(其主要由数据实验而设定).具体的实验结果如表1所示. 表1 邻域信息系统NISA上的实验结果Table 1 Experimental results in NISA 在表1中,|RUA|表示UA中离群点的个数,“DIS”代表基于距离的离群点检测方法.对于数据集中每个对象x,分别利用这四种离群点检测方法来计算x的离群程度值.然后根据每种方法所计算出的数据集中对象的离群程度值,由高到低对数据集中对象进行排序.由此,表1中“离群程度值前k%的对象(对象数)”是指在采用某种离群点检测方法来计算数据集中对象的离群程度值之后,离群程度值排在前k%的对象以及这些对象的个数;“属于稀有类的对象数”则是指在由该方法所检测出的离群程度值排在前k%的对象中属于稀有类的对象个数;“覆盖率”是指这些属于稀有类的对象占数据集中所有离群点的比例. 图1 邻域信息系统NISA上的实验结果折线图Fig.1 Line chart of experimental results in NISA 表1可见,在Annealing数据集中SMAOD算法具有最好的性能.SMAOD算法的准确率高于其它方法.例如,当离群程度前10.03%(对象数为80),SMAOD算法检测离群点的数目是60,即由SMAOD算法检测出的60个对象是Annealing数据集中的离群点,但对NED、DIS和KNN算法分别只检测出51、33和21个离群点.这说明SMAOD算法在Annealing数据集上的有效性.为了更加形象,这四种算法的实验结果(表1)也用折线图描绘于图1,其更明显地展现了SMAOD算法优于其它算法.此外,Annealing数据集不仅具有符号型属性数据,而且还具有连续性数值型属性数据.因此,实验结果也表明,SMAOD算法适用于混合型属性数据集. Wisconsin Breast Cancer数据集中包含699个对象,9个数值型属性.所有对象被分成两类:“benign”(65.5%)和“malignant”(34.5%).为了形成一个非常不均匀的分布,我们仿照Harkins等的做法[21],从该数据集中移去一些属于“malignant”类的对象.最终的数据集包括483个对象,其中39个对象属于“malignant”类,444个属于“benign”类,相关的邻域信息系统记为NISW. 表2 邻域信息系统NISW上的实验结果Table 2 Experimental results in NISW 在最终的Wisconsin Breast Cancer数据集中,将“malignant”类看作离群点.对于SMAOD算法,我们设置λ=2.具体实验结果如表2和图2所示. 图2 邻域信息系统NISW上的实验结果折线图Fig.2 Line chart of experimental results in NISW 从表2和图2中可以看到,对于Wisconsin Breast Cancer数据集,SMAOD算法的性能比其它的离群点检测方法的性能好.Wisconsin Breast Cancer数据集9个属性全为数值型属性,这说明SMAOD算法在处理全是数值型属性的数据时也有很好效果. Lymphography数据集中包含148对象、18个条件属性和1个决策属性,其中条件属性有3个数值型属性,15个符号型属性.所有的对象被决策属性分成四个类:“normal find”(1.35%)、“metastases”(54.73%)、“malign lymph”(41.22%)和“fibrosis”(2.7%).将“normal find”和“fibrosis”看作离群点,总共有6个离群点(即属于稀有类的对象数).相关邻域信息系统记为NISL.对于SMAOD算法,设置λ=0.2.具体实验结果如表3和图3所示. 从表3和图3中可以看到,对于Lymphography数据集,SMAOD算法的性能比其它的离群点检测方法的性能好.Lymphography数据集多数为符号型属性,因此SMAOD算法也适用于符号型属性数据. 表3 邻域信息系统NISL上的实验结果Table 3 Experimental results in NISL 图3 邻域信息系统NISL上的实验结果折线图Fig.3 Line chart of experimental results in NISL 离群点检测在许多领域中具有重要作用.针对传统粗糙集的离群点检测方法难以处理数值型属性数据的缺陷,提出邻域粗糙集中基于序列的混合型属性离群点检测方法.相关方法采用每个属性值的均匀性构建属性序列,以此定义属性集序列,从而定义邻域类序列.进一步通过分析邻域类序列中对象的变化情况来检测离群点,并设计出相应的离群点算法SMAOD.该方法拓展了传统粗糙集方法,同时适用于符号型、数值型和混合型属性数据集.在UCI标准数据集上与现有的一些离群点检测方法进行了实验的比较分析,实验结果表明所提方法具有更好的适应性和有效性.对此,相关的检测机制主要得益于HMOM混合距离选择、标准差方差的统计使用、多级序列构造等.由于利用邻域粗糙集的方法进行离群点检测的研究还比较少见,本文的工作拓展了邻域粗糙集在数据挖掘等领域的应用范围,为混合型属性离群点检测提供了一点思路.在未来的工作中,为减少算法运行时间复杂度,可考虑在离群点检测之前,先对数据集进行属性约简或特征选择. : [1] Hawkins D.Identification of outliers [M].London:Chapman and Hall,1980:1-2. [2] Ge Qing-long,Xue An-rong,Jia Xiao-yan.Relevant subspace based outlier mining [J].Journal of Chinese Computer Systems,2015,36(5):1028-1032. [3] Yang Jin-hong,Deng Ting-quan.A one-cluster kernel PCM based SVDD method for outlier detection[J].Acta Electronica Sinica,2017,45(4):813-819. [4] Han J W,Kamber M,Pei J.Data mining:concepts and techniques third edition [M].San Francisco:Morgan Kaufmann,2011:543-583. [5] Rousseeuw P J,Leroy A M.Robust regression and outlier detection [M].New York:John Wiley & Sons,1987:1-18. [6] Knorr E,Ng R,Tucakov V.Distance-based outliers:algorithms and applications [J].The VLDB Journal,2000,8(3-4):237-253. [7] Knorr E,Ng R.A unified notion of outliers:properties and computation [C].In International Conference on Knowledge Discovery & Data Mining,1997:219-222. [8] Breunig M M,Kriegel H P,Ng R T,et al.LOF:identifying density-based local outliers [C].Proc of the ACM SIGMOD Int Conf on Management of Data,Dallas:ACM Press,2000:93-104. [9] Jain A K,Murty M N,Flynn P J.Data clustering:a review [J].ACM Computing Surveys,1999,31(3):264-323. [10] Jiang F,Sui Y F,Cao C G.Some issues about outlier detection in rough set theory [J].Expert Systems with Applications,2009,36(3):4680-4687. [11] Lin T Y.Neighborhood systems-application to qualitative fuzzy and rough sets [C].Advances in Machine Intelligence and Soft-computing,Durham:Department of Electrical Engineering,1997:132-155. [12] Chen Y M,Miao D Q,Zhang H Y. Neighborhood outlier detection [J].Expert Systems with Applications,2010,37(12):8745-8749. [13] Li X J,Rao F.Outlier detection using the information entropy of neighborhood rough sets[J].Journal of Information & Computational Science,2012,12(9):3339-3350. [14] Hu Q H,Yu D R,Liu J F,et al.Neighborhood rough set based heterogeneous feature subset selection [J].Information Sciences,2008,178(18):3577-3594. [15] Kennedy R L,Lee Y,Van Roy B,et al.Solving data mining problems through pattern recognition [M].Prentice Hall PTR,1997. [16] Wilson D R,Martinez T R.Improved heterogeneous distance functions [J].Journal of Artificial Intelligence Research,1997,6(1):1-34. [17] Williams J.Algorithm 232 (heapsort)[J].Communications of the ACM,1964,7(6):347-348. [18] Ramaswamy S,Rastogi R,Shim K.Efficient algorithms for mining outliers from large datasets [C].Proc of the 2000 ACM SIGMOD Int Conf on Management of Data,Dallas:ACM Press,2000:427-438. [19] Bay S D.The UCI KDD repository[DB/OL].http://kdd.ics.uci.edu,2016-05-12. [20] Aggarwal C C,Yu P S.Outlier detection for high dimensional data [C].In Proc of the 2001 ACM SIGMOD Int Conf on Management of Data,Califomia:ACM Press,2001:37-46. [21] Harkins S,He H,Williams G,et al.Outlier detection using replicator neural networks [C].Proc of the 4th Int Conf on Data Warehousing and Knowledge Discovery,Aix-en-Provence:Springer-Verlag,2002:170-180. 附中文参考文献: [2] 葛清龙,薛安荣,贾小艳.关联子空间离群点挖掘 [J].小型微型计算机系统,2015,36(5):1028-1032. [3] 杨金鸿,邓廷权.一种基于单簇核PCM的SVDD离群点检测方法[J].电子学报,2017,45(4):813-819.

5 实验结果与分析
5.1 Annealing 数据集
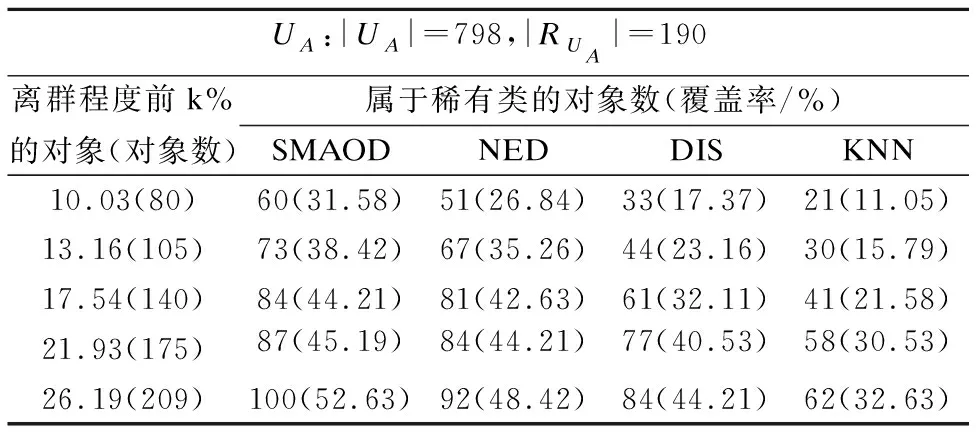

5.2 Wisconsin Breast Cancer数据集


5.3 Lymphography数据集
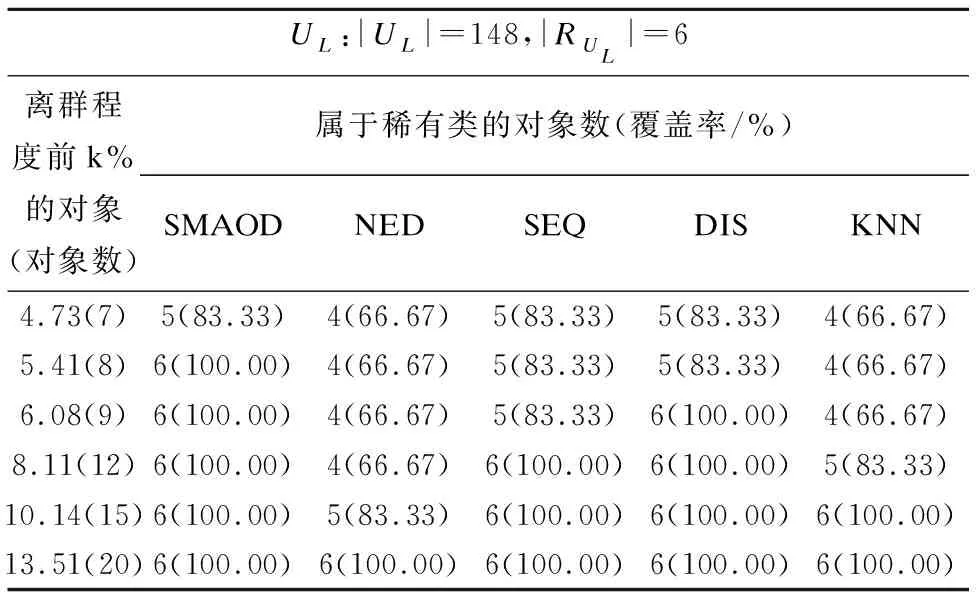
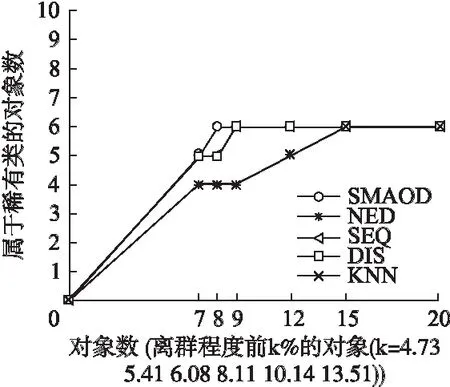
6 结 论

