时变公路网络的动态路径规划算法
许祎娜,王旭仁,2,苏红莉
1(首都师范大学 信息工程学院,北京 100048)
2(中国科学院信息工程研究所 中国科学院网络测评技术重点实验室,北京 100093)
1 引 言
最短路径算法诞生于运筹学和计算机科学,是图论的经典算法.通过数据结构等计算机技术可将很多其它领域的实际问题抽象成运筹学中的最短路径问题(Shortest Path,SP),如交通路径规划等.Dijkstra算法[1]在求解点对点的最短路径时,遍历的节点较多,效率较低.受人工智能等思想的启示,许多相关的启发式加速方案及其改进算法不断涌现[2,3],并在大规模网络的路径规划问题中获得了较好的成果,例如结合目标导向、双向搜索、预处理技术、分层思想或剪枝技术等方式加速最短路径的搜索效率[4-10].
传统最短路径模型都是基于静态网络结构,即形式化网络图的结构已知,且弧(或边)的权值不变.然而在实际的交通路网中,各弧边的权重会随时间发生变化,比如道路的通行力及车速会受到交通状况等动态因素的影响而有所变动.利用最短路径树[11,12]的结构特性,当网络发生变化时,只对受影响的节点进行更新操作,进而可以获取更好的动态更新时间效率.本文的主要工作是以基于地标的三角启发算法(A* Landmarks Triangle,ALT)[5]和动态最短路径树算法(Dynamic Shortest Path Tree,DSPT)[12]为基础,研究如何在随时间变化的公路网络中进行两点之间最短路径的查询.
2 相关研究
对于时变网络(Time-Dependent Networks,TDN,亦称时间依赖网络),许多研究者通过改进Dijkstra算法等经典算法来求解TDN网络的SP问题.Kaufman和Smith[13]指出改进的经典SP算法仍具有局限性,但通过建立严格的一致性条件,经典SP算法可以求解满足先入先出特性的TDN网络SP问题.基于此,文献[8]结合A*算法和双向搜索技术求解此类问题.
A*算法[4]由Hart等人提出,是求解静态网络SP问题最流行最有效的启发式直接搜索算法,主要是通过建立具有导向性的估价函数(potential function)来减少算法的搜索空间,从而提高搜索效率.Goldberg等[5]通过结合数据预处理技术和三角不等式原理来计算A*算法中的估价函数值,提出了一种基于地标的A*算法,即ALT算法,又称为三角启发算法.ALT算法首先从道路网络中选取一定数量的节点作为地标(landmark),预先计算并存储每个地标与所有节点之间的最短路径距离,然后应用三角不等式原理使查询路径趋向于目标节点.
虽然双向ALT算法可以求解TDN网络的SP问题,但当TDN网络中某边更新后的权值小于初始权值时,需要重新计算预处理数据,会产生大量不必要的更新操作.通过结合ALT算法和最短路径树的方式[14,15],不仅可以实现网络的动态更新,而且能够减少预处理数据的更新操作代价.文献[12]提出了可动态更新网络的DSPT算法,首先使用Dijkstra算法建立最短路径树,当TDN网络的边权值发生变化时,根据变化边为受影响的节点和边构建队列,根据队列计算并更新最短路径树中的边和节点,避免了全局更新.但该算法会造成大量节点和边多次更新的冗余计算,且最短路径树的占用空间较大,并不适用于大规模网络.
此外,近期的研究工作中提出了几种新型最短路径算法,例如动态时变网络最短路径(Dynamic Time-Dependent Shortest Path,DTDSP)算法[16]和时延神经网络(Time-Delay Neural Network,TDNN)算法[17].其中,DTDSP算法提出了一种可根据当前道路状况动态更新速度的线性变化模型,并根据不同的路况提供不同的最优路径.TDNN算法将网络中的每一个节点当作一个神经元,使用并行计算和反馈机制求解出一个全局最短路径.这两种算法均得到了较好的查询效率,但算法所构造的网络模型均要求网络的拓扑变化具有确定性.
本文在满足时间一致性条件[13]的前提下,结合DSPT算法的局部更新思想与ALT算法的目标导向技术和预处理技术,针对上述DSPT算法和ALT算法的不足之处,以时变公路网络(Time-Dependent Road Networks,TDRN)为研究载体,提出了一种基于动态最短路径树的地标导向启发式算法(Dynamic A* Landmarks Triangle,DALT),构造地标的最短路径树,并对TDRN网络的动态更新策略和点对点的启发式路径规划展开研究.
3 网络模型及理论基础
将不含负权边的TDRN网络抽象表示为拓扑图G=(V,E,W),其中V表示节点集合,E表示边集合,W表示边的权值集合,并有地标集L⊆V.对于任意集合N,|N|表示集合N中的元素个数.为了方便描述,本文给出如下定义和性质:
定义1.连边e=(i,j)∈E表征以节点i为起点、节点j为终点所对应的路段,S(e)和D(e)分别表征连边e的起点和终点,w(e)表征边e的权值,w′(e)表征边e发生变化后的权值.
定义2.对于任意节点n∈V,I(n)={e∈E|D(e)=n}表征节点n的入度边集合,O(n)={e∈E|S(e)=n}表征节点n的出度边集合.
定义3.Dist(s,t)表征从节点s出发到达节点t的最短路径,d(s,t)表征对应的最短路径值.Dist(s,t)与Dist(t,s)并不等价,且d(s,t)与d(t,s)也不一定相等.
定义4.SPT(s,t)表征最短路径树SPT中,从节点s出发到达节点t的路径.SPT(s,t)与SPT(t,s)并不等价.
定义5.设l.FSPT为一棵以地标节点l∈L为根的最短路径树,从根节点l到树中任意节点n的路径FSPT(l,n)均为最短路径Dist(l,n),对应的最短路径值为d(l,n).对于节点i∈l.FSPT,sub(i)表征l.FSPT中节点i的子孙节点集合且包含节点i,sub(i)中的节点n按d(l,n)升序排列.
定义6.设l.TSPT为一棵以地标节点l∈L为根的最短路径树,从树中任意节点n到根节点l的路径TSPT(l,n)均为最短路径Dist(n,l),对应的最短路径值为d(n,l).对于节点i∈l.TSPT,sup(i)表征l.TSPT中节点i的祖先节点集合且包含节点i,sup(i)中的节点n按d(n,l)升序排列.
定义7.若连边e=(i,j)∈l.FSPT,则称节点i为节点j的父节点,表征为P(j)=i;若连边e=(i,j)∈l.TSPT,则称节点j为节点i的子节点,表征为C(i)=j.
性质1.若节点i、节点j在同一棵SPT中,且从节点i到节点j存在路径SPT(i,j),则该路径必为最短路径Dist(i,j).
证明:
∀节点i∈l.FSPT,节点j∈l.FSPT,若∃FSPT(i,j),已知:
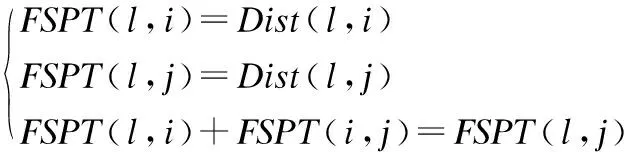
(1)
根据上式可得:
FSPT(i,j) =FSPT(l,j)-FSPT(l,i)
=Dist(l,j)-Dist(l,i)
=Dist(i,j)
(2)
∀节点i∈l.TSPT,节点j∈l.TSPT,若∃TSPT(i,j),同理可得:
TSPT(i,j)=Dist(i,j)
(3)
证毕.
性质2.若节点j∈sub(i),则在l.FSPT中从地标l出发到达节点j必先经过节点i.若节点j∈sup(i),则在l.TSPT中从节点j出发到达地标l必先经过节点i.
证明:
∀节点i∈l.FSPT,节点j∈l.FSPT,若j∈sub(i),则∃FSPT(i,j),根据最短路径唯一和性质1可知必有:
FSPT(l,j)=FPST(l,i)+FSPT(i,j)
(4)
∀节点i∈l.TSPT,节点j∈l.TSPT,若j∈sup(i),则∃TSPT(i,j),同理可知必有:
TSPT(j,l)=FPST(j,i)+FSPT(i,l)
(5)
证毕.
综上所述,求解点对(s,t)的最短路径问题的数学模型表示为:
mind(s,t)=∑e∈Dist(s,t)w(e)
(6)
4 DALT算法描述
TDRN网络会在某一时刻发生变化,如边的插入或删除、边权值的增加或减小.由于边的插入可处理为边权值从无穷大到有限值,而对于边的删除则可处理为边权值从有限值到无穷大.因此DALT算法只讨论边权值的变化,并假设两点之间的最短路径唯一,主要内容如下:
1)选取地标集后,在预处理阶段为各个地标生成两个动态最短路径树,分别存储该地标到其它节点的最短路径及其距离、其它节点到该地标的最短路径及其距离,具体过程见4.1.1.
2)当网络中某边的权值发生变化时,执行DALT算法的更新策略,具体过程见4.1.2.
3)当进行路径规划查询时,使用基于预处理数据的启发式算法搜索最短路径,具体过程见4.2.
4.1 基于动态最短路径树的数据预处理及更新
4.1.1 构造地标的动态最短路径树
当选取一定数量的节点作为地标并加入地标集L后,对每个地标节点l进行步骤1和步骤2,在SPT的构造过程中使用两个队列openQueue和closedQueue分别存放当前待处理的节点和已经计算出最短路径的节点,并用shortestNode和shortestValue记录上一个计算出最短路径的节点及其路径值,shortestValue无穷大则表示节点shortestNode不可达.
步骤1.构造地标l的FSPT
首先将shortestNode加入l.FSPT和closedQueue,根据shortestNode的出度边集合O(shortestNode)依次将出度边的终点n加入openQueue并更新d(l,n)及其父节点P(n),初始状态下shortestNode即为地标l,shortestValue的值为0;然后计算openQueue中当前距离地标l最近的节点并更新shortestNode和shortestValue;重复以上操作直至最后一个可达节点加入closedQueue.
具体构造方法如下:
Algorithm1.构造地标l的FSPT
1.d(l,l)= 0;
2.shortestNode=l;
3.shorestValue=0;
4.closedQueue.add(shortestNode);
5.l.FSPT.add(shortestNode);
6.whileshorestValue≠∞
7.shortestValue=∞;
8. /*更新队列openQueue及其各节点的距离*/
9.for∀e=(i,n)∈O(shortestNode)
10.ifn∉closedQueueandn∉openQueue
11.d(l,n)=d(l,i)+w(e);
12.P(n)=i;
13.openQueue.add(n);
14.elseifn∈openQueueandd(l,n)>d(l,i)+w(e)
15.d(l,n)=d(l,i)+w(e);
16.P(n)=i;
17.openQueue.update(n);
18.endif
19.endfor
20. /*计算当前openQueue中距离最小的节点*/
21.shortestNode=minn{d(l,n)|n∈openQueue};
22.shortestValue=d(l,shortestNode);
23. /* 如果节点shortestNode可达 */
24.ifshorestValue≠∞
25.openQueue.remove(shorestNode);
26.closedQueue.add(shortestNode);
27.l.FSPT.add(shortestNode);
28.endif
29.endwhile
步骤2.构造地标l的TSPT
首先将shortestNode加入l.TSPT和closedQueue,根据shortestNode的入度边集合I(shortestNode)依次将入度边的起点n加入openQueue并更新d(n,l)及其子节点C(n),初始状态下shortestNode即为地标l,shortestValue的值为0;然后计算openQueue中当前距离地标l最近的节点并更新shortestNode和shortestValue;重复以上操作直至最后一个可达节点加入closedQueue.
TSPT与FSPT的构造方法类似,只需在Algorithm 1的基础上替换以下几行算法:
Algorithm2.构造地标l的TSPT(与Algorithm1不同的部分)
5.l.TSPT.add(shortestNode);
9.for∀e=(n,i)∈I(shortestNode)
11.d(n,l) =d(i,l) +w(e);
12.C(n)=i;
14.elseifn∈openQueueandd(n,l)>d(i,l) +w(e)
15.d(n,l) =d(i,l) +w(e);
16.C(n)=i;
21.shortestNode=minn{d(n,l)|n∈openQueue};
22.shortestValue=d(shortestNode,l);
27.l.TSPT.add(shortestNode);
4.1.2 更新地标的动态最短路径树
当边e=(i,j)∈E的权值增加时,若e∉SPT,则不需要对SPT进行更新;否则对SPT中受影响的节点进行更新.当边e=(i,j)∈E的权值减小时,对于地标l,若d(l,i)+w′(e) 根据性质2可知,l.FSPT中受影响的节点必包含sub(j),l.TSPT中受影响的节点必包含sup(i).在权值增加的更新操作中,只需要对sub(j)或sup(i)中的节点及其连接边进行扫描和权值增量计算,最短路径树中其它节点的最短路径和距离并不受影响;而在权值减少的更新操作中,sub(j)或sup(i)中的节点只需更新一次,但这些节点的权值减少可能使得其它节点获取到一条新的最短路径及其路径,比权值增加的计算过程更为复杂[18].此外,由最短路径唯一可知,FSPT中各节点的父节点唯一,且TSPT中各节点的子节点也唯一,故可根据父节点或子节点更新其直接子孙节点或直接祖先节点. 在对SPT进行更新时,使用队列Q记录受影响的节点及其增量,依次遍历Q中的节点,同时更新各个节点的权值、变化增量及其父节点或子节点,其中在权值减小的更新过程中,为减少冗余计算,使用队列closedQ记录队列Q中已求解最短路径的节点. DALT算法对最短路径树的具体更新策略如下: Algorithm3.-DALT算法的SPT更新 Step1. /*当连边e=(i,j)权值发生变化时 */ 1.ifw′(e)>w(e)ande∈l.FSPT 2.P(j).inc=w′(e)-w(e); 3.Q=sub(j); 4.gotoStep2; 5.endif 6.ifw′(e)>w(e) ande∈l.TSPT 7.C(i).inc=w′(e)-w(e); 8.Q=sup(i); 9.gotoStep3; 10.endif 11.ifw′(e) 12.i.inc=d(l,i)+w′(e)-d(l,j); 13.P(j)=i; 14.Q=sub(j); 15.gotoStep4; 16.endif 17.ifw′(e) 18.j.inc=d(j,l)+w′(e)-d(i,l); 19.C(i)=j; 20.Q=sup(i); 21.gotoStep5; 22.endif Step2. /*当l.FSPT中的连边e=(i,j)权值增加时*/ 1.for∀n∈Q 2. n.inc=P(n).inc; 3. d(l,n)=d(l,n)+n.inc; 4.for∀e∈I(n)andS(e)∉Qandd(l,S(e))+w(e) 5.n.inc=n.inc+d(l,S(e))+w(e)-d(l,n); 6.d(l,n)=d(l,S(e))+w(e); 7.P(n)=S(e); 8.endfor 9.endfor 10.gotoStep1; Step3. /* 当l.TSPT中的连边e=(i,j)权值增加时 */ 1.for∀n∈Q 2. n.inc = C(n).inc; 3. d(n,l) = d(n,l) +n.inc; 4.for∀e∈O(n)andD(e)∉Qandd(D(e),l)+w(e) 5.n.inc=n.inc+d(D(e),l)+w(e)-d(n,l); 6.d(n,l)=d(D(e),l)+w(e); 7.C(n)=D(e); 8.endfor 9.endfor 10.gotoStep1; Step4. /* 当连边e=(i,j)权值减小且l.FSPT受影响时 */ 1.for∀n∈Qandn∉closedQ 2.ifn.inc=0 /*首次更新时根据父节点更新增量和权值*/ 3.n.inc=C(n).inc; 4.d(n,l) =d(n,l) +n.inc; 5.endif 6.for∀e∈O(n)andD(e)∉sub(j)andd(l,n)+w(e) 7.D(e).inc=D(e).inc+d(l,n)+w(e)-d(l,D(e)); 8.d(l,D(e))=d(l,n)+w(e); 9.P(D(e))=n; 10.Q.add(D(e)); 11.closedQ.add(D(e)); 12.for∀m∈sub(D(e))andP(m)=D(e) 13.d(l,m) =d(l,m) +D(e).inc; 14.m.inc=D(e).inc; 15.Q.add(m);/* 将D(e)的直接子孙节点加入Q*/ 16.endfor 17.endfor 18.closedQ.add(n); 19.endfor 20.gotoStep1; Step5. /* 当连边e=(i,j)权值减小且l.TSPT受影响时 */ 1.for∀n∈Qandn∉closedQ 2.ifn.inc=0 /*首次更新时根据子节点更新增量和权值*/ 3.n.inc=C(n).inc; 4.d(n,l) =d(n,l) +n.inc; 5.endif 6.for∀e∈I(n)andS(e)∉sup(i)andd(n,l)+w(e) 7.S(e).inc=S(e).inc+d(n,l)+w(e)-d(S(e),l); 8.d(S(e),l)=d(n,l)+w(e); 9.C(S(e))=n; 10.Q.add(S(e)); 11.closedQ.add(S(e)); 12.for∀m∈sup(S(e))andC(m)=S(e) 13.d(m,l)=d(m,l)+S(e).inc; 14.m.inc=S(e).inc; 15.Q.add(m);/* 将S(e)的直接祖先节点加入Q */ 16.endfor 17.endfor 18.closedQ.add(n); 19.endfor 20.gotoStep1; 本文的启发式路径规划过程基于预处理数据中的地标及其动态最短路径树,采用如下估价函数来指导搜索,使路径规划始终趋向于目标终点: (7) 上式中: f(n)为从起点s经由节点n到达终点t的距离估计; g(n)为从起点s到达节点n的实际距离,即为最短路径Dist(s,n)对应的路径值d(s,n); h(n)为从节点n到达终点t的预估距离,对于每个地标节点l∈L,根据三角不等式可知d(n,l)+d(l,n)≥d(l,t)且d(n,l)+d(t,l)≥d(n,l),遍历所有地标后将h(n)取值为最大值maxl∈L{d(l,t)-d(l,n),d(n,l)-d(t,l)}. 对于点对(s,t)的最短路径Dist(s,t),求解思想如下: 1) 如果起点s是地标节点,即s∈L,则根据以s.FSPT可求得Dist(s,t).如果目标点t是地标节点,即t∈L,则根据以t.TSPT可求得Dist(s,t).如果节点s、节点t在同一SPT中,且存在路径SPT(s,t),则由性质1可知SPT(s,t)即为Dist(s,t).如果以上条件均不满足,则转向步骤2,使用ALT算法求解Dist(s,t). 2) 将s加入队列closedQueue,并根据s的出度边集合O(s),将O(s)中各出度边e的终点D(e)加入openQueue,并计算其估价函数值f(D(e))和父节点P(D(e)). 3) 从openQueue中选取当前估价函数值最小的节点n,将n加入closedQueue,并从openQueue中移除n. 4) 依次遍历n的出度边集合O(n),若O(n)中出度边e的终点D(e)不存在于openQueue和closedQueue,则将D(e)加入openQueue,并根据式(7)计算其估价函数值f(D(e))和父节点P(D(e));若终点D(e)存在于openQueue,则根据式(7)计算当前估价函数值f′(D(e)),当f′(D(e)) 5) 重复步骤3和步骤4,直至目标节点t加入closedQueue或openQueue中没有新节点加入.若t存在于closedQueue,从节点t开始遍历各个节点的父节点,即可得到最短路径Dist(s,t);否则表明点对(s,t)不可达,即Dist(s,t)=φ. 根据上述算法思想,对于已获取地标集L及其动态最短路径树的图G,DALT算法的启发式路径规划查询执行过程描述如下: Algorithm4.-DALT算法的启发式路径规划 Step1. /*求解点对(s,t)的最短路径Dist(s,t) */ 1.ifs∈L 2.Dist(s,t) =s.FSPT(s,t); 3.print:Dist(s,t);/* 输出最短路径 */ 4.elseift∈L 5.Dist(s,t) =t.LSPT(s,t); 6.print:Dist(s,t); 7.elseif∃l.SPT(s,t) /*l∈L,l.SPT=l.FSPTorl.TSPT*/ 8.Dist(s,t) =t.SPT(s,t); 9.print:Dist(s,t); 10.else 23. closedQueue.add(s); 11.for∀e∈O(s) 12.f(D(e)) =g(D(e))+h(D(e)); 13.P(D(e)) =s; 14.openQueue.add(D(e)); 15.endfor 16.gotoStep2; 17.endif Step2. /* ALT算法 */ 1.whileopenQueue≠φ 2.n=minn{f(n)|n∈openQueue}; 3.openQueue.remove(n); 4.closedQueue.add(n); 5.ifn=t 6.endwhile 7.else 8.for∀e∈O(n) 9.ifD(e)∉openQueueandD(e)∉closedQueue 10.f(D(e)) =g(D(e))+h(D(e)); 11.P(D(e)) =n; 12.openQueue.add(D(e)); 13.elseifD(e)∈openQueue 14.f=g(D(e))+h(D(e)); 15.iff 16.f(D(e)) =f; 17.P(D(e)) =n; 18.openQueue.update(D(e)); 19.endif 20.endif 21.endfor 22.endif 23.endwhile 24.ift∈closedQueue 25.gotoStep3; 26.else 27. Dist(s,t) =φ; 28.endif Step3. /* 输出点对(s,t)的最短路径Dist(s,t) */ 1.whilet≠s 2.e= (P(t),t); 3.Dist(s,t).add(e); 4.t=P(t); 5.endwhile 6.print:Dist(s,t); 在预处理阶段,地标的SPT构造过程需要扫描点集合和边集合,与点的个数|V|和边的个数|E|相关,每个地标的SPT构造时间复杂度为O(|V|+|E|),因此路网的规模越大,构造过程所消耗的时间便越大.SPT保存了地标与各节点之间的最短路径,存储空间与节点数|V|和最短路径树规模|SPT|相关,其中|SPT|即为(|V|-1),因此路网的点集合越大,所占用的存储空间也越多. 在SPT动态更新阶段,设SPT中受权值变化影响的节点数为t,与这t个受影响节点有连接关系的边数为Et,更新过程中节点的增量更新次数为tr,更新节点的父节点或子节点的次数为tp,显然tp≤tr≤t.文献[12]提出的DSPT算法在更新SPT时,首先将受影响的节点加入队列中并设置初始增量值,然后扫描与这些节点有连接关系的边,同时计算队列中节点的最小增量并以此判断该节点及其子孙节点或祖先节点是否需要更新,最后再次扫描队列中的节点依次更新权值及其父节点或子节点,时间复杂度为O(Et+tp×tr).DALT算法采用了自上而下的方式计算队列中所有节点的最小增量并同步更新节点,避免了DSPT算法中对节点和边的重复扫描及更新操作,时间复杂度为O(Et+t).因此与DSPT算法相比,受影响的节点越多,DALT算法的更新策略更具优越性. 在路径规划阶段,Dijkstra算法、A*算法的时间复杂度分别为O(|V|×|V|)和O(|V|+|E|),ALT算法基于A*算法,时间复杂度也为O(|V|+|E|).DALT算法改进了ALT算法,在预处理阶段所构造的SPT从一定程度上降低了路径规划阶段的扫描需求,对于符合特定条件的路径规划,只需根据预处理数据直接输入最短路径即可,时间复杂度介于O(1)和O(|V|+|E|)之间.因此在规模越大、查询越频繁的路径规划中可获得比ALT算法更好的时间效率. 本文的实验在INTEL Core i7-4790 CPU 3.60 GHz、8GB RAM台式机上完成,实验数据选用OpenStreetMap开源地图平台提供的城市路网数据,各个路网数据的简称、节点数、边数和数据大小如表1所示(以路网规模大小升序排列). 本文的实验包括:静态路径规划实验(实验1和实验2)和动态网络更新实验(实验3和实验4).在路径规划过程中,最短路径的度量标准为路径的累加权值最小,初始状态下各路段的权值为其欧氏距离.在动态网络更新实验中,随机变化部分边的权值(以一定比率增加或减小),模拟路线规划过程中路况的动态变化. 表1 路网数据表Table 1 Road networks 对于每个路网数据的实验,均使用随机方式选取16个地标,ALT算法和DALT算法采用相同的地标集.由于实验结果跨度较大,为获得较好的视觉对比效果,图2-图3和图5-图7的纵坐标使用以10为基数的对数刻度,图4-图7的横坐标使用以10为基数的对数刻度. 实验内容:分别使用ALT算法和DALT 算法完成对BJ、SEL、TYO和PAR四个路网数据的预处理模块,并比较两种算法的预处理时间费用和预处理数据额外占用空间费用. 表2 静态路径规划实验结果表Table 2 Experiment result of static path planning 实验结果:如表2所示,将四个路网的静态路径规划实验结果数据汇总可得,ALT算法和DALT算法中每个节点的额外占用空间分别为74字节和91字节,DALT算法每节点的额外空间费用虽然比ALT算法增加了22.97%,但总体的预处理时间费用只增加了6.28%.如图1所示,对比四个路网在预处理数据占用空间,其中DALT算法高于ALT算法的部分,即为DALT算法中用于存储地标SPT的费用,且该费用随着路网规模的增大而增多. 图1 预处理数据占用空间Fig.1 Space of preprocessing data 实验内容:分别使用Dijkstra算法、A*算法、ALT算法和DALT 算法完成对BJ、SEL、TYO和PAR四个路网数据的最短路径查询模块.对于每个路网,随机选取20组点对(s,t)后进行1000次路径规划. 图2 实验2的平均查询时间Fig.2 Average query time of experiment 2 实验结果:对比图2中各算法的平均查询时间和图3中的平均扫描次数,发现路径规划所消耗的时间与扫描次数成正比关系.此外,通过表2可知,DALT算法的总体查询时间比ALT算法减少了51.06%,同时搜索过程中对节点和边的扫描次数减少了46.59%,证明在规模越大、距离越长的路径规划中,扫描次数较少的DALT算法可以获得比ALT算法更好的时间效率. 图3 实验2的平均扫描次数Fig.3 Average number of scans of experiment 2 实验内容:分别使用DSPT算法和DALT 算法更新地标的SPT.对于每个路网,首先从实验2所求得的最短路径中随机选取10条连边e,然后进行实验3-a和实验3-b.实验3-a将每条边e的权值增加1倍后更新受影响的SPT;实验3-b将其权值减小到原值后,再次更新受影响的SPT. 图4 实验3-a的平均更新时间Fig.4 Average query time of experiment 3-a 实验结果:在实验3-a中,如图4和图5所示,当权值增加时,DSPT算法与DALT算法的平均更新时间和平均更新次数比较接近,当受影响的节点数较小时,DALT算法的平均更新次数较少.在实验3-b中,如图6和图7所示,当权值减小时,DALT算法比DSPT算法的平均更新时间和平均扫描次数明显更可观,且受影响的节点数越大,两者的差距越大. 根据表3,与DSPT算法相比,DALT算法的总体更新时间及其扫描次数分别减小了51.16%和52.32%.其中权值增加实验中,DALT算法的更新时间及其扫描次数分别减小了3.82%和5.39%;权值减小实验中,DALT算法的更新时间及其扫描次数则分别减小了98.49%和99.26%,表明当权值减小时,DALT算法的更新效率更加显著. 图5 实验3-a的平均扫描次数Fig.5 Average number of scans of experiment 3-a 图6 实验3-b的平均更新时间Fig.6 Average query time of experiment 3-b 图7 实验3-b的平均扫描次数Fig.7 Average number of scans of experiment 3-b 表3 动态网络更新实验结果表Table 3 Experiment result of dynamic updating 这是因为权值增加时,队列中受影响的节点即为变化边节点的子孙节点或祖先节点;而权值减小时,队列中除了变化边节点的子孙节点或祖先节点外,在更新过程中还会计算并加入新的受影响的节点及其子孙节点或祖先节点,比权值增加的更新过程更为复杂,因此在更新效率方面避免了大量冗余计算的DALT算法明显优于DSPT算法. 实验内容:在实验3的基础上,在TYO路网中对选取边的权值分别增加0.25倍、0.5倍和1倍,然后使用ALT算法和DALT算法执行实验2中TYO路网对应的路径规划实验,以此模拟两种算法在轻度拥堵、中度拥堵和重度拥堵的不同路况下网络更新后的查询效率对比,并将实验2中的实验结果视为正常状态下的查询效率. 实验结果:在不同路况下,如表4所示,从平均查询时间和平均扫描次数两个方面进行对比,发现DALT算法的查询效率明显优于ALT算法.依次将四列实验数据使用线性回归拟合后,得到ALT算法和DALT算法的平均查询时间的直线斜率分别为236.6和168.1,平均扫描次数的直线斜率分别为166.6和105.6. 表4 TYO路网不同路况下的实验结果表Table 4 Experiment result of path planning in different conditions of TYO road networks 从几何角度而言,线性斜率的绝对值越大,则表示其对应的直线越倾斜,即因变量的变化趋势越明显.由此可知,在不同路况的模拟实验中,随着拥堵现象的加重,在查询时间和扫描次数方面,DALT算法比ALT算法拥有更小的变化趋势和更好的查询效率,体现了DALT算法的鲁棒性与高效性. 为解决时变公路网络中的最短路径规划问题,本文结合地标导向的预处理技术和最短路径树的特性提出了DALT算法.实验证明在时变路网的动态应用场景中,DALT算法不仅具有鲁棒性和准确性,而且拥有较低的计算复杂度,与ALT算法相比,查询时间及其扫描次数分别减少了51.06%和46.59%;与DSPT算法相比,更新时间及其扫描次数分别减少了51.16%和52.32%.DALT算法以牺牲存储空间的方式,提高了算法的路径规划效率和路网动态更新效率,下一步将对算法中动态最短路径树的占用空间优化进行相应研究. : [1] Dijkstra E W.A note on two problems in connexion with graphs[J].Numerische Mathematik,1959,1(1):269-271. [2] Delling D,Sanders P,Schultes D,et al.Engineering route planning algorithms[C].Proceedings of Algorithmics of Large and Complex Network,2009:117-139. [3] Bast H,Delling D,Goldberg A V,et al.Route planning in transportation networks[R].MSR-TR-2014-04,Redmond:Microsoft Corporation,2014. [4] Hart P E,Nilsson N J,Raphael B.A formal basis for the heuristic determination of minimum cost paths[J].IEEE Transactions on Systems Science and Cybernetics,1968,4(2):100-107. [5] Goldberg A V,Harrelson C.Computing the shortest path:A* search meets graph theory[R].MSR-TR-2004-24,Redmond:Microsoft Corporation,2004. [6] Gutman R J.Reach-based routing:a new approach to shortest path algorithms optimized for road networks[C].Proceedings of the 6th Workshop on Algorithm Engineering and Experiments,2004:100-111. [7] Nannicini G,Delling D,Liberti L,et al.Bidirectional A* search for time-dependent fast paths[C].Proceedings of International Workshop on Experimental and Efficient Algorithms,2008:334-346. [8] Geisberger R,Sanders P,Schultes D,et al.Contraction hierarchies:faster and simpler hierarchical routing in road networks[C].Proceedings of International Workshop on Experimental and Efficient Algorithms,2008:319-333. [9] Song Q,Wang X.Efficient routing on large road networks using hierarchical communities[J].IEEE Transactions on Intelligent Transportation Systems,2011,12(1):132-140. [10] Bauer R,Delling D,Sanders P,et al.Combining hierarchical and goal-directed speed-up techniques for Dijkstra′s algorithm[J].ACM Journal of Experimental Algorithmics,2010,15(2.3):1-31. [11] Narvaez P,Siu K Y,Tzeng H Y.New dynamic algorithms for shortest path tree computation[J].IEEE/ACM Transactions on Networking,2000,8(6):734-746. [12] Xiao B,Cao J,Shao Z,et al.An efficient algorithm for dynamic shortest path tree update in network routing[J].Journal of Communications and Networks,2007,9(4):499-510. [13] Kaufman D E,Smith R L.Fastest paths in time-dependent networks for intelligent vehicle-highway systems applications[J].Journal of Intelligent Vehicle Highway Systems,1993,1(1):1-11. [14] Delling D,Wagner D.Landmark-based routing in dynamic graphs[C].Proceedings of International Conference on Experimental Algorithms,2007:52-65. [15] Ran Chun-feng.Research on algorithm for detecting shortest path in mobile intelligence platform-based navigation systems and its application[D].Beijing:Capital Normal University,2013. [16] Kim J,Han W S,Oh J,et al.Processing time-dependent shortest path queries without pre-computed speed information on road networks[J].Information Sciences,2014,255(1):135-154. [17] Huang W,Yan C,Wang J,et al.A time-delay neural network for solving time-dependent shortest path problem[J].Neural Networks,2017,90(1):21-28. [18] Xiao B,Cao J,Zhuge Q,et al.Dynamic shortest path tree update for multiple link state decrements[C].Proceedings of IEEE Global Telecommunications Conference,2004:1163-1167. [19] Dreyfus S E.An appraisal of some shortest-path algorithms[J].Operations Research,1968,17(3):395-412. [20] Tan Guo-zhen,Gao Wen.Shortest path algorithm in time-dependent networks[J].Chinese Journal of Computers,2002,25(2):165-172. [21] Lin Lan,Yan Chun-gang,Jiang Chang-jun,et al.Complexity and approximate algorithm of shortest paths in dynamic networks[J].Computer Engineering and Science,2007,30(4):608-614. [22] Meng Ke,Zhang Chun-yan.Landmark-oriented heuristic routing algorithm in traffic network[J].Journal of Computer Applications,2012,32(4):1053-1055. 附中文参考文献: [15] 冉春风.移动智能终端导航系统中最短路径算法的研究与应用[D].北京:首都师范大学,2013. [20] 谭国真,高 文.时间依赖的网络中最小时间路径算法[J].计算机学报,2002,25(2):165-172. [21] 林 澜,闫春钢,蒋昌俊,等.动态网络最短路问题的复杂性与近似算法[J].计算机学报,2007,30(4):608-614. [22] 孟 珂,张春艳.地标导向的启发式路径规划算法[J].计算机应用,2012,32(4):1053-1055.4.2 基于预处理数据的启发式路径规划查询
4.3 算法分析
5 实 验
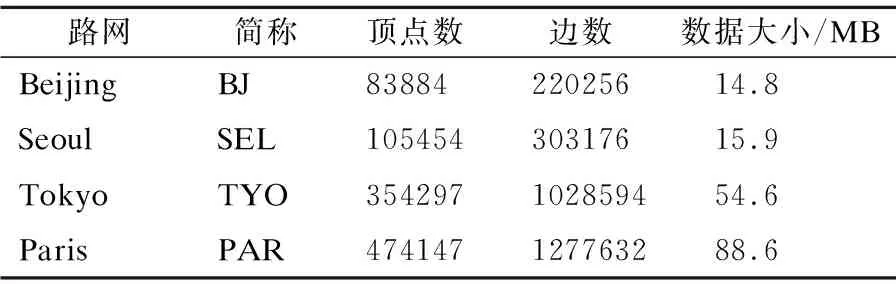
5.1 实验1


5.2 实验2
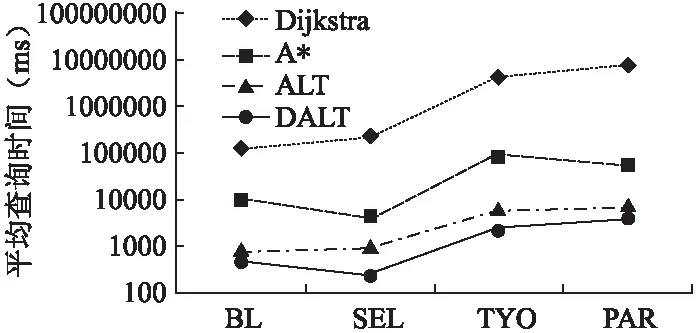
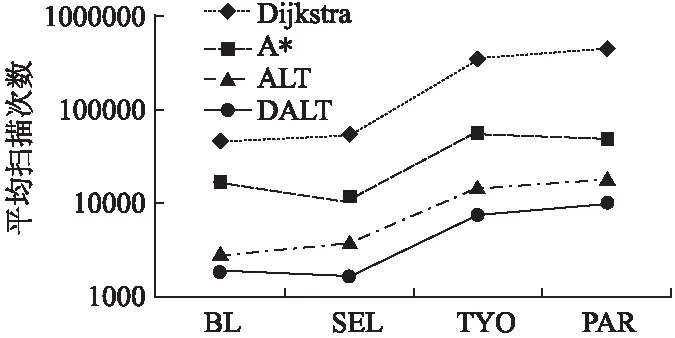
5.3 实验3
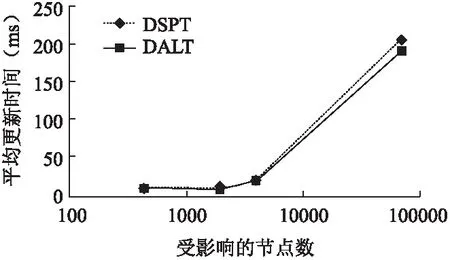
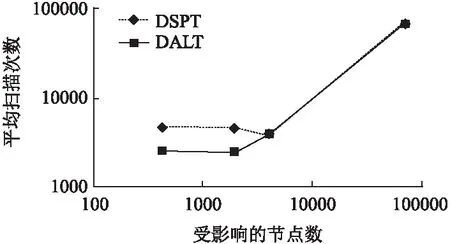
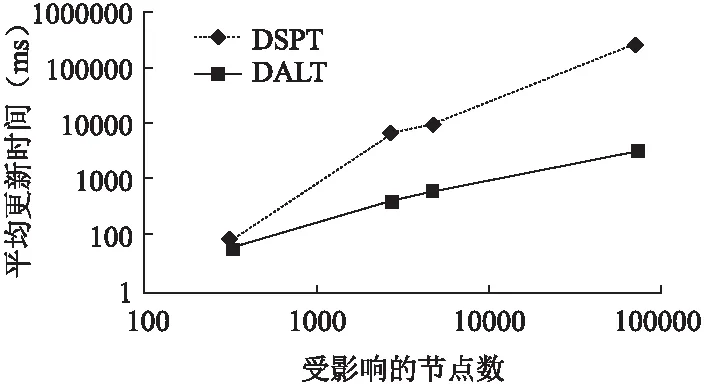
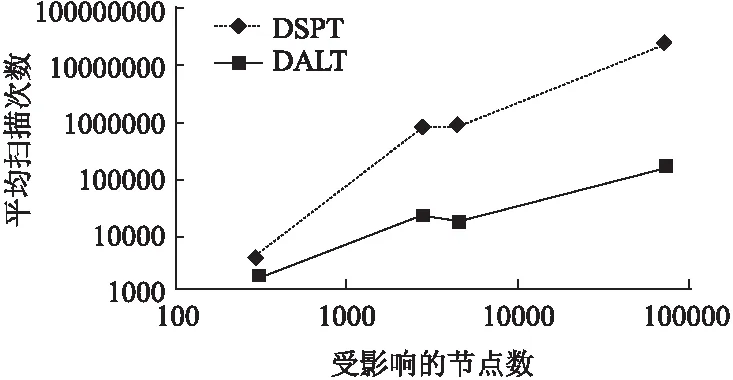

5.4 实验4

6 结 论

