用模糊积分集成重复训练极限学习机的数据分类方法
翟俊海,张素芳,周昭一
1(河北大学 数学与信息科学学院 河北省机器学习与计算智能重点实验室 , 河北 保定 071002)
2(中国气象局气象干部培训学院河北分院, 河北 保定 071000)
1 引 言

由于ELM具有学习速度快,泛化能力强的特点,所以引起了机器学习和数据挖掘领域研究人员的广泛关注,已成为这两个领域的研究热点.从模型的角度,ELM是针对单隐含层前馈神经网络训练而提出的算法,近几年随着深度学习的盛行,研究人员将深度学习的思想引入到了ELM中,提出了多层ELM[4]、局部感受域ELM[5]和深度ELM[6].将深度学习和ELM相结合最早出现在文献[6]中,其主要贡献是提出了ELM自动编码器(ELM autoencoder,ELM-AE).其他的深度ELM模型大多都是在ELM-AE的基础上提出的.例如,Tissera等人[7]通过约束感受域机制选择无训练的输入权,提出了一种改进的ELM-AE.基于表示学习[8],Ding等人[9]提出了一种无监督极限学习机.Zhou等人[10]通过将一个大的ELM网络划分成多个子ELM网络,提出了堆叠ELM.
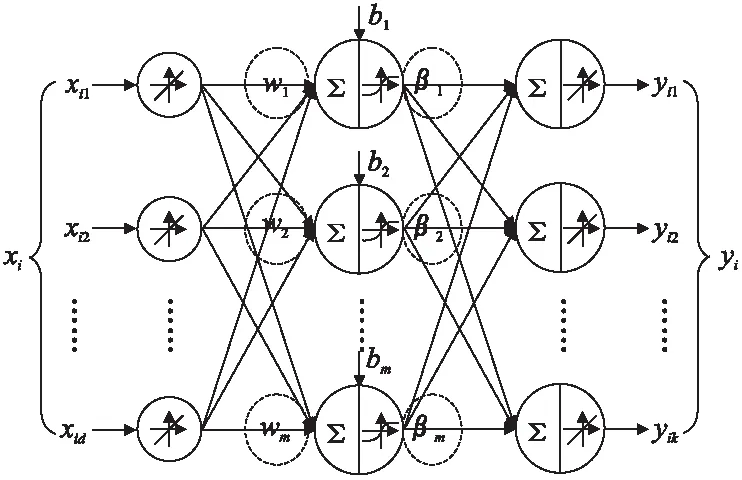
图1 具有特殊结构的单隐含层前馈神经网络Fig.1 Single-hidden layer need-forward neural networks with special structure
众所周知,利用大数据训练深度学习模型,可提高深度学习模型的泛化能力[11].最近几年,从事ELM研究的人员研究了大数据ELM的训练问题,或将ELM应用到大数据处理中.例如,He等人[12]提出了并行ELM(Parallel ELM,PELM),并应用于求解大数据回归问题,取得了良好的效果.在PELM的基础上,Xin等人[13]通过将PELM中的两阶段MapReduce替换为单阶段MapReduce,提出了分布式ELM(Distributed ELM,DELM),取得了比PELM更好的泛化性能.针对非平衡大数据分类问题,基于MapReduce和集成ELM,Zhai等人[14]提出了一种有效的非平衡大数据分类方法.针对大数据应用,Akusok等人[15]开发了一套高性能的ELM工具箱.焦李成等人[16]对近七十多年神经网络研究,包括深度网络研究,进行了全面深入的综述,具有很高的参考价值.
在ELM中,网络结构选择问题就是确定隐含层最优结点个数问题.关于这个问题,研究人员提出了一系列的解决方法.例如,Huang等人[17]提出了I-ELM (Incremental ELM),I-ELM用逐个增加隐含层结点的方法确定最优网络结构,直到满足预定义的停止条件.在I-ELM中,当一个新的隐含层结点加入到网络后,已经存在的输出层权值保持不变.Feng等人[18]提出了EM-ELM (Error Minimized-ELM).与I-ELM不同,当一个新的隐含层结点加入到网络后,所有的输出层权值(包括已经存在的)都要更新.与I-ELM相比,EM-ELM具有更好的泛化性能,但是计算复杂度比I-ELM的高.基于信息判据理论,Rong等人[19]提出了P-ELM (Pruned-ELM).P-ELM以2统计量和信息增益作为启发式度量隐含层结点的重要性,将不重要的隐含层结点去掉,保留重要的隐含层结点.用该方法处理连续值数据集时,需要对连续值属性进行离散化,这会导致信息丢失及高计算复杂度.针对这一问题,基于相容粗糙集理论,Zhai等人提出了两种改进的方法[20,21],可解决上述问题.基于多响应稀疏回归技术,Miche等人[22]提出了OP-ELM (Optimally Pruned-ELM).这些ELM网络结构选择方法的共性问题是计算复杂度高,其原因要么是由于迭代计算Moore-Penrose广义逆矩阵,要么是由于迭代计算度量隐含层结点重要性的启发式.用极限学习机重复训练单隐含层前馈神经网络可得到不同的网络模型.受极限学习机这一特点的启发,提出了一种用模糊积分集成重复训练极限学习机的数据分类方法.提出的方法具有2个优点:1)网络模型具有良好的多样性;2)具有良好的泛化能力.
2 基础知识
本节简要介绍将要用到的基础知识,包括极限学习机[1,2]和模糊积分[23,24].
2.1 极限学习机(Extreme Learning Machine,ELM)
ELM[1,2]是一种简单高效的训练具有特殊结构单隐含层前馈神经网络的随机化算法.给定一个包含n个样例的训练集Tr={(xi,yi)|xi∈Rd,yi∈Rk},设SLFNs的输入层、隐含层和输出层结点的个数分别是d、m和k,SLFNs的结构可用一个三元组(d,m,k)来表示.具有结构(d,m,k)的SLFNs(如图1所示)可用下面的公式表示.
(1)
在公式(1)中,wj和bj分别是随机生成的输入层权和隐含层结点偏置,βj是输出层权.
对于训练集Tr中的每一个样例xi(1≤i≤n),令SLFNs的实际输出f(xi)等于期望输出yi(1≤i≤n),得到下面的公式(2).
(2)
公式(2)的矩阵表示形式为:
Hβ=Y
(3)
其中,
(4)
(5)
(6)
对于线性系统(3),如果SLFNs的隐含层结点个数m等于训练集Tr中的样例数n,那么矩阵H是方阵,而且可逆.此时,用线性系统(3)可以以零误差逼近训练集Tr中的每一个样例.但是,一般情况下,样例数n远远大于隐含层结点数m.此时,难于得到(3)的精确解,但是可用下面优化问题的解来逼近.

(7)
上述优化问题的解由下面的公式给出
(8)
其中,H+=(HHT)-1H是H的Moore-Penrose广义逆矩阵.
图2给出了ELM算法的伪代码.

图2 ELM算法的伪代码Fig.2 Pseudo code of ELM algorithm
用模糊积分集成基本分类器时,基本分类器的输出必须是后验概率.在本文中,我们用下面的软最大化函数将SLFNs的输出变换到[0,1]区间,变换后的结果可看作后验概率的近似.
(9)
2.2 模糊积分
模糊积分[23,24]是一种非线性积分,可应用于分类器集成.因为模糊积分能很好地刻画基本分类器之间的交互作用,所以与其他分类器集成工具相比,用模糊积分进行分类器集成能获得更好的分类性能.下面介绍模糊积分理论中相关的基本概念,包括决策矩阵、模糊测度、Choquet积分等.
给定训练集Tr={(xi,yi)|xi∈Rd,yi∈Rk}和测试集Te={(xi,yi)|xi∈Rd,yi∈Rk},Ω={ω1,ω2,…,ωk}是类标的集合,C={C1,C2,…,Cl}是从Tr训练出的l个分类器集合,Ci(1≤i≤l)称为元分类器或基本分类器.对于任意的x∈Te和任意的Ci∈C,有
Ci(x)=(μi1(x),μi2(x),…,μik(x))
其中,μij(x)∈[0,1](1≤i≤l;1≤j≤k)表示分类器Ci将样例x分类为第j类的隶属度.
定义1. 给定C={C1,C2,…,Cl},Ω={ω1,ω1,…,ωk}和Te.对于任意的x∈Te,称下面的矩阵为决策矩阵.
(10)
矩阵DM(x)的第i行表示分类器Ci将样例x分类为各个类的隶属度,矩阵DM(x)的第j列表示不同的分类器将测试样例x分类为第j类的隶属度.
定义2. 给定C={C1,C2,…,Cl},设P(C)是C的幂集,定义在C上的模糊测度是一个集函数:g:P(C)→[0,1],它满足如下条件:
1)g(Ø)=0,g(C)=1;
2) ∀A,B⊆C,若A⊂B,则g(A)≤g(B).
如果∀A,B⊆C,A∩B=Ø,下式成立,则称g为λ模糊测度.
g(A∪B)=g(A)+g(B)+λg(A)g(B)
(11)
其中,λ>-1,且λ≠0,它的值可由下式确定.
(12)
其中,gi表示在单个分类器上的模糊测定,即下面定义3中的模糊密度.
定义3. 给定C={C1,C2,…,Cl},∀Ci(1≤i≤l),令gi=g({Ci}),gi称为分类器Ci的模糊密度,gi通常用下面的公式(13)确定.
(13)
其中,pi是分类器Ci在验证集或测试集上的性能指标(如验证精度或测试精度).所以,一旦训练出l个基本分类器,那么它们的模糊密度即可得到.
定义4. 给定C={C1,C2,…,Cl},g是C上的模糊测度,函数h:C→R+关于g的Choquet积分定义为:
(14)
其中,0≤h(C1)≤h(C2)≤…≤h(Cl)≤1,h(C0)=0,Ai⊆C,Ai={C1,C2,…,Ci},g(A0)=0.
3 用模糊积分集成重复训练极限学习机的数据分类方法
本节介绍用模糊积分集成重复训练极限学习机的数据分类方法.首先介绍提出的方法的基本思想,然后介绍选择模糊积分作为分类器集成工具的理由,最后给出算法的伪代码.
用极限学习机训练单隐含层前馈神经网络时,由于输入层权值和隐含层结点的偏置是随机生成的,这样重复训练会得到不同的网络模型.不同的网络模型之间的差异表现为参数不同,网络结构是相同的,即隐含层结点的个数是相同的.如果隐含层结点个数也随机确定,那么重复训练会得到参数不同结构也不同的网络模型,这些网络模型具有较大的差异,具有良好的多样性.受极限学习机这一特点的启发,提出了用模糊积分集成重复训练极限学习机的数据分类方法.提出的方法包括3步:
第1步.用极限学习机重复训练单隐含层前馈神经网络.具体地,首先用随机化方法生成一个区间[pd,qd]中的随机整数m,m即为隐含层结点的个数.其中,d为数据集的维数,p和q是大于1的正整数.单隐含层前馈神经网络的结构确定后,用ELM算法重复训练l个基本分类器SLFNs.
第2步.用软最大化函数(9)将SLFNs的输出变换到[0, 1]区间,使得SLFNs的输出是一个后验概率分布.
第3步.用模糊积分集成训练好的基本分类器SLFNs,并用于数据分类.
提出的算法的伪代码如图3所示.
下面介绍选择模糊积分作为分类器集成工具的理由.
在分类器集成的一般框架中,有一种默认的假设:基本分类器之间是相互独立的,或者说基本分类器之间没有交互作用。但是,在许多实际问题中,这个假设是不成立的。实际上,在基本分类器之间存在内在的交互作用。这种交互作用可能是正交互,正交互可使基本分类器之间相互协作,共同提高。这样集成系统能充分发挥基本分类器的优势,克服彼此的不足,最终获得比任何一个单个基本分类器更好的分类性能。交互作用也可能是负交互,负交互使基本分类器之间相互抑制,集成具有负交互作用的基本分类器,不仅不能提高集成系统的分类性能,还会降低分类性能。模糊积分能很好地刻画基本分类器之间的交互作用,这也是我们选择模糊积分作为集成工具的理由。
4 实验结果及分析
为了描述方便,用FI-ELM表示提出的算法。若算法中的SLFNs采用固定结构,集成采用简单的多数投票法,则相应的算法用MV-ELM表示.为了验证本文方法FI-ELM的有效性,我们设计了两个实验:1)与ELM和MV-ELM在分类精度上进行了比较;2)实验结果的统计分析.为了比较的公平性,在相同的实验环境、相同的参数设置和相同的数据集上进行实验比较.实验环境是Intel(R) Core(TM) i5-3210M 2.50GHz CPU,4GB内存,Windows 10操作系统,Matlab R2013a软件平台.实验所用的数据集及参数设置如表1所示.
算法2.用模糊积分集成重复训练极限学习机的数据分类算法

图3 提出的算法的伪代码Fig.3 Pseudo code of the proposed algorithm
1)与ELM和MV-ELM在分类精度上的比较
在这个实验中,ELM和MV-ELM中单隐含层前馈神经网络隐含层结点的个数用文献[25]中的方法确定,对于不同的数据集,隐含层结点的个数设置为不同的值,具体设置如表2所示.网络结构确定后,用[-1, +1]区间服从均匀分布的随机数初始输入层权值和隐含层偏置.在ELM中,用ELM算法训练一个单隐含层前馈神经网络,并用于数据分类.在MV-ELM中,用ELM算法重复训练5个单隐含层前馈神经网络,用多数投票法进行集成,并用于数据分类.
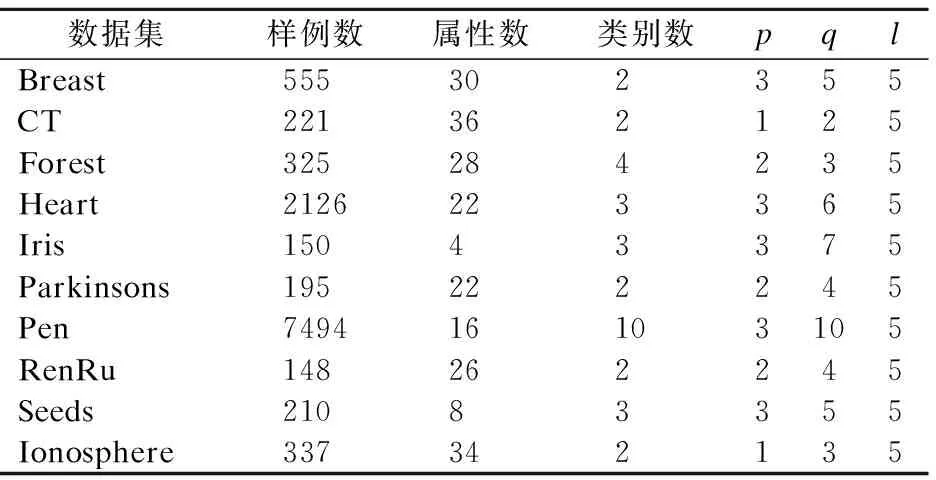
表1 实验所用的10个数据集的基本信息及参数设置Table 1 Basic information of 10 data sets used in the experiments and the configuration of parameters
在本文方法FI-ELM中,单隐含层前馈神经网络隐含层结点的个数也随机生成.具体地,在每一次重复训练单隐含层前馈神经网络时,首先用区间[pd,qd]中随机生成的正整数m作为隐含层结点的个数.然后用ELM算法训练结构为(d,m,k)的单隐含层前馈神经网络,最后用模糊积分进行集成,并用于数据分类.与ELM和MV-ELM中的方法在分类精度上比较的实验结果列于表3中,从列于表3的实验结果可以看出,本文方法FI-ELM在10个数据集上的均优于ELM和MV-ELM.

表2 ELM和MV-ELM中SLFNs隐含层结点个数的设置Table 2 Selected number of hidden nodes of SLFNs in ELM and MV-ELM
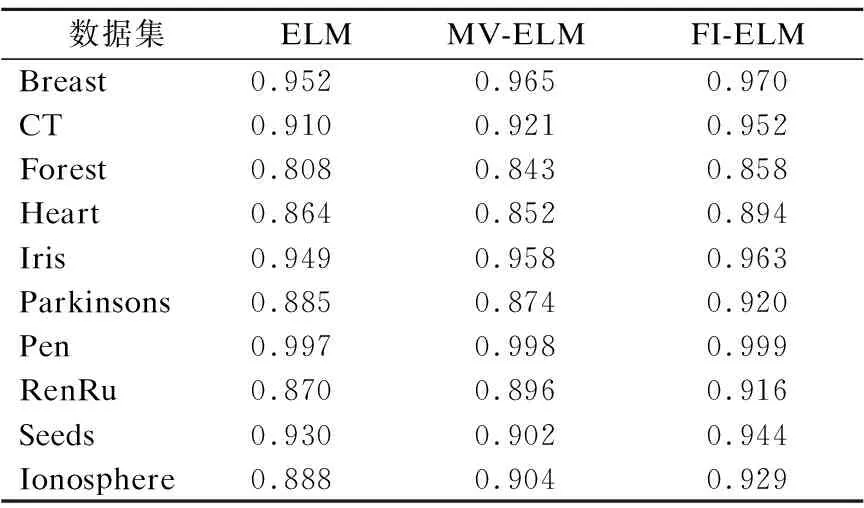
表3 与ELM和MV-ELM在分类精度上的比较Table 3 Comparisons on classification accuracy with ELM and MV-ELM
2)实验结果的统计分析
为了从统计意义上证明本文方法FI-ELM的有效性,我们用成对T-检验对实验结果进行了统计分成.T-检验中的显著性水平设置为0.05,对三种方法分别构造关于分类精度的10维统计量,然后用MATLAB函数ttest2(X, Y)进行成对T-检验的统计分析,结果在表4中给出.在表4中,第2列(P-值1)是本文方法FI-ELM与ELM实验结果的统计分析结果;

表4 对实验结果的统计分析Table 4 Statistical analysis on experimental results
第3列(P-值2)是本文方法FI-ELM与MV-ELM实验结果的统计分析结果.从列于表3的P-值可以看出,从统计意义上说,本文方法FI-ELM在10个数据集上的分类性能均优于ELM和MV-ELM的分类性能,这一结论以0.95的概率成立.因此,上述结论具有可信性.
5 结 论
本文提出了一种用模糊积分集成重复训练极限学习机的数据分类方法.利用该方法解决实际问题,可以避免网络结构选择问题.另外,与传统的ELM和MV-ELM相比,本文提出的方法具有更好的分类性能.我们认为本文提出的方法在分类性能上优于ELM和MV-ELM的原因有以下3点:
1)作为分类器集成工具,模糊积分能够很好地对基本分类器之间的交互作用进行建模,各个基本分类器之间能够取长补短;
2)对于给定的数据集,隐含层结点的个数由一个区间内随机整数随机确定,这样重复训练的网络具有不同的结构(结构相同的概率非常小),从而基本分类器具有良好的多样性;
3)对于每一个基本分类器,它用整个训练集进行训练,而不是用训练集的子集进行训练,这样训练集中的每一个样例,对于每一个基本分类器都是可见的.
:
[1] Huang G B,Zhu Q Y,Siew C K.Extreme learning machine:a new learning scheme of feedforward neural networks [C].IEEE International Joint Conference on Neural Networks (IJCNN2004),Budapest,Hungary,2004.
[2] Huang G B,Zhu Q Y,Siew C K.Extreme learning machine:theory and applications [J].Neuro Computing,2006,70(1-3):489-501.
[3] Huang G B,Wang D H,Lan L.Extreme learning machines:a survey [J].International Journal of Machine Learning and Cybernetics,2011,2(2):107-122.
[4] Tang J,Deng C,Huang G B.Extreme learning machine for multilayer perceptron [J].IEEE Transactions on Neural Networks and Learning Systems,2016,27(4):809-821.
[5] Huang G B,Bai Z,Chi M V.Local receptive fields based extreme learning machine [J].IEEE Computational Intelligence Magazine,2015,10(2):18-29.
[6] Kasun L L C,Zhou H,Huang G B,et al.Representational learning with ELMs for big data [J].IEEE Intelligent Systems,2013,28(6):31-34.
[7] Tissera M D,Mcdonnell M D.Deep extreme learning machines:supervised autoencoding architecture for classification [J].Neuro Computing,2016,174(Part A):42-49.
[8] Bengio Y,Courville A,Vincent P.Representation learning:a review and new perspectives [J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2013,35(8):1798-1828.
[9] Ding S F,Zhang N,Zhang J.Unsupervised extreme learning machine with representational features [J].International Journal of Machine Learning and Cybernetics,2017,8(2):587-595.
[10] Zhou H,Huang G B,Lin Z,et al.Stacked extreme learning machines [J].IEEE Transactions on Cybernetics,2015,45(9):2013-2024.
[11] Chen X W,Lin X.Big data deep learning:challenges and perspectives [J].IEEE Access,2014,2:514-525.
[12] He Q,Shang T F,Zhuang F Z,et al.Parallel extreme learning machine for regression based on MapReduce [J].Neurocomputing,2013,102:52-58.
[13] Xin J C,Wang Z Q,Chen C,et al.ELM:distributed extreme learning machine with MapReduce [J].World Wide Web,2014,17(5):1189-1204.
[14] Zhai J H,Zhang S F,Wang C X.The classification of imbalanced large data sets based on MapReduce and ensemble of ELM classifiers [J].International Journal of Machine Learning and Cybernetics,2017,8(3):1009-1017.
[15] Akusok A,Bjork K M,Miche Y,et al.High-performance extreme learning machines:a complete toolbox for big data applications [J].IEEE Access,2015,3:1011-1025.
[16] Jiao Li-cheng,Yang Shu-yuan,Liu Fang,et al.Seventy years beyond neural networks:retropect and prospect [J].Chinese Journal of Computers,2016,39(8):1697-1716.
[17] Huang G B,Chen L,Siew C K.Universal approximation using incremental constructive feedforward networks with random hidden nodes [J].IEEE Transactions on Neural Networks,2006,17(4):879-892.
[18] Feng G R,Huang G B,Lin Q P,et al.Error minimized extreme learning machine with growth of hidden nodes and incremental learning [J].IEEE Transactions on Neural Networks,2009 20(8):1352-1357.
[19] Rong H J,Oon Y S,Tan A H,et al.A fast pruned-extreme learning machine for classification problem [J].Neurocomputing,2008,72(1-3):359-366.
[20] Zhai J H,Shao Q Y,Wang X Z.Improvements for P-ELM1 and P-ELM2 pruning algorithms in extreme learning machines [J].International Journal of Uncertainty,Fuzziness and Knowledge-Based Systems,2016,24(3):327-345.
[21] Zhai J H,Shao Q Y,Wang X Z.Architecture selection of elm networks based on sensitivity of hidden nodes [J].Neural Processing Letters,2016,44(2):471-489.
[22] Miche Y,Sorjamaa A,Bas P,et al.OP-ELM:optimally pruned extreme learning [J].IEEE Transactions on Neural Networks,2010,21(1):158-162.
[23] Ralescu D,Adams G.The fuzzy integral [J].Journal of Mathematical Analysis and Applications,1980,75(2):562-570.
[24] Abdallah A C B,Frigui H,Gader P.Adaptive local fusion with fuzzy integrals [J].IEEE Transactions on Fuzzy Systems,2012,20(5):849-864.
[25] Zhai Jun-hai,Li Ta,Zhai Meng-yao,et al.Experimental research on random mapping function in ELM [J].Computer Engineering,2012,38(20):164-168.
附中文参考文献:
[16] 焦李成,杨淑媛,刘 芳,等.神经网络七十年:回顾与展望[J].计算机学报,2016,39(8):1697-1716.
[25] 翟俊海,李 塔,翟梦尧,等ELM中随机映射作用的实验研究[J].计算机工程,2012,38(20):164-168.

