一种面向不平衡数据流的集成分类算法
孙艳歌,王志海,白 洋
1(信阳师范学院 计算机与信息技术学院,河南 信阳 464000)
2(北京交通大学 计算机与信息技术学院,北京 100044)
1 引 言
随着信息技术的快速发展,在诸如无线传感器网络、实时交通系统、网络流量监测和信用卡欺诈检测等诸多应用领域中产生了高速动态、数据规模宏大且连续不断的数据流(Data Streams)[1].这些数据中蕴含着丰富的信息亟待我们去挖掘.
与传统的静态数据有所不同,数据流具有快速、实时、无限、单遍、且蕴含的概念会发生变化的特性.在真实的数据流环境中,数据是随着时间不断变化的[2,3],因此数据所蕴含的概念会随着时间而发生改变,即发生概念漂移(Concept Drift)[4,5].例如:顾客网上购物偏好随个人兴趣、商家信誉、服务类型等因素的变化而改变;天气预报可能会随着季节变化而发生改变.概念漂移会使得原有的分类模型不再适应新的数据,这就需要快速的检测到这种变化,并动态更新模型以适应这种改变[6-8].
文献[6]将传统的概念漂移处理方法划分为:基于实例选择,基于实例加权与集成学习三种方法.其中,集成学习方法是最广泛使用的用于处理概念漂移的方法[7].然而,已有的数据流分类算法都是基于数据流类分布是大致平衡这一假设的,然而在现实世界中存在着大量的类分布不均衡数据.如信用卡的欺诈辨识、网络入侵检测、在线实时医疗诊断等诸多应用中人们往往更关注对于少数类的分类情况.
在机器学习领域中,研究者对不平衡学习分类问题进行了大量的研究[9-13].主要集中在以下3个方面:一是通过调整不同类别样本的权重来重构训练集,但是有可能会丢失一部分样本信息[9,10];二是在改进传统的算法的基础上设计代价敏感的分类算法[11,12];三是采用集成学习技术[13].由于数据流的连续、快速、无限和多变等特点,使得以上方法不能直接应用于数据流环境中.
本文提出了一种基于集成学习的不平衡数据流分类算法.主要贡献如下:
1)针对数据流中的概念漂移问题,采用基于数据块的集成方式,利用周期更新分类器权重来应对概念漂移.
2)针对数据流中的类不平衡问题,首先利用过采样技术增加正类样本的比例,再利用欠采样技术来删除负类样本,从而达到平衡各类样本的目的.
3)在提高集成分类效果方面,在分类器权重更新过程中综合考虑了分类器在最新数据块上的分类正确率和分类错误的代价,同时,在分类器的淘汰过程中考虑了各个分类器对集成分类的贡献.
本文的主要结构如下:第2节总结相关的研究工作并给出所涉及的基本概念.第3节阐述本文提出的算法.在第4节中对所提出的算法进行实验并进行性能分析.第5节进行全文总结以及对进一步工作的展望.
2 面向数据流的集成式分类研究背景
2.1 相关概念
数据流可表示为S={s1,s2,…,st,…},其中st=(xt,yt)为t时刻(t= 1,2,…,T)的实例,xt∈(Rd是特征向量,yt∈ {c1,c2,…,ck}是类值,k(k>1)为S中所包含的类值数.根据源源不断到达的实例,增量式的学习并产生了一个分类器f,并来对类别标记未知的实例预测类值.
目前,大多数文献大多数都采用概率来定义概念.在本文将概念定义为联合分布P(X,y).输入变量和目标变量之间联合概率的变化的现象称为概念漂移,因此t0和t1时刻之间的概念漂移可表示为:
∃X:Pt0(X,y)≠Pt1(X,y)
(1)
如图1所示,用一维数据的均值变化来展示漂移发生过程.若数据流中数据分布在较短的时间内被另一个数据分布所取代,则称此时发生了突变式概念漂移[6].而渐变式概念漂移是一种慢速率改变(如传感器部件逐渐失灵),概念漂移发生前后概念之间有或多或少的相似[6].
2.2 相关工作
近年来,随着类不平衡数据问题研究的不断深入,数据流中的类不平衡问题也吸引了大量的研究者.Gao等人中提出一个数据流中类不平衡问题的集成分类框架,改算法采用过采样技术来处理不平衡问题[14].文献[15]中提出一种处理不平衡数据流的方法,该方法不仅增加了正类实例,而且增加被错误分为负类实例,同时,该方法还提出一种新的定义正类和负类的边界的方法,以提高分类器的集成效果.欧阳震净等人结合基于权重的集成分类器与抽样技术,提出了一种处理不平衡数据流集成分类器模型[16].最近,Ditzler等人提出了基于集成学习的方法Learn++.CDS和Learn++.NIE来解决类不平衡数据流中的概念漂移问题[17].Mirza等人提出了一种基于极端学习机(Extreme Learning Machine,ELM)的集成方法,该方法是以数据块为单位来处理数据流的[18],但并未考虑概念漂移问题.
类不平衡问题常常会和概念漂移一起存在于数据流中,然而上述算法大多只是针对其中一个问题进行研究的,并未充分考虑同时存在类不平衡和概念漂移现象的问题.
2.3 基于数据块的数据流集成方法
令S表示数据流,在基于数据块的集成分类方式中,将S平均分成若干个大小相等数据块B1,B2,…,Bn,数据块大小为d.不断地在新到的数据块Bi上建一个新分类器C′,添加到集成分类器中,以替换性能最差的分类器,从而适应数据流分布变化的需要,并采用加权投票等原则预测实例.基于数据块的分类器集成方法的一般过程如算法1所示.
算法1.基于数据块的集成分类框架
输入:S:数据流,d:数据块的大小,k:基分类器个数,Q(·):分类器性能度量函数
输出:ε:包含k个分类器的集成分类器
01:begin
02:for 数据块Bi∈Sdo
03: 在Bi上训练新分类器,并利用Q(·)计算其权值
04: 在Bi上根据Q(·)给E中所有分类器赋权值
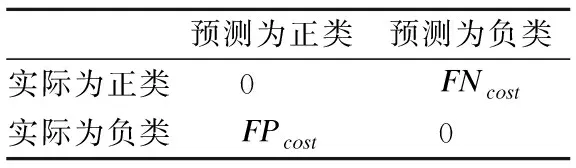
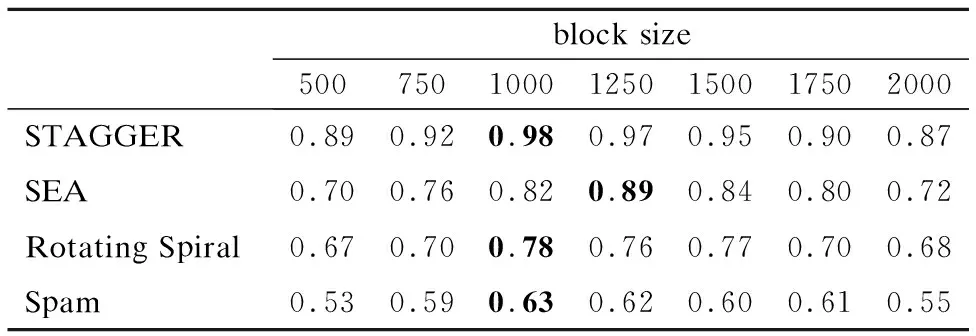
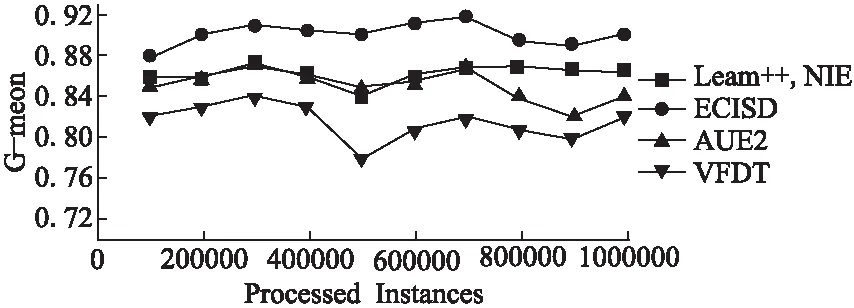
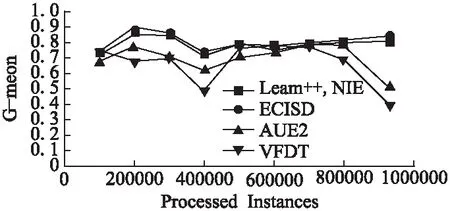
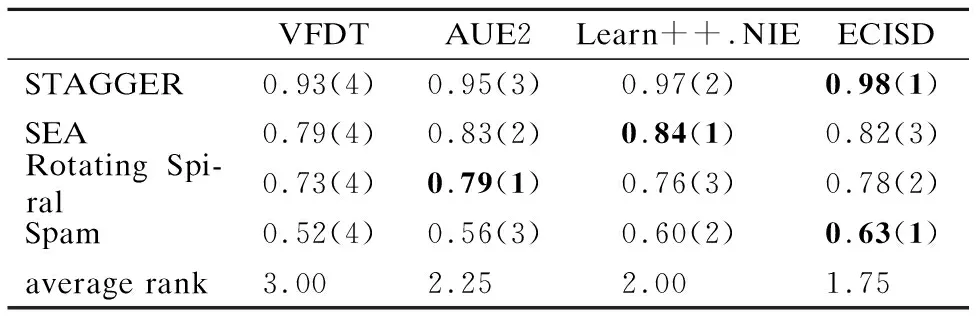
05: if |ε| 06:ε←ε∪{C′} 07: else if ∃i:Q(C′)>Q(Ci) then 08: 用C′替换ε中性能最差的分类器 09: end if 10:end for 11:end 如何动态更新分类器的权重是此类数据流集成分类方法研究的关键[19].Street等提出了数据流集算法(Streaming Ensemble Algorithm,SEA)[20],此算法不断的在最新数据块上训练新的基分类器,并采用启发式策略替换性能最差的分类器,从而适应概念漂移.Wang等人提出了一种基于准确率加权集成(Accuracy Weighted Ensemble,AWE)算法[2],以基分类器Cj在当前最新数据块Bi上的误差率作为加权的依据,其加权函数如公式(2)所示. (2) (3) 近年来,集成学习模型被广泛用于处理概念漂移问题.Wang等人[2]从理论上证明了集成分类器的性能要优于单个分类器.为此,本文提出了一种基于集成的不平衡数据流分类算法(Ensemble Classifiers for Imbalanced Streaming Data,ECISD),来处理数据流中的概念漂移和类不平衡问题. 图2 算法流程图Fig.2 Flow chart of ECISD 简单起见,本文只考虑两类的情况,可以扩展到多类的情况,其基本过程如图2所示.算法主要包括两个步骤: 1)数据采样阶段:采用SMOTE和Tomek Links相结合的方式,达到在增加正类样本的目的,同时也减少负类样本的目的,从而平衡各个类别. 2)集成分类阶段:利用集成的方式对数据流进行分类,并综合考虑了基分类器在最新的数据块上的分类错误情况和分类错误的代价来动态更新各分类器的权重.并用最新分类器替换贡献值最小的基分类器. 由于SMOTE方法生成的正类样本是通过线性差值得到的,在平衡类别分布的同时也会扩张了少数类的样本空间,这样一来,原本属于负类样本的空间可能会被正类样本侵占,同时容易造成模型的过拟合.而Tomek Links方法删除的是边界点或噪声点,因此可以用于解决SMOTE方法中存在的问题.伪代码如算法2所示. 算法2.样本采样算法 输入:T:正类样本数,N%:过采用百分比,q:最近邻数量 输出:采样后新样本集合 01:begin 02:numattrs=属性数 03:Sample[ ][ ]:原始正类样本数组 04:newindex:新合成的人工样本数量 05:Synthetic[ ][ ]:合成样本数组 06:fori←1到T 07: 计算第i个正类样本的q个最近邻并保存到数组nnarray中 08: 生成人工合成的样本(N,i,nnarray) 09:end for 10:找到样本集合中的Tomek link对 11:删除Tomek link对中的负类样本 12:end 令S表示数据流,将S平均分成若干个大小相等数据块B1,B2,…,Bn,数据块大小为d.不断地在新到来的数据块Bi上新建一个分类器C′.给新建的分类器赋予一个权值wC′.对于集成分类器ε={C1,C2,…Cm}中每一个分类器Cj,首先通评价它在最新数据块上的分类性能来动态更新分类器权值,同时考虑到它分类错误的代价,接着将新建的分类器加入ε中.若此ε中分类器数达到最大允许数k时,则淘汰使集成分类正确率的降低的分类器.采用加权投票的方式对数据流中的实例的进行预测. 3.3.1 基分类器加权策略 在加权过程中考虑到分类错误的代价,即引入一个代价矩阵,如表1所示. 表1 代价矩阵Table 1 Cost matrix 其中,FPcost为将负类分为正类产生的代价,FNcost表示将正类分为负类产生的代价.一般来说FPcost 设将实际类别为y的实例x分为y′类的代价为Jy,y′(x),Cj在数据块Bi上误分类总代价如公式(4)所示: (4) 分类器Cj在数据块Bi上的权值wij如公式(5)所示: (5) 其中,α是一个很小的正数,为了避免出现分母为0的情况.最后,所有基分类器的权重还需要进行归一化处理. 3.3.2 基分类器淘汰策略 每当到达一个新数据块后,就根据已有的基分类器在最新数据块上分类情况进行评价.集成分类器的整体正确率如公式(6)所示: (6) 其中xl是Bi中的实例,Gε(xl)的定义如公式(7)所示: (7) 若将分类器Cj从ε中移除,此时集成分类器的分类正确率就如公式(8)所示: (8) Cj在Bi上对集成分类器的分类正确率的贡献Conε(j)如公式(9)所示: Conε(j)=Pε(Bi)-Pε-Cj(Bi) (9) 该值可以为正也可以为负.Conε(j)为负值,表示该分类器降低了整体的分类正确率,Conε(j)如果为正值,表示该基分类器可以提高整体的分类正确率.每当加入一个新建的分类器,就删除Con值为负的分类器. 3.3.3 ECISD算法的描述 ECISD算法描述如算法3所示. 算法3. ECISD 输入:S:数据流,k:集成分类器中的分类器数 输出:ε:包含k个带权值分类器的集成 01:begin 02:ε←φ 03:forBi∈Sdo 04: 在Bi上训练新的分类器 06: forCj∈εdo 07: 计算MSEij,ctij,MSEr 09: 计算Conε(j) 10: ifConε(j)<0 then 11: 删除Cj 12: end if 13: end for 14: if |ε| 15:ε←ε∪{C′} 16: else 17: 用C′替换ε中Con值最低的分类器 18: end if 19: forCj∈ε/{C′} do 20: 增量地在Bi上训练分类器Cj 21: end for 22:end for 23:end. 本文算法均在大规模数据在线分析开源平台MOA(Massive Online Analysis)[23]下实现.实验程序是在CPU为2.8GHZ,内存为8GB,操作系统为Windows 7的PC机上进行实验的. 实验选取3个人工合成数据集和1个真实数据集: 1)STAGGER数据集,由Schlimmer等人提出,常被用来衡量分类器在概念漂移数据流上的分类性能.实验中采用MOA中的数据流产生器STAGGERGenerator生成包含1000,000个实例的数据集.该数据集中有3个概念,漂移类型是突变式的,对于第一个概念,两个类的不平衡比例为7,另外两个概念是平衡的. 2)SEA是经典的突变式概念漂移数据集.其基本结构是 3)Rotating Spiral数据集:这是一个合成数据集,其中描述了4种螺旋.该数据集中的漂移类型是渐变式的.该数据集包含1000,000个实例,其中正类实例大约占5%. 4)Spam数据集包含9,324个实例,每个实例有500个属性用于表示一个邮件的信息,被分为两种类型:垃圾邮件(仅占20%)和合法邮件,因此该数据集既是一个不平衡数据集,同时数据集中的垃圾邮件的特征随着时间缓慢变化即包含概念漂移*该数据集可在http://mlkd.csd.auth.gr/concept_drift.html下载.用MOA中的ArffFileStream产生器将静态的数据模拟产生数据流. 所提算法与以下3个算法进行对比:VFDT(Very Fast Decision Tree)[24]、AUE2和Learn++.NIE.VFDT是一种从数据流中增量式的生成决策树的单分类器算法,利用Hoeffding不等式理论,能够以一定的概率保证所构造决策树的精度.为了便于比较,集成分类中分类器数k=15,基分类器为Hoeffding Tree,选取与文献[24]相同的参数.本文所提出的算法的参数设置为:d= 1000,N= 300,q= 6;AUE2采用MOA中的默认设置.采用G-mean作为算法的评价指标,如公式(10)所示. (10) G-mean是分类器对正类样本的分类精度(召回率)与对负类样本分类准确度的几何平均值.此指标常用于衡量不平衡数据流分类效果. 4.2.1 数据块大小对算法性能影响 在STAGGER数据集上进行测试,为了验证数据块大小设置对算法性能的影响分别取值为[500,2000].由图3可以看出,在一开始,随着数据块的增大使得构建分类器的数据增多,平均G-mean值也随之上升.然而,随着数据块的继续增大,概念漂移发现滞后,平均G-mean值反而略有降低.表2表明本文所提的方法受窗口大小设置影响很小,当数据块大小为1000时可以获得相对较高的G-mean值. 图3 不同数据块大小的平均G-mean值比较Fig.3 Average G-mean using different block sizes 表2 不同大小数据块下的平均G-mean值Table 2 Average G-mean using different block sizes 4.2.2 不同算法性能比较分析 首先,在人工合成数据集上验证所提算法的有效性.图4是算法在STAGGER数据集上分类得到的G-mean值.我们观察发现,所有算法变化趋势基本一致.其中,Learn++.NIE算法和ECISD算法在该数据集上的性能较好,VFDT的性能最差.VFDT算法在第400,000个实例附近的G-mean值波动很大,同样的情况也发生在第800,000个实例附近.这是由于基于数据块的算法不断在最新数据块上训练生成分类器,同时算法采用了周期加权机制,增加对最新数据的适应性,更适合具有概念漂移的环境.同时本文算法是基于基分类器性能和误分类代价的,在分类之前加入采样方法应对类不平衡问题,从而提高分类器的性能.而VFDT没有任何处理概念漂移机制,因此不适合概念漂移环境. 图4 在STAGGER数据集上的G-mean值Fig.4 G-mean on STAGGER dataset 图5展示了算法在SEA数据集上的性能.从图中可以看出,VFDT算法的性能最差,ECISD在该数据集上的性能较差,尤其在第500,000个实例附近,所有算法的G-mean值都急剧下降除了本文算法.本文算法能快速捕捉到概念变化,并建立新的分类器,从而及时应对这种变化. 图5 在SEA数据集上的G-mean值Fig.5 G-mean on SEA dataset 图6展示了算法在集Rotating Spiral上的性能.可以看出所有算法变化趋势基本一致,波动都较大.VFDT算法性能最差,其他3种算法的性能都比VFDT要好,这是由于本文算法采用对实时数据流环境的数据不平衡问题的调节策略与方法,在数据的处理过程中采用数据采样方法策略以调节正例和反例在整个模型或算法中的贡献,保证算法或模型能及时有效地适应数据流的变化接着,在真实数据流数据集上验证所提算法的有效性.图7反应了在真实数据集Spam上的性能,所有算法的G-mean曲线均出现不同程度的波动,而本文算法和Learn++.NIE算法的曲线相对平稳,受到数据中概念漂移影响最小,表明算法对真实的数据环境有较好的适应性.而VFDT算法和AUE2算法的性能较差. 图6 在Rotating Spiral数据集上的G-mean值Fig.6 G-mean on Rotating Spiral dataset 图7 在Spam数据集上的G-mean值Fig.7 G-mean on Spam dataset 最后,我们来分析算法在4个数据集上的平均G-mean值.从表3可以看出ECISD在STAGGER和Spam数据集上的平均性能最好,在SEA上的性能较差,并且ECISD算法的平均排名最高.这是由于ECISD算法既可以处理类不平衡问题又可以处理概念漂移问题.VFDT算法不能处理类不平衡问题,同时它也没有处理概念漂移的机制,因此它的平均性能最差. 表3 算法的平均G-mean值Table 3 Average G-mean of algorithms 针对数据流分类中的概念漂移和类别不平衡问题,提出了一种基于集成学习的不平衡数据流分类算法.在降低数据流不平衡分布的基础上,考虑不同类型概念漂移的特征,设计基于不同类型的概念漂移的解决方案.通过实验验证了所提算法能够在不平衡的概念漂移数据流上取得较好的分类效果. 由于本文提出的算法是以数据块为单位进行处理的,存在数据块大小选择的问题.因此如何设计自适应数据块大小的集成算法,是今后值得进一步研究的方向. : [1] Gama J.Knowledge discovery from data streams[M].New York:CRC Press,2010. [2] Wang H,Fan W,Yu P S,et al.Mining concept-drifting data streams using ensembles classifiers[C].Proceedings of Ninth ACM SIGKDD International Conference on Knowledge Discovery and Data Mining(KDD 2003),2003:226-235. [3] Cohen L,Avrahami-Bakish G,Last M,et al.Real-time data mining of non-stationary data streams from sensor networks[J].Information Fusion,2008,9(3):344-353. [4] Widmer G,Kubat M.Learning in the presence of concept drift and hidden contexts[J].Machine Learning,1996,23(1):69-101. [5] Webb G I,Hyde R,Cao H,et al.Characterizing concept drift[J].Data Mining and Knowledge Discovery,2016,30(4):964-994. [6] Tsymbal A.The problem of concept drift:Definitions and related work[R].Technical Report TCD-CS-2004-15,Trinity College Dublin,2004. [8] Qi Kai-yuan,Zhao Zhuo-feng,Fang Jun,et al.Real-time processing for high speed data stream over large scale data[J].Chinese Journal of Computers,2012,35(3):477-490. [9] He H,Garcia E A.Learning from imbalanced data[J].IEEE Transactions on Knowledge and Data Engineering,2009,21(9):1263-1284. [10] Chawla N V,Bowyer K W,Hall L O,et al.SMOTE:synthetic minority over-sampling technique[J].Journal of Artificial Intelligence Research,2002,16:321-357. [11] Ling C X,Sheng V S,Yang Q.Test strategies for cost-sensitive decision trees[J].IEEE Transactions on Knowledge and Data Engineering,2006,18(8):1055-1067. [12] Sun Y,Kamel M S,Wong A K C,et al.Cost-sensitive boosting for classification of imbalanced data[J].Pattern Recognition,2007,40(12):3358-3378. [13] Wang S,Yao X.Diversity analysis on imbalanced data sets by using ensemble models[C].Proceedings of the IEEE Symposium Series on Computational Intelligence and Data Mining(CIDM 2009),2009:324-331. [14] Gao J,Fan W,Han J,et al.A general framework for mining concept-drifting data streams with skewed distributions[C].Proceedings of the 2007 SIAM International Conference on Data Mining,2007:3-14. [15] Chen S,He H.Towards incremental learning of nonstationary imbalanced data stream:a multiple selectively recursive approach[J].Evolving Systems,2011,2(1):35-50. [16] Ouyang Zhen-jing,Luo Jian-shu,Hu Dong-min,et al.An ensemble classifier framework for mining imbalanced data streams[J].Chinese Journal of Electronics,2010,38(1):184-189. [17] Ditzler G,Polikar R.Incremental learning of concept drift from streaming imbalanced data[J].IEEE Transactions on Knowledge and Data Engineering,2013,25(10):2283-2301. [18] Mirza B,Lin Z,Toh K A.Weighted online sequential extreme learning machine for class imbalance learning[J].Neural Processing Letters,2013,38(3):465-486. [19] Gomes H M,Barddal J P,Enembreck F,et al.A survey on ensemble learning for data stream classification[J].ACM Computing Surveys(CSUR),2017,50(2):1-36. [20] Street W N,Kim Y S.A streaming ensemble algorithm(SEA) for large-scale classification[C].Proceedings of the Seventh ACM SIGKDD International Conference on Knowledge Discovery and Data Mining,ACM,2001:377-382. [21] Brzeziński D,Stefanowski J.Accuracy updated ensemble for data streams with concept drift[C].Proceedings of the 6th International Conference on Hybrid Artificial Intelligent Systems(HAIS 2011,LNCS 6678),Berlin:Springer-Verlag,2011:155-163. [22] Brzezinski D,Stefanowski J.Reacting to different types of concept drift:the accuracy updated ensemble algorithm[J].IEEE Transactions on Neural Networks and Learning Systems,2014,25(1):81-94. [23] Bifet A,Holmes G,Kirkby R,et al.MOA:massive online analysis[J].Journal of Machine Learning Research,2010,11(5):1601-1604. [24] Domingos P,Hulten G.Mining high-speed data streams[C].Proceedings of the Sixth ACM SIGKDD International Conference on Knowledge Discovery and Data Mining,2000:71-80. 附中文参考文献: [8] 亓开元,赵卓峰,房 俊,等.针对高速数据流的大规模数据实时处理方法[J].计算机学报,2012,35(3):477-490. [16] 欧阳震净,罗建书,胡东敏,等.一种不平衡数据流集成分类模型[J].电子学报,2010,38(1):184-189.
3 一种基于集成学习的不平衡数据流分类算法
3.1 基本思想

3.2 样本采样过程描述
3.3 基于集成学习的不平衡数据流分类算法

4 实验评价
4.1 数据集描述
4.2 参数设置与实验结果分析



5 总结与展望


