置信规则库参数训练的布谷鸟搜索算法

李 敏,傅仰耿,刘莞玲,吴英杰

(福州大学 数学与计算机科学学院,福州 350116)

1 引 言

基于证据推理算法的置信规则库推理方法(belief rule-base inference methodology using the evidence reasoning approach,RIMER)是在Dempster-Shafer理论[1,2]、决策理论[3]、模糊理论[4]和传统IF-THEN规则[5]的基础上发展起来的,能有效处理带有含糊(vagueness)或不确定性、不完整的数据[6].目前,该方法已经成功应用在工程系统的安全评估[7]、输油管道的检漏[8]和石墨成分的检测[9]等领域.

针对BRB系统的参数优化问题,传统的方法主要有:近似线性法、Zoutendijk可行方向法以及Wolfe简约梯度法等[10],但这些传统的方法存在实现复杂、收敛精度低等缺陷.后来,Yang等[9]首次提出了BRB的参数优化模型.而后专家们在此方向上相继提出了基于梯度下降算法[11]、基于变速粒子群算法[12]、基于差分进化算法[13]和基于改进粒子群算法[14]等的参数训练模型.这些参数训练模型已经能有效解决一些由于参数设置不合理导致的推理准确性低的问题,但是现有的这些方法仍然存在一些不足,如系统实现过于复杂、收敛效率不佳以及易陷入局部最优等.因此,为了使BRB系统具有更好的推理效率和推理准确性,研究更加通用和有效的置信规则库参数学习方法是很有必要的.

鉴于此,本文结合布谷鸟搜索 (CS) 算法[15],提出了基于自适应扰动布谷鸟搜索算法的置信规则库参数优化方法.该算法的本质是利用布谷鸟搜索算法求解优化模型,但标准的布谷鸟搜索算法鲁棒性不佳,易早熟,易陷入局部最优解.为此本文引入自适应扰动策略,增加算法中每一代个体之间的差异性,并控制迭代过程中个体的活动范围,从而优化种群的进化过程并得到更优的精度.在实验分析中,本文首先通过拟合多极值函数的实验,与其他现有方法进行比较,从而验证自适应扰动布谷鸟搜索算法能够取得更好的收敛精度与收敛速度;最后将该算法应用于输油管道检漏的实例中,并与其他现有的方法进行比较,进一步验证本文改进的方法对实际问题具有良好的适用性.

2 置信规则库推理方法与问题提出

2.1 BRB的表示

BRB中的置信规则在IF-THEN规则的基础上增加了分布式置信框架,并为前件属性和规则都设置相应的权重,下式给出第k条规则的表示:

(1)

Witharuleweightθkandattributeweightδ1,k,δ2,k,…,δTk,k

2.2 RIMER方法的推理机制

2.2.1 激活权重的计算

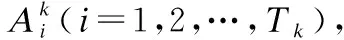
(2)

对于第k条规则激活权重的求解方法为:

(3)

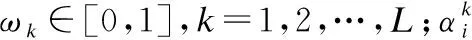
2.2.2 修正置信度

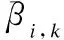
(4)

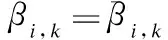
2.2.3 合成激活规则

根据ER算法,属性的可信度可以通过每条规则的置信度与属性权重算出,具体公式如下:

mn,i=ωiβn,i

(5)

(6)

(7)

(8)

上式中n=1,…,N,i=1,…,L.

在求得基本可信度之后,运用ER算法的解析式[17]就能合成全部的基本属性,具体公式为:

(9)

(10)

(11)

(12)

接着,可算出新合成属性的结果评价等级置信度,其具体公式为:

(13)

(14)

式中βn和βH分别表示评价类型Dn对应的置信度和不完备信息的置信度.

最后,如果要求输出的结果是简单的数值类型时,可以计算出置信规则库系统的期望效用值.假设等级效用值为μ={μ1,μ2,…,μN},则BRB系统的效用值计算公式如下:

(15)

2.3 BRB的参数训练模型

Yang等提出的BRB参数学习的模型[9]如图1所示.

图1 BRB参数训练模型Fig.1 Model of BRB parameter training

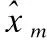
min{ξ(P)}
s.t.A(P)=0,B(P)≥0

(16)

Yang的BRB参数训练模型中,每个参数的约束条件如下:

1)BRB中结果评价等级的置信度取值范围为[0,1],第k条规则中的第n个结果评价等级对应置信度应符合下式的限制范围:

0≤βn,k≤1,n=1,2,…,N;k=1,2,…,L

(17)

2)假设第k条规则的输入信息具有完整性,那么置信度的总和为1.

(18)

3)第k条规则的贡献值θk进行归一化后,θk的值应该在0到1之间.

0≤θk≤1,k=1,2,…,L

(19)

(20)

同理,BRB系统的仿真输出可表示为:

(21)

则BRB参数优化模型对应的目标函数是:

(22)

置信规则库的推理输出和真实输出之间的偏差通常可以用均方差进行衡量,由此可得目标函数为:

(23)

2.4 问题提出

通过对置信规则库推理过程的研究可以发现,BRB系统的参数直接影响着最终的推理精度.但现有的BRB系统的参数学习方法仍然存在一些不足.例如:Yang等[9]基于使用Matlab中FMINCON函数的参数学习方法,由于受限于FMINCON函数,不仅求解的效率慢,而且准确度较低;常瑞等[16]采用的将梯度下降法与二分法相结合的参数优化方法只对BRB中的部分参数做局部优化.吴伟昆等[11]在此基础上进行进一步研究,提出了基于加速梯度求法的置信规则库参数学习方法,虽然对算法的运行效率与精度都取得了一定的改进,但改进过程中也增加了算法实现的复杂度.而后王韩杰等[13]在差分进化算法的基础上加入专家干预,提出了专家干预下的置信规则库参数学习方法.苏群等[12]在粒子群算法的基础上通过加入粒子的变速操作,提出了基于变速粒子群算法的置信规则库参数学习方法.但是这两种涉及群智能算法的改进,在收敛效率和收敛精度方面还不够理想,当实际问题对于效率与精度有更高的要求时,这些算法无法满足需要.因此,本文提出基于布谷鸟搜索算法[15]的参数训练方法来对BRB的内部参数进行训练,最后在此基础上构建BRB系统,从而提升BRB系统的推理效率与推理准确性.

3 基于自适应扰动布谷鸟搜索算法的参数训练

3.1 自适应扰动的布谷鸟算法

布谷鸟搜索(CS)算法是剑桥大学Yang和S.Deb受到布谷鸟育雏和寻巢的习性启发而提出的一种群智能算法[15].布谷鸟在育雏时具有寄生育雏(Brood Parasitism)的习性,而在移动中则具有莱维飞行(Levy flight)的特征,该算法通过对这两种行为的模拟来有效地求解最优化问题[18].

标准的布谷鸟搜索算法采用飞行与遗弃并寻找新巢这两种方式对个体进行更新:

1)通过Levy flight对当前个体进行更新,具体公式为:

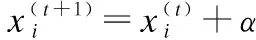
(24)

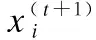
L(λ)～u=t-λ,1<λ≤3

(25)

在Levy flight随机取值后,可将当前个体中最优的个体作为参考值进行移动,最终的移动公式如下所示:

(26)

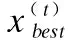
(27)

式中:Г为标准Gamma函数.

2)对于适应值较差的鸟巢,由迁移概率Pa判断该鸟巢是否需要被遗弃并寻找新位置.新位置的生成方式如下:

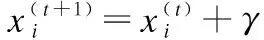
(28)

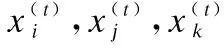
3)为增加种群的多样性,本文引入一种新的更新种群方法,即自适应扰动.

(29)

3.2 新参数训练方法的算法步骤

本文提出的基于布谷鸟搜索算法的参数训练算法流程如下:

具体步骤如下:

步骤1.初始化鸟巢.确定种群规模与迁移概率,并在已知的限定条件内随机选取鸟巢的初始位置.

步骤2.计算鸟巢的适应值.根据实际问题设置目标函数,并以此求出各个鸟巢位置的适应值.

步骤3.依次从当前各个鸟巢出发进行Levy flight,由式(26)计算出飞行后的新位置.之后对鸟巢各个维度上超出限定条件的数值进行修正,防止出现鸟巢位置超出搜索空间的情况.

步骤4.根据迁移概率Pa对鸟巢进行迁移,根据式(28)计算出鸟巢的新位置.

步骤5.根据式(29)对当前鸟巢进行自适应扰动,寻找更优的位置.

步骤6.如果当前更新次数未达到初始给定的次数,则返回步骤3;否则将当前最优解保留并设置为BRB系统的参数,算法结束.

图2 布谷鸟搜索算法参数训练流程图Fig.2 Flow chart of the CS algorithm parameter training

4 实验分析

实验部分,本节通过两个实例验证本文提出的参数学习方法有效性,并与现有的参数学习方法进行比较.实验环境为:Intel(R) Core(TM) i5-4570 @ 3.20GHz CPU、8GB内存,Windows 7操作系统.

4.1 多极值函数实例

首先以多极值函数来验证基于布谷鸟搜索算法的参数学习方法的可行性,多极值函数的具体式子如下:

g(x)=e-(x-2)2+0.5e-(x+2)2

(30)

式中,g(x)大约在x=0存在一个局部最小值,在x=-2,x=2处分别有一个局部最大值和一个全局最大值.基于观察到的这些关键点的输出,置信规则的结果定义为:

{D1,D2,D3,D4,D5}={-0.5,0,0.5,1,1.5}

(31)

进行参数训练时,选取该函数上1000个均匀分布的点作为训练集,设定种群的大小为25,将均方误差MSE作为目标函数.

对比图3、图4中曲线的拟合效果可以发现,初始BRB系统拟合函数的效果非常不理想,因此引入参数学习是必要的.而图4表明采用布谷鸟搜索算法能够更好地解决陷入局部最优的问题,训练后的BRB系统推理准确性更高,拟合多极值函数的效果更好.

未经参数学习的BRB系统拟合函数效果如图3所示.

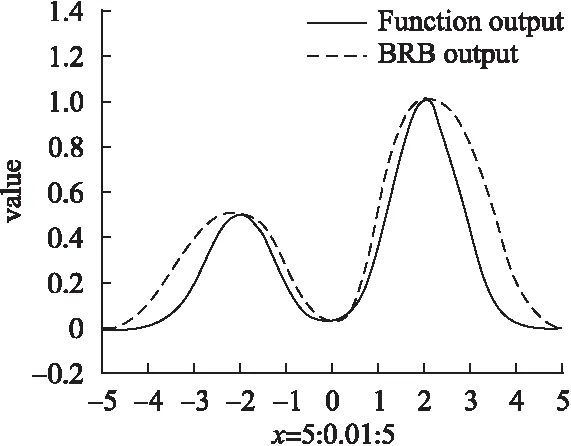
图3 初始BRB系统的拟合效果Fig.3 Results of initial BRB system

采用基于布谷鸟搜索算法训练后的BRB系统拟合多极值函数的效果为图4所示.

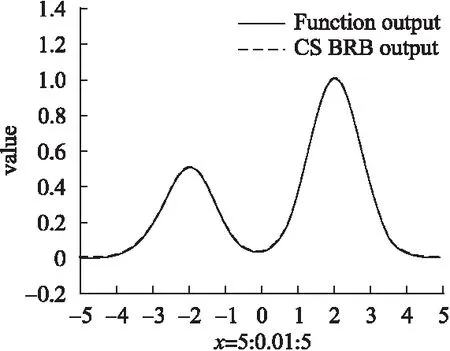
图4 基于布谷鸟搜索算法的BRB函数拟合结果Fig.4 Results of BRB based on the CS algorithm

对比传统FMINCON方法的BRB系统进行拟合的多极值函数与本文提出算法的均方误差(MES)差异如图5所示.

图5 Fmincon与CS BRB以及标准CS BRB拟合结果的MES对比Fig.5 Compare of BRB parameters based on Fmincon,CS BRB and standard CS BRB

由图5可知,基于自适应扰动布谷鸟搜索算法的BRB系统相比基于Fmincon函数的BRB系统以及标准的布谷鸟搜索算法的BRB系统取得了更好的推理准确性.

根据文献[16]可以得到初始BRB规则库如表1所示,由布谷鸟搜索算法训练后的BRB规则库如表2所示.

在表3中进一步对比了本文方法与传统的FMINCON方法[20]、Chen的方法[19]及Wang的方法[13]的收敛精度和收敛时间.由表3可知本文提出的新方法相比于Fmincon函数、Wang的专家干预下基于差分进化算法的参数学习方法和Chen的局部优化参数训练方法[19]具有更好的推理精度.而且Fmincon函数依赖于Matlab不易移植且耗时,可见本文方法更为有效.

表1 初始置信规则库Table 1 Initial BRB

4.2 输油管道检漏实例

为了检验基于布谷鸟搜索算法的BRB参数学习方法解决实际问题时的能力,本文采用输油管道检漏实例[6]进行实验分析.实验选用英国的一条100多公里长的输油管道的石油泄漏数据来进行实验.

对于输油管道系统,在正常工作时,若油液输入量大于输出量,那么油液对管道产生的压力与管道中油液总量成正比例关系;在不满足正常工作模式时,输入量大于输出量,压力反而减小,那么该系统可能已发生泄漏故障.由此可见,输油管道内的平均压力(PD)和流量的差值(FD)能够直观地反应输油管道的泄漏状况.

表2 训练后的置信规则库Table 2 BRB after training

表3 BRB系统推理性能的比较Table 3 Performance comparison of BRB System in function fitting

对于初始BRB的构建,以输出流量差(Flow Difference,FD)和管道内平均压力(Pressure Difference,PD)作为前件属性,FD有8个参考值、PD有7个参考值.并选取泄漏量的大小(Leak Size,LS)作为系统输出,共分为5个评价等级.前件属性FD、PD和结果集LS经过量化后,候选值可表示为如下形式:

FD={-10,-5,-3,-1,0,1,2,3}

(32)

PD={-0.042,-0.025,-0.01,0,0.01,0.025,0.042}

(33)

LS={0,2,4,6,8}

(34)

由FD和PD可得到56条置信库规则参数,从而组成BRB系统[19],实验时,以2007组数据作为测试集,并随机选取其中500组数据作为训练集,以平均绝对误差MAE作为目标函数.未训练BRB系统对输油管道进行检漏的效果为图6.

由图6可知未训练的BRB系统因参数设置不合理,拟合输油管道泄漏时误差大,所以要对初始BRB的参数进行训练优化.

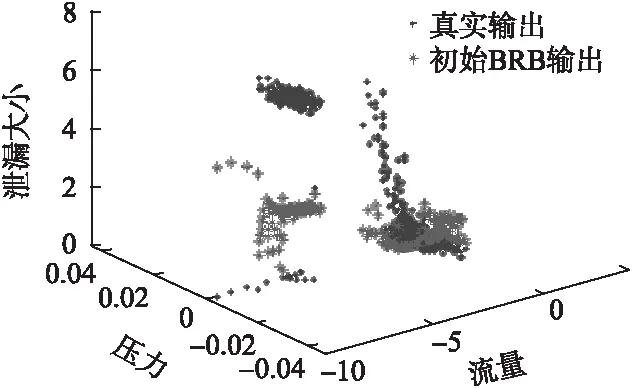
图6 未训练的BRB系统输出与训练数据Fig.6 Results of initial BRB system

训练后的BRB系统的推理结果如图7所示.

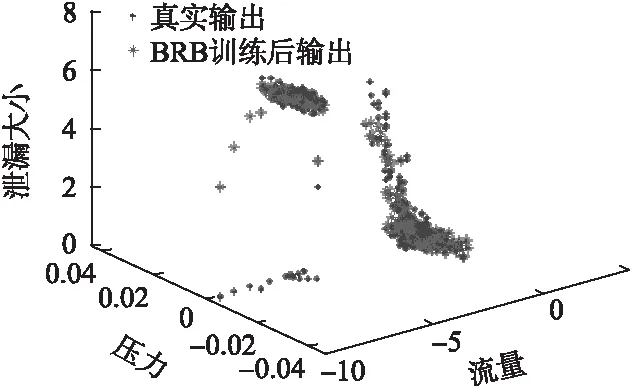
图7 训练后的BRB系统输出与训练数据Fig.7 BRB system outputs after training

从图7中可以得到本文提出的方法训练后的BRB系统能准确地拟合输油管道泄漏的真实情况,训练后系统的推理准确性到了极大的提升.

未训练的BRB系统拟合的输油管道泄漏情况为图8所示.

使用FMINCON函数的参数训练方法来拟合输油管道泄漏的效果为图9所示.

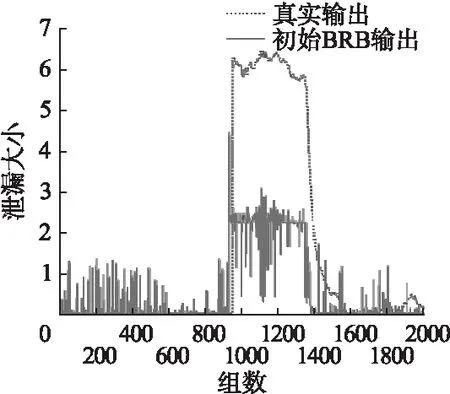
图8 未训练BRB系统对输油管道系统泄漏的拟合情况Fig.8 Results of initial BRB system

由图8、图9和图10可知,与初始BRB和利用FMINCON函数训练后的BRB系统相比,本文所提出的新方法训练后的BRB系统具有更好的决策推理能力,能够很好反映输油管道泄漏的实际情况,并且没有出现过拟合的现象.

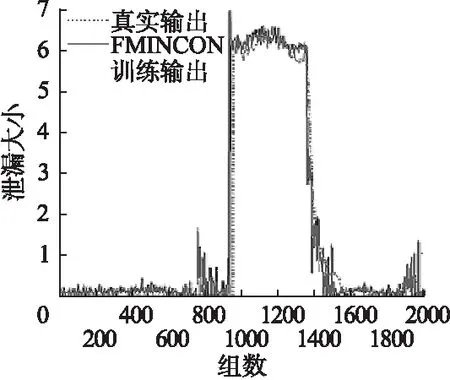
图9 利用FMINCON函数参数训练后BRB系统的拟合结果Fig.9 Results of BRB parameters based on FMINCON function

使用基于布谷鸟搜索算法的参数学习方法进行输油管道泄漏的拟合结果为图10所示.

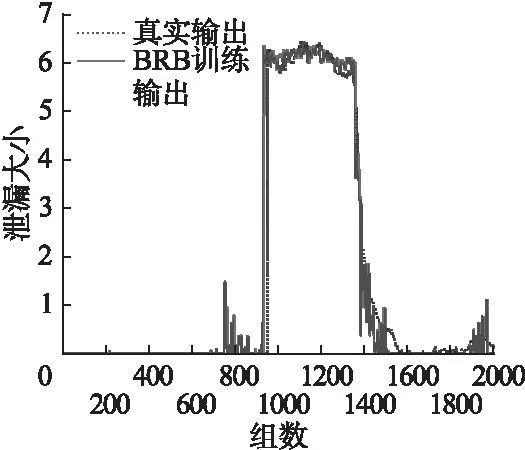
图10 基于布谷鸟搜索算法训练后的BRB系统的拟合结果Fig.10 Results of BRB parameters based on the CS algorithm

为了进一步说明新方法的性能,实验中将现有的参数学习方法作为比较对象,实验仍为输油管道泄漏检测实例,对比结果如表4所示.

根据表4中MAE以及算法运行时间的对比,可以得出采用本文所提新方法进行训练后的BRB系统推理精度高于其他现有的方法,同时收敛速度也相对更快,因此,本文提出的新方法综合效益更高.

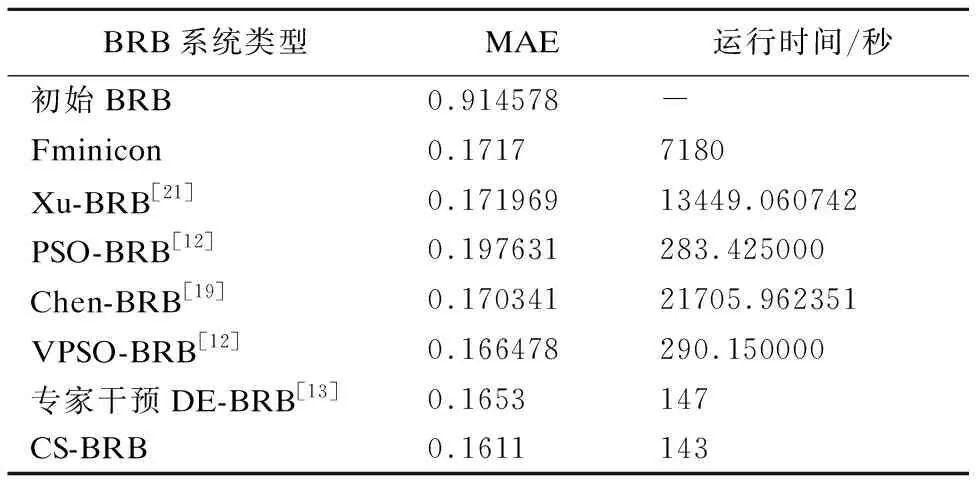
表4 BRB系统推理性能的比较Table 4 Comparison of reasoning performance of BRB system

5 结 语

针对现有BRB参数学习优化模型存在的不足,本文提出基于布谷鸟搜索算法的BRB参数学习方法,并通过多极值函数与输油管道泄漏两个实验验证了新方法的有效性.在多极值函数的实验中,与现有其他方法在推理精度和运行时间进了对比,实验表明,本文方法具有更好的收敛速度与精度.同时,通过输油管道泄漏的实验进一步表明了本文方法在解决真实问题时是高效可行的.

：

[1] Dempster A P.A generalization of Bayesian inference[J].Journal of the Royal Statistical Society-Series B,1968,30(2):205-247.

[2] Shafer G.A mathematical theory of evidence[M].Princeton:Princeton University Press,1976.

[3] Huang C L,Yong K.Multiple attribute decision making methods and applications,a state-of art survey[M].Berlin:Springer-Verlag,1981.

[4] Zadeh L Z.Fuzzy sets[J].Information and Control,1965,8(3):338-353.

[5] Sun R.Robust reasoning:integrating rule-based and similarity-based reasoning[J].Artificial Intelligence,1995,75(2):241-295.

[6] Zhou Zhi-jie,Yang Jian-bo,Hu Chang-hua,et al.Belief rule based expert system and complex system modeling:1stedition[M].Beijing:Science Press,2011.

[7] Liu J,Yang J B,Ruan D,et al.Self-tuning of fuzzy belief rule bases for engineering system safety analysis[J].Annals of Operations Research,2008,163(1):143-168.

[8] Zhou Z J,Hu C H,Yang J B,et al.Online updating belief rule based system for pipeline leak detection under expert intervention [J].Expert Systems with Applications,2009,36(4):7700-7709.

[9] Yang J B,Liu J,Xu D L,et al.Optimization models for training belief-rule-based systems[J].IEEE Transactions on Systems,Man,and Cybernetics-part A:Systems and Humans,2007,37(4):569-585.

[10] Ma Chang-feng.Optimization method and Matlab programming[M].Bejing:Science Press,2010.

[11] Wu Wei-kun,Yang Long-hao,Fu Yang-geng,et al.Parameter training approach for belief rule base using the accelerating of gradient algorithm[J].Journal of Frontiers of Computer Science and Technology,2014,8(8):989-1001.

[12] Su Qun,Yang Long-hao,Fu Yang-geng,et al.Parameter training approach based on variable particle swarm optimization for belief rule base[J].Journal of Computer Applications,2014,34(8):2161-2165.

[13] Wang Han-jie,Yang Long-hao,Fu Yang-geng,et al.Differential evolutionary algorithm for parameter training of belief rule base under expert intervention[J].Computer Science,2015,42(5):88-93.

[14] Yang Hui,Wu Pei-ze,Ni Ji-liang.Belief rule base parameter training approach based on improved particle swarm optimization[J].Computer Engineering and Design,2017,38(2):400-404.

[15] Yang X S,Deb S.Cuckoo search via Levy flights[C].Proceedings of World Congress on Nature & Biologically Inspired Computing,India,USA:IEEE Publications,2009:210-214.

[16] Chang Rui,Wang Hong-wei,Yang Jian-bo.An algorithm for training parameters in belief rule-bases based on the gradient and dichotomy methods [J].Journal of Systems Engineering,2007,25(Sup.):287-291.

[17] Chang L,Zhou Z J,You Y,et al.Belief rule based expert system for classification problems with new rule activation and weight calculation procedures[J].Information Sciences,2016,336(C):75-91.

[18] Yang X S,DEB S.Engineering optimization by cuckoo search [J].Int′l Journal of Mathematical Modeling and Numerical Optimization,2010,1(4):330-343.

[19] Chen Y W,Yang J B,Xu D L,et al.On the inference and approximation properties of belief rule based systems [J].Information Sciences,2013,234(11):121-135.

[20] Price K.Differential Evolution vs.the functions of the 2nd ICEO[C].Proceedings of the 1997 IEEE International Conference of Evolutionary Computation,1997:153-157.

[21] Xu D L,Liu J,Yang J B,et al.Inference and learning methodology of belief-rule-based expert system for pipeline leak detection [J].Expert Systems with Applications,2007,32(1):103-113.

附中文参考文献：

[6] 周志杰,杨剑波,胡昌华,等.置信规则库专家系统与复杂系统建模:第1版[M].北京:科学出版社,2011.

[10] 马昌凤.最优化方法及其Matlab 程序设计[M].北京:科学出版社,2010.

[11] 吴伟昆,杨隆浩,傅仰耿,等.基于加速梯度求法的置信规则库参数训练方法[J].计算机科学与探索,2014,8(8):989-1001.

[12] 苏 群,杨隆浩,傅仰耿,等.基于变速粒子群优化的置信规则库参数训练方法[J].计算机应用,2014,34(8):2161-2165.

[13] 王韩杰,杨隆浩,傅仰耿,等.专家干预下置信规则库参数训练的差分进化算法[J].计算机科学,2015,42(5):88-93.

[14] 杨 慧,吴沛泽,倪继良.基于改进粒子群置信规则库参数训练算法[J].计算机工程与设计,2017,38(2):400-404.

[16] 常 瑞,王红卫,杨剑波.基于梯度法和二分法的置信规则库参数训练方法[J].系统工程,2007,25(增刊):287-291.