基于卷积神经网络的多天线Polar码联合解调-解码方案
杨梦頔,侯永宏
(天津大学 电气自动化与信息工程学院, 天津 300072)
0 引 言
香农定理[1]证明了在有噪信道上存在一种信道编码方式能够实现不超过信道容量的任意速率信息的可靠传输, 但未给出具体的实现方式。经过了数代通信人近60年的不懈努力,在2008年,Arikan[2]提出了信道极化理论,并在此基础上创新性地提出了Polar码[3],它是迄今为止唯一在理论上可以被证明达到香农界的信道编码方式。此外,Polar码的生成矩阵具有固定的结构,不会造成恶性误码传播。近年来,Polar码译码方法的研究一直是一个倍受关注的热点课题。文献[4]提出了一种系统Polar码的编译码方案,通过二次编码得到系统Polar码,与非系统码相比降低了误比特率。Tal和Vardy[5]提出了一种连续删余列表(successive cancellation list,SCL)译码算法,在每个译码阶段同时考虑多条路径,以提高Polar码译码准确度。陈凯等[6]提出了一种循环冗余校验(cyclic redundancy check,CRC)辅助的SCL译码算法,在备选路径中选出通过CRC校验的路径作为结果输出,使译码更加准确。樊婷婷等[7]设计了一种基于Polar码的比特交织编码调制系统,当码长较大时,实现相同的误码率,该系统所需的信道信噪比比未经交织调制的系统最大节省0.8 dB。文献[8]提出了一种增强的置信传播(belief propagation,BP)译码算法,采用级联外码的方式提高译码准确率。但是,这些方法以增加复杂度为代价,在短码长Polar码上的应用存在很大的局限性。此时,仅仅通过改进Polar码的译码方法来提高译码准确性是不够的。针对上述问题,引入多天线输入和多天线输出技术(multiple-input multiple-output,MIMO),它采用多天线发送和接收信息,对信息进行整合处理,充分挖掘空间维度资源,从而有效提高通信系统的可靠性[9-11]。
随着机器学习的不断发展,深度神经网络为诸多的研究领域注入了新鲜的血液,并且收获了更准确、更高效的研究成果。文献[12]提出了一种基于深度学习的线性码译码器,优化了BP译码算法的性能。在Polar码译码研究方面,Tobias利用全连接神经网络,创新性地提出了基于深度学习的Polar译码方案[13],并指出深度神经网络通过训练,不仅能对码组进行分类,还可以学习到Polar码的编译码结构,在未经训练的码组上存在泛化的可能。但是,当码长很短时,信道得不到充分的极化,极大地影响了Polar码通信的准确性。然而,为了在5G通信中达到海量机器类通信和超可靠低延时的要求,实现万物联网的目标,又对提高短码长的Polar码性能提出了迫切的、更高的要求。卷积神经网络(convolutional neural network,CNN)[14]用卷积操作代替矩阵相乘操作,能够通过局部感受野更好地提取出二维输入数据中空间信息[15-16],并且通过权值共享的方式减少网络参数数量。因此,利用卷积神经网络能够更好地提取多天线数据特征,提高低信噪比下短码长Polar码的译码准确性。
本文提出了一种基于CNN的多天线(CNN-MIMO)Polar码联合解调-解码方案。利用CNN能够在数据中提取到更多空间信息,学习更深层次、更有区别度的特征信息的优良特性,结合MIMO技术能够充分挖掘无线通信空间维度资源的优势。本系统采用CNN搭建了Polar码的解调-解码网络,利用CNN神经网络,准确而高效地提取不同天线接收到的有噪编码码组之间的关系特征,以及码字内部比特的结构特征,从而改善短码长Polar码在低信噪比情况下误码率高的问题。实验结果表明,本方法具有较高的有效性。
1 系统模型
本文提出的基于卷积神经网络的Polar码联合解调-解码方案模型如图1所示。
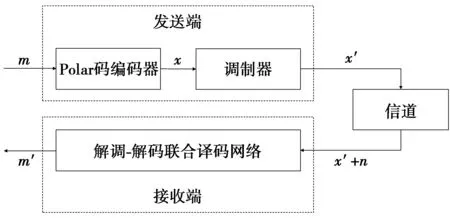
图1 基于卷积神经网络的Polar码的联合解调-解码方案模型Fig.1 Joint demodulation-decoding model of polar codes based on the convolutional neural network
在发送端,对k位原始信息m进行Polar编码得到N位编码比特x。根据信道极化原理,对N=2n个相互独立的信道先合并,再分裂。计算每个信道的巴氏参数,按照巴氏参数值递减的顺序排序。通过这种方法将信道极化成信道容量近似为1和信道容量近似为0的2个部分,分别记为信道集合A和信道集合Ac。在信道集合A中传输信息比特uA,在信道集合Ac中传输固定的冻结比特uAc。码长为N的Polar码编码过程可表示为
⊕uAcGN(Ac)
(1)

2 基于CNN的联合解调-解码网络
2.1 数据集的生成
一般而言,除了利用公共数据集对神经网络进行训练外,生成满足神经网络训练的数据集是一项既费时又费力的工作。但是,当利用神经网络译码时,生成它的训练数据集则不同。可以通过给编码比特xi加上随机噪声nit得到CNN联合解调-解码网络的数据集。它相当于通信系统中,发送端发送的编码信号经过信道,受到噪声的干扰,再到达接收端的大量有噪信息。对k位原始信息m进行编码,得到样本大小为2k的所有可能的编码比特集合X={x1,…,xt,…,x2k} 。其中,xi={b1,…,bi,…,bN},bi∈{0,1}。假设第t次对X中的全部样本进行训练,训练使用的数据为Xt,Xt可以表示为
(2)
训练数据对应的标签集为所有可能的原始信息mi的集合M,M={m1,…,m2k},其中,mi={b1,…,bk}。在训练时,为了提高训练效果需要打乱样本顺序,并且每次送入网络的是X的一个子集Xsub。
测试数据由编译码系统随机产生。假设每一个测试块大小为l,则信源端随机产生的原始测试信息集合Mtest={m1,…,ml}为该测试块对应计算误比特率的测试标签集。一组原始测试信息Mtest经过Polar编码器进行编码,通过信道加入噪声,得到该组测试数据Xtest={x1+n1,…,xl+nl},再输入到基于CNN的Polar码的联合解调-解码网络。
2.2 CNN网络的搭建
为了更好地提取信号的时间特征和空间特征,本文设计了一种基于CNN的联合解调-解码网络架构,如图2所示。整个联合解调-解码译码网络由4个模块组成,分别是输入模块、卷积模块、全连接模块、输出模块。各模块具体设计安排如下。

图2 基于CNN的联合解调-解码网络架构Fig.2 Architecture of CNN based demodulation-decoding joint network
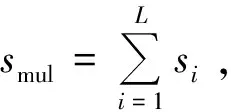
2)CNN模块。CNN模块由4层卷积层组成。利用CNN神经网络的局部感受野和权值共享的特点,先通过卷积运算对多天线接收到的有噪编码比特进行局部比特信息的特征提取,这样的局部卷积可以减少特征抽象过程中的相互依赖,因而降低网络对输入数据样本恶性畸变的敏感性。随着网络层数加深,CNN网络将会在高层网络对低层网络提取到的特征进一步综合学习。此外,CNN卷积神经网络的多核卷积特点还可以保证网络从多角度提取不同特征,以免产生偏见,从而更好地拟合出Polar码的译码函数。
第1层卷积层采用64个Filer,1×1大小的卷积核对输入矩阵进行逐点扫描,提取全面的细节信息。得到64通道N×N的三维输出特征矩阵。CNN神经网络是权值共享的,Filer个数即代表提取的特征个数。
第2层卷积层采用64个Filer,5×5大小的卷积核对第一层的输出矩阵卷积。一方面,由于Polar码的编码核是2×2的,每4个编码比特之间联系紧密,使用5×5的卷积核能在横向上更好地“学习”编码序列内部比特之间的关系/另一方面,5×5的卷积矩阵在纵向上能更多融合多条天线之间的信息,增加译码的可靠性。
第3层卷积层同样采用64个Filer,卷积核大小改为1×5。这样进一步强化对编码比特之间关系的“学习”。
第4层仍然采用64个Filer,5×5大小的卷积核对第3层的输出矩阵卷积。
每个CNN层都采用校正线性单元作为激活函数。Relu的表达函数为
fact=max(0,x)
(3)
此外,对每个卷积层做0.3的dropout,防止过拟合。
3)全连接模块。全连接模块通过全连接层将CNN模块提取到的三维特征矩阵展开,形成一个一维特征序列,起到降低特征维数,提高网络效率的作用。它由2个全连接层构成,分别有1 024个和256个神经元组成。全连接层同样使用relu作为激活函数,做0.5的dropout处理。
4)输出模块。输出模块是一个具有k个神经元的全连接层,k个神经元的输出对应k位比特的原始信息。输出模块使用sigmoid作为激活函数。sigmoid的表达式为
(4)
sigmoid函数起到对二进制相移键控调制解调的作用。通过sigmoid激活函数,每个神经元的输出值将在0到1之间,并且在经过整个译码网络之后,非常逼近0或者1。设阈值为0.001,则大于0.999的输出译为1,小于0.001的输出译为0。
2.3 联合解调-解码网络的学习过程
基于CNN的联合解调-解码网络是利用深度学习卷积前馈神经网络拟合Polar码的译码函数,通过训练译码网络,学习并不断修正权重参数,得到最优译码函数,从而实现Polar码的一次性译码。
定义CNN-MIMO译码网络的输入为s,输出为m′,整个网络的译码函数fPolar_dec可以表示为
(5)
(6)
(7)
(8)
所以,CNN-MIMO译码网络fPolar_dec可以表示为
(9)
针对通信系统信道编译码的特点,定义联合解调-解码网络的损失函数为
(10)

3 实验仿真及分析
为了验证基于CNN的多天线Polar码联合解调-解码方案的性能,在高斯白噪声(additive white gaussian noise,AWGN)信道下对其进行仿真实验。卷积神经网络仿真平台为Ubuntu16.06操作系统,Keras深度学习架构上,选择Theano架构作为后端,并用GPU进行加速。仿真时采用信息比特长度为8bit,选择二进制相移键控(binary phase shift keying, BPSK)的调制方式。
图3为天线数为1时, Polar码译码方案误比特率(bit error rate, BER)性能比较。对比了连续删余译码、置信传播译码、基于全连接层神经网络译码方案与基于CNN的联合解调-解码译码方案在AWGN信道上的BER。其中, Polar码编码码率为1/2,DenseNN和CNN的Polar码译码方案的全部数据的训练次数为5×105次,均对106组polar码进行测试,l=1 000。从图3中可以看出,当使用1 dB信噪比进行训练时,测试信噪比为0~5 dB,基于CNN的Polar码BER都低于其他3种。具体来说,在信噪比为2.5 dB时,基于CNN的BER比SC,BP和DenseNN分别提高了约12.5%,24.7%和40.0%。在信噪比为4.75 dB时,分别提高了约39.3%,47.9%和64.7%。可见,基于CNN的译码方案比SC,BP算法在短码长Polar码译码准确度上有更出色的表现;相对于全连接网络来说,CNN网络能够提取到码组内部比特与比特之间的关系信息,从而提升译码准确度。
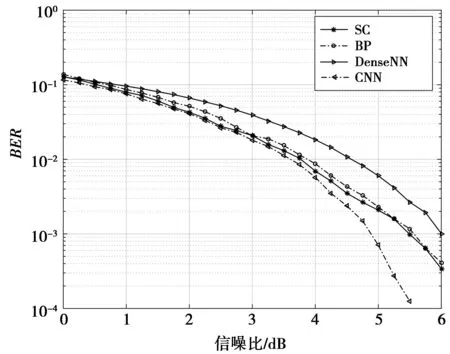
图3 Polar码译码方案误比特率(BER)性能比较Fig.3 Comparison of BER performances between Polar code decoding schemes
图4给出了4天线和8天线Polar码的CNN与Dense译码性能对比图,仿真训练迭代次数均为5×105次,测试polar码组数均为106。
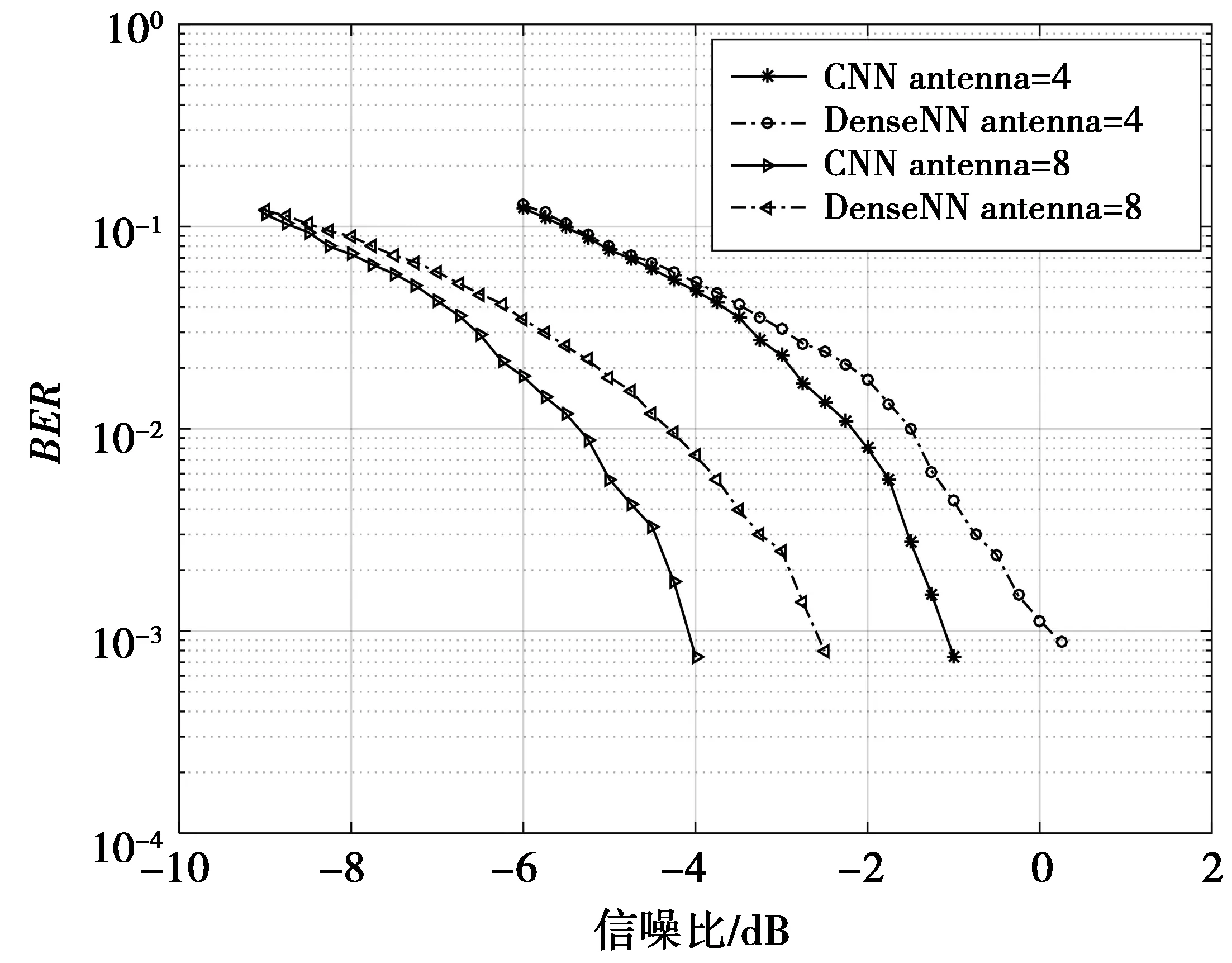
图4 4天线和8天线Polar码CNN与Dense译码性能对比Fig.4 Performance comparison of CNN and Dense decoding schemes for 4 and 8 antenna Polar codes
由图4可知,当天线数为4时,Polar码的误比特率瀑布曲线大幅向低信噪比方向移动。当误码率达到6×10-3时,4天线CNN译码比4天线DenseNN译码约节省1.1 dB;图4中的4天线CNN比图3中单天线CNN译码约节省6 dB。当误码率达到7×10-3时,8天线CNN译码比8天线DenseNN译码约节省2.0 dB;8天线CNN比图3中单天线CNN译码约节省9.0 dB。这是因为基于CNN的多天线译码方案能充分整合学习多天线接收信号之间的空间信息,从而降低误码率。
考虑到一个信道译码系统需要对不同编码码率的Polar码字具有良好的兼容性。本文改变编码码率对CNN与Dense译码系统性能进行验证,采用的Polar码码率分别为1/4和1/8,仿真结果如图5所示。
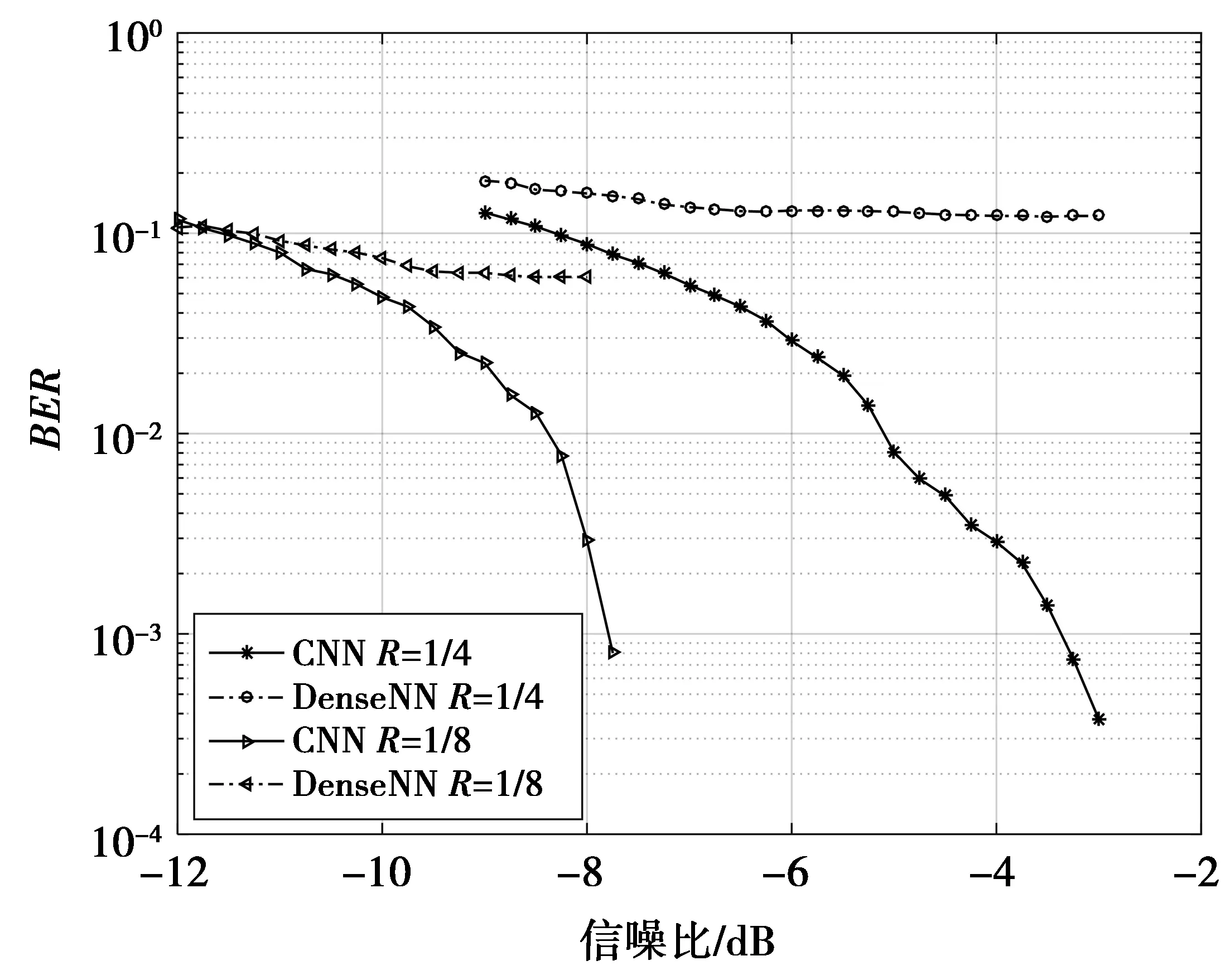
图5 4天线1/4和1/8码率Polar码CNN与Dense译码性能对比Fig.5 Comparisonof 4 antenna Polar codes’ BER performances between CNN and dense decoding with encoding rate 1/4 and 1/8
图5中,随着信噪比的增加,CNN译码系统皆能使不同码率的Polar码的误码率迅速下降,而DenseNN译码系统则不能正常的译码。
究其原因,DenseNN译码系统[13]的神经网络每一层的神经元数量是固定的,当总码长增加时,输入的数据量变大,网络不能正确拟合出译码函数。而CNN译码系统的卷积层的神经元数量不是固定的,它是随着输入数据大小自适应调整的,译码函数的正确性不会受到影响。这样,CNN译码系统便可以兼容不同码率的Polar码。
神经网络的损失函数曲线能够反映系统的“学习”性能。图6将4天线CNN与Dense译码网络的损失函数曲线进行对比,选用1/4和1/8码率的Polar码,分别对2个系统进行6×104个epoch训练。可以看出,CNN译码网络的损失函数曲线迅速收敛到0.05以下且波动起伏较小,而DenseNN网络的损失函数曲线因为网络神经元数量不能随输入数据量大小自适应调节,所以不能收敛到较低值。这也从另一方面证明了基于CNN的多天线Polar码联合解调-解码系统的优越性。
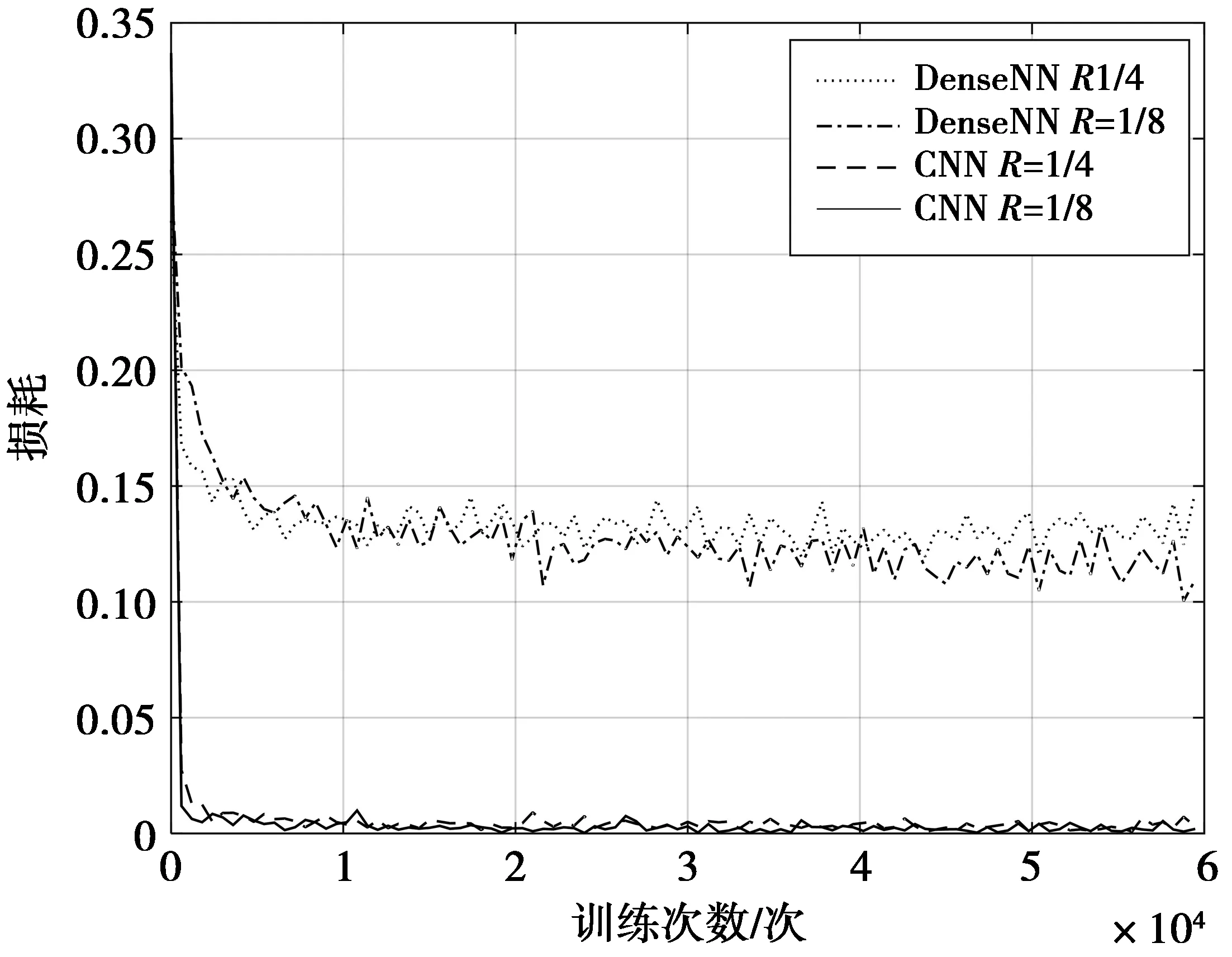
图6 4天线Polar码CNN与Dense的损失函数曲线对比Fig.6 Comparison of 4 antenna Polar code loss values between CNN and dense decoding performance
仿真实验结果表明,基于CNN的多天线Polar码联合解调-解码方案能够有效地拟合出Polar码的译码函数,实现对短码长Polar码的解调、解码,并且在低信噪比情况下,CNN网络的Polar码译码BER相对于DenseNN的译码BER有明显下降。这正是因为本文所提出的Polar码解调-解码网络是针对短码长Polar码编码、译码的特点,选择了合适的CNN神经网络层数、卷积核的大小以及每一层的激活函数和dropout值,既不至于使网络结构过深过大,所囊括的函数库过于庞大,导致网络过拟合,又能根据输入数据大小自适应的学习,使网络所包含的函数库恰好满足拟合出Polar码译码函数的需要,提高了译码网络的准确性和鲁棒性。
4 结论
本文将CNN引入Polar码译码系统,验证了运用CNN神经网络进行信道解码的可行性,并结合多天线技术,实现降低短码长Polar码误比特率的目标。首先生成适用于Polar码译码的训练和测试数据集,搭建了基于CNN的多天线深度学习译码网络,并对网络中的每个模块的具体参数进行设计,提出适合于估计译码网络性能的损失函数。然后,分析了基于CNN的多天线译码方案在BPSK调制,高斯白噪声信道条件下的性能。研究结果表明,基于CNN的译码网络译码准确率高于基于全连接层译码网络的译码准确率;此外,结合多天线技术的CNN译码方案能够明显提高短码长Polar码的译码准确度。因而,本文方案能为未来5G海量机器类通信和超可靠低延时通信提供一种可行的技术储备。
参考文献:
[1] SHANNON C E. A mathematical theory of communication[J]. The Bell System Technical Journal, 1948, 27(3): 379-423.
[2] ARIKAN E. Channel combining and splitting for cutoff rate improvement[J]. IEEE Transactions on Information Theory, 2006, 52(2): 628-639.
[3] ARIKAN E. Channel polarization: A method for constructing capacity-achieving codes for symmetric binary-input memoryless channels[J]. IEEE Transactions on Information Theory, 2009, 55(7): 3051-3073.
[4] ARIKAN E. Systematic polar coding[J]. IEEE Communications Letters, 2011, 15(8): 860-862.
[5] TAL I, VARDY A. List decoding of polar codes[J]. IEEE Transactions on Information Theory, 2015, 61(5): 2213-2226.
[6] NIU Kai, CHEN Kai. CRC-aided decoding of polar codes[J]. IEEE Communications Letters, 2012, 16(10): 1668-1671.
[7] 樊婷婷, 杨维, 许昌龙. 基于Polar码的BICM系统在AWGN信道中的性能[J]. 东南大学学报:自然科学版, 2016(1):18-22.
FAN Tingting,YANG Wei,XU Changlong. Performance of BICM system based on Polar code in AWGN channel[J]. Journal of Southeast University: Natural Science Edition, 2016(1):18-22.
[8] GUO Jin, QIN Minghai, I FABREGAS A G, et al. Enhanced belief propagation decoding of polar codes through concatenation[C]//Information Theory (ISIT), 2014 IEEE International Symposium on. Piscataway, NJ: IEEE, 2014: 2987-2991.
[9] 罗万团, 方旭明, 程梦,等. 高速铁路移动通信系统多天线分集接收方案[J].通信学报,2014,35(6):73-81.
LUO Wantuan,FANG XuMing,CHENG Meng, et al. Multi-antenna diversity receiving scheme for mobile communication system in high-speed railway[J]. Journal of Communication, 2014, 35(6):73-81.
[10] 姚鑫凌, 谢显中, 田瑜. 多小区MIMO网络中一种新的D2D通信干扰对齐算法[J]. 重庆邮电大学学报:自然科学版, 2016, 28(5):641-647.
YAO XinLing,XIE Xianzhong,TIAN Yu. A new interference alignment algorithm for device-to-device communication underlaying multi-cell MIMO networks[J]. Journal of Chongqing University of Posts and Telecommunications: Natural Science Edition, 2016, 28(5):641-647.
[11] 颉满刚, 贾向东, 周猛. 大规模MIMO蜂窝网与D2D混合网络物理层安全性能研究[J]. 重庆邮电大学学报:自然科学版, 2017, 29(1):19-28.
XIE Mangang,JIA Xiangdong,ZHOU Meng. Study on physical layer security of hybrid networks with massive MIMO cellular and device-to-device networks[J]. Journal of Chongqing University of Posts and Telecommunications: Natural Science Edition, 2017, 29(1):19-28.
[12] NACHMANI E, BE’ERY Y, BURSHTEIN D. Learning to decode linear codes using deep learning[C]//Communication,Control,and Computing. Piscataway,NJ: IEEE Press, 2016:341-346.
[13] GRUBER T, CAMMERER S, HOYDIS J, et al. On deep learning-based channel decoding[C]//Information Sciences and Systems (CISS), 2017 5 1st Annual Conference on. Piscataway, NJ: IEEE Press, 2017: 1-6.
[14] LECUN Y, BENGIO Y. Convolutional networks for images, speech, and time series[J]. The Handbook of Brain Theory and Neural Networks,1995,3361(10):255-258.
[15] HOU Yonghong, LI Zhaoyang, WANG Pichao, et al. Skeleton optical spectra based action recognition using convolutional neural networks[J]. IEEE Transactions on Circuits and Systems for Video Technology, 2016(99):1-1.
[16] LI Chuankun, HOU Yonghong, WANG Pichao, et al. Joint Distance Maps Based Action Recognition With Convolutional Neural Networks[J]. IEEE Signal Processing Letters, 2017, 24(5): 624-628.

