Kohn-Sham Density Matrix and the Kernel Energy Method

POLKOSNIK Walter,MASSA Lou

1The Graduate Center of the City University of New York,Physics Department,365 5th Avenue,New York,NY 10016,USA.

2 Hunter College of the City University of New York,Chemistry Department,695 Park Avenue,New York,NY 10065,USA.

3 The Graduate Center of the City University of New York,Physicsand Chemistry Departments,365 5th Avenue,New York,NY 10016,USA.

1 Introduction

In quantum chemisty the computational diきculty of solving the Schrodinger equationincreasesdramatically withthenumber of basis functions1.The computational diきculty of the kernel energy method scalesmoresoftly and hasbeen shown to provide accurate energy results over a wide range of systems at their equilibrium geometries2–9.In the kernel energy method the molecule is cut into subsets called kernels.The KEM energy is defi ned as

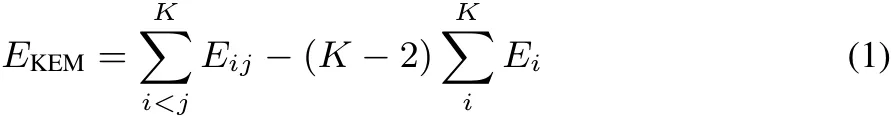
where EKEMis the full molecule energy,Eiand Eijare the energiesof single and double kernels respectively,and K is the total number of single kernels.Double kernels consist of the union of atoms in the single kernels.While KEM is known to generally give energies close to full molecule ab-initio energies it does not deliver the density matrix of the full molecule,nor thecorresponding orbitals.

In this paper we use a generalization of KEM that provides the full molecule KS orbitals and KS density matrix from KS/DFT calculations on individual kernels.The kernel expansion of thedensity matrix is defi ned for the full molecule and then the conditions of idempotency and normalization are imposed on it by an algorithm due to Clinton.The resulting density matrix,because it is factorizable into a product of LCAO coeきcient matrices,maps to a set of full molecule KS orbitals.Those orbitals and density allow calculation of all KS expectation values.In particular,the KS density allows calculation of coherent X-ray scattering structure factors of crystallized molecules.

2 Discussion

Here we review the fundamental ideas related to the use of KEM to obtain a normalized idempotent density matrix from KS/DFT results10.

Thematrix R=C†C isthedensity matrix expressed in the ψbasis.The KEM version of this density matrix is defi ned by analogy to the KEM energy expression.

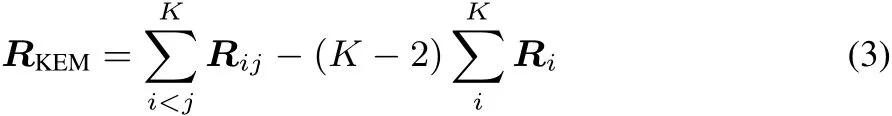
The matrices Riand Rijare constructed from the individual single and double kernel density matrices to represent their contribution to the full molecule density.The KEM density matrix RKEMcontains contributions from all the single and double kernels that constitute the full molecule.The union of the single kernels represents all the atoms in the full molecule.The double kernels include the interactions between all pairs of single kernels.In this way,RKEMis an approximation to the global density matrix for the full molecule. While RKEMis not N-representable,N-representability will beimposed by the Clinton algorithm as decribed below to provide a N-representable global density matrix for thefull system.

Each kernel density matrix must be adapted to the full molecule basis to represent the contribution of that kernel to the full molecule.This is done by augmenting the kernel matrices as we now indicate.

For asinglekernel density matrix,denoted by ri,theform of the corresponding augmented matrix is

where riisthe entiresinglekernel density matrix set asa block into theappropriateposition in a matrix which is the size of the full molecule matrix.

For a double kernel density matrix,rij,the corresponding augmented matrix is of the form

3.1.4 提高气缸套维修质量。保证气缸套的内孔表面粗糙度较高，尺寸精确，保证形状及位置都能够符合位置公差。同时气缸套及机体要有足够的刚度，从而降低气缸套在工作中的变形问题。

where(rij)iiistheblock from thedoublekernel density matrix that corresponds to basis function products for atoms only in kernel i and(rij)jjis the block referring to basis function products for atoms only in kernel j.The oあ-diagonal blocks(rij)ijand(rij)jiare elements of the double kernel density matrix which multiply basis function products from atoms in kernels i and j.The remaining elments of the matrix are set to zero.

The density matrix P is defined in terms of the R density matrix through thesquareroot of theoverlap matrix S.

The overlap matrix S in the full molecule basis is obtained from the single and double kernel matrices through a process similar to the construction of the augmented kernel density matrices.In the case of S,however,the matrix elements from the kernel overlap matrices are simply placed in their appropriate positions.

The normalized projector condition will be imposed by the Clinton equations11.In termsof P,thenormalization condition for double occupied orbitals is tr P=N/2 and the projector condition is P2=P.The Clinton equationsare obtained from extremizing

where tr(P2−P)2= ‖P2− P‖2is the square of the Frobeniusnorm of thediあerencebetween P2and P and λ isa Lagrange multiplier that enforces the normalization constraint.The Clinton equations are

As the iteration number n increases,the Lagrangian multiplier λn,used to impose normalization,goesto zero,and the matrix P goes to a normalized projector.The resulting projector determines a set of full molecule KSorbitals which deliver the KSelectron density12.

3 Results

To illustrate the formalism discussed in the previous section we study a simple proof of concept system consisting of three helium atoms in a linear confi guration symmetric about a plane through the middleatom.Calculations for avariety of distances separating the atoms were done to explore the accuracy of both the KEM energy and theenergy associated with thenormalized projector KS/KEM density matrix.The range of the distances separating theatomswastaken to be0.4RvdW＜R＜2.0 RvdW,where RvdW=1.4Å(1Å=0.1 nm)is the van der Waals radius of helium.At the minimum separation the atoms are heavily clashing.At distances smaller than 0.4RvdWKS/DFT calculations on the double kernels are not possible due to close contacts.The greatest separation used was twice the van der Waalsradiusof helium.Atthisdistanceeach atom isessentially independent of theothersand resultsarenot expected to change appreciably at larger distances.The three single kernels were taken to betheindividual helium atoms,thusthedoublekernels consist of the three pairings of those three single kernels.

Thecalculationsfor theproof of conceptsystem areall based upon the chemical model KS/DFT B3LYP,using STO-3G and 6-31G(d,p)basissets.Resultsfor theenergy and density matrix elements were extracted from the Gaussian program.The KS energy E[P]associated with a given density matrix was also calculated using Gaussian13.

The numerical results for EKEMover the range of distances considered are shown in Table 1 for the STO-3G basis and in Table 3 for the 6-31G(d,p)basis.The energies obtained from the KEM density matrix after imposing normalization and idempotency using the Clinton algorithm are presented in Table2 for the STO-3Gbasis and in Table4 for the6-31G(d,p)basis.In all these tables Efullis the energy of the full system,which is provided as a reference for comparison to the KEM results.

For large R,i.e.R/RvdW＞ 1,Tables 1–4 show that the direct KEM energy,EKEM,and the KEM projector energy,E[Pprojector],are close to the full molecule energy in both the STO-3Gand 6-31G(d,p)basis.Asthedistanceof separation R decreases,however,the direct KEM energy values in the STO-3G basis(Table 1)begin to steadily diverge from the full molecule results while the normalized projector energy(Table 2)is accurate at all distances.At the minimum separation distance of 0.4RvdWthe energy diあerence EKEM− Efullhas risen to a very large magnitude of error, −137kcal·mol−1,while E[Pprojector]− Efull=1.84 × 10−5kcal·mol−1,a very small error.Even at large separations the projector energy is much closer to thefull moleculeenergy.

For calculations on the proof of concept system in the 6-31G(d,p)basis the KEM energy and the KEM projector energy both track the full molecule energy for R/RvdW＞1.In contrast with the results for the STO-3G basis,the straightforward KEM energy and the projector energy bothdiverge from the full molecule energy as the separation between the atoms decreases.Also in contrast with the results in the STO-3Gbasis,in thecases R/RvdW=1.8,1.7,1.4,1.3,0.6,the straightforward KEM energy is more accurate than the projector energy.Theprojector energy in the majority of cases,however,ismoreaccuratethan the KEM energy.

Table 1 KEM energy results,E KEM,compared to full molecule energies E full,both calculated in the STO-3G basis,for thelinear helium system over a range of atomic separations.

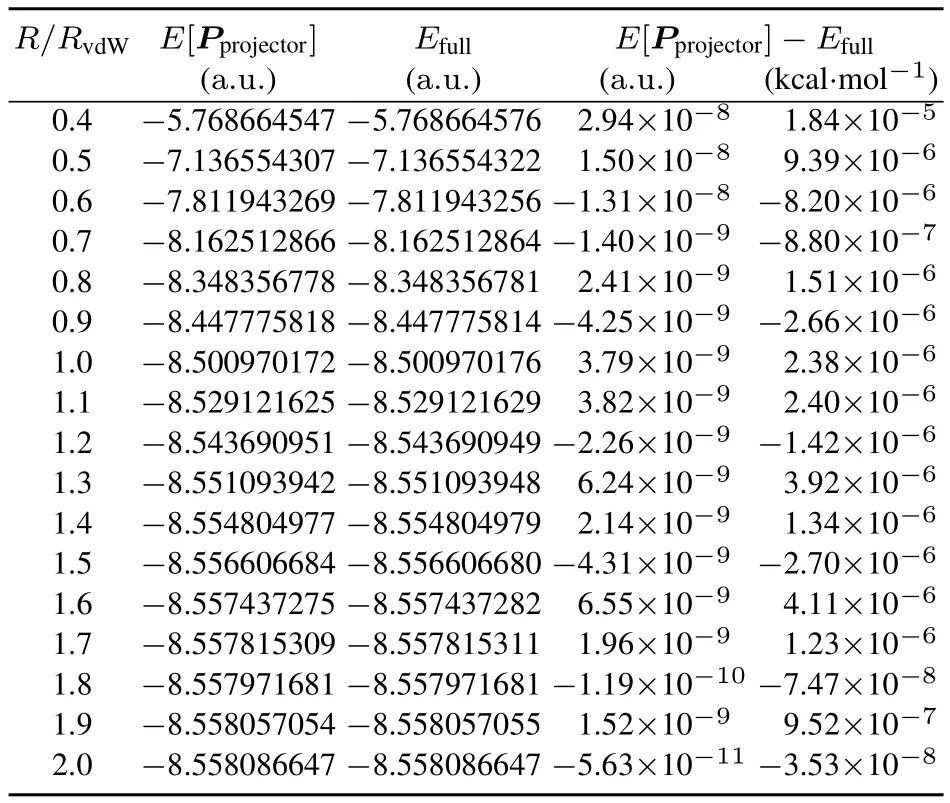
Table2 Projector density matrix energies E[P projector]compared to full molecule energies E full,both calculated in the STO-3G basis,for thelinear helium system over a rangeof atomic separations.

Thetrendswehavedescribed for theproof of concept system in the STO-3G basis are also presented in Fig.1.In Fig.1,for interatomic distances R/RvdW＞1 the KEM energy,EKEMclearly closely tracks the full molecule energy,Efullwhile for R/RvdW＜1,EKEMdiverges from Efull.The energy of the projector,E[Pprojector],isaccurateover thewholerangeof atomic separations.The energy obtained from the KS/KEM density matrix E[Pprojector]is very close to the full system energy evenin the extreme cases for which the atoms are strongly clashing.The KEM information hasbeen transformed into information on the KSorbitals pertaining to the full molecule accurately over thewholerangeof separation distanceswehaveconsidered.

Table3 KEM energy results,E KEM,compared to full molecule energies,E full,both calculated in the6-31G(d,p)basis,for the linear helium system over a rangeof atomic separations.

Fig.1 Diあerencesbetween thefull moleculeand both KEM and projector energiesfor thelinear helium system in the STO-3G basis.

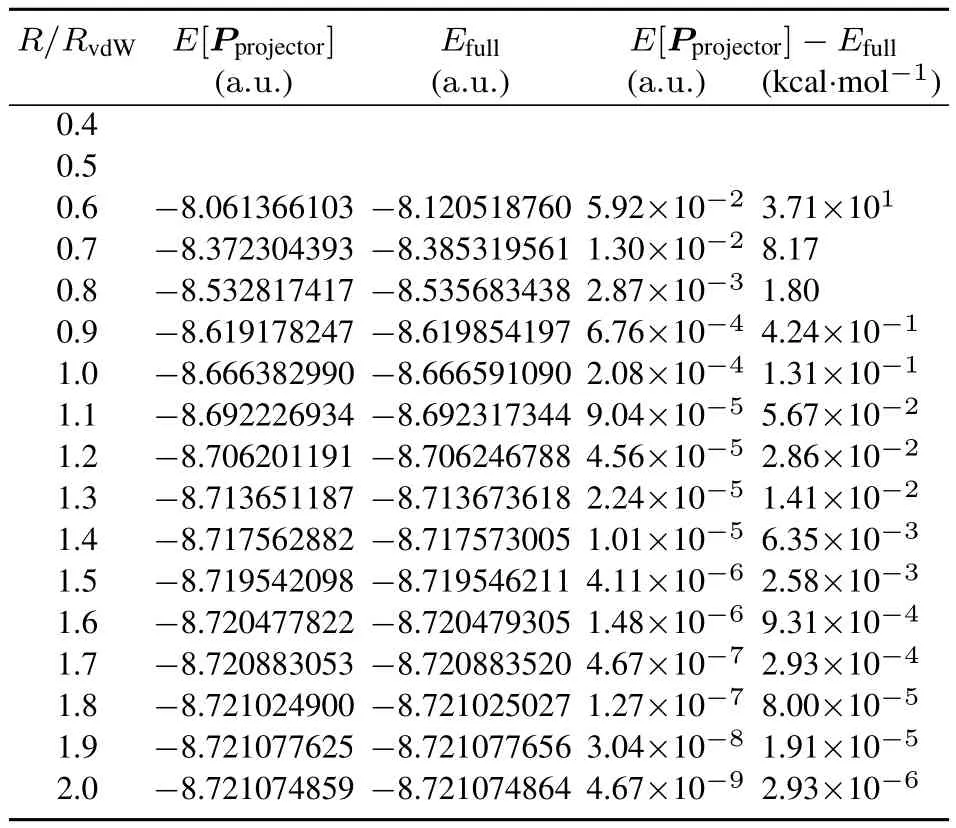
Table4 Projector density matrix energies E[P projector]compared to full moleculeenergies E full,both calculated in the 6-31G(d,p)basis,for thelinear helium system over a rangeof atomic separations.

The results for the 6-31G(d,p)case are presented in Fig.2.Both the KEM and projector energies diverge astheseparation between the atoms decreases,while for physically reaonable separations both the KEM and projector energy give accurate results.

Therearethreeimportant measuresto judgetheconvergence of the Clinton equations.Oneisthemeasureof thequality of the normalizationof P duringtheiterations,tr(Pn)−N/2.Another is the Lagrange multiplier for the normalization constraint,λn.The most important measure is the quality of the projector,as given by the square of the Frobenius norm of the diあerence between P2nand Pn,‖P2n− Pn‖2.Each one of these should decreaseasthenumber of iterations,n,of the Clinton equations increases.

For the STO-3G basis,the Clinton equations converge to a normalized projector for all separations.Detailsof each step of the Clinton algorithm for 0.4RvdWare given in Table 5 along with the energy of the density matrix.The iteration number is denoted by n,with n=0 being the energy of the augmented density matrix sum in Eq.(3).As the iteration number,n increases,the parameters measuring the quality of the normalization,idempotency and normalization constraint converge to very small values even in this case,which is the most clashing.The criterion for convergence of the Clinton algorithm used in this paper was that‖P2− P‖2＜1×10−28.For larger atomic separations for calculations in the STO-3G basis,R＞0.4RvdW,the algorithm converges in fewer iterations.

For the proof of concept system in the 6-31G(d,p)basis the Clintonequationsconvergeato normalized projector in all cases except R/RvdW=0.4,0.5.In the case for R/RvdW=0.4 the measure of the quality of the projector diverges.The initial value is‖P2− P‖2=2.8 which increases to 2.4×106in two steps while the density matrix remain normalized to high precisionateachstep.Our algorithmabandonsfurther iterations when‖P2−P‖2＞ 1.0×106.For the case R/RvdW=0.5 the Clinton algorithm gets caught in a local minimum after eight iterations.It remains at‖P2− P‖2=5.95×10−2with E[P]=−2.75a.u.for theremaining iterations.

The measures of the quality of convergence for each step of the Clinton algorithm for the 0.6RvdW6-31G(d,p)case are given in Table6.Each column reportsthesameparametersasin the STO-3G case in Table 5.For larger atomic separations the algorithm convergesin fewer steps,as in the STO-3G basis.

Fig.2 Diあerencesbetween thefull moleculeand both KEM and projector energiesfor thelinear helium system in the6-31G(d,p)basis.

Table5 Clinton algorithm applied to theinitial P KEM for the linear helium system calculated in the STO-3G basisat an atomic separation of R=0.4 R vd W.

Table6 Clinton algorithm applied to theinitial P KEM for the linear helium system calculated in the6-31G(d,p)basisat an atomic separation of R=0.6 R vd W.

As a test of the KEM/KS procedure for a more chemically interesting system wecalculated the KEM energy and apply the KS/KEM procedureto obtain the KS/KEM density for acluster of twelvewater molecules at an energy minimized geometry14using KSDFTand the6-31G(d,p)basis.Theresultsfor thiscase arepresented in Tables7 and 8.Theconvergenceof the Clinton algorithm to a normalized projector is presented in Table 9.The Clinton equationsconvergerapidly and provideacalculated energy which iscloser to thefull molecule energy by afactor ofnearly four.

Table7 KEM energy resultscompared to full moleculeenergies for thetwelvewater moleculecluster.

Table8 Projector density matrix energiescompared to full moleculeenergiesfor thetwelvewater moleculecluster.

Table9 Clinton algorithm applied to theinitial P kem for the twelvemuleculewater cluster

4 Conclusions

Thisisthefi rst study showing how full molecule KSorbitals can be extracted from KS/KEM calculations. The straightforward kernel energy expansion does not deliver full molecule orbitals.To address this gap in the application of the kernel expansion method to solutions of the KS equations we have shown how to construct an initial full molecule KEM density matrix and how to obtain a normalized projector from this initial matrix using the Clinton equations.The resulting matrix,because it is a projector,is factorizable into a product of matrices R=C†C whose factors C will deliver the full molecule KS molecular orbitalsφ =Cψexpanded in the atomic orbitals.After imposing the projector property upon the density matrix its KS/KEM energy is in the majority of cases closer to that of the full molecule than is the direct KEM energy,as has been shown in the numerical calculations of this paper.

Applied to quantum crystallography15–17,analogously to what has been done here,one may also calculate the KS/DFT quantum mechanics of the kernels composing a molecular crystal.One can then put together the density matrix for entire crystal by properly summing the kernels,at the same time attaching experimental Debeye-Waller factors to the basis functions.The resulting density can then be used to calculate the X-ray scattering factors.The magnitude of the resulting crystallographic R-factor then becomes the measure of the accuracy of the KS/KEM orbitalsof themolecular crystal.This is important to quantum crystallography in as much as it means that true quantum mechanics,including the exact density KS orbitals can be extracted from the X-ray data.

Acknowledgement:This paper is dedicated to the memory of Professor Robert G.Parr to celebrate his contributions to DFT.We thank Douglas Fox and Fernando R.Clemente of Guassian,Inc.for invaluable discussions.We thank CUNY for useof computer resources.

(1)Weiss,S.N.;Huang,L.;Massa,L.J.Comput.Chem.2010,31,2889.doi:10.1002/jcc.21584

(2)Huang,L.;Massa,L.;Karle,J.Biochemistry 2005,44,16747.doi:10.1021/bi051655l

(3)Huang,L.;Massa,L.;Karle,J.Proc.Nat.Acad.Sci.USA 2006,103,1233.doi:10.1073/pnas.0510342103

(4)Huang,L.;Massa,L.;Karle,J.Int.J.Quantum Chem.2005,103,808.doi:10.1002/qua.20542

(5)Huang,L.;Massa,L.;Karle,J.Proc.Nat.Acad.Sci.USA 2005,102,12690.doi:10.1073/pnas.0506378102

(6)Huang,L.;Matta,C.;Massa,L.Struct.Chem.2015,26,1433.doi:10.1007/s11224-015-0661-1

(7)Timm,M.J.;Matta,C.F.;Massa,L.;Huang,L.J.Phys.Chem.A 2014,118,11304.doi:10.1021/jp508490p

(8)Huang,L.;Massa,L.;Matta,C.F.Carbon 2014,76,310.doi:10.1016/j.carbon.2014.04.082

(9)Huang,L.;Bohorquez,H.J.;Matta,C.F.;Massa,L.Int.J.Quantum Chem.2011,111,4150.doi:10.1002/qua.22975

(10)Polkosnik,W.;Massa,L.J.Comput.Chem.2017,doi:10.1002/jcc.25064

(11)Clinton,W.L.;Massa,L.J.Phys.Rev.Lett.1972,29,1363.doi:10.1103/PhysRevLett.29.1363

(12)Löwdin,P.-O.Phys.Rev.1955,97,1474.doi:10.1103/PhysRev.97.1474

(13)Frisch,M.J.;Trucks,G.W.;Schlegel,H.B.;Scuseria,G.E.;Robb,M.A.;Cheeseman,J.R.;Scalmani,G.;Barone,V.;Mennucci,B.;Petersson,G.A.;et al.Gaussian 09,Revision D.01;Gaussian Inc.:Wallingford,CT,USA,2009.

(14)Maheshwary,S.;Patel,N.;Sathyamurthy,N.;Kulkarni,A.D.;Gadre,S.R.J.Phys.Chem.A 2001,105,10525.doi:10.1021/jp013141b

(15)Huang,L.;Massa,L.;Karle,J.;Matta,C.F.Quantum Biochemistry;Wiley-VCH,Verlag GmbH&Co.KGaA:Weinheim,Germany,2010;chap.1.

(16)Grabowsky,S.;Genoni,A.;Bürgi,H.-B.Chem.Sci.2017,8,4159.doi:10.1039/C6SC05504D

(17)Jayatilaka,D.;Gatti,C.;Piero,M.Modern Charge-Density Analysis;Springer:The Netherlands,2012;chap.6.