关键词拍卖中广告位数的事前分析与优化研究

常 瑞,赵 勇,胡二琴,饶从军

(1.华中科技大学系统工程研究所,湖北武汉430074;2.华北水利水电大学电力学院,河南郑州450045;3.武汉理工大学理学院,湖北武汉430070)

1 引 言

拍卖理论是现代经济领域中一个十分引人注目的分支[1−3],而关键词拍卖已成为拍卖领域的重要组成部分.关键词拍卖,又称付费搜索拍卖、位置拍卖等,是搜索引擎运营商出售搜索结果页面上的广告位所采用的一种方式.近十几年来,基于互联网发展起来的关键词广告给搜索引擎带来了无限商机,是搜索引擎运营商的主要收益来源[4].当用户在搜索引擎的搜索框内输入某一关键词时,搜索引擎生成一个结果页面,该页面由自然搜索结果区域和与该关键词有关的广告区域组成,并且广告区域一般出现在自然搜索结果区域的上方或右侧.用户点击关键词广告链接即可进入广告商的产品页面并有可能完成交易,为广告商带来收益.运营商以拍卖的方式出售这些广告位,并根据拍卖机制为广告商的广告分配位置以及确定其支付费用.

搜索结果页面上展示的广告数对运营商的收益有着很重要的影响.目前,主要的搜索引擎如Yahoo!和Google等均在搜索结果页面上设置了有限个广告位,甚至针对某些关键词只设置一个广告位[5].韩国最大的搜索引擎Naver从2010年开始根据不同的关键词事前设置不同的广告位数,并且将其值在拍卖前向广告商发布.与传统关键词拍卖研究中将广告位数视为固定值不同,文献[6,7,14]将广告位数视作内生变量,研究了运营商收益与广告位数间的关系.Kamijo等[6]基于GSP机制(广义第二价格机制)研究发现限制搜索结果页面上的广告位数可提高运营商的收益.Kim等[7]基于GSP机制探讨了最优广告位数的事前设定方法.

另外,一些学者通过实证研究发现:1)搜索用户会被结果页面上的某些广告吸引而不去点击其他广告,这就是说运营商设置的广告位数会影响广告位的点击率,即点击率存在外部效应[8];2)广告位数也会影响广告商的价值,即价值存在负外部效应[9−11].关键词拍卖中广告商的价值是指单次点击给广告商带来的平均价值,受售卖商品的单位利润和转化率两种因素的影响[4].其中,转化率主要是由网站的设计质量、支付的便利程度和产品的吸引力决定的.由于针对同一个关键词的广告商常常提供相似的产品[12,13],所以,一同展示的其他广告会影响某广告产品的吸引力,这就意味着广告商的价值受广告位数的影响.目前,Kim等[7]已将点击率的外部效应引入到关键词拍卖模型中,并指出当新增广告位对原有广告位的点击率有蚕食作用时,最优广告位数应减少.Kanota等[14]也考虑了点击率的外部效应,发现运营商可通过减少广告位数增加收益.而对价值的负外部效应的研究主要集中于考虑该效应对广告商竞价策略的影响,并未涉及最优广告位数.

关于最优广告位数的主要研究[6,7,14]均基于GSP机制,该机制也是目前关键词拍卖中应用最广泛的机制.但是,“讲真话”不是GSP机制的占优策略,这给广告商带来了额外的报价策略管理成本,造成社会福利的损失,也给拍卖系统带来了不稳定[15,16].因此,在Myerson单物品机制设计理论[17]的基础上,很多研究者致力于寻找激励广告商真实报价的最优关键词拍卖机制.例如,文献[18–20]研究了不同的条件和环境下最优关键词拍卖机制的特征,并与GSP和VCG等机制进行了比较.但是这些研究均将广告位数假设为外生变量.

综上所述,目前关键词拍卖中,机制设计理论主要应用于设计最优化运营商收益的真实机制,尚未用于最优广告位数的研究;而现有的关于最优广告位数的研究均基于GSP机制,广告商不会按照其真实价值报价.并且,主要考虑了点击率的外部效应,尚未关注价值的负外部效应对最优广告位数的影响.然而,考虑价值存在负外部效应时,广告位数会影响广告商的价值和报价,进而影响运营商的收益.因此,在最优广告位数的事前设置研究中引入价值的负外部效应有很强的实际价值.鉴于此,本文将该效应引入到关键词拍卖模型中,在激励广告商真实报价前提下,以机制设计理论为基础探讨最优广告位数的事前设置策略.本文分别建立了广告商价值独立于广告位数的基本模型和广告商价值存在负外部效应的扩展模型;其次,以最大化运营商收益为目标,研究了这两个模型中广告位数的事前设定方法,分析了考虑价值的负外部效应对最优广告位数的影响;最后通过数理证明和仿真考察了竞拍人数和点击率对于最优广告位数和运营商收益的影响,以期为运营商如何提高收益提供借鉴.

2 基本假设和相关定义

首先给出如下基本假设:

1)运营商在拍卖前公布广告位的数量为K,N个风险中性的广告商竞争,其中1≤K≤N,且每个广告商只能得到不超过一个广告位.L={1,2,...,N}表示广告商集合,S={1,2,...,K}表示广告位集合;

2)关键词拍卖采用按点击支付(pay for per-click,PPC)模式,即运营商按照点击次数向广告商收取费用,也就是说只有当搜索用户点击了广告链接,广告商才需要付费.这里,广告商的价值表示用户的每次点击为广告商i∈L带来的收益,它与该广告商的广告所处的位置无关;用bi表示该广告商对每次点击的报价.假设广告商价值为私人信息且独立,并服从同一概率分布函数F,对应的概率密度函数为f;

3)搜索结果页面上某一广告的点击率等于广告被点击次数与显示次数之比.假设点击率只与广告所处位置有关,与广告商(广告)无关,且不受广告位数的影响.用θk表示广告位k∈S获得的点击率,并按点击率的大小给广告位编号,使得θ1＞θ2＞···＞θK;

4)价值分布函数和点击率为共同知识.广告商的价值和报价向量分别为v=(v1,v2,...,vN)和b=(b1,b2,...,bN).v−i=(v1,v2,...,vi−1,vi+1,...,vN)表示除了i之外其他广告商的价值向量,f−i(v−i)表示v−i的联合概率密度函数.令T−i=[0,¯v]×[0,¯v]×···×[0,¯v]⊂RN−1表示除了i之外其他广告商价值集合的积.

一个关键词拍卖机制(P,M)由分配规则P和支付规则M 组成.Pik(b)表示报价向量为b时,广告商i∈L得到第k∈S个广告位的概率;Mik(b)表示报价向量为b时,获得第k个广告位的广告商i向运营商提供的单次点击支付.用(v−i,bi)表示其他竞拍者真实披露自己的价值v−i,而广告商i公布自己的报价为bi时的报价向量,此时,广告商i获得的期望点击率为

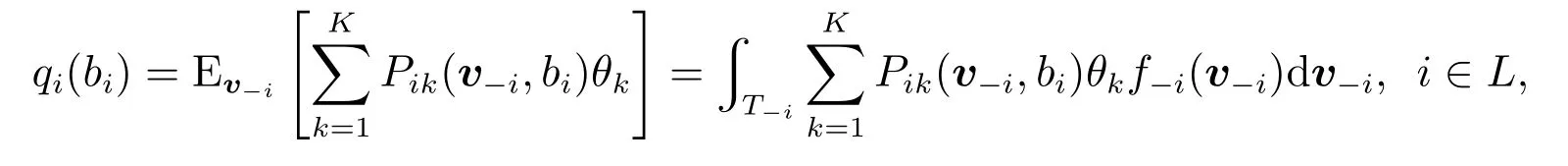
而广告商i的期望支付为

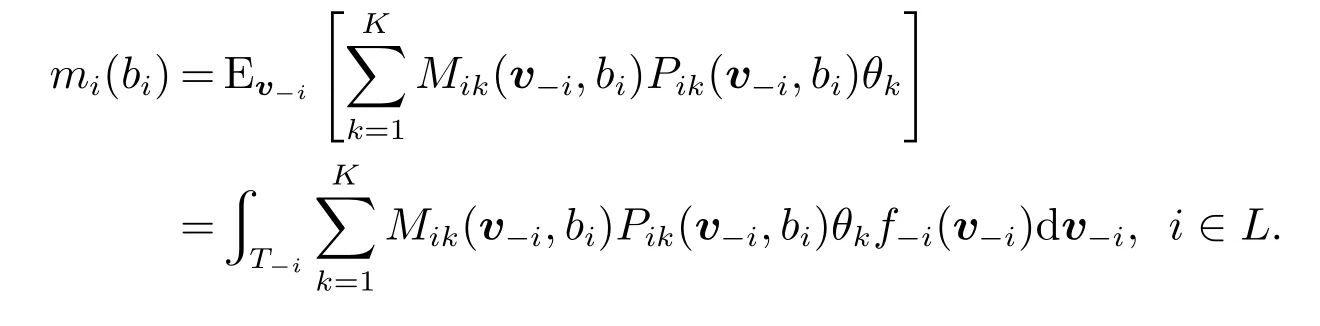
当所有广告商真实报价时,广告商i的期望回报为

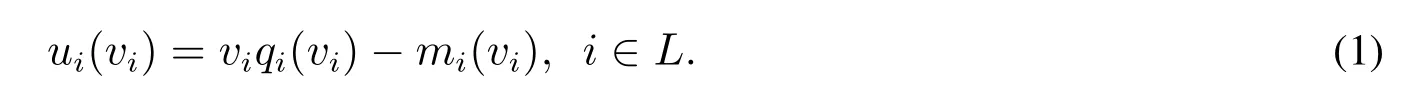
定义1若机制(P,M)满足:

2)(激励相容)在关键词拍卖机制设计中,应保证参与拍卖的广告商i上报真实价值vi时的期望回报不小于谎报价值为bi时的期望收益,即viqi(vi)−mi(vi)≥viqi(bi)−mi(bi),i∈L;

3)(个体理性)在关键词拍卖机制设计中,应保证参与拍卖的广告商i获得非负的期望回报,即ui(vi)≥0,i∈L,则该机制为可行机制.

定义1的条件1)中的第一个不等式表示一个广告商得到广告位的概率非负;第二和第三个不等式意味着每个广告商最多能得到一个广告位以及每个广告位最多能分配给一个广告商.

根据定义1,得到一个可行机制应满足的具体条件.

定理1若一个关键词拍卖机制(P,M)满足下列条件:

1)mi(vi)= −ui(0)+viqi(vi)−是t的非减函数,i∈L,3)ui(0)≥0,i∈L,4)可行性约束,则该机制为可行机制.

证明过程与文献[17]类似,本文不再详述.

3 关键词拍卖模型

3.1 价值独立于广告位数的基本模型

该模型中,假设搜索结果页面上展示的广告数对广告商的价值没有影响.若运营商使用可行机制(P,M),那么广告商的报价等于其价值,即∀i∈L,均有bi=vi.并且,广告商的支付满足定理1中的条件1).所以,广告商i的事先期望支付为

其中表示广告商i的虚拟价值,如果ϕ(vi)是vi的增函数,称机制满足正则性假设.

运营商的事前期望收益为所有竞拍者的期望支付之和,可得

由式(1)有mi(0)=−ui(0),根据激励相容条件应有ui(0)≥0,则mi(0)≤0.而关键词拍卖中广告商的期望支付不可能为负,于是mi(0)=0,因此ui(0)=0.

最优机制设计中,运营商的目标是找到使其收益最大的可行机制(P,M),即

定义排序函数π:N+→ N+,对价值向量v=(v1,v2,...,vN)降序排列,则广告商i的价值在所有的广告商中排在第π(i)位.(v(1),v(2),...,v(N))为排序后的价值向量,有v(1)≥ v(2)≥ ···≥ v(N),其中 v(π(i))=vi.对应的虚拟价值为 (ϕ(v(1)),ϕ(v(2)),...,ϕ(v(N))),如果机制满足正则性,则 ϕ(v(1))≥ϕ(v(2))≥···≥ϕ(v(N)).由式(2)可看出,虚拟价值越大的广告商,分配到点击率越高的位置时,运营商的收益越高.因此,当机制满足正则性假设时,最优化运营商收益的分配规则为:将广告商的价值按降序排列,价值排在第π(i)位的广告商i,若π(i)≤K,获得第π(i)个广告位;否则,得不到广告位.具体表示为

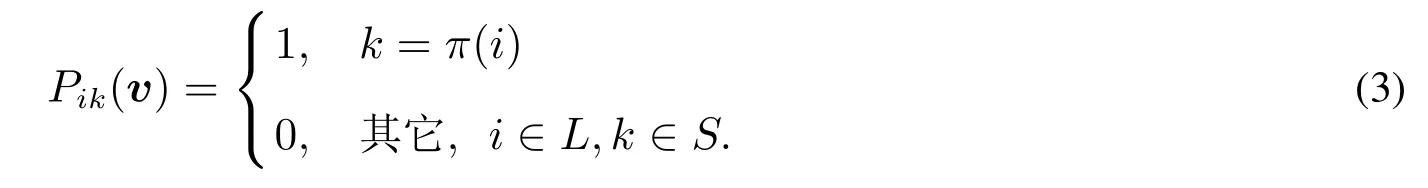
该分配规则与VCG机制的分配规则相同.根据收益等价原理[1],具有相同分配规则的任意两种激励相容机制的期望支付只相差一个常数mi(0).因本文中mi(0)=0,所以,竞拍者在(P,M)机制和VCG机制中的期望支付相同.在VCG机制下,广告商真实报价,其支付等于他对其他广告商造成的效率损失.因此,对于价值排在第π(i)位的竞拍者i,若π(i)≤K,其期望支付为

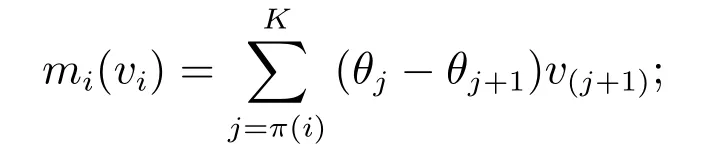
否则,支付为0.所以,机制(P,M)的支付规则满足

在分配规则(3)下,运营商的事前期望收益为

其中分别表示当样本容量为N时,第k高价值及其对应的虚拟价值.

为了便于表达,令则

显然,点击率固定的前提下,当参与拍卖的人数确定之后,式(5)中运营商的收益受到广告位数的影响.当运营商需事前设定广告位数时,其面临的决策问题表示为

式(6)是基于广告商的价值独立于广告位数的假设得到的,称之为基本模型.

3.2 价值存在负外部效应的扩展模型

由于针对同一关键词的广告商常常代表一个行业,因此搜索结果页面上一起展示的广告产品往往具有相似性和可替代性.即使一个用户在决定购买物品前会点击页面上所有的广告,即广告位数不影响点击率,产品的可替代性仍可能导致用户在其他广告中完成交易.也就是说结果页面上的广告数越多,某广告位对应产品的转化率越低,这就意味着广告商的单次点击价值越低.所以,广告位数会影响广告商的价值,即价值存在负外部效应[9,10].

引入一个定义域为[1,N],值域为(0,1]且二阶可导的函数g(x)来刻画价值的负外部效应,并且该函数还具有下列性质g(1)=1,g′(x)＜0,g′′(x)≤0.显然,g(x)为凹函数,称g(x)为负效应函数.

本文假设点击率不受广告位数的影响,以及针对同一个关键词竞价的所有广告商的负效应函数相同且为共同知识.考虑价值的负外部效应,当运营商事前宣布设置的广告位数为K时,广告商i的价值为vig(K).所以,根据负效应函数的性质,可知广告商的价值随广告位数的增加而减小且减小速度变快.假设运营商采用的可行机制为其中表示分配规则,表示支付规则.用来表示竞拍者i获得的期望点击率,而表示其期望支付.竞拍者i的期望回报为

通过与基本模型相似的推导过程,可以得到运营商的事前期望收益

因此,在机制正则的情况下,最优化运营商收益的分配方式与基本模型相同,仍然是将价值按照降序排列,价值排在前K位的广告商依次获得第1到第K个广告位.

该机制下,获得第k个广告位的广告商i向运营商提供的单次点击支付可表示如下

运营商事前决定供应的广告位数,其决策模型为

决策问题(9)表明将广告商价值的负外部效应引入到基本模型中,即为扩展模型.

4 广告位数事前优化分析

根据建立的基本模型和扩展模型,讨论最优广告位数的确定方法,比较分析价值的负外部效应对最优广告位数的影响,并考察点击率对最优广告位数和运营商收益的影响.

4.1 基本模型中广告位数优化研究

根据式(6),基本模型中最优广告位数为定义边际收益为广告位数从K−1增加到K时运营商的收益增量,则其中K ∈L.

引理1[6]在正则性假设下是j的减函数,其中j∈L.

命题1在正则性假设下,边际收益递减.

证明由引理1有又因θK＞θK+1,所以即边际收益是广告位数的单调减函数.证毕.

边际收益随着广告位数单调递减时,运营商可通过增加广告位数至边际收益为零时获得最大收益.因此,可得到如下结论.

定理2基本模型中,最优广告位数值唯一.竞拍人数为N时,若则最优广告位数L∗=N;否则,最优广告位数表示的整数部分,其中¯L满足

证明由命题1,边际收益单调递减,则存在唯一的最优广告位值.若表示当广告位数从N−1增加到N时,边际收益则最优广告位数L∗=N.如果而所以由引理1有＜0.那么,＜0.这就意味着当广告位数从L∗−1增加到L∗时,运营商收益非减;当广告位数从L∗增加到L∗+1,运营商收益减少.因此,当广告位数为L∗时,运营商收益最大. 证毕.

下面进一步分析竞拍者人数对运营商收益的影响.假设广告商人数为W 和M,并且M ＞W,对应的最优广告数分别为运营商的收益分别为

命题2运营商的收益是竞拍人数的增函数.

证明首先,证明

当时,根据定理2有因M ＞ W,由文献[6]可知是N 的增函数,所以有故由引理1有

当时,有则因此,即所以

当时,显然有证毕.

根据式(6),是N的增函数,故由定理2可知,当所以即参加拍卖的人数越多,运营商的收益越大.

竞拍人数的增加使得供应商提供的广告位数增加,顾客点击新的广告也会为运营商带来利润.同时,也会加剧广告商间的竞争,激励广告商提高报价,因此运营商在原有广告位上的收益会增大.所以,样本容量的增大会提高运营商的收益.命题2意味着运营商可通过招募更多的广告商参加拍卖来增加收入,这与直觉上的判断是一致的.

4.2 扩展模型中广告位数优化研究

根据式(9),最优广告位数为

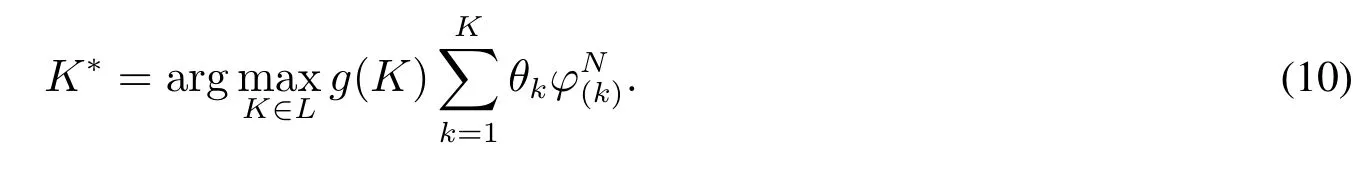
广告位数从K−1增加到K时,扩展模型中运营商的收益增量即边际收益ΔK满足

运营商提供的广告位数从K−1增加到K时,原K−1个位置上的广告商因价值受到新增广告位的影响会降低报价,从而导致运营商在这些广告位上的收益下降.若新增的第K个广告位上广告商的虚拟价值大于零,则运营商的收益增加,否则将会降低.

命题3扩展模型中最优广告位数不超过基本模型中的值,即K∗≤L∗.

证明当L∗=N 时,显然有K∗≤L∗;当L∗＜N 时,根据定理2,有

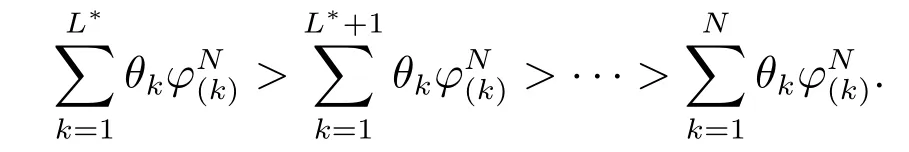
所以,可得

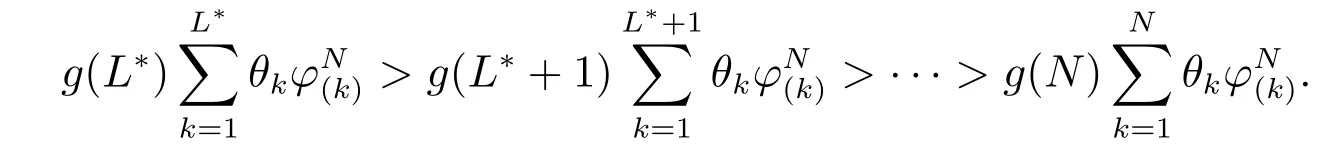
这就意味着,当事前设置的广告位数K＞L∗时,扩展模型中运营商收益是K的减函数.因此,最优广告位数K∗≤L∗. 证毕.

在扩展模型中,若K＞L∗,当广告位数从K−1增加到K时,除了运营商在原来广告位上的收益减少,新增广告位上广告商的期望虚拟价值小于零也对运营商的收益产生了负影响,故运营商的收益降低.因此,与基本模型相比,考虑价值的负外部效应后运营商应提供更少的广告位.所以,在实际中,将该效应引入拍卖模型对于运营商设置更合理的广告位数是至关重要的.该结论与文献[7]中的结论相似.因此,不论考虑价值或点击率的负外部效应,运营商均应设置更少的广告位.本文与文献[7]的结论可为运营商设置合理的广告位数提供理论指导.

在命题3的基础上,考察边际收益ΔK的单调性,易得到如下结论.

命题4负效应函数为凹函数时,边际收益ΔK单调递减,其中K∈{1,2,...,L∗}.

证明由式(11)有

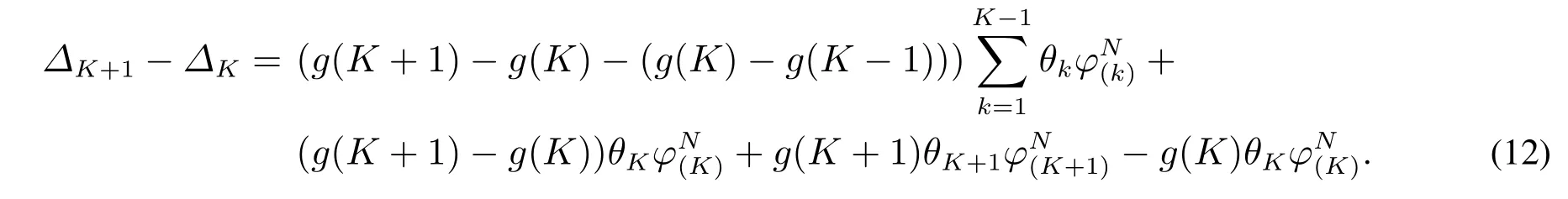
根据g′(x)＜ 0以及g′′(x)≤ 0,其中x ∈ [1,N],而K ≤ L∗≤ N,因此

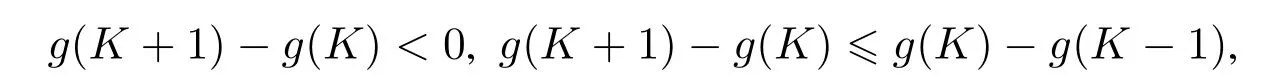
并且由定理2可知,当K ∈{1,2,...,L∗}时,有所以式(12)中等号右侧第一项和第二项均小于等于零.因 g(K+1)＜ g(K),有因此,有ΔK+1−ΔK＜0. 证毕.

根据命题4,扩展模型中边际收益单调递减.因此当边际收益为零时,运营商收益最大,据此可确定最优广告位数.

定理3扩展模型中,最优广告位数值唯一.对于∀K ∈{1,2,...,L∗},若ΔK≥0,ΔK+1＜0,则最优广告位数K∗=K.

证明由命题4可知,扩展模型中,边际收益单调递减,所以存在唯一的最优广告位数值.ΔK≥0,ΔK+1＜0,表示将广告位数从K−1增加到K时运营商收益增加,但是从K增加到K+1时,运营商收益降低,因此最优广告位数为K∗=K. 证毕.

推论1如果g(2)≤1,最优广告位数K∗=1.

证明由引理1和式(11)有

即Δ2＜0.这意味着广告位数由1增加到2时运营商收益减少,所以K∗=1. 证毕.

从推论1可以看出,当第2个广告位与第,或广告商价值受广告位数的影响较严重时,新增加的第2个广告位给运营商带来的收益将不足以补偿第1个广告位上的广告商因价值的负外部效应而降低报价所导致的收益损失.此种情况下,运营商应只设置1个广告位.

实际中,搜索引擎如Yahoo!,Google,Bing等结果页面上的广告数一般为个位数,并且针对某一些关键词仅设置一个广告位.这里,除太多广告会影响客户的体验之外,本文也从另一个角度解释了该现象.

4.3 点击率与最优广告位数和运营商收益的关系分析

基本模型中,运营商的收益是点击率的增函数,且由定理2易知,最优广告位数不受点击率的影响.但是,在扩展模型中,由定理3和式(11)可知,点击率影响最优广告位数的值.实际中,搜索引擎会重点突出某些广告位,文献[6]针对该策略提出了一个简化形式,称之为广告位k–加强(k–accentuation)策略.该策略中,点击率改变的方式为:保持其他广告位的点击率不变,∀k=1,2,...,K∗,增大第k个广告位的点击率至θk+η＜θk−1.假设点击率改变前扩展模型的最优广告位数和运营商的最大期望收益分别表示为K∗和R.而基于k–加强策略改变点击率时,假设边际收益用表示,其中K=1,2,...,K∗,对应的最优广告位数和最大期望收益分别为和Rk.下面分析该策略对最优广告位数和运营商收益的影响.

命题5扩展模型中,对于∀k=1,2,...,K∗,基于k–加强策略改变点击率时,

1)当k∈{1,2,...,K∗−1}时,第k个广告位上点击率的增加使得最优广告位数非增,有K∗;第K∗个广告位上点击率的增加不影响最优广告位数,即

2)k值越小,k–加强策略对应的最优广告位数越少,有

3)运营商的收益增加,且有R1＞R2＞···＞RK∗＞R,即运营商在广告位1–加强策略下的收益最大.

证明当点击率的变化遵循k–加强策略时,易证明边际收益ΔkK递减,因此仍可用定理3来判断最优广告位数.

1)根据式(11),对于∀k=1,2,...,K∗−1,有以及由定理3有所以

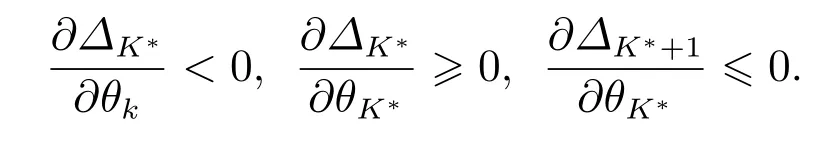
＜ 0表示ΔK∗是点击率 θk的减函数.因此有可能存在η,当 θk增至 θk+η＜ θk−1时,使得这就说明在k−加强策略下,最优广告位数可能减少,即根据式(11)边际收益为

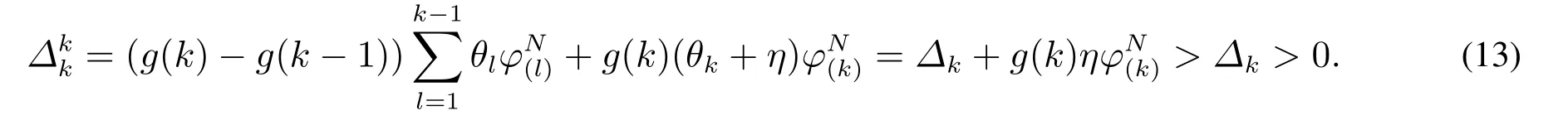
式(13)中第一个不等号成立的原因为,当k＜K∗时因此第二个不等号成立的原因为,根据命题4,当k＜K∗时,广告位k上的边际收益Δk＞ΔK∗≥0.而意味着k–加强策略下最优广告位数所以,对于∀k=1,2,...,K∗−1,有

此外,ΔK∗随着点击率θK∗的增大而增加,而ΔK∗+1却是θK∗的减函数,因此当第K∗个广告位的点击率增加时,仍然有ΔK∗≥0,ΔK∗+1＜0.所以,最优广告位数不变,即

2)点击率变化采用k–加强策略时,对应的最优广告位数为此时有以及对于∀k=2,3,...,K∗,当点击率变化遵循(k−1)–加强策略时,根据式(11)有

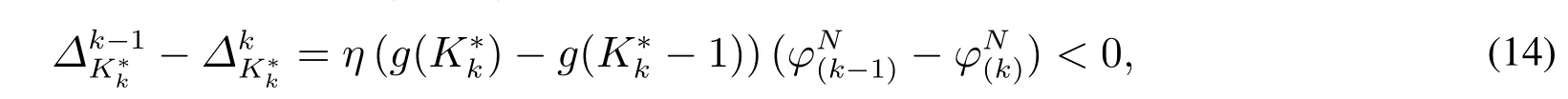
这就意味着所以

式(15)和式(16)表明,在广告位(k−1)–加强策略下,当广告位数从增加到时,运营商的收益可能会降低;当广告位数从增加到时,运营商的收益肯定减少.因此(k−1)–加强策略对应的最优广告位数这就说明对原点击率越高的广告位采取广告位加强策略时,最优广告位数受到的影响越大,即最优广告位数减少的越多.

3)在广告位k–加强策略下,其中k∈{1,2,...,K∗−1},运营商在设定广告位数为最优值时,可获得最大收益Rk,因此有

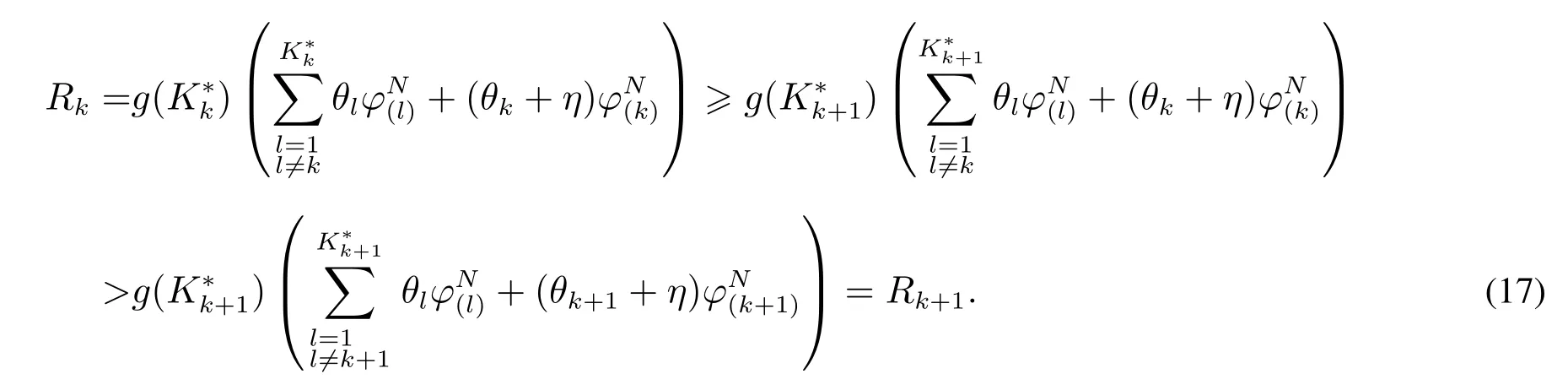
在广告位K∗–加强策略下,运营商的最大收益为RK∗,有

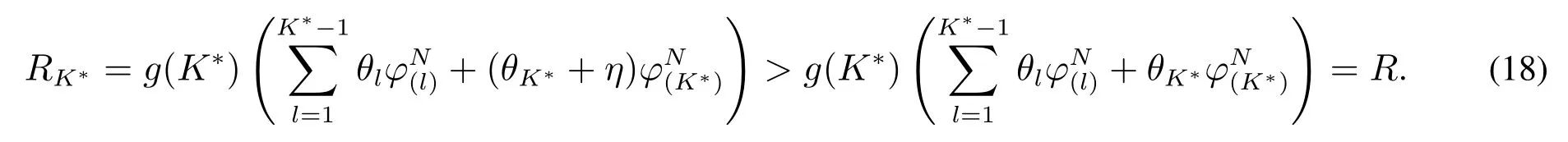
根据式(17)和式(18),有R1＞R2＞···＞RK∗＞R. 证毕.

扩展模型中,k–加强策略主要从三个方面影响运营商的收益:首先,广告位数的减少会导致运营商的收益损失;其次,广告位数的减少使价值存在负外部效应的广告商提高报价,运营商收益增加;此外,运营商的收益也因第k个广告位点击率的增加而提高,并且提高程度与k有关.因k值越小,对应广告位上的点击率和广告商的报价越高.所以,在点击率增量相同的情况下,对原点击率较高的广告位实施加强策略带来的收益增量足以平衡因失去更多广告位而导致的收益损失.因此,按照k–加强策略改变点击率时,k值越小,运营商应提供越少的广告位,却可获得更大的收益.该结论可为实际中运营商重点突出某些广告位的策略提供决策支持.另外,广告位1–加强策略下运营商有可能仅提供一个广告位,这与推论1的结论一致.

5 计算与仿真研究

扩展模型中,竞拍人数也会影响最优广告位数以及运营商的收益.具体地,假设广告商人数为W和M,并且M＞W时,对应最优广告数分别为K∗W和K∗M,运营商的收益分别为RW和RM.首先假设有

根据定理3,当所以式(19)中第二项非负;故式(19)中第一项正负未知.因此,无法判断RW和RM的大小.同理,也可证明当时,仍无法确定RW和RM的大小关系.所以,扩展模型中,竞拍人数对于运营商收益的影响规律难以严格确定,下面拟借助仿真方法进行探讨.另外,扩展模型中最优广告位数不但与竞拍者人数有关,还与负效应函数有关.因此,本文将在负效应函数中引入一指标来表征广告位数对广告商价值的影响程度,在仿真中通过改变该系数来分析价值的负外部效应与最优广告位数和运营商收益的关系.

具体仿真参数设置如下:

1)设负效应函数g(x,δ)=1−((x−1)/N)1/δ,其中x ∈ [1,N].易知,对∀δ∈ (0,1],有g(1,δ)=1,满足3.2节中对负效应函数的要求.另外,即当 δ→ 0时,广告商的价值不受广告位数的影响;并且,当δ∈(0,1]时,有这意味着广告位数固定时,δ越大,广告商的价值受到广告位数的影响越大.所以参数δ可来用表示广告位数对广告商价值的影响程度,称之为负效应系数.在仿真中,通过在区间(0,1]改变系数δ,考察其对最优广告位数和运营商收益的影响规律;

2)根据文献[21],2002年∼2003年Overture的数据表明,参与某一个流行关键词的竞价人数一般都大于等于10.随着近年来互联网行业的发展,目前对高附加值关键词竞价的广告商人数肯定会大大增加.为了使仿真更具说服力,本文将参与某一关键词竞价的广告商人数上限设置为153,并假设至少有3人参与竞价;

3)最优广告位数和运营商的收益均与价值分布函数有关,故在仿真中选取电子商务中常用的三种价值分布函数.在这些分布函数下,分别考察竞拍者人数和负效应系数对运营商收益和最优广告位数的影响规律.根据文献[7],假设广告商价值服从:[0,10]上的均匀分布;[0,∞)上参数为1的指数分布;[1,∞)上的Pareto分布,概率分布函数为F(v)=1−v−2.显然,这三种分布下,虚拟价值均为价值的增函数,即满足本文要求的正则条件;

4)Feng等[18]通过对2003年Overture前五位广告位的实际点击数据分析得出,实际广告位的点击率可用等比数列Θ={0.70,0.71,0.72,...,0.7k−1,...,0.7K−1}来模拟.

点击率保持固定的前提下,扩展模型中最优广告位数和运营商的收益主要受负效应系数和广告商人数等两个因素的影响.这里,仿真考虑两种情况:负效应系数固定,竞拍人数变化;竞拍人数固定,负效应系数变化.下面,在三种价值分布下,分别探讨这两种情况中最优广告位数和运营商收益的变化规律.

1)固定负效应系数δ=0.5.广告商人数以增量2从3增加到153时,三种价值分布下最优广告位数和运营商收益随竞拍人数变化的关系曲线如图1和图2所示.可以看出,三种价值分布下,最优广告位数和运营商的收益都是竞拍人数的增函数.

增加竞拍者人数,意味着广告商对于广告位的竞争加剧而提高报价,运营商的收益增加;因广告商价值存在负外部效应,增加广告位又会导致其报价降低,故运营商收益减少.但是,当竞拍者人数逐渐增加到某一值时,人数的增加对收益的正影响可以抵消广告位的增加对收益的负效应,此时运营商可通过增加广告位获得更高的收益.所以,竞拍人数在一定范围内增加时,最优广告位数保持不变;但是当广告商人数超过某一个值后,最优广告位数将增加.因此竞拍者人数变化时,最优广告位数的变化曲线为多阶梯形,如图1所示.

图1 竞拍者人数与最优广告位数的关系Fig.1 The relationship between the number of bidders and the optimal number of advertising slots

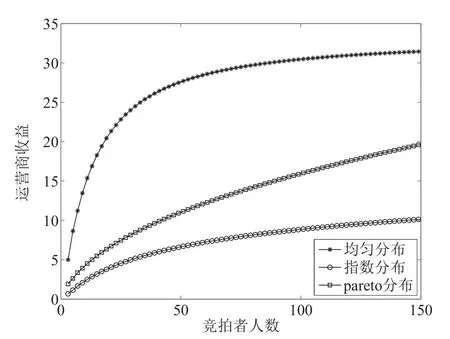
图2 竞拍者人数与运营商收益的关系Fig.2 The relationship between the number of bidders and the operator revenue

增加广告商人数至最优广告位数改变之前,广告位数对广告商价值的影响不变,但是增加竞拍人数使得广告商的报价提高,因此运营商的收益逐渐增加.当竞拍者人数超过某一个值时,最优广告位数增加,新增的广告位给运营商带来了利润,此时竞拍人数和广告位的增加对收益的正效应大于增加广告位对收益的负影响,运营商的收益也会增加.所以,运营商收益是竞拍人数的增函数,如图2所示.这意味着运营商可通过吸引更多的广告商参与拍卖来获得更高的利润.

2)固定竞拍人数N=50.负效应系数在区间(0,1]以增量0.05变化时,三种价值分布下最优广告位数和运营商收益与负效应系数的关系如图3和图4所示.由图可知,最优广告位数和运营商的利润均是负效应系数的减函数.

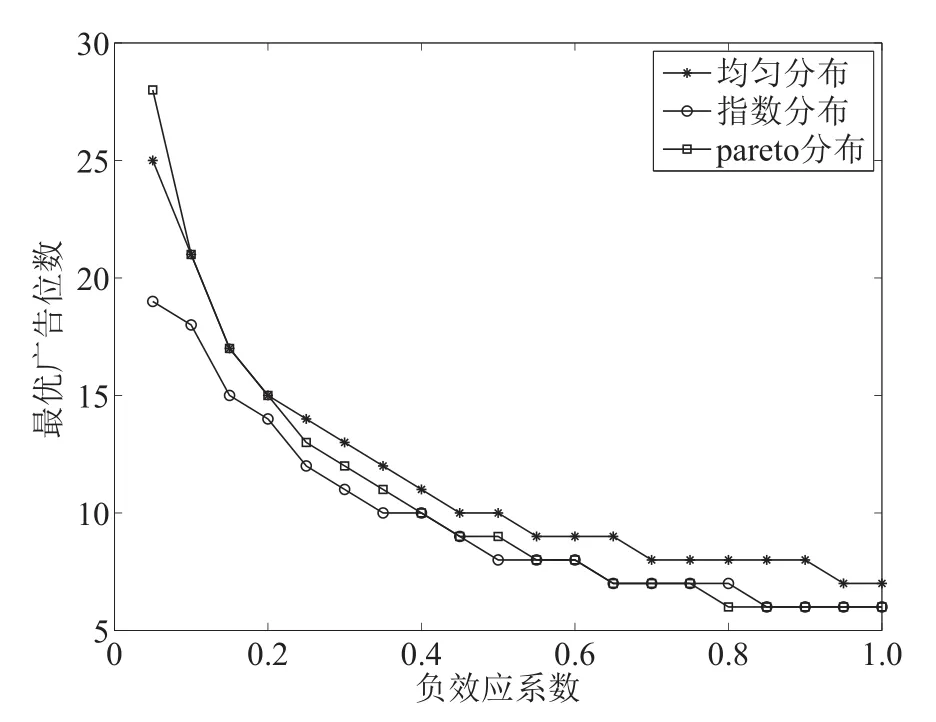
图3 负效应系数与最优广告位数的关系Fig.3 The relationship between the negative effect coefficients and the optimal number of advertising slots

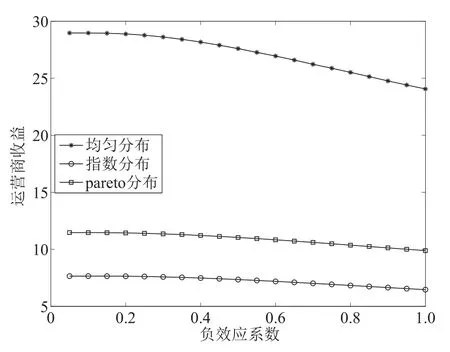
图4 负效应系数与运营商收益的关系Fig.4 The relationship between the negative effect coefficients and the operator revenue

当负效应系数增加时,广告商价值受到的影响变大,报价降低,导致运营商收益降低,但是此时保持原来的广告位数仍然可以使运营商收益最优.当负效应系数超过到某一个值时,运营商可通过减少广告位数来弱化价值的负外部效应对其收益的影响.因此,在一定范围内增加负效应系数时,广告位数会保持不变;但是当该系数超过某一值时,广告位数会减少,如图3所示.

增加负效应系数时,在最优广告位数变化前,因广告商报价降低导致运营商收益减少;减少最优广告位数虽可减弱负效应系数的增加对价值的影响,但是广告位数的减少却意味着运营商获得收益的来源减少,运营商的收益仍然降低,如图4所示.

6 结束语

与传统文献中将广告位数视作外生变量不同,在考虑运营商拍卖前宣布广告位数的情形下,以最大化运营商的收益为目标,研究了广告位数的设定策略.基于机制设计理论,根据不考虑和考虑广告位数对广告商价值的影响,分别建立了基本模型和扩展模型.经分析,发现两个模型中边际收益均为广告位数的减函数,这就说明运营商可通过设置适当的广告位数得到最大收益.进一步,对比分析了两个模型中点击率对最优广告位数的影响规律.可知基本模型中最优广告位数与点击率无关,但是扩展模型中当某一广告位的点击率增加时,运营商应减少广告位.另外,分析还指出两个模型中运营商均可通过招募更多的竞拍者来提高收益.由于考虑了广告位数会影响广告商价值的实际情况,使得本文的结论贴近现实中运营商的决策行为.因此,研究可为运营商的决策提供参考.

需要指出的是,文中假设广告位数对所有广告商价值的影响是相同的,实际中该假设较为严苛.对广告商价值的负外部效应进行深化细化,将是下一步的研究方向．

[1]维佳·克里斯纳.拍卖理论.北京:中国人民大学出版社,2010.Krishna V.Auction Theory.Beijing:China Renmin University Press,2010.(in Chinese)

[2]丁黎黎,王晓玲,徐寅峰.质量门槛约束下的碳排放权拍卖机制研究.系统工程学报,2015,30(5):628–635.Ding L L,Wang X L,Xu Y F.Research on auction mechanism of carbon emissions permits with quality thresholds.Jounal of Systems Engineering,2015,30(5):628–635.(in Chinese)

[3]洪宗友,汪定伟.多属性招标拍卖中买卖双方的最优策略研究.系统工程学报,2014,29(4):458–467.Hong Z Y,Wang D W.Optimal strategies of auctioneer and bidders in multi-attribute procurement auctions.Jounal of Systems Engineering,2014,29(4):458–467.(in Chinese)

[4]刘树林,戎文晋.搜索引擎广告的机制设计理论与实践.北京:科学出版社,2010.Liu S L,Rong W J.Mechanism Design Theory and Practice of Search Engines Advertising.Beijing:Science Press,2010.(in Chinese)

[5]Jerath K,Sayedi A.Exclusive Display in Sponsored Search Advertising.Pittsburgh:Carnegie Mellon University,2015.

[6]Kamijo Y,Adachi T.Optimal Slot Restriction and Slot Supply Strategy in a Keyword Auction.Tokyo:Waseda Institute,2011.

[7]Kim A,Balachander S,Kannan K.On the optimal number of advertising slots in a generalized second-price auction.Mark Lett,2012,23(3):851–868.

[8]Kempe D,Mahdian M.A cascade model for externalities in sponsored search//Proceedings of the 4th International Workshop on Internet and Network Economics.Berlin,Heidelberg:Springer,2008:585–596.

[9]Das A,Giotis I,Karlin A R,Mathieu C.On the effects of competing advertisements in keyword auctions.http://www.cs.upc.edu/igiotis/externalities.pdf,2008.

[10]Ghosh A,Sayedi A.Expressive auctions for externalities in online advertising//Proceedings of the 19th International Conference on World Wide Web.New York:ACM,2010:371–380.

[11]Constantin F,Rao M,Huang C C,et al.On expressing value externalities in position auctions//Proceedings of the Twenty-fifth AAAI Conference on Artificial Intelligence.Menlo Park:AAAI Press,2011.

[12]Jeziorski P,Segal I.What makes them click:Empirical analysis of consumer demand for search advertising.American Economic Journal:Microeconomics,2015,7(4):24–53.

[13]Ayanso A,Karimi A.The moderating effects of keyword competition on the determinants of ad position in sponsored search advertising.Decision Support Systems Science,2015,70(1):42–59.

[14]Katona Z,Sarvary M.The race for sponsored links:Bidding patterns for search advertising.Marketing Science,2010,29(2):199–215.

[15]Edelman B,Ostrovsky M,Schwarz M.Internet advertising and the generalized second price auction:Selling billions of dollars worth of keywords.The American Economic Review,2007,97(1):242–259.

[16]Varian H R.Position auctions.International Journal of Industrial Organization,2007,25(6):1163–1178.

[17]Myerson R B.Optimal auction design.Mathematics of Operations Research,1981,6(1):58–73.

[18]Garg D,Narahari Y.An optimal mechanism for sponsored search auctions on the web and comparison with other mechanisms.IEEE Transactions on Automation Science and Engineering,2009,6(4):641–657.

[19]Feng J,Bhargava H K,Pennock D M.Implementing sponsored search in web search engines:Computational evaluation of alternative mechanisms.INFORMS Journal on Computing,2007,19(1):137–148.

[20]Li J,Liu D,Liu S L.Optimal keyword auctions for optimal user experiences.Decision Support Systems,2013,56(6):450–461.

[21]Edelman B,Ostrovsky M.Strategic bidder behavior in sponsored search auctions.Decision Support Systems,2007,43(1):192–198.