基于节能的地铁时刻表随机机会约束规划模型

杨 荟,周建栋,李 想

(北京化工大学经济管理学院,北京100029)

1 引 言

随着我国城市化进程的不断推进,人们对省时高效,安全便捷的交通出行工具的需求不断增加.地铁作为现代化城市公共交通系统的重要组成部分,相比于其他交通形式(如公交车,出租车等),具有准时性高,载客量大,发车频率和集约化程度高的特性,逐渐成为人们出行方式的首选.然而,地铁运营在满足高运营效率和安全性要求的同时,供电需求和耗电量也在大幅增加.据资料显示,2012年北京地铁系统总耗电量超过10亿kW·h,其中列车牵引能耗占总耗电量的70%左右[1].据《中国城市轨道交通年度报告》课题组和中国土木工程学会城市轨道交通技术工作委员会初步统计,截至2015年底我国内地有25个城市建成并运营110条城市轨道交通线路,运营总里程达3 293 km.随着城市地铁网络的快速扩展,高能源消耗带来的高运行成本问题将越来越严重.无论是从满足可持续发展要求还是减轻地铁运营成本的角度出发,地铁节能优化都势在必行.再生制动是将列车制动过程中的动能转换成电能并提供给处于同一供电站的其他列车加速的一种能量回收技术.在确保地铁运营安全性和服务水平的前提下,通过充分利用再生制动技术对地铁时刻表进行优化,从而提高再生能量的利用率,成为实现地铁节能运行的主要途径之一.也成为时刻表优化问题的另一目的.

目前,国内外关于列车再生能量利用的研究,主要包括运行控制策略优化和时刻表优化两个方面[2].在列车运行控制策略优化研究中,Gordon等[3]和Chen等[4]从再生能量存储的角度出发,研究了基于地铁能耗最小化的列车运行控制方法.Li等[5]提出了地铁系统的动态调度和控制策略,并构建凸优化模型以提高地铁节能性能.

在时刻表优化研究中,周剑斌等[6]基于广州地铁1号线的真实运营数据提出一种新的时刻表编制方法,通过实行该时刻表可使每列列车日平均用电节约0.95 W·h.颜邦杰等[7]兼顾运营成本和服务水平,通过调整行车预留时间得到地铁节能时刻表,并在文章最后给出了地铁节能运行的相关建议.Ramos等[8]通过建立混合整数规划模型对同一供电区间内列车的加速和制动时间进行协调,从而达到提高再生能量利用率的目的.Peña-Alcaraz等[9]以最大化加速列车和制动列车间的重叠时间为目标建立数学规划模型,实验结果表明该最优时刻表不仅能够有效地节约能耗,而且不会对乘客服务质量和投资成本造成消极影响.Yang等[10]考虑更多的现实因素(如:真实速度曲线,供电系统结构等)并在此基础上提出一种新的节能调度方法.该方法通过调整列车的停站时间可使能耗年均降低6.97%.考虑均匀的发车间隔,步兵等[11]从节能运行的角度出发,将单车节能运行和多车协调运行进行统一规划,构建以最小化总能耗为目标的时刻表优化模型.Yang等[12]以最大化重叠时间为目标建立整数规划模型,通过优化停站时间和固定的发车间隔可使早高峰和晚高峰时段的重叠时间分别提高22.06%和15.19%.Li等[13]和Yang等[14]均对速度曲线进行了优化,并以降低能耗为目标建立了时刻表优化模型.Albrecht等[15,16]肯定了Li等[13]提出的一体化节能优化方法,并指出调整繁忙线路的停站时间可显著提高再生能量利用率.Xu等[17]首先对站间的乘客流量变化进行分析并对乘客等待时间进行定义,进而建立了以最小化乘客等待时间和最小化能量消耗为目标的双目标时刻表优化模型.此外,Li等[18]将站间运行时间作为随机变量,基于传统动力学方程所描述的速度曲线建立了以最大化再生能量利用值的期望值为目标的随机时刻表优化模型.

传统研究大多基于动力学方程描述列车的站间运动轨迹.然而列车在实际运行过程中受线路状况、机车条件、电力供应及人为操作等因素的影响,动力学方程无法准确地描述其在站间的真实行为.因此,为了更加贴合地铁运行的实际情形,本文运用真实运动轨迹数据替代动力学方程描述的速度曲线,提出基于数据驱动构建模型的方法.另外,由于列车的发车间隔与再生能量利用之间存在潜在关系,合理选择发车间隔也成为地铁时刻表节能优化问题的主要优化途径之一.因此,本文还研究了非均匀发车间隔的时刻表对再生能量利用的影响问题.采用随机变量的乐观值测度对不同延迟情形下再生能量利用值进行数学描述,以确保含有随机参数的约束条件以一定的置信水平成立,从而建立了基于数据驱动的地铁节能时刻表随机机会约束规划模型.考虑到所建模型含有较多的决策变量,且目标函数和约束条件的构成较复杂,运用传统优化方法进行求解将耗费大量计算时间,难以满足地铁时刻表优化的敏捷性要求,因此本文采用“优化过程设计科学,全局寻优能力强,能够适应大规模多峰优化问题且计算耗费时间合理”的猴群智能算法对模型进行了求解.结果表明基于本模型的地铁运营时刻表可使早高峰和晚高峰时段的再生能量利用量乐观值显著提高.与北京地铁亦庄线现行时刻表相比,通过优化非均匀的发车间隔可至少提高再生能量利用量8.44%.

2 随机机会约束规划模型的建立

2.1 基础知识

为了求解含有随机变量的数学规划问题,Charnes等[19]在1959年首次提出了机会约束规划的概念,其核心思想是确保含有随机参数的约束条件以一定的置信水平成立.本节重点介绍由Liu[20]给出的maximax型机会约束规划模型.

先介绍随机变量的乐观值的定义.

定义1若ξ是一个随机变量,且α∈(0,1],则ξ的α−乐观值定义为

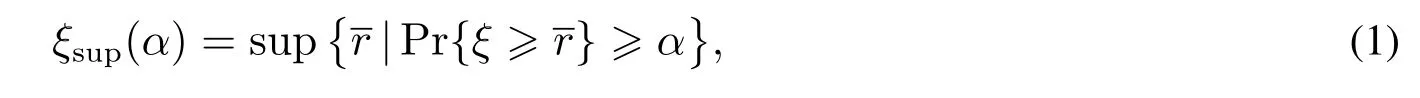
其中Pr为概率测度.

从定义1可知随机变量ξ至少以概率α大于或等于ξsup(α),也即α−乐观值是满足条件的的最大值.

设x是一个决策向量,ξ是一个随机向量,f(x,ξ),gj(x,ξ),j=1,2,...,p分别是含有随机参数的目标函数与约束函数.若决策者希望最大化目标函数的α−乐观值,可构建如下maximax型机会约束规划模型

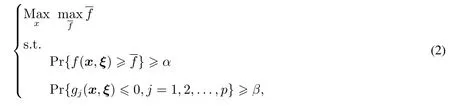
其中是目标函数f(x,ξ)的α−乐观值.

随机机会约束规划模型的求解方法主要分为两类,第一类是分析目标函数和约束函数的确定表达式,进而将其转化为确定的等价模型进行求解.在大多数情况下,由于随机机会约束规划模型中的函数具有不确定性,其近似表达式往往很难得到,因此这一类方法不具有广泛的应用性.第二类方法是将神经网络,Monte Carlo模拟和启发式算法相结合对原模型进行求解,该方法也称之为混合智能算法[21].典型的启发式算法包括遗传算法[21,22],粒子群算法[23−25],猴群算法[26]等.

2.2 模型建立

当前地铁供电大多采用单边供电的模式.在该模式下,电能在不同供电区间内无法传递,并且上行和下行的供电是相互独立的.如图1所示,列车3再生的电能不能用于列车4的加速,列车1和列车2之间的能量无法互相传递.相反,如果某列车处于牵引阶段时,恰好有另一辆同行列车位于同一供电区间且处于制动阶段,那么重叠时间内制动列车再生的电能就可以供给牵引列车用于加速.如图2所示为同一供电区间内两辆连续列车在站间运行的速度曲线,图中,列车i正在加速离开j站,同一变电区间内的另一列车i+1正在制动进入j站,此时阴影部分代表的就是再生电能被利用的重叠时间部分.为了提高再生能量的利用率,本文的目标就是最大化牵引列车和制动列车的重叠时间,使得更多的再生能量得以被牵引列车利用,从而降低列车运行的整体能耗.文中所用参数及符号见表1.

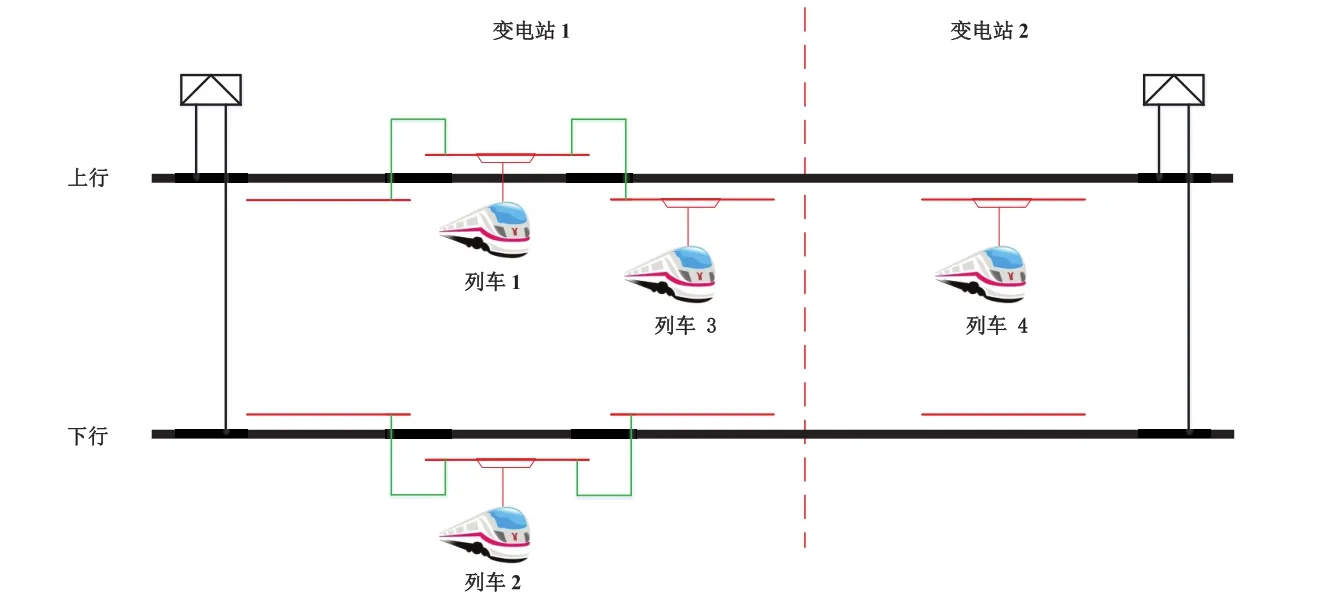
图1 供电系统结构示意图Fig.1 The illustration on power supply system

图2 同一供电区间内两辆连续列车间的速度–时间分布图Fig.2 Speed-time profile of two successive trains within a substation

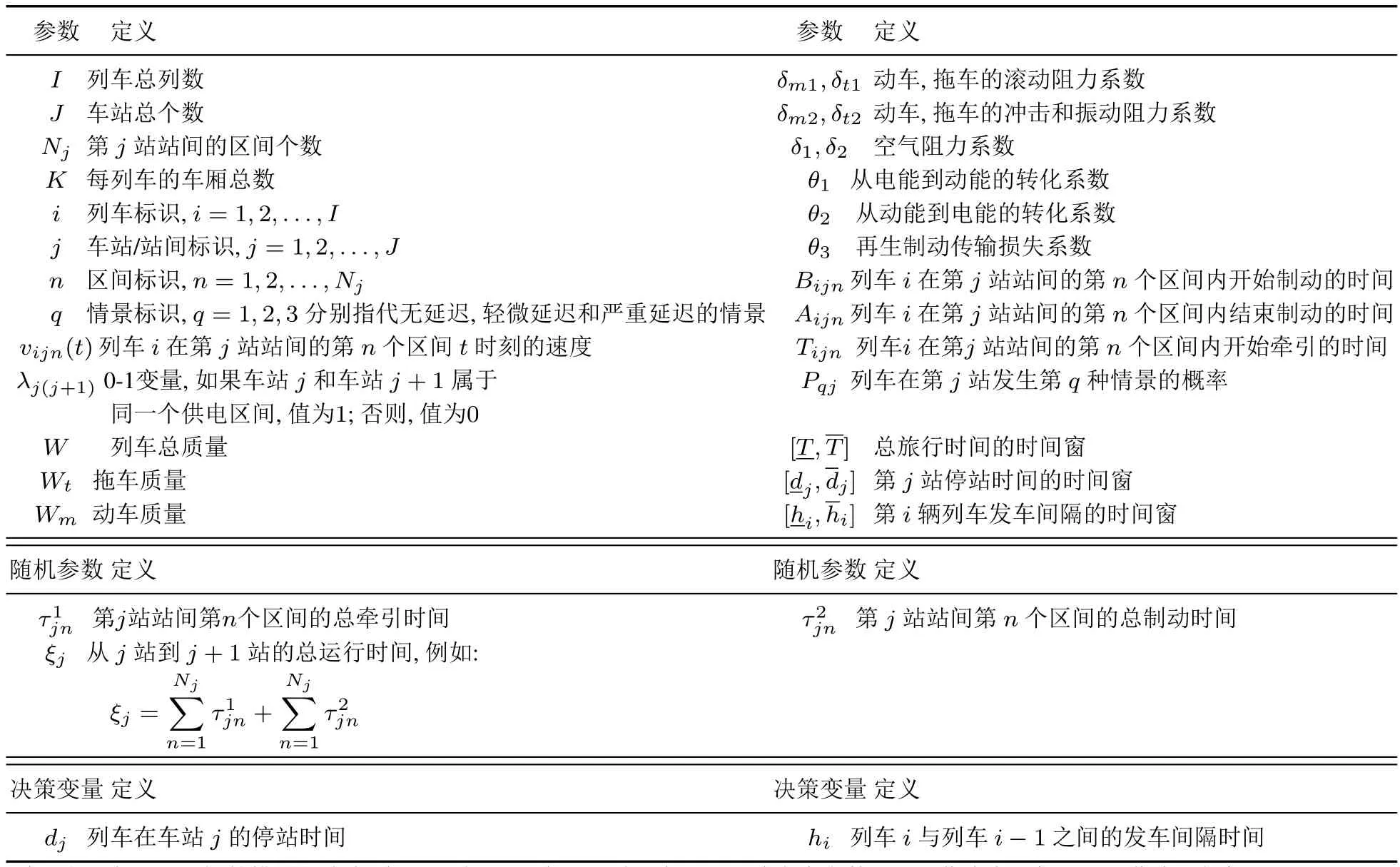
表1 符号系统Table 1 Symbol system

通常将列车的运行轨迹分为加速,巡航,惰行和制动四个工况[13].由于人为操纵因素和外界因素的影响,在列车行驶过程中加速,巡航和惰行工况是频繁交替出现的.然而在对再生能量利用值进行计算时,再生能量的收集仅来源于制动工况,再生能量的利用主要来源于加速工况,巡航和惰行工况极少涉及.因此,将复杂的工况交替过程按四个工况进行逐一划分是没有必要的,并且还会增加运算的复杂度和计算时间,不符合地铁时刻表优化的敏捷性要求.因此,本文将只包含加速,巡航和惰行工况交替出现的运行阶段称为牵引阶段,将制动工况出现的运行阶段称为制动阶段.并以制动阶段结束时刻为结点对站间的运动轨迹进行划分,使每个站间由若干个连续的区间构成,并且每个区间由一个牵引阶段和一个制动阶段构成,以图2为例,列车i在站间j的运动轨迹划分为区间1和区间2,其中,斜纹代表列车处于加速工况,黑色代表列车处于巡航或惰行工况,斜纹和黑色部分合起来称为牵引阶段,波点代表列车处于制动工况,也即制动阶段,并且每个区间都由一个牵引阶段和一个制动阶段组成.

2.3 数据驱动

列车在实际运行过程中往往受线路状况,机车条件及人为因素等影响,动力学方程不能准确地描述其运动轨迹的这一变化特点.以北京地铁亦庄线荣昌东路–同济南路站间为例,图3(a)和图3(b)分别展示了由传统动力学方程描述的速度曲线

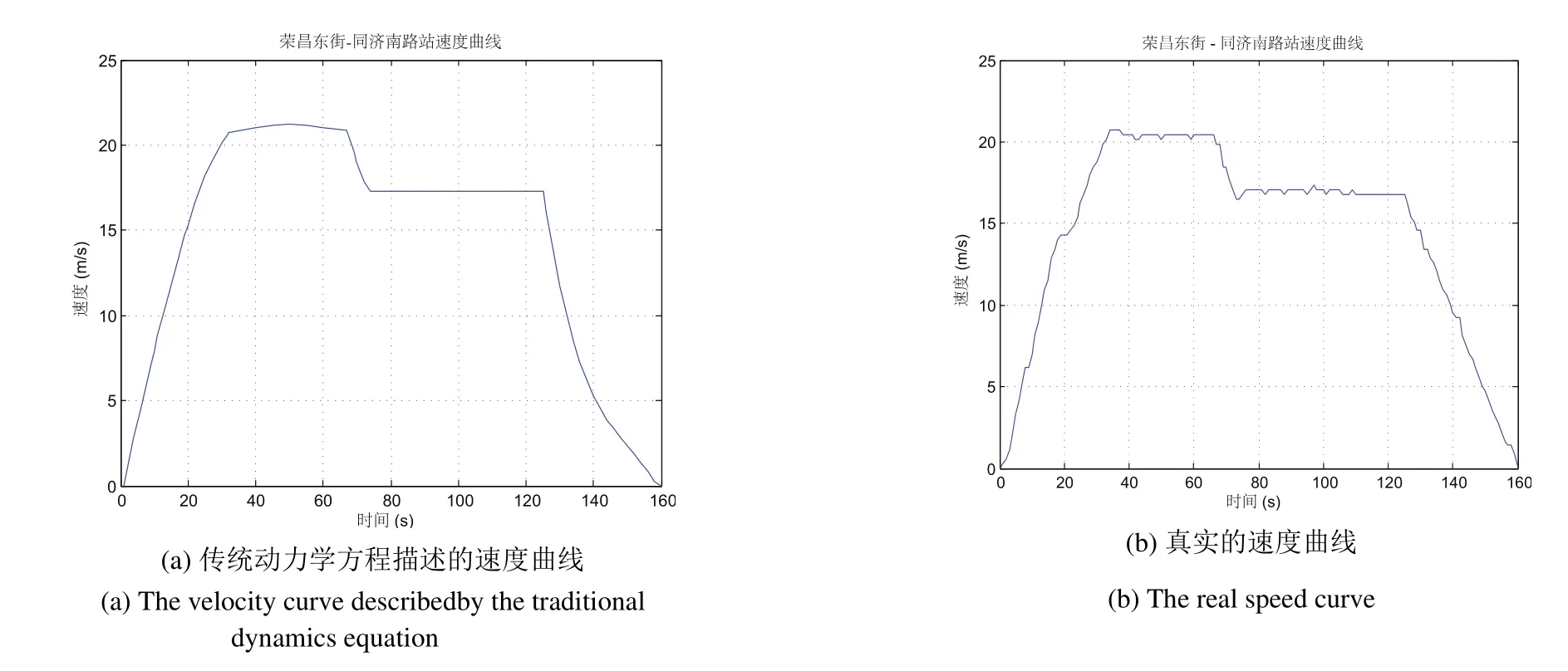
图3 传统动力学方程所描述速度曲线和真实速度曲线对比图Fig.3 Comparison chart of speed profile described by traditional motion equation and real-life data

和真实的速度曲线.因此,为了使得所建模型可靠性高并且具有现实意义,本文基于数据驱动构建地铁时刻表优化模型,用真实的速度数据取代动力学方程描述的速度曲线.

2.4 非均匀发车间隔

地铁运营公司通常为列车分配均匀的发车间隔.实际上,列车的发车间隔与再生能量利用之间存在潜在关系.因此,优化非均匀的发车间隔也是提高再生能量利用率的途径之一.并且,随着优化能力与运算速度的提升,实现列车发车间隔的实时调整也成为了必然趋势.综合以上因素,为了尽可能地提高再生能量利用率,本文考虑非均匀的发车间隔.

2.5 延迟分析

在地铁的实际运营过程中,地铁时刻表常常会受到乘客客流量增大等因素的影响而发生延迟.为了尽可能避免延迟现象的出现,地铁运营公司通常会对站间运行时间进行调节,从而缩小与既定时刻表的差距.本文考虑三种不同的延迟情景,分别为无延迟,轻微延迟和严重延迟,并用pqj(q=1,2,3)分别表示它们在各站间的发生概率.在每种情景下,地铁运营公司将分别制定相应的站间运行策略和列车需要遵循的速度曲线.由于延迟情况的出现是随机的,从而导致不同策略的选择是随机的.因此,分别给出不同情景下第j站站间的第n个区间的牵引时间和制动时间的表达式为

2.6 目标函数分析

在地铁系统中,每辆列车均由动车和拖车车厢编制而成,本文给出列车运行所受阻力的公式[27]如下

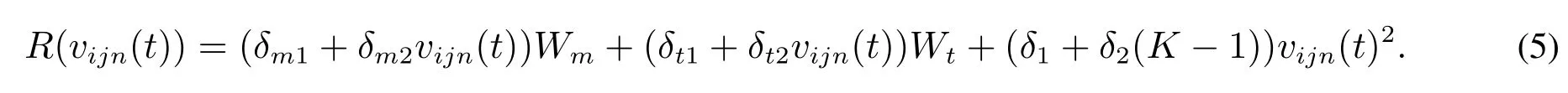
定义决策变量 X=(h1,h2,...,hI,d1,d2,...,dI−1),随机向量 ξ =(ξ1,ξ2,...ξJ−1),其中 hi为每辆列车的发车间隔,dj为每站的停站时间,ξj是随机变量,i=1,2,...,I;j=1,2,...,J−1.当列车离开j站,即n=1时,定义列车在各站的出发时间为

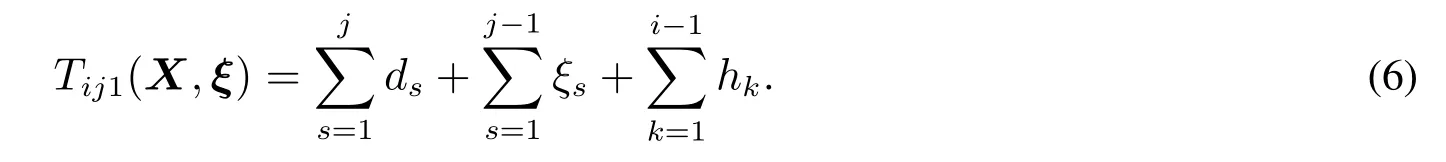
假设第1辆列车从0时刻出发,那么第i辆列车经过了i−1个发车间隔,并且经过了前j−1个站的运行时间和前j个站的停站时间后,从第j站出发.因此,当n=1时,式(5)表示列车i在第j站的出发时间;当n=2,3,...,Nj时,Tijn(X,ξ)表示列车i在第j站站间的第n个区间开始牵引的时间.不难发现,列车i在第j站站间的第n个区间开始牵引的时间与列车i在第j站站间的第n−1个区间结束制动的时间相同.进而,可以给出列车在区间n开始制动,结束制动,以及在下一区间开始牵引的时间为

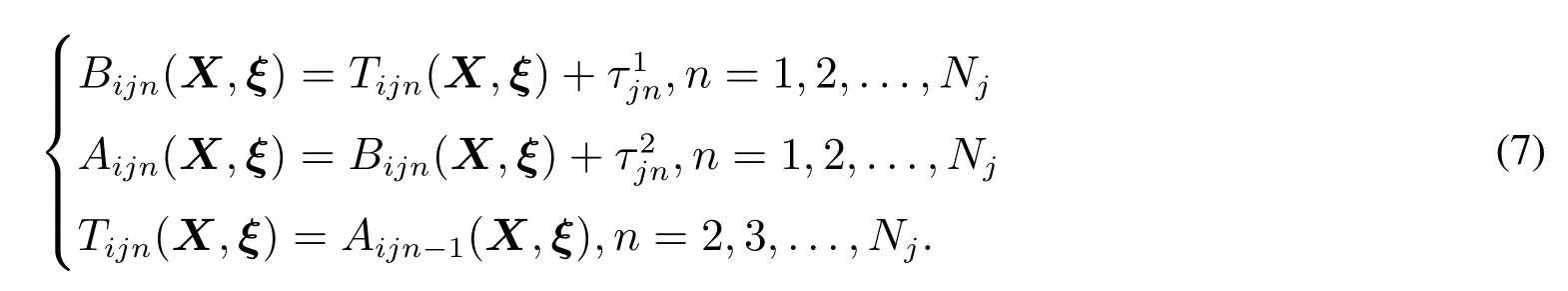
已知列车i在各站间的速度曲线,根据动能定理,可以得到t时刻列车i在第j站站间的第n个区间产生的动能为

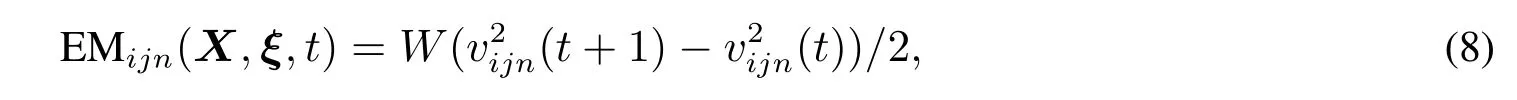
阻力消耗的能量为

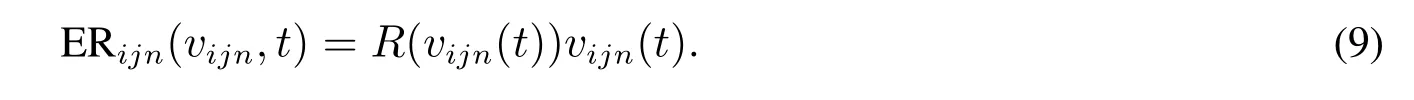
因此,对于每一个时间单元[t,t+1],列车i加速需要的能量可表示为

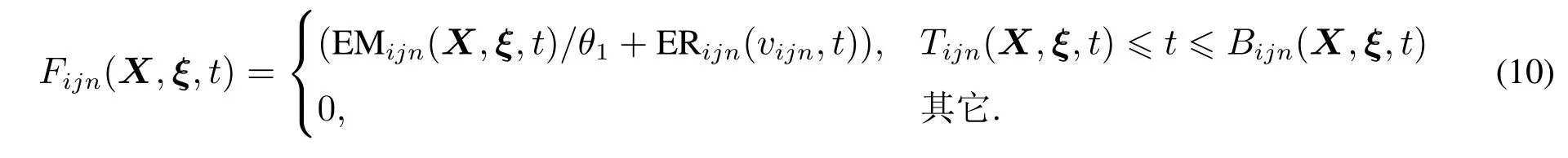
根据式(7)可知,只有当 Tijn(X,ξ,t)≤t≤Bijn(X,ξ,t)时,即列车处于牵引阶段时,才会有加速工况出现,并需要为加速过程提供能量.其他时间均处于制动阶段,加速需要的能量为0.

牵引阶段不仅包括加速工况,还有巡航和惰行工况,其中巡航和惰行工况动能为非正值.为了只求得列车加速时需要的能量,只需得到Fijn(X,ξ,t)中非负的值即可.因此,将式(7)修正为

同样的,对于每一个时间单元[t,t+1],列车i制动可以回收的能量可表示为

在式(12)中,只有当列车处于 Bijn(X,ξ,t)≤t≤Aijn(X,ξ,t)时,即制动阶段时,才会产生回收能量,其他时间列车没有再生能量回收.

若考虑共有I辆列车,每辆列车在同一区间具有相同的速度曲线且在同一车站具有相同的停站时间,则整条线路上全部列车的再生能量利用量可表示为

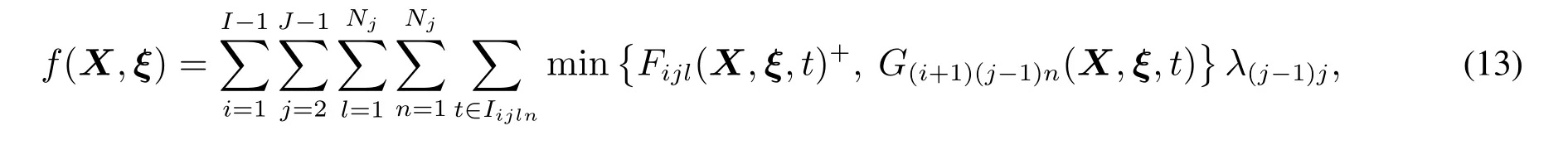
其中

2.7 随机机会约束规划模型

本文以最大化再生能量利用量为目标函数,即f(X,ξ).通过最大化目标函数f(X,ξ)的α−乐观值,达到提高再生能量利用率的目的.本文建立的随机机会约束规划模型如下.

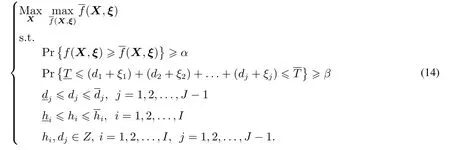
模型(14)以最大化再生能量利用量的α−乐观值为目标.其中α和β是事先给定的置信水平,是再生能量利用量函数的α−乐观值

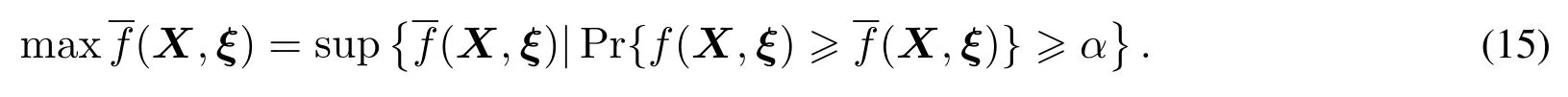
第二个约束保证总的旅行时间以β的置信水平满足时间窗约束;第三个和第四个约束确保停站时间和每辆车的发车间隔符合时间窗的约束,以更好地满足乘客的需求;第五个约束是为了保证最优解为整数.

本文所研究的时刻表优化方法的创新点在于:1)发车间隔是非均匀的,通过调整列车的发车间隔,使得再生能量的利用率提高;2)建立基于数据驱动的模型,以真实数据取代传统动力学方程描述的速度曲线,使得模型的建立更加准确和可靠;3)从乐观值的角度出发,以最大化再生能量利用量乐观值为目标,建立随机机会约束规划模型.

3 猴群算法

本文建立的基于数据驱动的地铁节能时刻表随机机会约束规划模型具有决策变量多,目标函数和约束条件复杂的特点,因此使用传统优化方法进行求解将花费大量计算时间.为了求解所建随机机会约束规划模型,需要使用一种优化过程设计科学有效,不会陷入局部最优,能够适应所建模型结构且计算时间合理的智能算法.猴群算法(Monkey Algorithm,MA)是由Zhao等[28]于2008年提出的一种在求解多维,大规模,多峰优化问题时体现出明显优势的新型群智能优化算法.猴群算法通过模拟自然界中猴群爬山的过程,设计了初始化,爬过程,望过程,跳过程和终止条件等步骤.其中初始化利用随机方法产生每个猴子的初始位置,爬过程利用目标函数的伪梯度来逐步改善优化模型的目标函数值,望过程是在猴群达到局部最优后寻找相邻区域内更优解的过程,而跳过程则迫使猴群由当前区域转移到新的区域,以避免算法局部最优.猴群算法优越的全局优化性能已被广泛应用于求解各种复杂优化问题,如:输电线扩展规划问题[29],入侵检测问题[30],传感器优化问题等[31,32].本文在猴群算法望过程之后设计信息共享机制来避免猴群中信息不对称造成的局部最优解优劣差异,从而更好的找寻全局最优解.猴群算法的流程图如图4所示.

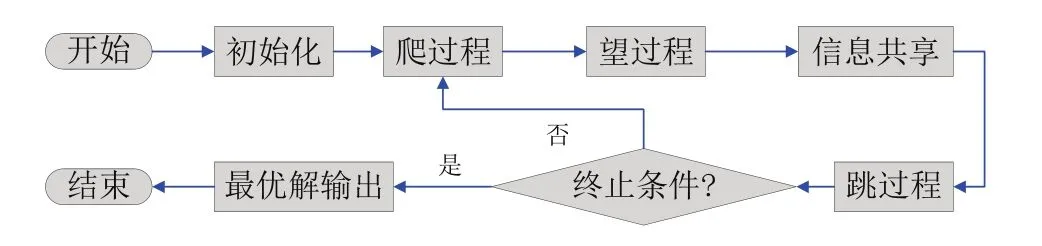
图4 猴群算法流程图Fig.4 The flow chart of Monkey Algorithm

3.1 解的表示及初始化

设猴群规模为正整数M,第m只猴子的当前位置用向量Xm=(xm1,xm2,...,xmn)表示,m=1,2,...,M.每只猴子的位置实际上对应所建立随机机会约束规划模型的一个决策向量,也即代表模型的一个可行解.Xm由两部分决策变量组成:列车的发车间隔时间和列车在车站j的停站时间,也即Xm=(h1,h2,...,hI;d1,d2,...,dJ−1)且n=I+J−1.

从可行域中随机产生M个可行解(猴子)作为猴群算法的初始种群,初始化过程的算法设计如下:

步骤1对第m 只猴子,随机产生解向量其中且i=1,2,...,I,产生随机列车发车间隔;且j=1,2,...,J−1,产生随机列车停留时间.

步骤2若Xtemp满足模型的约束条件,则令Xm=Xtemp为第m只猴子(可行解);若不满足,则重复步骤1直至得到第m只猴子,也即第m个可行解;

步骤3重复步骤1至步骤2,直至产生M只猴子.

3.2 爬过程

猴群算法的爬过程是一个通过迭代不断改变猴子所处位置以改善模型目标函数值的过程.在本文中,爬过程可通过连续迭代来优化所建随机机会约束规划模型的可行解,使其不断逼近最大再生能量利用量的取值.为避免过多地使用目标函数的梯度信息,与采用梯度法的牛顿法不同,猴群算法采用伪梯度法[33,34]的思想,仅计算当前相邻位置的目标函数值,以逐步移动的方式设计算法的爬过程.设第m只猴子的当前位置为Xm=(xm1,xm2,...,xmn),m=1,2,...,M.爬过程设计如下:

步骤 1对第 m 只猴子,随机产生向量 ΔXm=(Δxm1,Δxm2,...,Δxmn)T,其中 Δxmk是从区间[−φ,φ]中随机产生的整数,φ为爬过程的步长,m=1,2,...,M,k=1,2,...,n;

步骤2若则

步骤3重复步骤1至步骤2,直到达到设定的爬次数Nc.

猴群算法中定义的参数φ称为爬步长,φ越小,求解出的结果越精确,但往往导致较长计算时间.对于规模较大的求解模型,φ值可适当设置得较大或采取变动的爬步长值.

3.3 望过程

在爬过程结束之后,猴群中的每只猴子都到达了各自所处位置附近的最高峰,也即求解的随机机会约束规划模型的目标函数达到了局部最优解,但未必是全局最优.猴群算法的望过程是使每只猴子在局部最优的位置上,在一定视野范围ρ内向周围眺望,观察在其邻近区域内是否有比当前所处的山峰更高的山峰,也即寻找是否存在比目标函数的局部最优解更优的更优解.若猴子发现更高的山峰,就会从当前的山峰跳向更高峰所在的区域,继续通过爬过程找到新区域内的最高峰.对于第m只猴子,m=1,2,...,M,其望过程如下:

步骤1设猴子眺望的视野为ρ;

步骤2设随机产生整数1,2,...,n;

步骤3若满足模型约束条件,则使

步骤4重复步骤2至步骤3,直到达到设定的望次数Nw.

猴群算法望过程中定义的视野范围参数ρ代表猴子所能眺望到的最远距离.ρ越小,求解出的结果越精确,但往往增加运算时间.对于规模较大的求解模型,ρ值可适当设置得较大或采取变动的视野范围.

3.4 信息共享机制

猴群算法在经过爬-望过程后,猴群中的每只猴子各占山头(达到局部最优解),然而每只猴子位置的不同造成局部最优解也存在优劣差别.通过信息共享机制,以便让猴群之间的信息进行交流,从而使处于较高位置的猴子与处于较低位置的猴子进行合作,增强了算法的寻优能力和解的多样性.

设在当次迭代的所有猴子中的最高位置为第m只猴子的当前位置Xm=(xm1,xm2,...,xmn),m=1,2,...,M,设计猴群算法的信息共享机制如下:

步骤1随机产生实数γ∈[0,1];

步骤2记1,2,...,n;

步骤3若满足模型的所有约束条件,则使

步骤4对更新的X1,X2,...,XM重复爬过程.

3.5 跳过程

猴群算法跳过程的主要目的是使猴子从当前的区域转向新的搜索区域,防止算法陷入局部极值导致搜索停滞.以当前猴群的重心所在位置为跳跃支点,每只猴子沿着当前所处位置指向支点的方向跳向新的搜索区域.设猴子跳跃的最大范围为[c,d],跳过程设计如下:

步骤1随机产生实数η∈[c,d];

步骤2计算=1,2,...,n,记g=(g1,g2,...,gn)T为跳跃支点;

步骤3计算xmk+Round(η|gk− xmk|),m=1,2,...,M,k=1,2,...,n;

步骤 4若满足所求解模型的所有约束条件,则使并重复爬过程.

3.6 终止条件

在经过以上爬过程,望过程,信息共享,跳过程步骤后,猴群算法完成第一次迭代,猴群中所有猴子的位置得到更新.重复迭代循环一定次数Imax直到最优解保持不变后,算法终止并输出最优解.

4 数值算例

将北京地铁亦庄线(见图5)的数据应用于模型(13),并给出数值算例证明模型(13)的有效性和意义.

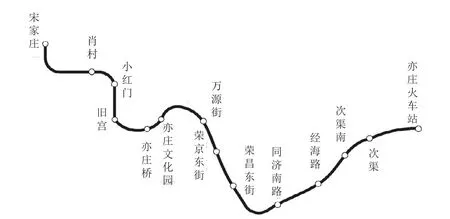
图5 北京地铁亦庄线Fig.5 Beijing Yizhuang subway line

北京地铁亦庄线将北京经济技术开发区与北京主城区紧紧连接在一起,为高端产业的发展提供了坚实的交通保障,也使开发区的企业员工和社区居民有了更为便捷的交通方式.亦庄开发区19万余名企业员工,近4万社区居民可以近距离搭乘地铁直达市区.亦庄线共有14个车站和6个变电站,其中亦庄文化园,荣昌东街和同济南路站客流量较大.因此,针对以上三个车站设置了无延迟,轻微延迟和严重延迟三种情景,并设置了相应的可能性,即p1j=0.7,p2j=0.2和p3j=0.1.亦庄线当前的运行时刻表如表2所示.根据亦庄线的真实速度曲线,表3给出了各站间的牵引和制动时间.

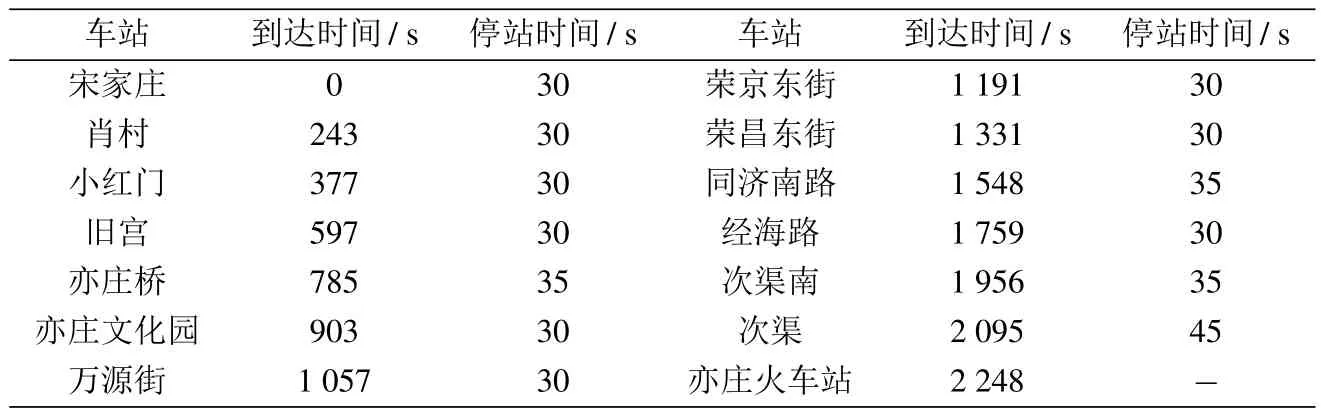
表2 亦庄线当前时刻表Table 2 The current timetable for Beijing Yizhuang subway line

模型中的其他参数设置见表4.

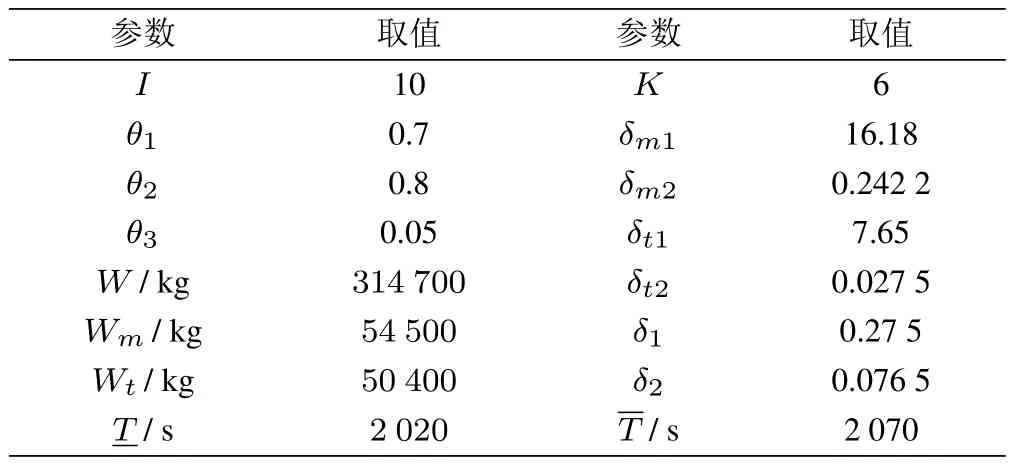
表4 模型中的参数设置Table 4 The parameter setting of model

在运行猴群算法之前,首先对猴群算法进行收敛性实验.通过程序迭代,得到猴群算法的相关参数设置如表5所示,算法性能如图6所示.

表5 猴群算法中的参数Table 5 The parameters setting of MA

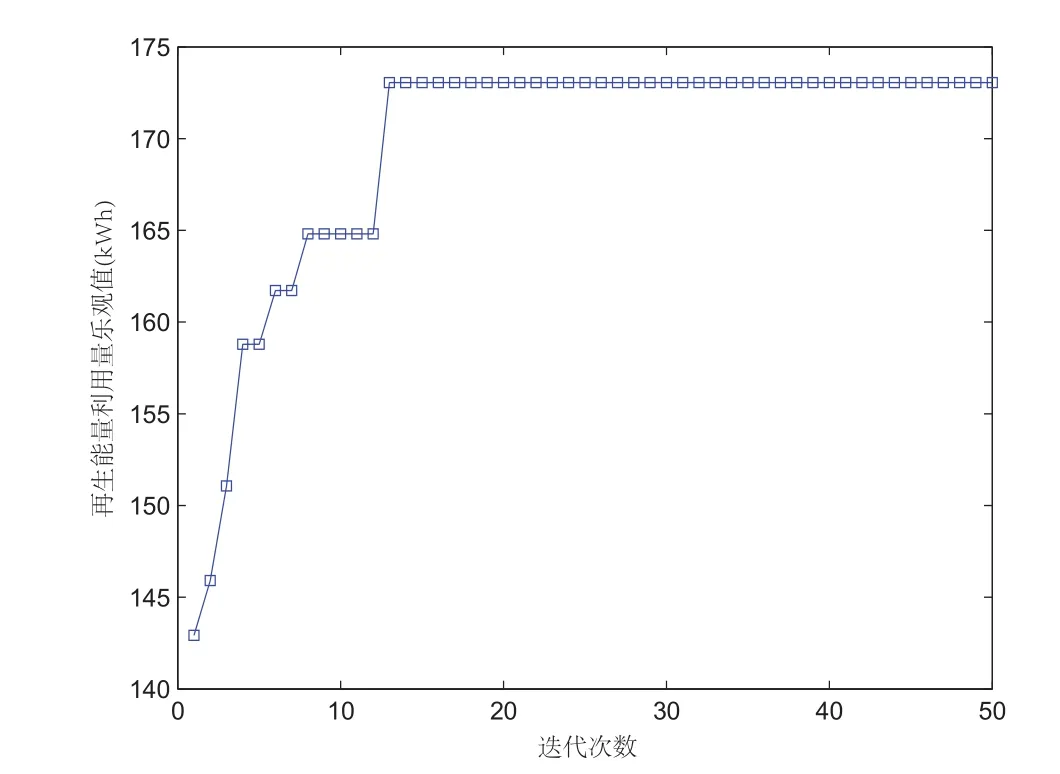
图6 猴群算法算法迭代性能分析Fig.6 The analysis on iterative performance of MA

然后,分别针对置信水平α和β进行实验,研究其对最优解的影响.固定α=90%,求解当β取95%,90%,80%,70%和60%时的最优解.同样的,再固定β=90%,求解当α取95%,90%,80%,70%和60%时的最优解,结果如表6所示.

从表6中可以看出,随着α和β的不断减小,不同延迟情景下再生能量利用量乐观值会不断增大.因此,本文一方面为了提高再生能量利用量的最坏估计,选取α=95%;另一方面,为了使得总运行时间以更高的置信水平符合时间窗的约束,提高时刻表的鲁棒性,选取β=95%.但是在其他领域或模型的应用中,可以根据策略和实际情况的不同选取不同的置信水平.

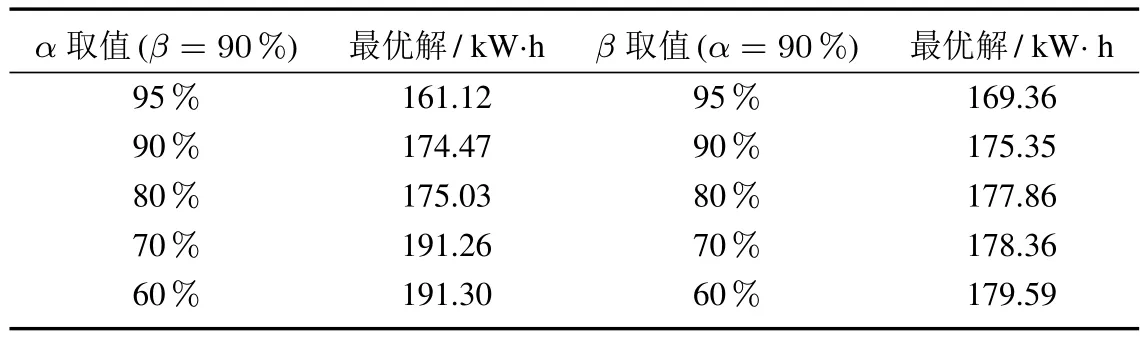
表6 置信水平α和β对最优解的影响研究Table 6 Influence of confidence level on the optimal solution

根据乘客流量和需求等特点,北京地铁亦庄线主要出现早高峰,晚高峰和平峰三种现象.早高峰和晚高峰时期乘客需求较大,列车发车间隔会缩短.同时,发车频率上升也使得这段时间内的能耗较大.因此,如何降低早高峰和晚高峰的能耗也是地铁节能优化的重要环节.本文分别针对早高峰和晚高峰时段,设置发车间隔的变动范围为[330,390]和[290,350],并设计最优时刻表,对此时段内的再生能量利用量进行优化.通过运行猴群算法,计算出早高峰时段的再生能量利用量乐观值为168.33 kW·h.晚高峰时期的再生能量利用量乐观值为171.94 kW·h,其最优时刻表分别如表7和表8所示.

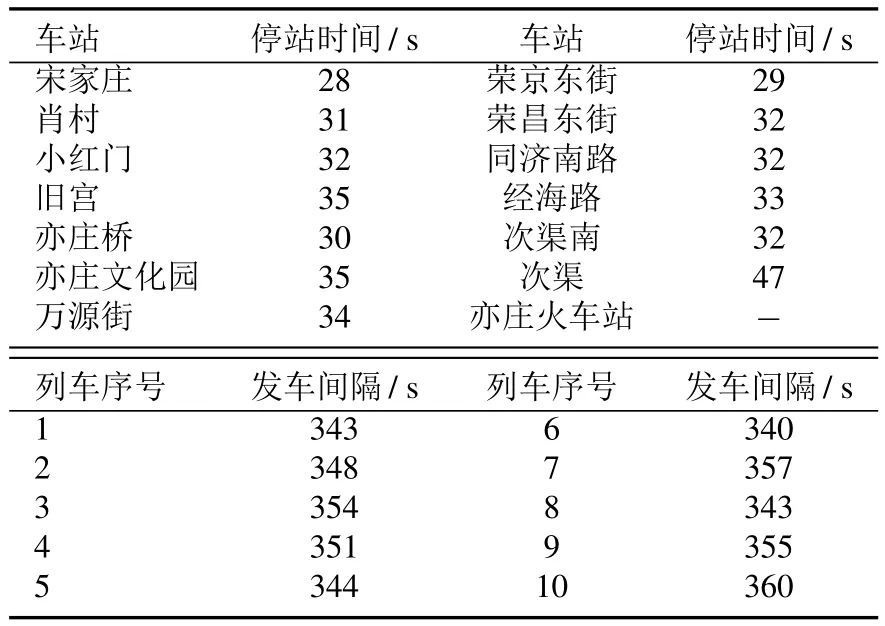
表7 早高峰时段最优时刻表Table 7 The optimal timetable of morning peak hours

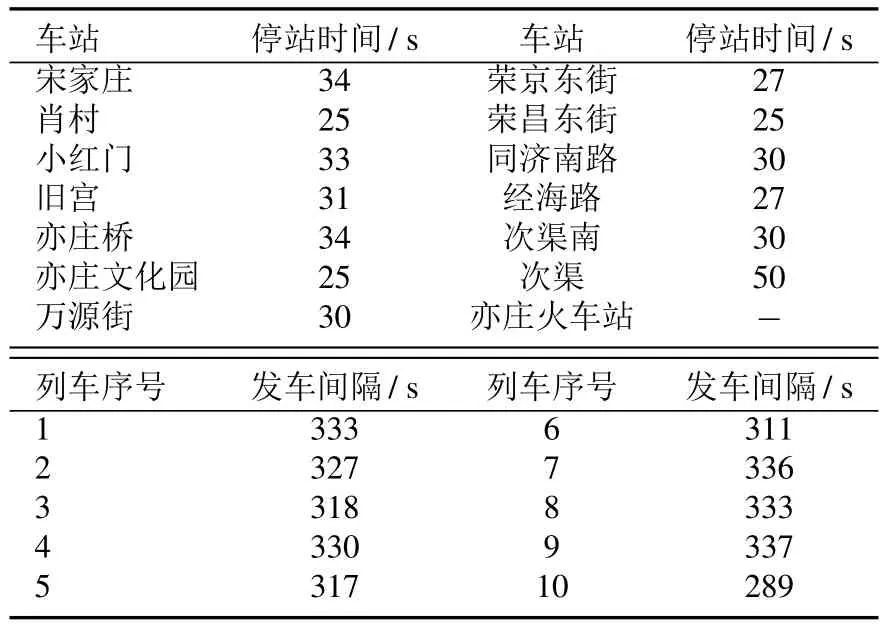
表8 晚高峰时段最优时刻表Table 8 The optimal timetable of evening peak hours

从表中可以看出,相比当前时刻表,为了增大牵引阶段和制动阶段的重叠时间,某些车站会做出调整使得站间运行时间增大,比如:小红门站,旧宫站,亦庄火车站站等;同时也会有一些车站的停站时间会减小,比如:亦庄桥站,荣京东街站,同济南路站等.此外,列车的发车间隔也会做出相应调整,以早高峰时段为例,第3,4,7等辆列车的发车间隔增大,第1,2,5等辆列车的发车间隔减小;以晚高峰时段为例,第1,2,4等辆列车的发车间隔增大,第10辆列车发车间隔减小.

另一方面,当前北京地铁亦庄线的时刻表在早高峰和晚高峰时段的发车间隔分别固定在350 s和300 s.为了分析非均匀发车间隔的时刻表对于提高再生制动能量利用量的意义.令北京地铁亦庄线在各站的停站时间与当前时刻表保持一致,运用猴群算法优化列车非均匀的发车间隔,使得时刻表的再生能量利用量乐观值最大化.通过计算,得到最优时刻表在早高峰和晚高峰时段的再生能量利用量乐观值分别为160.39 kW·h和158.59 kW·h,对应的发车间隔见表9和表10.

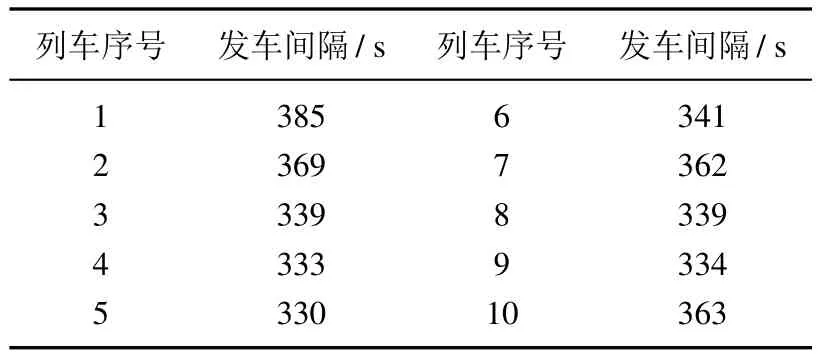
表9 早高峰时段最优发车间隔Table 9 The optimal headway time of morning peak hours

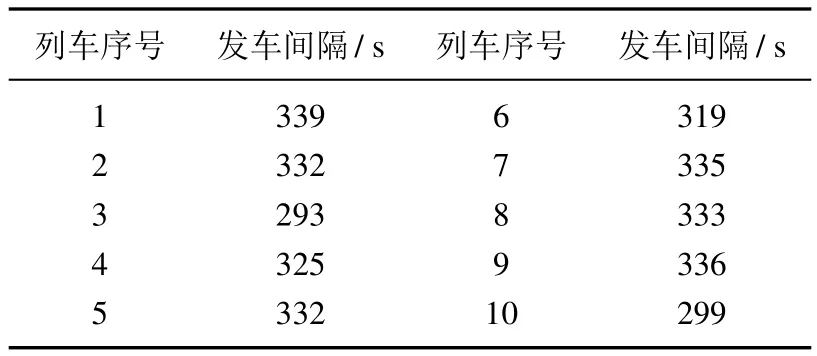
表10 晚高峰时段最优发车间隔Table 10 The optimal headway time of evening peak hours

此外,通过计算,得到均匀发车间隔的北京地铁亦庄线当前时刻表在早高峰和晚高峰时段的再生能量利用量乐观值分别为147.90 kW·h和40.47kW·h.因此,本文的最优时刻表相比于现行时刻表的再生能量利用量可以提高至少8.44%,其对比结果如图7所示.算例分析的结果表明优化非均匀的发车间隔有利于提高地铁系统的再生能量利用率.

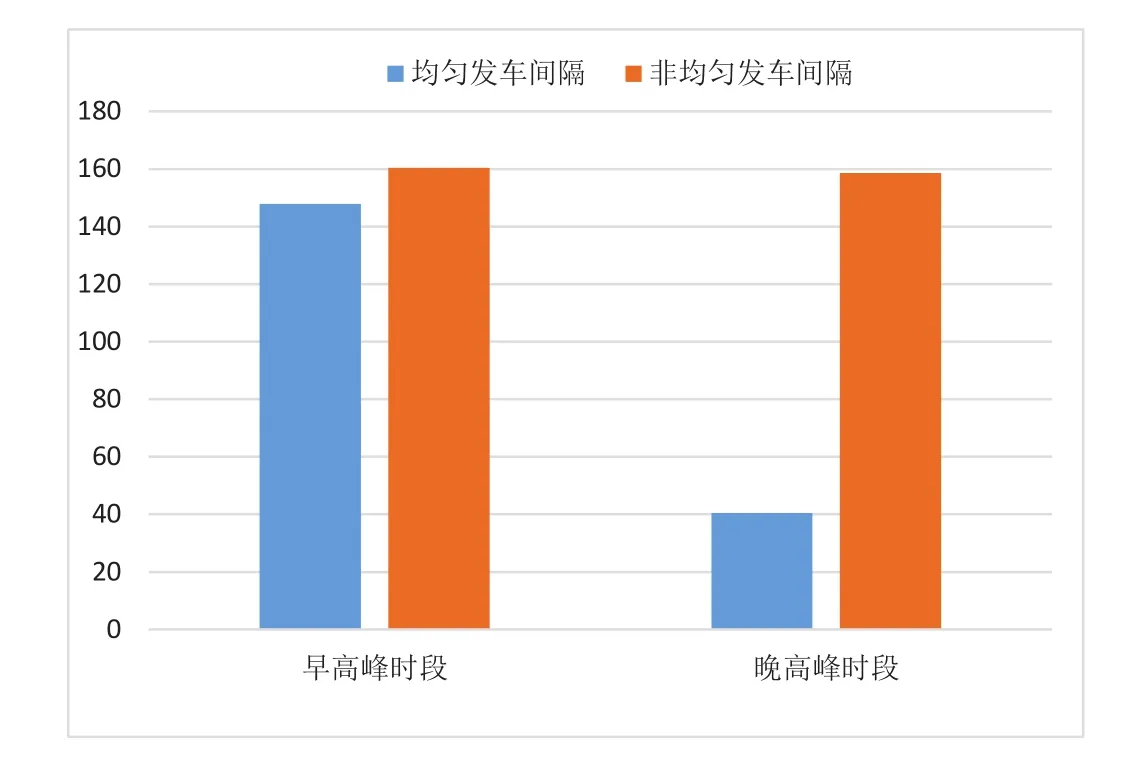
图7 均匀发车间隔与非均匀发车间隔再生能量利用量乐观值对比图Fig.7 Comparison chart of optimistic value between uniform and non-uniform headway time

5 结束语

本文以最大化再生能量利用量为目标,基于地铁真实的运动轨迹,构建数据驱动的时刻表随机机会约束规划模型,为地铁运营管理提供了新的思路和方法.该模型通过调整停站时间和非均匀的发车间隔,提高再生能量的利用率,从而实现地铁节能运行.此外,本文还设计了猴群算法进行求解并基于北京地铁亦庄线的真实数据开展了模拟仿真.结果表明基于本模型的地铁运营早高峰和晚高峰时段的再生能量利用量乐观值分别为168.33 kW·h和171.94 kW·h.与北京地铁亦庄线现行时刻表相比,通过优化非均匀的发车间隔可至少提高再生能量利用量8.44%.

本文将机会约束规划思想与运营调度问题相结合,对列车时刻表进行优化,不仅适用于地铁系统,还可扩展应用于高铁,城际列车的时刻表优化问题中.另外,对于地铁系统而言,在进行节能优化的同时还要考虑乘客需求,时刻表鲁棒性等多种因素.因此,如何协调这些因素之间的关系将成为下一步研究的主要方向.

[1]Ogasa M.Energy saving and environmental measures in railway technologies:Example with hybrid electric railway vehicles.IEEJ Transactions on Electrical and Electronic Engineering,2008,3(1):15–20.

[2]Yang X,Li X,Ning B,et al.A survey on energy-efficient train operation for urban rail transit.IEEE Transactions on Intelligent Transportation Systems,2016,17(1):2–13.

[3]Gordon S P,Lehrer D G.Coordinated train control and energy management control strategies//Proceedings of the 1998 ASME/IEEE Joint.IEEE,1998:165–176.

[4]Chen J F,Lin R L,Liu Y C.Optimization of an MRT train schedule:Reducing maximum traction power by using genetic algorithms.IEEE Transactions on Power Systems,2005,20(3):1366–1372.

[5]Li X,Lo H K.Energy minimization in dynamic train scheduling and control for metro rail operations.Transportation,Part B:Methodological,2014,70:269–284.

[6]周剑斌,苏 浚,何泳斌.地铁列车运行再生能利用的研究.城市轨道交通研究,2004,7(4):33–35.Zhou J B,Su J,He Y B.Utilization of train’s regenerative energy in metro system.Urban Mass Transit,2004,7(4):33–35.(in Chinese)

[7]颜邦杰,张辰秋,林志铭.捷运列车排点与节能.交通信息与安全,2011,29(1):139–144.Yan B J,Zhang C Q,Lin Z M.The MRT train scheduling and energy saving.Journal of Transport Information and Safety,2011,29(1):139–144.(in Chinese)

[8]Ramos A,Pena M T,Fernández A,et al.Mathematical programming approach to underground timetabling problem for maximizing time synchronization//Proceedings of the International Conference on Industrial Engineering and Industrial Management,IEEE,Madrid,Spain,2007:88–95.

[9]Peña-Alcaraz M,Fernández A,Cucala A P,et al.Optimal underground timetable design based on power flow for maximizing the use of regenerative-braking energy//Proceedings of the Institution of Mechanical Engineers,Part F:Journal of Rail and Rapid Transit,2012,226(4):397–408.

[10]Yang X,Chen A,Li X,et al.An energy-efficient scheduling approach to improve the utilization of regenerative energy for metro systems.Transportation Research,Part C:Emerging Technologies,2015,57:13–29.

[11]步 兵,丁 奕,李辰岭,等.列车控制与行车调度一体化节能方法的研究.铁道学报,2013,35(12):64–71.Bu B,Ding Y,Li C L,et al.Research on integration of train control and train scheduling.Journal of the China Railway Society,2013,35(12):64–71.(in Chinese)

[12]Yang X,Li X,Gao Z,et al.A cooperative scheduling model for timetable optimization in subway systems.IEEE Transactions on Intelligent Transportation Systems,2013,14(1):438–447.

[13]Li X,Lo H K.An energy-efficient scheduling and speed control approach for metro rail operations.Transportation Research,Part B:Methodological,2014,64:73–89.

[14]Yang X,Li X,Ning B,et al.An optimisation method for train scheduling with minimum energy consumption and travel time in metro rail systems.Transportmetrica B:Transport Dynamics,2015,3(2):79–98.

[15]Albrecht A,Howlett P,Pudney P,et al.The key principles of optimal train control:Part 1:Formulation of the model,strategies of optimal type,evolutionary lines,location of optimal switching points.Transportation Research,Part B:Methodological,2016,94:482–508.

[16]Albrecht A,Howlett P,Pudney P,et al.The key principles of optimal train control:Part 2:Existence of an optimal strategy,the local energy minimization principle,uniqueness,computational techniques.Transportation Research,Part B:Methodological,2016,94:509–538.

[17]Xu X, Li K, Li X. A multi-objective subway timetable optimization approach with minimum passenger time and energy consumption.Journal of Advanced Transportation.Journal of Advanced Transportation,2016,50(1):69–95.

[18]Li X,Yang X.A stochastic timetable optimization model in subway systems.International Journal of Uncertainty,Fuzziness and Knowledge-Based Systems,2013,21(S):1–15.

[19]Charnes A,Cooper W W.Chance-constrained programming.Management Science,1959,6(1):73–79.

[20]Liu B.Uncertain Programming.Hoboken,New Jersey:John Wiley&Sons,Inc.,1999.

[21]刘宝碇,赵瑞清,王 刚.不确定规划及应用.北京:清华大学出版社,2006.Liu B D,Zhao R Q,Wang G.Uncertain Programming and Application.Beijing:Tsinghua University Press,2006.(in Chinese)

[22]周爱莲,李旭宏,毛海军.一类企业物流中心动态选址模型研究.系统工程学报,2011,26(3):360–366.Zhou A L,Li X H,Mao H J.Research on a multiple-period dynamic location model of enterprise logistics centers.Journal of Systems Engineering,2011,26(3):360–366.(in Chinese)

[23]肖 宁.求解随机机会约束规划的混合智能算法.计算机工程与应用,2010,46(22):43–46.Xiao N.Stochastic chance-constrained programming problems with hybrid intelligent algorithm.Computer Engineering and Applications,2010,46(22):43–46.(in Chinese)

[24]石 莉,杨善林,马 英,等.一种新的组合权重集结方法及合理性评价研究.系统工程学报,2012,27(4):481–491.Shi L,Yang S L,Ma Y,et al.A novel method of combination weighting for multiple attribute decision making.Journal of Systems Engineering,2012,27(4):481–491.(in Chinese)

[25]王洪峰,王 娜,汪定伟,等.一种求解多峰优化问题的改进Species粒子群算法.系统工程学报,2012,27(6):854–864.Wang H F,Wang N,Wang D W,et al.Improved species-based particle swarm optimizer for multi-modal optimization problems.Journal of Systems Engineering,2012,27(6):854–864.(in Chinese)

[26]赵瑞清,郝士鹏.一类新的模糊约束满足问题的建模与求解.系统工程学报,2010,25(3):415–420.Zhao R Q,Hao S P.Modeling and solving a novel class of fuzzy constraint satisfaction problems.Journal of Systems Engineering,2010,25(3):415–420.(in Chinese)

[27]Xiao X.The Record of Vehicle Condition for Beijing Metro Yizhuang line.Technical Report.Beijing Mass Transit Railway Operation Corporation Limited,2014.

[28]Zhao R,Tang W.Monkey algorithm for global numerical optimization.Journal of Uncertain Systems,2008,2(3):165–176.

[29]王靖然,余贻鑫,曾 沅.离散猴群算法及其在输电网扩展规划中的应用.天津大学学报,2010,43(9):798–803.Wang J R,Yu Y X,Zeng Y.Discrete monkey algorithm and its application in transmission network expansion planning.Journal of Tianjin University,2010,43(9):798–803.(in Chinese)

[30]张佳佳,张亚平,孙济洲.基于猴群算法的入侵检测技术.计算机工程,2011,37(14):131–133.Zhang J J,Zhang Y P,Sun J Z.Intrusion detection technology based on monkey algorithm.Computer Engineering,2011,37(14):131–133.(in Chinese)

[31]Yi T H,Li H N,Zhang X D.A modified monkey algorithm for optimal sensor placement in structural health monitoring.Smart Materials and Structures,2012,21(10):105033.

[32]伊廷华,张旭东,李宏男.基于改进猴群算法的传感器优化布置方法研究.计算力学学报,2013,30(2):218–223.Yi T H,Zhang X D,Li H N.Optimal sensor placement based on monkey algorithm.Chinese Journal of Computational Mechanics,2013,30(2):218–223.(in Chinese)

[33]Kiefer J,Wolfowitz J.Stochastic estimation of the maximum of a regression function.The Annals of Mathematical Statistics,1952,23(3):462–466.

[34]Spall J C.An overview of the simultaneous perturbation method for efficient optimization.Johns Hopkins APL Technical Digest,1998,19(4):482–492.