基于逻辑回归模型的泥石流易发性评价与检验：以金沙江上游奔子栏—昌波河段为例

吴赛儿，陈 剑，ZHOU Wendy，高玉欣，徐能雄

(1.中国地质大学(北京) 工程技术学院，北京 100083; 2.Colorado School of Mines, Department of Geology and Geological Engineering, Colorado Denver 80401)

0 引 言

泥石流作为我国最频发的地质灾害之一，多发生于半干旱山区以及高原冰川区，其分布遍及我国31个省、市和自治区，全国有1 583个县(市)长期受到泥石流灾害的困扰，每年要暴发数千起泥石流灾害，其活动区域面积达480万km2，共计8万多处，其中活动强烈的泥石流有8 500多处，面积达130万km2[1-2]，多爆发于西南、西北的广大山区，在空间和时间上有分布广泛但相对集中的特征。近年来，频发的泥石流灾害直接造成了平均每年近千的人员伤亡和>10亿元的经济损失[3]。因此，以探究区域泥石流特点、分析在特定环境下的致灾因子、进行泥石流预测与评价等为主的研究工作备受关注。作为风险评价的基础，通过泥石流的易发性评价来直观反映泥石流灾害的空间分布，不仅可以完善当前灾害程度的评估，同时也为预防潜在灾害的战略准备提供参考，对于预测预警、防灾减灾工作意义重大。目前，国内外不少学者开展了广泛的研究，在泥石流的形成条件、堆积特征、影响因素、评价方法方面取得了重要成果[4-20]。

本文应用多元统计分析方法中的逻辑回归(LR)模型，以GIS为操作平台，基于小流域为评价单元开展干热河谷泥石流易发性评价与检验。LR模型的自变量既可以是连续变量，也可以是二分类或多分类变量，易于用来预测具有二项特点的概率问题，并且与区域遥感影像资料的结合有很好的适应性和应用价值。随着LR模型和GIS技术应用于地质灾害空间预测的理念被国外学者Gorsevski提出后[21]，LR模型的可操作性在地质灾害空间预测方面已得到很好的证实，尤其在滑坡灾害敏感性评价中得到较广泛的应用[21-27]。近年来该方法在泥石流评价方面的应用逐渐引起重视[28-30]。

本文研究区为金沙江上游奔子栏—昌波河段一带，覆盖面积3 105 km2，地形上属于高山峡谷地区，切割强烈[31]。作为我国“西部大开发”战略的重要地区之一，该区域内泥石流等地质灾害的频发对周边的水利水电工程和公路工程建设构成严重威胁。目前，在研究区泥石流堆积扇成因机制和泥石流易发性评价方面已经取得一些显著成果[32-36]，但就泥石流预测评价而言，在评价指标的选取、标准化处理、评价结果精度及检验方法等方面尚有待改进。为弥补前期评价工作的不足，探讨如何有效地对评价结果进一步验证，本文采用逻辑回归模型对金沙江上游奔子栏—昌波河段的泥石流易发性进行了评价和检验。

1 区域地质概况及泥石流分布

1.1 研究区地质概况

研究区分布于四川、云南、西藏交接处的金沙江上游徐龙—奔子栏一带(图1)，地处我国西南横断山区；在地貌单元上，位于以“世界屋脊”著称的青藏高原南东缘，横断山脉中段；地理坐标为98°55′—99°25′E，28°00′—29°20′N。

图1 研究区位置与地貌图Fig.1 Location and geomorphic map of the study area

地理位置对年降水量分布的影响主要体现在谷地对外来水汽的遮蔽。研究区峡谷深切、高山对峙，河谷相对高差达1～1.5 km[31]，受西南季风和东南暖湿气流影响水汽难以进入，研究区处于“雨影区”，表现为典型干热河谷型气候。在金沙江河谷的奔子栏到四川得荣一带，年降水量只有300 mm左右，巴塘至得荣间金沙江河谷年降水量少于400 mm[36]。降水季节分布极不均匀，6月至9月雨量非常集中，一般占80%以上，雨季旱季分化明显。同时，研究区气温在时间和空间上，呈现极大的垂直分布温差变化。每年6月份河谷最高气温可达30 ℃以上，每年1月至2月高山区最低气温则降至-30 ℃。该区特殊的自然条件造成植被不发育、地表风化剥蚀强烈[31]。

研究区位于濒临欧亚板块与印度板块相互碰撞带的东缘，沉积构造环境复杂多样，火山活动极其强烈、频繁，分布多条构造岩浆岩带、变质带、紧密褶皱冲断层带，但地震活动性相对较弱，震级均小于6级。区内岩性复杂。纵贯南北的金沙江断裂将该区分为东、西两个地层区，东区出露地层为石炭系、上二叠统和下二叠统、中—下三叠统，岩性主要为灰岩、板岩、砂岩、片岩。二叠系地层在西区分布较广，中—下三叠统、二叠系下统下部地层主要分布在西区东北部以及金沙江沿岸，主要出露岩性为板岩、砂岩、火山岩、灰岩[23,25]。研究区内滑坡、边坡失稳、崩塌等不良地质现象发育，地质构造带破碎，岩石风化剥蚀强烈，全区物理风化现象较为强烈(图2)，为泥石流提供了充足的松散破碎固体物源。

1.2 泥石流分布

通过遥感解译和现场调查资料分析，在研究区范围内，直接进入金沙江干流河谷和主要支流的泥石流共有91条(图2)，共涉及流域面积约1 274 km2，占研究区总面积的44.5%。其中沟谷型泥石流66条，广泛发育于全区，涉及流域面积约1 242 km2，平均流域面积18.8 km2；坡面泥石流25条，分布于金沙江沿岸的斜坡地带，涉及流域面积32 km2，平均流域面积为1.28 km2[35]。

图2 研究区泥石流流域分布图Fig.2 Distribution map of debris flow catchment in the study area

2 数据准备与研究方法

2.1 基础数据与评价单元

本文使用的数据主要包括30 m×30 m分辨率的DEM、Landsat 8遥感影像、1∶5万区域地形图和地质图、降水资料等。研究区被30 m×30 m的方格分为3 472 074个栅格单元，其中泥石流栅格单元1 545 073个。由于泥石流发生区域的平面形状多呈狭长展布，以往普遍以栅格或规则网格为单元的泥石流评价方法即便在GIS软件中易于划分与计算，但其存在割裂流域整体性的弊端，因此，本文以不规则小流域作为单元开展评价，以提高易发性评价区划和检验的精度。

2.2 方法与步骤

研究工作分为5步进行：

(1)通过GIS平台，基于研究区30 m×30 m分辨率的数字高程模型(DEM)，综合考虑野外调查、航空影像、交通图中河流分布现状，采用GIS水文分析模块将研究区划分为220个小流域，根据现场踏勘和遥感影像解译的泥石流分布点，进而分为91个泥石流样本和129个非泥石流样本；

(2)选择可能促使历史泥石流发生的评价指标并借助软件(ArcGIS10.0和ENVI 5.0)，通过DEM数据、数字地质图、降水资料、Landsat 8遥感影像得到指标图层并栅格化；

(3)对各项指标标准化处理后的流域样本通过SPSS软件进行75%的随机抽样，创建训练组和检验组数据，前者用来构建LR模型，后者用来检验模型效果；

(4)尝试指标全部组合并利用ROC曲线测试模型效果，拟合最佳的LR模型被采用；

(5)利用模型得到易发性评价分区图，最后通过检验测试评价结果的精度与可靠性。

2.3 评价指标选取

为保证选取指标的有效性，基于LR模型的泥石流易发性评价在两个假设前提下进行：(1)预测的潜在泥石流将发生在与历史泥石流相同或近似环境中；(2)在分析中使用的指标在未来相当长的时间内不会发生明显改变。

根据专家打分法和前人泥石流评价资料，初步选取了泥石流危险性评价中常用的评价指标，并进行了相关性分析以确认被选指标对泥石流发生起到了控制作用。初步选择坡度(F1)、坡向(F2)、流域相对高差(F3)、沟壑密度(F4)、岩性(F5)、植被归一化指数(F6)、距断裂带距离(F7)、距主干道路距离(F8)、地表粗糙度(F9)、雨季月平均降雨量(F10)，共10项作为评价指标。

2.4 指标的分类与标准化处理

将选取的10项评价指标作为一级指标然后再进行分类，得到的二级指标使用了不同的量纲，有必要进行标准化处理后得到统一尺度的标准指标值，再作为回归变量导入模型以发挥作用。指标标准化消除了连续变量(坡度、流域相对高差等)和离散变量(岩性)的数据类型差异，简化了在建立模型时对于离散变量进行哑变量设置这一步骤，同时，也为后续指标的评价分析提供直观的数据。

LR模型指标量化方法多归于两种，第一种按照公式(1)计算标准化指标值Xi,j：

(1)

其中：i=1，2，3，…，n，为一级指标编号；j=1，2，3，…，m，为二级指标序号；si,j是各二级指标下已发泥石流面积，km2。在某些研究中，si,j被替换为ni,j，表示各二级指标下已发泥石流沟谷数。

第二种指标量化方法[30]中，引入各二级指标分类后面积Si,j以及初始指标值Mi,j，计算方法如下：

(2)

(3)

第一种方法仅仅反映了各二级分类指标对灾害的影响程度；第二种方法不仅考虑了各二级指标下灾害的分布情况，也体现了二级指标本身的分布情况，本文采用第二种方法进行指标标准化。

2.5 逻辑回归模型

二元逻辑回归模型是一种反映二值分类响应变量(因变量)对一个或多个回归变量 (自变量) 进行分析的对数模型，其结果反映某种事件的发生概率。在泥石流易发性评价中，二值响应变量代表泥石流事件发生与否，即1代表泥石流发生，0代表不发生[30]；回归变量为各评价指标数据，可以是连续变量，抑或是分类变量，以此构建评价模型。

假设泥石流灾害发生概率记作P，值域分布[0，1]，取P/(1-P)的自然对数，即对P作Logit转换。记评价指标集[x1，x2，…，xn]为自变量，建立LR方程：

lgP=Z=C+B1x1+B2x2+…+Bnxn

(4)

(5)

其中：C为常数，表示无灾害隐患条件下响应变量事件发生概率与不发生概率之比的对数值；B1，B2，…，Bn为逻辑回归系数，表示某个指标改变一个单位量时，响应变量事件发生概率与不发生概率之比的对数值，通过对训练样本的求解得到其值。

已知逻辑回归系数，利用指标值x1，x2，…，xn，便可计算各流域单元灾害发生概率P，进而根据P值划分灾害易发性等级。

3 奔子栏—昌波河段泥石流易发性评价分区与检验

3.1 评价指标分析

将初步选取的10项一级评价指标通过等间隔划分，得到各一级指标下的二级指标分区。随后依据公式(2)和公式(3)进行标准化处理，并对计算获得的各标准化指标值重赋值。赋值越大表示二级指标对泥石流灾害事件发生的贡献越大，赋值范围[1，j]。指标标准化及重赋值结果如表1所示。由表1可见各二级指标对研究区地形地貌的控制程度(Mi,j)、各二级指标对研究区泥石流发育的影响程度(Xi,j)，以及标准化指标与泥石流发育的相关性等级(重赋值)。由此对单一指标进行致灾影响性分析。

(1)坡度：地面坡度在地表径流、地下水补给与排泄、松散物源堆积等方面起到重要的控制作用，从而间接影响泥石流的发育。研究区坡度分布区间为[0°，67°]，泥石流发育的优势坡度为20°～30°。当坡度<20°不利于泥石流的启动；坡度>40°时，不利于碎屑物源的积累。

(2)坡向：坡向控制着山坡小气候和水热比的分布规律。阳坡和阴坡相比，阳坡受到日照强度和辐射较多，冰雪消融快，岩石风化速度快、程度高，岩土结构较为松散，因此泥石流物源较为丰富。造成阳坡泥石流一般比阴坡发育的现象。由表1可见，研究区内各坡向均有发育，但阳坡泥石流发育略具优势。

(3)流域相对高差：高差变化控制着地表植被发育和基岩裸露情况，研究区位于金沙江上游，山势陡峻，河流下切强烈，高山峡谷地形十分发育，为泥石流启动提供动力条件。其中，相对高差在600～900 m范围内泥石流发育比较集中。

(4)沟壑密度：该指标表征研究区的水系发育与分布。沟壑在地表水的下蚀、搬运和沉积的交替作用下形成，同时也受地质构造、地层岩性、气候等因素的影响，受到内外地质营力的共同作用。研究区内，随沟壑密度增大，泥石流发育的优势成“U”形分布，即沟壑密度较大或较小时均有利于泥石流发生。

(5)岩性：根据风化严重程度和岩性破碎程度将研究区地层岩性分类。区内出露的板岩、片岩、砂岩、灰岩风化严重，形成的坡积物为泥石流提供主要的物源。由表1可见，处于强烈风化等级地区的泥石流最为发育。本区第四系松散堆积物零星分布，所占比例较少，不足以成为泥石流物质的主要来源。

(6)植被归一化指数(NDVI)：植被增强了岩土体抗剪强度和土壤固结程度，防止水土流失，是影响并判断泥石流分布的重要因素之一。全区NDVI值域为[0，0.7]，在该值处于0.1～0.3之间时，地表多为基岩出露与裸土地带，有利于泥石流发育。

(7)距断裂带距离：研究区构造形迹以南北向为主，其次为北西向与北北西向构造，褶皱、断裂构造发育。断裂构造的交叉复合部位岩土体尤其破碎，产生的松散碎屑物质为泥石流发育提供了物源储备。距离断裂构造500～1 000 m处为研究区泥石流发育的优势区间。

(8)距主要道路距离：这一项指标在一定程度上反映了人类活动作用。研究区主要道路靠近金沙江干流，海拔较低，属于干热河谷气候。主要道路地带植被不发育，岩土物理风化严重，加上人类活动如修路切坡、伐木毁林等现象在这一带集中，导致近公路段成为泥石流敏感区。

表1 指标分级与重赋值

(续)表1 指标分级与重赋值

(9)地表粗糙度：反映地表微地形，即地表起伏变化与侵蚀程度。地表粗糙度对近地面风速等风沙活动造成影响，同时也反映了地表的抗风蚀能力。该指标被定义为地表单元曲面面积与投影面积之比。从表1分析结果来看，该指标与泥石流发育的相关性不显著，需要在后续建立模型过程中进一步观察，再决定该指标的保留与否。

(10)雨季月平均降雨量：降雨是泥石流主要触发条件之一。研究区为干热河谷，年均降雨量<400 mm，时空分布不均，雨季旱季分化明显。每年6月至9月为雨季，降雨强度达到峰值，雨量集中。表1的分析结果显示，随降雨量增加，泥石流发育程度越高。

3.2 评价模型建立与ROC检验

对研究区的220个小流域样本进行75%随机抽样，将得到的流域样本数据组成训练组来建立LR模型；余下25%的流域样本组成检验组，用来检验评价效果的可靠性。

训练组样本数据如果不能覆盖各二级分类指标区间，意味着抽样不全面，建模效果将会受到影响，因此有必要对抽样建组结果进行复核。如图3所示，经随机抽样得到的全体样本数据、训练组样本数据、检验组样本数据在各个二级指标中的分布趋势基本吻合，且各区间不存在抽样空白，证明抽样结果均衡有效。

将训练组样本数据的各评价指标的标准化指标值Xi,j作为模型的回归变量，泥石流事件Yi作为响应变量，基于SPSS10.0软件进行回归分析。

在LR模型建立过程中，当选取的评价指标全部参与建模时可能导致评价结果不显著。为了明确对研究区泥石流事件的发生贡献突出的指标，找到预测模型的最优指标组合，在选择参与拟合的指标时，本文采用了评价指标体系的全部组合方式来进行建模，再利用受试者工作特征曲线(ROC曲线)一一检测模型拟合效果。

如表2所示，加*的AUC值所对应的指标在变量数相同的模型组中，表现了最优的建模拟合效果，因此，该指标在模型组中被保留下来进而引入下一个变量。以此类推，当模型中引入变量9时，AUC已达到最高值0.827，说明继续加入第10个变量对模型的拟合效果并没有良性影响。因此，选择AUC为0.827时的模型作为最终评价模型，保留参与该建模过程中的9项指标，并剔除坡向指标F9。最优模型的ROC检验结果如图4所示。研究区泥石流易发性评价模型表达式如下：

Z=-10.396+4.957F1-2.278F2+4.860F3+
4.619F4+8.274F5+2.374F6+
7.687F7+16.349F8+6.975F10

(6)

表3和表4分别显示了LR模型拟合统计量值和逻辑回归系数及相关统计参数，在逻辑回归系数B的分析结果中，除坡向F2、沟壑密度F4两项指标Sig值分别为0.065、0.055，略大于0.05，其他7项指标Sig值均小于0.05，本模型基本通过了5%显著性水平检验，可用于进一步评价。

表2 55组LR模型AUC值测试结果

注：在建模过程中引入相同数量的变量时，测试效果最佳的模型AUC值以“*”的形式来表示。

表3 LR模型拟合统计量

注：df为自由度；Sig为显著性；-2LL为似然函数的自然对数的-2倍；Cox & SnellR2和NagelkerkeR2为伪决定系数。

表4 逻辑回归系数及相关统计参数

注：B为模型中各个参数的回归系数；S.E.(Std.Error)为标准误差；Wals为Wald检验得到的统计量；df为自由度；Sig为显著性。

3.3 评价结果分析与总体检验

通过ArcGIS10.0将建立的LR模型运用到指标分级重赋值处理后的图层组进行合成，得到研究区泥石流易发性概率图。认为易发性概率P大于0.5时，泥石流易发性等级为高或极高；概率小于0.1时，认为易发性等级为极低。基于此，将研究区划分为5个等级区，即极低易发区(P=[0，0.1])，低易发区(P=[0.1，0.3])，中等易发区(P=[0.3，0.5])，高易发区(P=[0.5，0.7])，极高易发区(P=[0.7，1])。研究区泥石流易发性等级区划图、评价结果分区统计如图5和表5所示。

评价结果显示，研究区泥石流集中发育在昌波—贡波、徐龙—古学的金沙江干流沿岸一带，局部高发区分布在瓦卡流域处。中等易发区与极低易发区的分布范围分别占全区的29.78%、12.79%，同比其他3区分别处于较大和较小两个极端，但差异并不悬殊，总体上看来，5个等级分区面积比较均衡。在极高易发区，实际发育泥石流面积465.46 km2，共计32个泥石流流域，泥石流灾害占该分区面积的75.95%，占研究区灾害总面积的37.15%；高易发区的泥石流面积349.46 km2，共发育泥石流流域26处，占分区面积的69.24%，占全区灾害总面积的27.89%；中等易发区发育泥石流面积334.07 km2，包含24个泥石流流域，占分区面积的36.12%，占全区灾害总面积的26.66%；低易发区和极低易发区共计存在泥石流流域9处，泥石流流域面积合占全区灾害总面积的8.30%。在极高易发区和高易发区中，已发泥石流流域共计58处(全区泥石流流域共91处)，占全区泥石流流域数量的63.7%，占全区灾害面积的65.0%；在极高易发区、高易发区以及中等易发区中，已发泥石流流域共计82处，占全区泥石流流域数量的90.1%，占全区灾害面积的91.7%。由此可见，高易发区与低易发区的分区界限清晰且灾害易发性区别显著，泥石流主要发育在中等以及中等以上易发性分区内。

图3 全体样本、训练组样本、检验组样本在各指标中的分布频率统计图Fig.3 Histograms for the training and testing data subsets

从极高易发区至极低易发区，分区泥石流面积与分区总面积比值、分区灾害面积与全区灾害总面积比值的分布呈现不同幅度的下降趋势，说明各分区之间的灾害易发性具有明显的等级变化特征。从总体检验来看，泥石流易发性评价和分区结果与实际情况吻合较好。

3.4 样本个案检验

在SPSS 25%随机抽样操作下的检验组样本数据共计55个，包含24个泥石流流域和31个非泥石流流域。利用检验组样本对本次易发性评价结果进行验证与检测，结果如表6和表7所示。表6显示了训练组样本总体预测精度检验结果，P为预测发生灾害概率，当P>0.5即判断为泥石流流域，得到的预测命中率为70.8%；判断非泥石流流域时，在P值分别<0.3和<0.5的水平下，非泥石流流域判断命中率分别为64.5%、81.6%，两种情况下，样本预测整体命中率为67.7%和76.2%。

图4 泥石流易发性评价模型ROC曲线检验Fig.4 ROC curve of the LR-based debris-flow susceptibility assessment model

图5 研究区泥石流易发性等级分区图Fig.5 Debris-flow susceptibility map of the study area

表7显示了检验组55个样本流域在各区的分布，对比该样本中实际泥石流流域分布情况可见，本次LR模型在各分区的抽样调查中也有较好的表现。随着易发性等级降低，检验组样本中实发泥石流流域数量显著减低。个体预测准确性方面，极高易发区个体样本预测一致率为91.7%；其次为高易发区，达到75.0%。二者较高的预测正确率也说明，泥石流集中发生于极高易发区与高易发区。评价结果经个案检验证明预测效果良好。

表5泥石流易发性评价结果统计

Table5Statisticsofdebris-flowsusceptibilityassessmentresults

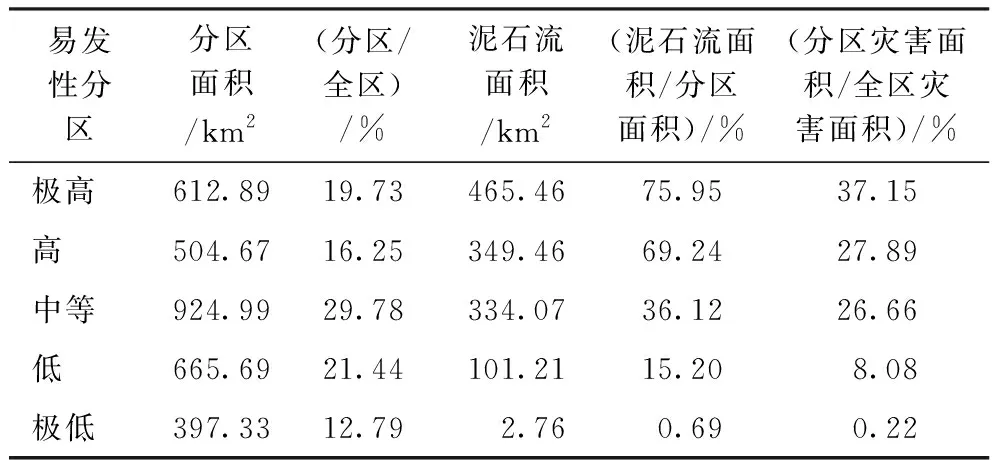
易发性分区分区面积/km2(分区/全区)/%泥石流面积/km2(泥石流面积/分区面积)/%(分区灾害面积/全区灾害面积)/%极高612.8919.73465.4675.9537.15高504.6716.25349.4669.2427.89中等924.9929.78334.0736.1226.66低665.6921.44101.2115.208.08极低397.3312.792.760.690.22

表6检验组样本总体预测精度检验结果

Table6Resultsoftheoverallforecastingaccuracyforthetestingdatasets

流域预测情况/个实际情况/个命中率/%整体命中率/%泥石流流域P>0.5(极高、高易发区)172038—非泥石流流域P<0.3(极低、低易发区)24313167.7非泥石流流域P<0.570.864.581.676.2

表7 检验组样本分区分布情况与精度

4 讨论与结论

本文对金沙江上游干热河谷区的奔子栏—昌波河段进行了泥石流的易发性研究，并对LR评价模型的建模过程进行优化，强化了评价指标的筛选过程，在评价结果的检验方法方面做出改进，提高了研究区泥石流易发性区划的准确性与评价结果的可靠度，取得主要认识如下：

(1)在指标分析筛选和LR建模方面，初步选取10项，在指标敏感性分析中标定了敏感度较低的指标F9。在建立LR模型时关注了指标筛选与组合，使建立的模型最大化地适用于本区干热河谷，测得模型预测成功率为0.827(AUC)；同时，在建模过程中再次验证了引入指标F9对模型意义不大，因此将指标“地表粗糙度”一项剔除。通过55组模型的预测效果对比发现，同一指标在独立参与评价、与其他指标组合参与评价的两种情况下，发挥作用的权重不尽相同，从而体现了指标评价体系中各致灾因素在泥石流发育过程中的协同与牵制作用关系。

(2)研究区泥石流易发性评价结果表明了本区致灾主导因素的指标排序为：距主干公路距离>岩性>距断裂带距离>雨季月平均降雨量，坡度、坡向、流域相对高差、沟壑密度、植被归一化指数5项指标发挥辅助作用。研究区的主干道路比邻金沙江干流，切坡、修路、砍树伐林等人类活动比较强烈，导致干流两岸的崩塌滑坡以及倾倒变形体较发育，形成了泥石流重要物质来源。由此可判断，在季节性暴雨提供动力条件的影响下，强烈的人类活动因素促进了本区干热河谷泥石流的发育。

(3)对评价结果的可靠性先后进行了易发性区划的总体检验与流域样本的随机个案检验。总体检验表明，以流域数量和流域面积为单位统计，极高易发区和高易发区两处的实发泥石流与全区泥石流比例之和，分别为63.7%和65.0%；在极高易发区、高易发区以及中等易发区三区中，比例分别为90.1%和91.7%，证明了各分区之间的泥石流易发性具有明确的等级变化特点，且泥石流易发区与低发区区别显著，易发性分区结果具有实际意义。随机个案检验结果表明，检验组小流域样本中，被判为泥石流易发流域的样本与实发泥石流流域分布一致的比率随分区易发性等级降低依次为91.7%、75.0%、36.4%、16.7%、0，从流域个案角度证明了各分区泥石流易发性呈现逐级减弱的特征。总体检验与个案检验均证明了泥石流易发性评价结果可靠性良好。

参考文献：

[1] 唐川, 朱静. 云南滑坡、泥石流研究[M]. 北京:商务印书馆, 2003: 76-115.

[2] 谢洪, 钟敦伦, 韦方强, 等. 我国山区城镇泥石流灾害及其成因[J].山地学报, 2006,24(1):79-87.

[3] 罗元华. 论泥石流灾害风险评估方法[J]. 中国矿业, 2000, 9 (6): 70-72.

[4] 李阔, 唐川. 泥石流危险性评价研究进展[J]. 灾害学报, 2007, 22(1): 106-110.

[5] 丛威青, 潘懋, 李铁峰, 等. 基于GIS的滑坡、泥石流灾害危险性区划关键问题研究[J]. 地学前缘, 2006,13(2):185-190.

[6] 罗元华, 陈崇希. 泥石流堆积过程数值模拟及防灾效益评估方法[J]. 现代地质, 2000,14(4): 484-488.

[7] 钟敦伦, 韦方强, 谢洪. 长江上游泥石流危险度区划的原则与指标[J]. 山地研究, 1994, 12(2):78-83.

[8] 刘希林, 陈宜娟. 泥石流风险区划方法及其应用:以四川西部地区为例[J]. 地理科学, 2010,30(4): 558-565.

[9] 崔鹏, 邹强. 山洪泥石流风险评估与风险管理理论与方法[J]. 地理科学进展, 2016, 35(2):137-147.

[10] 王维早, 雷霆, 许强. 基于层次分析法的河北省太行山区泥石流灾害危险性评估研究[J]. 地球与环境, 2010, 38(3): 357-362.

[11] 宁娜, 马金珠, 张鹏, 等. 基于GIS和信息量法的甘肃南部白龙江流域泥石流灾害危险性评价[J]. 资源科学, 2013,35(4):892-899.

[12] 陈晓清, 谢洪. 基于GIS的泥石流危险度区划研究—以拟建向家坝、溪洛镀水电工程库区为例[J]．土壤侵蚀与水土保持学报, 1999,5(6):46-50.

[13] 柳金峰, 黄江成, 欧国强, 等.甘肃陇南武都区泥石流易发性评价[J]. 中国地质灾害与防治学报, 2010,21(4):8-12.

[14] 李为乐, 唐川, 杨武年, 等. RS和GIS技术在区域泥石流危险性区划中的应用研究[J]. 灾害学, 2008,23(2):71-75.

[15] 唐尧, 杨武年. 基于GIS的震后汶川潜在泥石流危险性评价[J]. 上海国土资源, 2012,33(3):57-60.

[16] 吴雨夫,余斌, 亓星, 等. 岷江上游大白杨沟泥石流特征及成因[J]. 现代地质, 2012,26(1):107-113.

[17] 李雅晖. 基于流域尺度的泥石流危险性评价:以岷江流域汶川县为例[D]. 成都: 成都理工大学,2011:21-45.

[18] 戴福初, 李焯芬, 黄志全, 等. 火山岩坡残积土地区暴雨滑坡泥石流的形成机理[J]. 工程地质学报, 1999,7(2):147-154.

[19] SONG S J, ZHANG B L, FENG W L, et al. Using fuzzy relations and GIS method to evaluate debris flow hazard[J]. Wuhan University Journal of Natural Sciences, 2006, 11(4): 875-881.

[20] YUAN L F, ZHANG Y S. Debris flow hazard assessment based on support vector machine[J]. Wuhan University Journal of Na-tural Sciences, 2006, 11(4): 897-900.

[21] GORSEVSKI P V,GESSLER P E,FOLTZ R B. Spatial prediction of landslide hazard using logistic regression and GIS[J].Transactions in GIS, 2000,10 (3):395-415.

[22] 邢秋菊, 赵纯勇, 高克昌. 基于GIS的滑坡危险性逻辑回归评价研究[J]. 地理与地理信息科学, 2004,20(3):49-51.

[23] 刘艺梁, 殷坤龙, 刘斌. 逻辑回归和人工神经网络模型在滑坡灾害空间预测中的应用[J]. 水文地质工程地质，2010, 37(5):92-96.

[24] 许冲, 徐锡伟. 逻辑回归模型在玉树地震滑坡危险性评价中的应用与检验[J]. 工程地质学报, 2012, 20(3): 326-333.

[25] 李雪平, 唐辉明. 基于GIS的分组数据Logistic模型在斜坡稳定性评价中的应用[J]. 吉林大学学报, 2005,35(3):361-365.

[26] OHLMACHER G C, DAVIS J C. Using multiple logistic regression and GIS technology to predict landslide hazard in northeast Kansas, USA[J]. Engineering Geology,2003,69:331-343.

[27] 王志旺, 廖勇龙, 李端有. 基于逻辑回归法的滑坡危险度区划研究[J]. 地下空间与工程学报,2006,2(2): 1451-1454.

[28] 潘赟, 丛威青, 潘懋. 基于GIS的辽宁省岫岩县泥石流灾害危险性区划研究[J]. 北京大学学报,2010,46(4): 601-606.

[29] NETRA R R, JOHN R G, ERIC V M, et al. A comparison of logistic regression-based models of susceptibility to landslides in western Colorado, USA[J]. Landslides,2014, 11:247-262.

[30] 邹强,王青,刘延国. 基于GIS与Logistic模型的公路泥石流易发性分析[J]. 水土保持通报, 2014,34(3):185-189.

[31] 戴福初. 金沙江-奔子栏水电站库区地质构造、环境地质遥感研究研究报告[R].北京：中国科学院地质与地球物理研究所，2005.

[32] 陈剑, 崔之久, 戴福初, 等. 金沙江奔子栏-达日河段大型泥石流堆积扇的成因机制[J]. 山地学报, 2011, 29(3) : 312-319.

[33] 姚鑫, 戴福初, 陈剑. 金沙江干热河谷区地质灾害遥感研究[J]. 长江流域资源与环境,2007,16(5)：655-660.

[34] CHEN J, DAI F C, YAO X. Holocene debris-flow deposits and their implications on climate in the upper Jinsha River valley,China[J]. Geomorphology, 2008, 93: 493-500.

[35] 黎艳,陈剑,许冲. 基于AHP的半干旱区泥石流易发性评价：以金沙江上游奔子栏—昌波河段为例[J]. 现代地质, 2015, 29(4):975-982.

[36] CHEN Jian, LI Yan, ZHOU Wendy, et al. Debris-flow susceptibility assessment model and its application in semiarid mountainous areas of the southeastern semiarid mountainous areas of the southeastern Tibetan Plateau[J]. Natural Hazards Review, 2016.doi:10.1061/ (ASCE) NH. 1527-6996.0000229.