液流旋启式止回阀阀内流场数值模拟

莫才友 向科峰 李 翔

(1.西南科技大学应用技术学院 四川绵阳 621010； 2.西南科技大学制造科学与工程学院 四川绵阳 621010)

液流旋启式止回阀又称单向阀，其作用主要是防止管路中的流体倒流，引起上游泵机组的反转，造成泵机组的烧毁或管路破坏。由于其具有结构简单、体积小、质量轻、安装方便等特点，已广泛应用于化工、石油、核电、自来水等压力管道输送中[1]。目前对其研究主要是关闭时引起的水击问题和结构优化等方面。李树勋等[2]通过二维模型对液流旋启式止回阀在关闭过程中的动态特性进行了数值模拟；韩文伟等[3]对旋启式止回阀在关闭时的水锤进行了研究；曾红等[4]对旋启式止回阀的进行了流场分析与结构优化；张健平等[5]对梭式止回阀与旋启式止回阀流动特性的数值模拟已进行比较分析，由于旋启式止回阀不属于轴对称结构，采用二维几何模型分析结果数据不准确，且采用三维几何模型对其开启、关闭及稳定工作时的振动噪声研究比较少。流体与自身结构对阀门引起振动、噪声、水击等问题起到密不可分的作用[6-7]。本文从旋启式止回阀自身入手，对止回阀的整个工作过程进行模拟，进而通过阀内流场的速度场、压力场、阀瓣运动特性进行数值仿真，分析振动噪声产生的机制。文中根据旋启式止回阀的运动特点，建立阀瓣运动模型与三维几何模型，采用计算流体力学软件ADINA8.9的CFD模块对液流旋启式止回阀开启、稳定、关闭整个过程中阀瓣的运动特性和阀内流场进行数值模拟并实现可视化，为液流旋启式止回阀的结构参数设计和优化提供参考。

1 旋启式止回阀工作原理及结构特点

旋启式止回阀的结构简单，主要是通过压紧螺母将阀瓣与摇杆固定，使摇杆绕一支点自由旋转。其工作原理主要是利用流体对阀瓣产生的冲击力使阀瓣打开，阀瓣处于悬浮状态，流道畅通；当上游流体对阀瓣的作用力小于阀瓣自重时，阀瓣依靠自身重力关闭通口，防止流体倒流[8]。其结构原理图如图1所示。

2 模型建立及参数设置

2.1 几何模型建立及网格划分

考虑到旋启式止回阀自身结构的特殊性与ADINA软件建模的复杂性，利用CATIA软件进行参数化3D建模，并通过IGES数据接口将模型导入ADINA8.9中，然后进行网格划分。其流体与阀瓣模型网格划分如图2和图3所示。

图1 旋启式止回阀结构原理图Fig. 1 Schematic diagram of swing check valve structure

图2 流场网格模型Fig. 2 Grid model of flow field

图3 阀瓣网格模型Fig. 3 Mesh model of disc

2.2 数学模型

2.2.1 基本控制方程

旋启式止回阀由阀瓣和流体所组成的流固耦合系统，应遵循动量与能量守恒原则，因此在流固耦合交界面处，应满足流体与阀瓣应力τ、位移d、热流量q、温度T等变量的守恒或相等[9]。

(1)

在阀门内部的流固耦合系统中，定义在阀瓣和内部流体结构点上的解向量记为Xs和Xf，耦合解向量为X=(Xf,Xs)，另ds=ds(Xs),τf=τf(Xf)，因此阀瓣与流体相互作用下的耦合有限元方程可以表示为：

(2)

其中，Ff和Fs分别是与流体和结构相应的有限元方程，Ff[Xf,0]=0，Fs[Xs,0]=0

2.2.2 阀瓣运动模型

液流旋启式止回阀工作时，阀瓣主要受流体液动力、浮力、自身重力以及阀瓣与阀座之间的支撑力和摩擦力的共同作用。根据牛顿第二定律，主要分析阀瓣在关闭时的运动特性，方程可表示为[10-12]：

(3)

2.3 参数设置

假设0～0.1 s内入口压力从0.1 MPa线性递增至0.14 MPa，0.1～0.6 s为0.14 MPa，0.6～0.7 s线性递减至0.1 MPa，出口背压为0.1 MPa，阀瓣自重10 N，最大旋起角度为80°；采用标准湍流κ-ε模型，阀体内壁为WALL，阀瓣边界为FSI；流体介质为水，且为不可压缩常参数模型，密度为1.0×103kg/m3，黏度为0.001 003 Pa·s，体积模量为1×1020，阀体材料为钢，阀瓣材料为各向同性线弹性材料，弹性模量2.07×1011Pa，泊松比为0.3，密度为7 800 kg/m3，迭代步数为500步。进口压力随时间变化曲线如图4所示。

3 数值模拟结果及分析

取旋启式止回阀在YZ平面上的剖切面MESHPLOT0001，分析在开启阶段、稳定阶段以及关闭阶段不同时刻的速度矢量图与压力云图，并作出阀瓣在3个阶段的速度变化曲线，得出其运动规律。

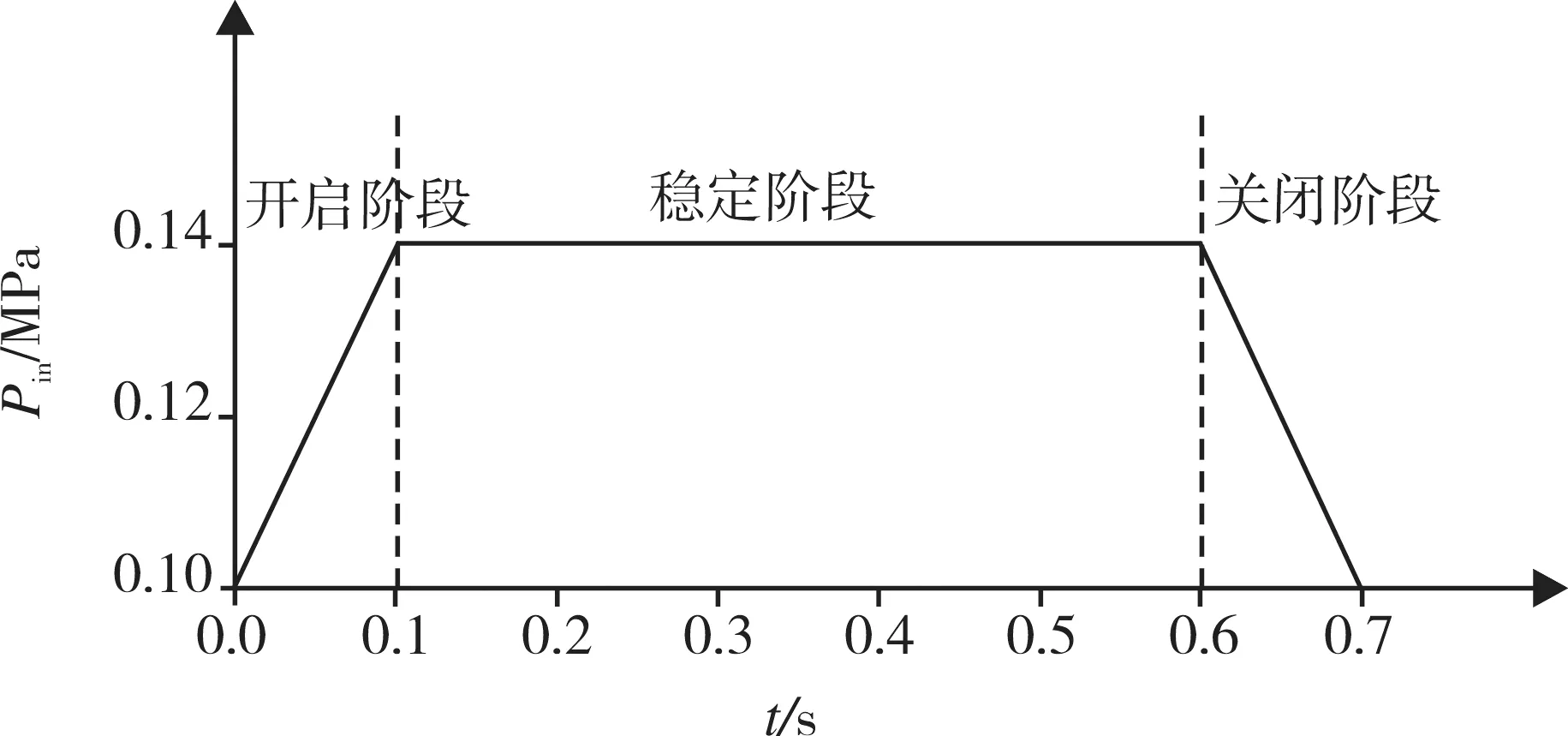
图4 进口压力随时间变化曲线Fig. 4 Variation curve of inlet pressure over time

3.1 开启阶段

阀瓣完全开启时间为0.22 s，取开启阶段t=0.05 s 与0.1 s两个时刻的速度矢量图与压力云图如图5所示，流体速度较大区域位于阀瓣四周缝隙处，最大流速随着进口压力的线性递增不断增加，并以射流的形式向出口喷出，阀瓣背部由于阀瓣四周受液体包裹，瞬时间无流体填充，形成局部真空，但随着阀瓣的不断旋起开度逐渐增大，压缩真空区域逐渐减小，直至流体完全填充真空区域，气穴破灭成许多小的气泡随液体流出，产生噪声。又由于从左到右压力梯度不断增加，阀瓣前端压力明显高于背端，又因阀体结构不对称造成流场压力分布不均，易造成振动和噪声。

3.2 稳定阶段

稳定阶段是指阀瓣完全旋起，流体流动情况几乎不会随着时间的推移发生改变。取稳定工作阶段某一时刻的流场分布情况作分析，图6为稳定阶段t=0.4 s 时的速度矢量图与压力云图，当止回阀阀瓣完全开启，由于止回阀结构设计时通流截面积略大于管道截面积，致使流体在阀门内部的运动速度相比管道流速要小，阀门出口处流体最大流速为20.26 m/s，产生的涡动噪声相比开启阶段明显减弱，在稳定工作阶段阀门的振动噪声显著降低，管道通畅性最佳；止回阀内部进口端压力大于出口端压力，由于阀瓣以及阀体内壁呈凹状且受流体冲击导致压力最大分布区域位于止回阀底部靠阀门出口一端，最大值为195 435 Pa。

图5 开启阶段速度矢量图与压力云图Fig. 5 Velocity vector diagram and pressure cloud diagram at the opening stage

图6 稳定阶段速度矢量图与压力云图Fig. 6 Velocity vector diagram and pressure cloud diagram in stable stage

3.3 关闭阶段

当进口端压力逐渐消失，阀瓣因自重逐渐关闭阀口，即关闭阶段。由于关闭阶段流体作用力几乎不存在，在两端均为大气压力的作用下，由于止回阀在此阶段没有受到泵等其它动力元件的作用，阀瓣在自身重力作用下逐渐关闭阀口，整个关闭时间为0.45 s，较开启阶段持续时间更长，取关闭阶段t=0.75 s与t=1.15 s 两个时刻的速度矢量图与压力云图进行分析(如图7所示)。t=0.75 s时流体速度与压力变化较稳定阶段变化不明显，但t=1.15 s时可看出，在阀门出口处与阀门内部顶端形成了两个较大的漩涡，形成气穴，出口处更明显，但随着流体的进一步流失，失去流体的包裹，气穴与大气融合，逐渐消失。此时刻，最大流速位于管壁处，为 5.538 m/s，随着开度不断减小，涡动尺度递增，涡流压差增大。

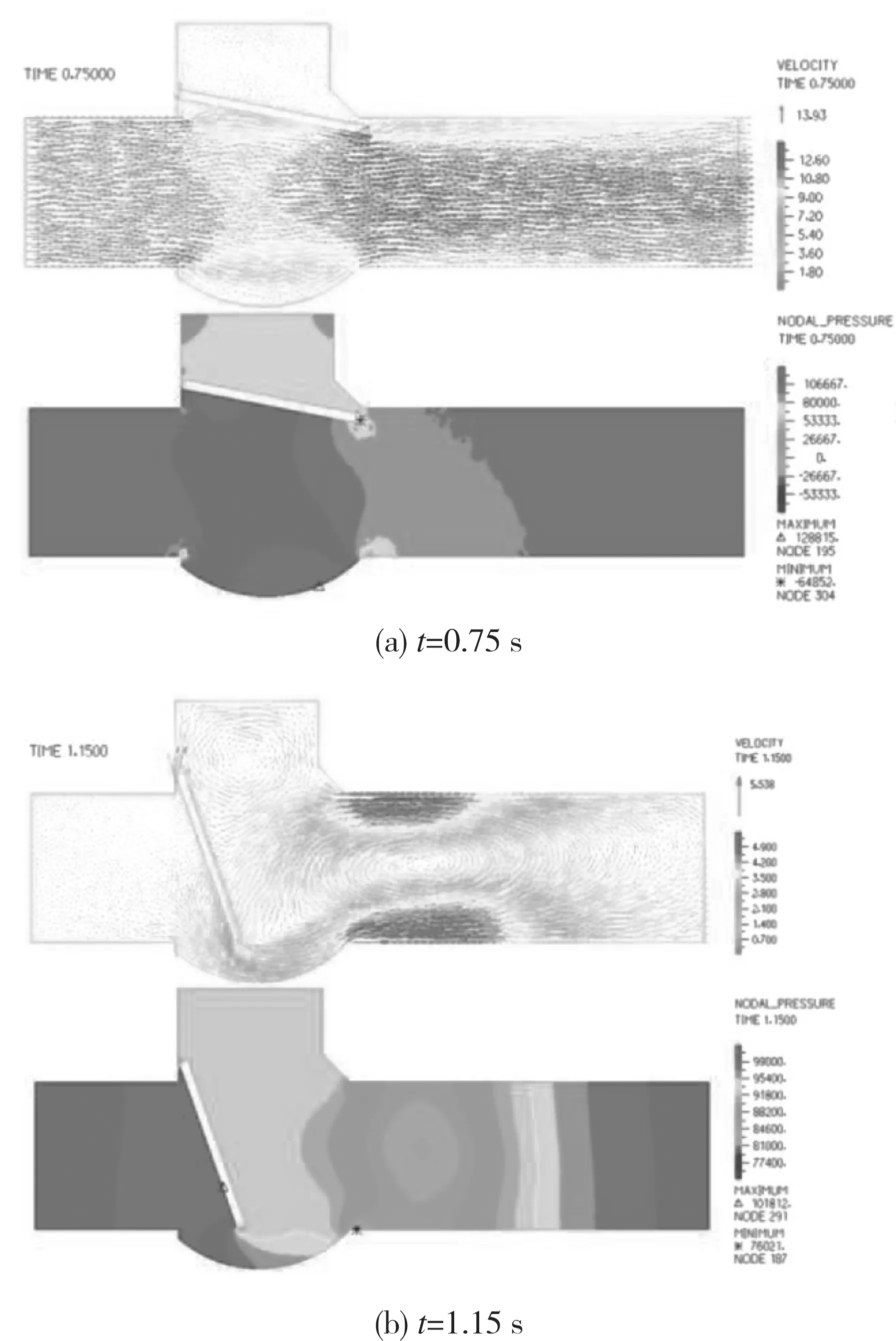
图7 关闭阶段速度矢量图与压力云图Fig. 7 Velocity vector diagram and pressure cloud diagram

3.4 阀瓣运动分析

因阀瓣在分析过程中属于刚体，不会受外力的作用而发生变化，因此取阀瓣末端轴线上的节点54进行分析，得出阀瓣在开启、稳定、关闭阶段的运动规律，图8为阀瓣在3个阶段的速度变化曲线。开启阶段：随着进口压力线性递增，阀瓣运动速度快速增加，但在0.06～0.1 s阶段，由于阀瓣旋起开度陡然增大，流量增大，对阀瓣在轴向上的冲击作用力降低，阀瓣运动速度有一个相对降低的过程，之后又由于进口压力的进一步增大，阀瓣运动速度呈递增趋势；稳定阶段：阀瓣位于最大开度位置，阀瓣静止，速度为零；关闭阶段：由于进口压力线性递减至零，阀瓣在自身重力作用下逐渐关闭阀口，相比开启阶段速度明显偏低，时间延长，阀瓣的关闭造成后端流体回流，撞击阀瓣，产生振动与噪声。

图8 阀瓣运动速度曲线Fig. 8 Velocity curve of disc movement

4 结论

对液流旋启式止回阀内部流场进行数值模拟，并将开启、稳定、关闭完整的动作过程结合在一起进行模拟，体现出整个过程的完整性与数据真实性。可以明显观察阀内流体在整个过程中的流动情况以及压力分布情况，以及阀瓣运动规律，可视化结果为研究液流旋启式止回阀在实际工况下的振动、噪声、涡动以及结构优化提供理论依据与数据参考。

[1] 谢吉兰，韩俊，苏殿顺.旋启式止回阀结构改进[J].阀门，2000, (3):15-19.

[2] 李树勋，侯英哲、李连翠, 等.液流旋启式止回阀关闭动态特性数值模拟[J].排灌机械工程学报, 2013, (4)：335-339.

[3] 韩文伟,韩伟实,郭清,等.旋启式止回阀关阀水锤优化分析[J].原子能科学技术,2014，48(5)：854-860.

[4] 曾红,常学森,魏松. 旋启式止回阀的流场分析及结构优化[J]. 制造业自动化, 2015，37(2)：74-75，79.

[5] 张健平,曾祥炜,陈刚. 梭式止回阀与旋启式止回阀流动特性的数值模拟比较分析[J]. 化工设备与管道, 2014，51(1)：79-82.

[6] 雍歧卫,瞿德刚.止回阀水力特性分析及水击计算[J].阀门，2003,(5):77-81.

[7] 奚伟永.旋启式止回阀故障分析及解决方案[J].阀门，2017,(2):40-43.

[8] 周展浩,宋小鹏.止回阀类型选用的若干技术探讨[J].给水排水，2010,(2):56-61.

[9] 岳戈，梁宇白，陈晨,等.ADINA流体与流固耦合功能的高级应用[M].北京：人民交通出版社，2010:47-61.

[10] 万五一,练继建,李玉柱.阀门系统的过流特性及其对瞬变过程的影响[J].清华大学学报,2005,(12):98-101.

[11] ZHU D L，WU P T，MERKLEY G P，et al．Dripirrigation lateral design procedure based on emission uniformity and field microtopography[J]．Irrigation and Drainage，2010，59(5): 535-546．

[12] WU P T，ZHU D L，JIN J，et al．Design of drip irrigation lateral for optimum capital and operating cost[J]．Water Science and Technology，2010，10(6):943-951．