基于蚁群算法的点焊机器人工作站路径规划

（长春工业大学机电工程学院，吉林长春130012）

0 前言

点焊工艺广泛应用于汽车工业，特别是白车身制造领域中，据统计一台轿车白车身包括4 000～5 000个焊点、55～75个焊接工作站[1]。点焊机器人的路径规划属于典型的TSP（旅行商）问题，如果机器人路径规划不当，会产生点焊机器人运动路径长、工作节拍高、能量消耗大等问题。在点焊机器人路径规划的研究中，通常考虑单工位的路径规划，但点焊机器人工作站一般采用双工位或多工位设计，需要从点焊机器人的一个焊接循环来进行路径规划。

蚁群算法是由意大利学者M.Dorigo等人于20世纪90年代初提出的一种新的模拟进化算法，其真实地模拟了自然界蚂蚁群体的觅食行为[2]。近年来，蚁群算法广泛应用于TSP问题的求解，针对其可能陷入局部最优的缺点，不少专家和学者提出了许多改进方法，文献[3-8]将其他算法（如遗传算法、粒子群算法）与蚁群算法相结合，选择优化蚁群算法的参数，效果良好。但蚁群算法与其他算法相结合并不能解决蚁群算法性能依赖参数设置的问题，采用蚁群算法参数优化法，一般需要逐一分析参数与最优路径之间的关系，工作量较大，求解过程繁琐。为解决上述问题，提出应用正交试验法和回归分析法优化参数。通过运用改进蚁群算法，对汽车后侧围板点焊机器人工作站进行路径规划，最终得到工作站最优或近似的最优路径。

1 工作站路径规划数学模型

汽车后侧围板由后风窗支柱、连接板、后支柱组成，是车身骨架中一个较大的分总成，可靠的支撑着乘员区后部。一辆汽车有2个对称的汽车后侧围板，左右后侧围板各有18个焊点，左后侧围板焊点分布如图1所示。

图1 汽车左后侧围板零件

采用两工位点焊机器人工作站，可以保证点焊机器人的使用效率。点焊机器人工作站布局如图2所示。

图2 汽车后侧围板点焊机器人工作站布局

该问题的数学模型为

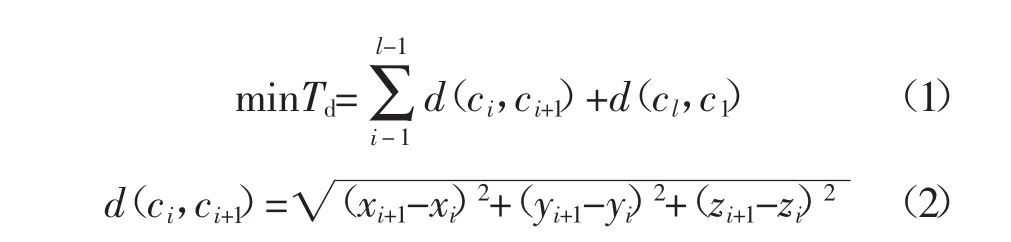
式中 ci∈C；C={c1，c2，c3，…，cl}；i=1，2，3，…，l；ci∈{1，2，3，…，l}；ci≠cj；i，j=1，2，3，…，l。

上述公式中C为焊点集合，ci为焊点的编号，l为汽车后侧围板点焊机器人工作站的焊点个数，d（ci，ci+1）为编号ci和cj两个焊点之间的距离。

2 蚁群算法原理及改进

2.1 蚁群算法原理

蚁群算法中蚂蚁的数量为m，焊点i与焊点j之间的距离为dij（i，j=1，2，3，…，n），t时刻焊点i与焊点j之间连接路径上的信息浓度为τij（t）。初始时，各个焊点之间的信息浓度相同，τij（t）=τ0。

蚂蚁 k（k=1，2，3，…，m），根据各个焊点连接路径上的信息素浓度决定下一个访问焊点，设Pijk（t）表示t时刻蚂蚁k由焊点i转移到焊点j的概率，计算公式为

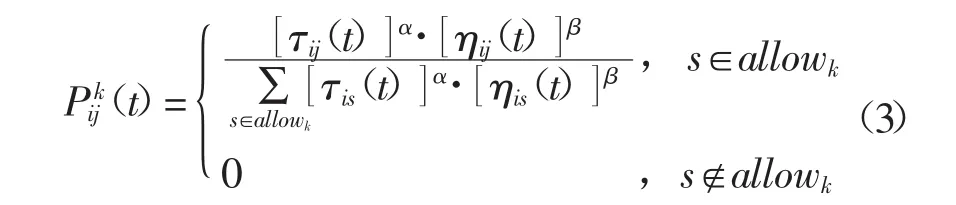
式中ηij（t）为启发函数，取ηij（t）=1/dij，表示从焊点i转移到焊点j的期望程度；allowk（k=1，2，3，…，m）为蚂蚁k待访问城市的集合，开始时allowk有（n-1）个元素，即包括除蚂蚁k出发城市的其他所有城市，随着时间的推进，allowk中的元素不断减少直至为空，即表示所有城市均访问完毕；α为信息素重要程度因子，其值越大，表示信息素浓度在转移中所起的作用越大；β为启发函数重要程度因子，其值越大表示启发函数在转移中的作用越大，即蚂蚁会以较大概率转移到距离较短的城市。

蚂蚁释放信息素的同时，各个焊点之间连接路径上的信息素逐渐消失。当所有蚂蚁完成一次循环后，各个焊点间连接路径上的信息素浓度进行实时更新，即

式中 ρ（0＜ρ＜1）为信息素的挥发程度；Δτijk为第 k只蚂蚁在焊点i与焊点j路径上释放的信息素浓度；τij为所有蚂蚁在焊点i与焊点j路径上释放的信息素浓度之和；Q为常数，表示蚂蚁循环一次所释放的信息总量；Lk为第k只蚂蚁经过路径的长度。

2.2 蚁群算法改进

由蚁群算法原理可知，影响蚂蚁算法求解精度及效率的算法的参数主要有：蚂蚁个数m，信息素重要程度因子α，启发函数重要程度因子β，信息素挥发因子ρ，信息释放总量Q。如果参数选择不当，会导致求解性能下降。

引入正交试验设计方法，找出较优（或最优）的参数设置组合，并根据正交试验结果对参数重要程度进行排序。对最重要的参数，利用回归分析得到参数与最短距离的散点图，根据散点图初步确定该参数与最优解之间的函数关系，用假设检验方法判断该函数关系是否成立。

3 基于蚁群算法的工作站路径规划

运用MATLAB软件编写程序，输入汽车后侧围板点焊机器人工作站各焊点坐标，得到最优路径。

3.1 基于正交试验的蚁群算法参数优化

3.1.1 正交试验方案

蚁群算法的参数取值区间为[9]：m∈因为 n=36，所以 m={1，2，…，20}；α∈[0，5.5]；β∈[1.2，10]；ρ∈[0.3，0.9]；Q={1，2，…，10}，参数水平选取如表1所示。

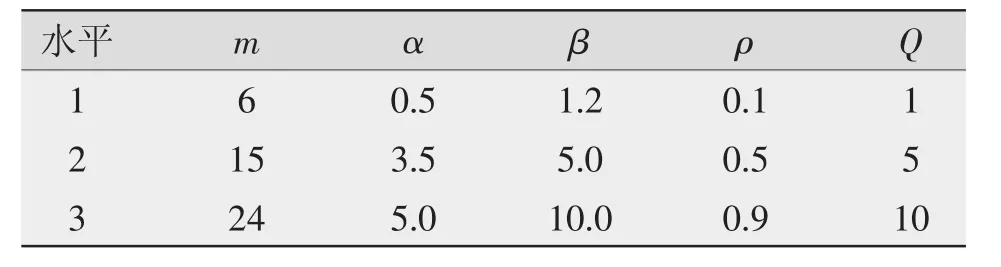
表1 因素水平表

此正交试验是3水平5因素，选L27（313）正交试验表，用MINITAB软件生成正交试验表格，如图3所示，每组试验程序运行20次，记录最优值。

3.1.2 正交试验结果计算与分析

通过MATLAB程序，得到每组试验的最优值为：minTd1=7 071、minTd2=6 975、minTd3=7216、minTd4=6 001、minTd5=6 001、minTd6=6 001、minTd7=6 001、minTd8=6 114、minTd9=6 066、minTd10=6 003、minTd11=5 966、minTd12=6 001、minTd13=6 114、minTd14=6 114、minTd15=6 195、minTd16=6 352、minTd17=6 186、minTd18=6 490、minTd19=6 114、minTd20=6 114、minTd21=6 051、minTd22=6 490、minTd23=6 392、minTd24=6 411、minTd25=6 352、minTd26=6 195、minTd27=6 114。

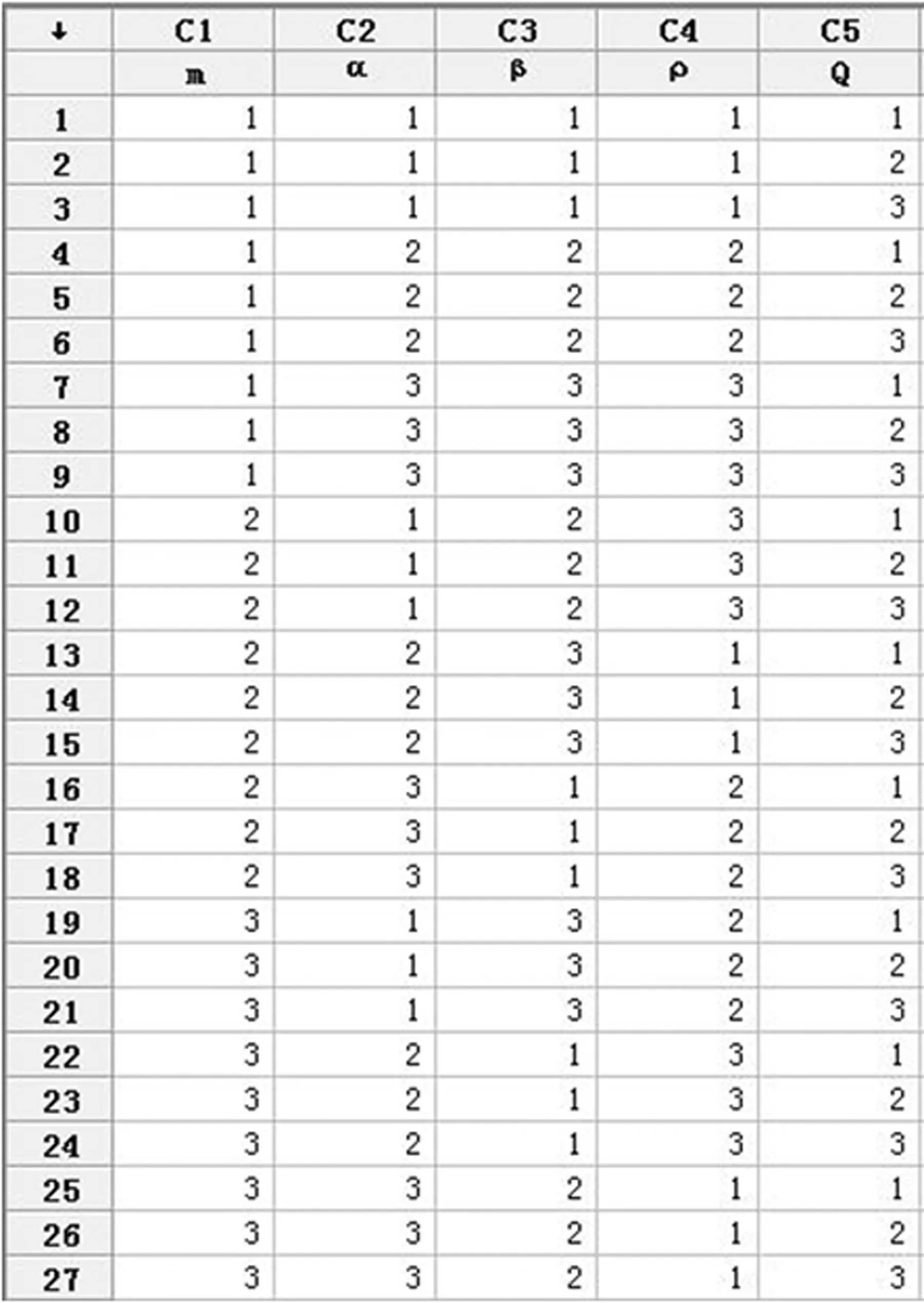
图3 正交试验

利用MINITAB软件分析数据，得到均值主效应图，如图4所示，得到最优组合为m=15，信息素重要程度因子α=3.5，启发函数重要程度因子β=5，信息素挥发因子ρ=0.5，信息释放总量Q=5。

图4 均值主效应

数据分析见图5，影响最优距离的主次因素排序为：β＞ρ＞m＞α＞Q，β为影响最短距离的最主要因素。

3.2 关键参数回归分析

运用回归分析法研究β和最短距离之间的关系，其他参数均用最佳参数设置，得到散点图与β和最短距离之间的函数关系，用假设检验验证函数关系是否成立。回归试验数据见表2，散点图见图6。

由散点图可大致判断，该方程满足二次方程，得到二次回归方程为

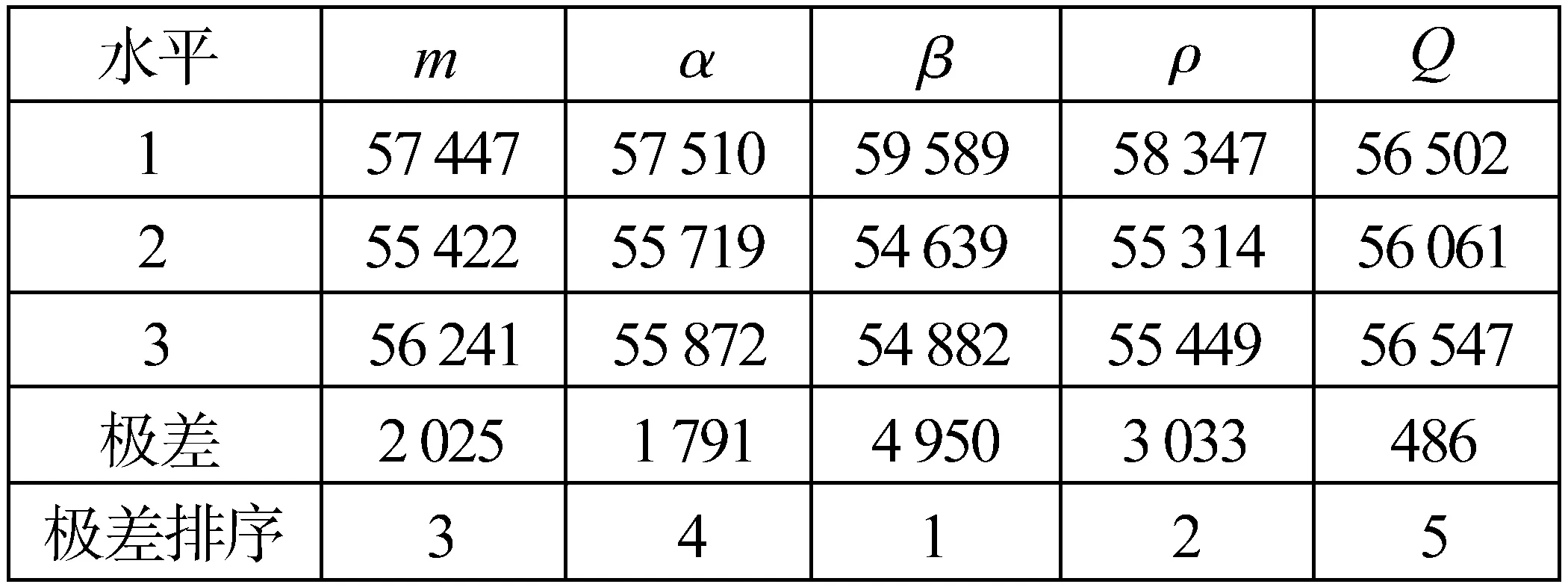
图5 数据分析

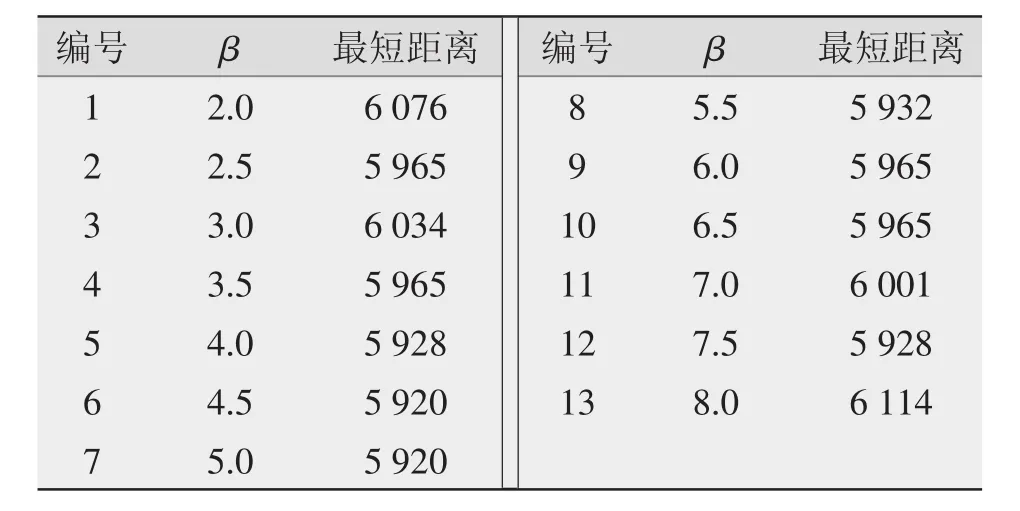
表2 回归试验数据

图6 最优值与β的散点

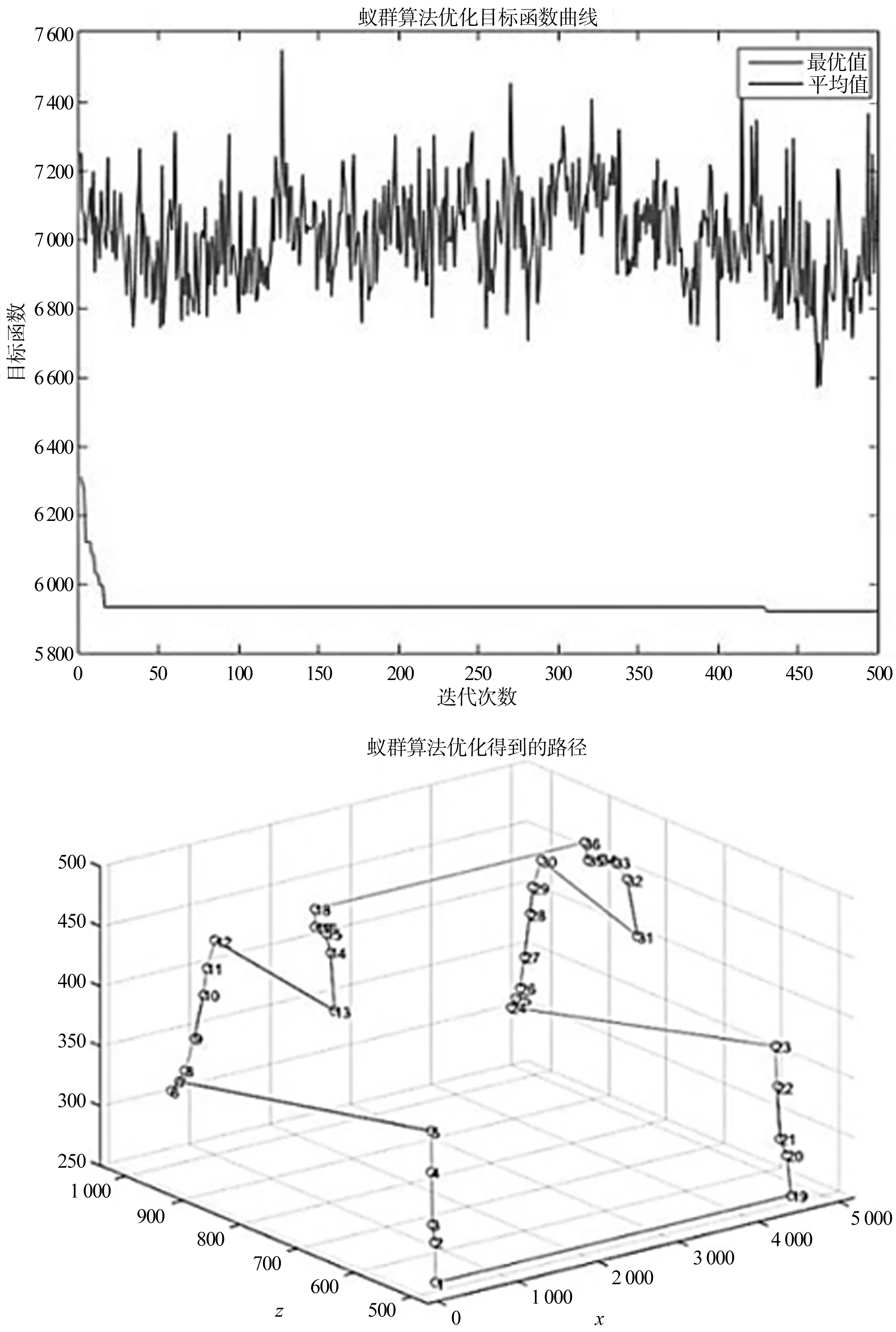
图7 路径规划

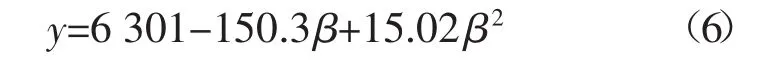
因 p（p=0.003）＜α（α=0.01），可认为回归效果显著。因β=4.5与β=5时，最优值相等，认为最优或近似最优值为5 920 mm。得到最优路径为：1—2—3—4—5—7—6—8—9—10—11—12—13—14—15—16—17—18—36—35—34—33—32—31—30—29—28—27—26—25—24—23—22—21—20—19，如图7所示。

4 结论

通过正交试验优化蚁群算法的参数，明显提高了算法性能。通过回归分析，初步探索了蚁群算法参数与求解结果之间的函数关系。结果表明，采用改进蚁群算法能够得到汽车后侧围板点焊机器人工作站的最优或近似最优路径。

[1]Dong W，Li H，Teng X.Off-line programming of Spot-weld Robot for Car-body in White Based on Robcad[C].International Conference on Mechatronics and Automation.IEEE，2007：763-768.

[2]Dorigo M，Maniezzo V，Colorni A.The Ant System：Optimization by a colony of cooperating agents[C].IEEE Transactions on Systems，Man and Cybernetics，1996：29-41.

[3]涂海宁，徐星.改进蚁群算法下的物料配送路径优化研究[J].机械设计与制造，2017（8）：265-268.

[4]何少佳，史剑清，王海坤.基于改进蚁群粒子群算法的移动机器人路径规划[J].桂林理工大学学报，2014，34（4）：765-770.

[5]吴华锋，陈信强，毛奇凰，等.基于自然选择策略的蚁群算法求解 TSP 问题[J].通信学报，2013（4）：165-170.

[6]徐练淞，潘大志.一种求解TSP问题的改进遗传蚁群算法[J].智能计算机与应用，2017，7（3）：34-36.

[7]杜衡吉，李勇.蚁群算法中参数设置对其性能影响的研究[J].现代计算机，2012（9）：3-7.

[8]魏星，李燕.蚁群算法中参数优化及其仿真研究[J].制造业自动化，2015（10）：33-35.

[9]俞云新.蚁群算法研究及其应用[D].江西：华东交通大学，2011.