一种低信噪比条件下的深空探测载波捕获算法

杜检来，方堃，刘刚，李琦

（上海航天电子有限公司，上海 201821）

0 引 言

进入21世纪以来，随着探测器成功登陆火星、土星，深空探测越来越成为全球关注的焦点[1]。深空探测作为人类认识自己、了解太阳系和宇宙起源、探索宇宙奥秘的重要途径，具有重要的科学和经济意义。在我国，随着“嫦娥工程”的成功实施，已经迈出了深空探测的第1步，而随着航天事业的发展，后续更远的火星探测计划也已经启动。

深空测控通信系统是深空探测工程的重要组成部分。它提供探测器发射和长期运行全过程的测控支持，是地面系统与深空探测器联系的唯一通道和手段[1]。而相对于地球卫星的测控通信系统，深空测控通信系统作用距离大大增加。以火星为例，其距离地球（59.6～401.3）× 106km，相当于地球静止轨道距离的1 114.72～1 655.56倍。相对于地球同步卫星，其通信路径损耗增加量最高可达64.3 dB。因此，深空通信接收的信号非常微弱，这将导致接收信号的信噪比极低，对于通信系统的载波捕获是一个巨大的挑战。

目前，针对低信噪比条件下的载波捕获算法主要有3类[7]：①基于极大似然（Maximum Likelihood，ML）或改进的ML准则估计算法；②时频分析法；③含预处理的FFT（Fast Fourier Transform）算法。传统的ML算法，是一个多维搜索的非线性优化问题，计算复杂度高，对初始值的选取要求也高，几乎无法在实际中应用。而时频分析法、现有的算法存在参数估计鲁棒性差、复杂度高、门限敏感等问题，给实际应用带来困难。故本文在传统一维FFT算法的基础上，提出了一种时分复用的二维FFT载波捕获方法，其计算简单，资源消耗较低，利于工程应用。

1 深空通信载波捕获技术

在深空测控通信系统中，接收端接收到的射频信号经过通道下变频后，变为可为基带处理的中频信号，其频率成分中包括中频、载波频偏、载波频率变化率及其更高阶变化率。在信号的捕获阶段，如不考虑载波频率二阶及以上的变化率，可以将输入信号看做是线性调频（Linear Frequency Modulation，LFM）信号。现利用载波频率线性变化模型来分析信号，其复数模型信号为

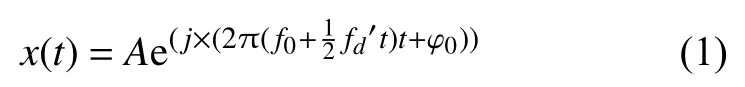
其中：A为信号幅度；为实际信号频率（包含载波频偏）；为载波频率变化率；为初始相位。

在深空通信载波捕获中，主要是采用FFT变换对载波信号进行分析，进而找出频谱峰值，完成载波捕获。在没有载波频率变化率的情况下进行FFT计算后，频谱峰值就是一个点，但当有载波频率变化率的时候，频谱峰值就不再是一个点，而是一个平台。这个平台的频域范围是其中，T为被分析的这段信号的时间长度。由于平台的存在，在深空通信中，对载波的捕获需要同时估计出载波频偏与载波频率变化率

其中：为本地载波频率；表示假设的载波频率变化率。

由式（2）可见，经过相乘后的信号仍然为LFM信号，具有LFM信号的特性。

根据Parseval定理可知，能量是守恒的，时域能量等于频域能量，不会因为变换而发生改变，故信号经过傅里叶变换后其总能量保持不变[3]。现假设LFM信号s(t)的幅频响应为S(ω)，能量为P，则可以得到等式为?

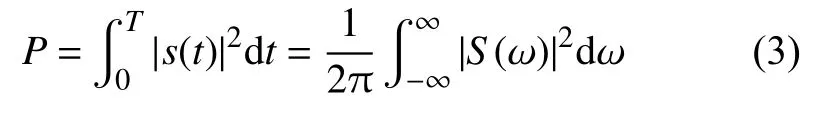
假设时间长度T和信号带宽B的乘积远大于1，则可以近似为宽度为信号带宽B的矩形。因此，可将上式右端频域能量的积分区间缩小为信号带宽范围[0，B]，S(ω)用信号频谱中心处的幅值A代替，则信号能量为

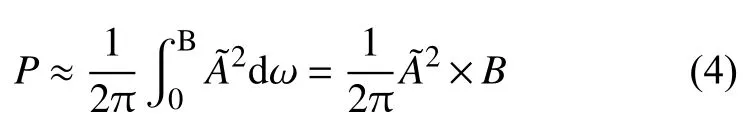
现设定LFM 信号的调频斜率为K，其中K=B/T，代入上式得

由式（5）可知，当LFM信号能量一定时，对相同的时间长度T，LFM信号频谱幅值的平方与信号调频斜率K成反比[3]。式（2）中：与越接近，值越小，对消后信号的载波频率一次变化率（调频斜率K）越小，相应输出信号的频谱峰值就越高。这样，通过搜索频谱峰值，就可得到信号载波频率（初始频率）和载波频率一次变化率（调频斜率）的估值。

2 时分复用的二维 FFT设计

由于平台的存在，要成功完成载波捕获，就需要对载波频偏与载波频率变化率两者同时进行搜索。深空通信中接收到的信号信噪比极低，为了能够成功捕获，需要对接收信号进行长时间的相干累加。此外，由于载波频偏的存在，采样频率必须足够高，这就意味着采样数据的量很大。对如此多的采样数据直接进行FFT分析几乎是不可行的，为了降低运算量，本文采用了一种时分复用的的二维FFT设计方法。

2.1 二维FFT设计

二维FFT设计的思想是：根据接收信号的载波频偏和载波频率变化率范围，将载波频偏和载波频率变化率进行二维分段，根据分段信息，对接收信号分别利用FFT进行分析，从而降低了数据处理量。该方法可以同时估计出信号的载波频偏和载波频率变化率故称为二维FFT捕获。其具体的实现方式如图1所示。

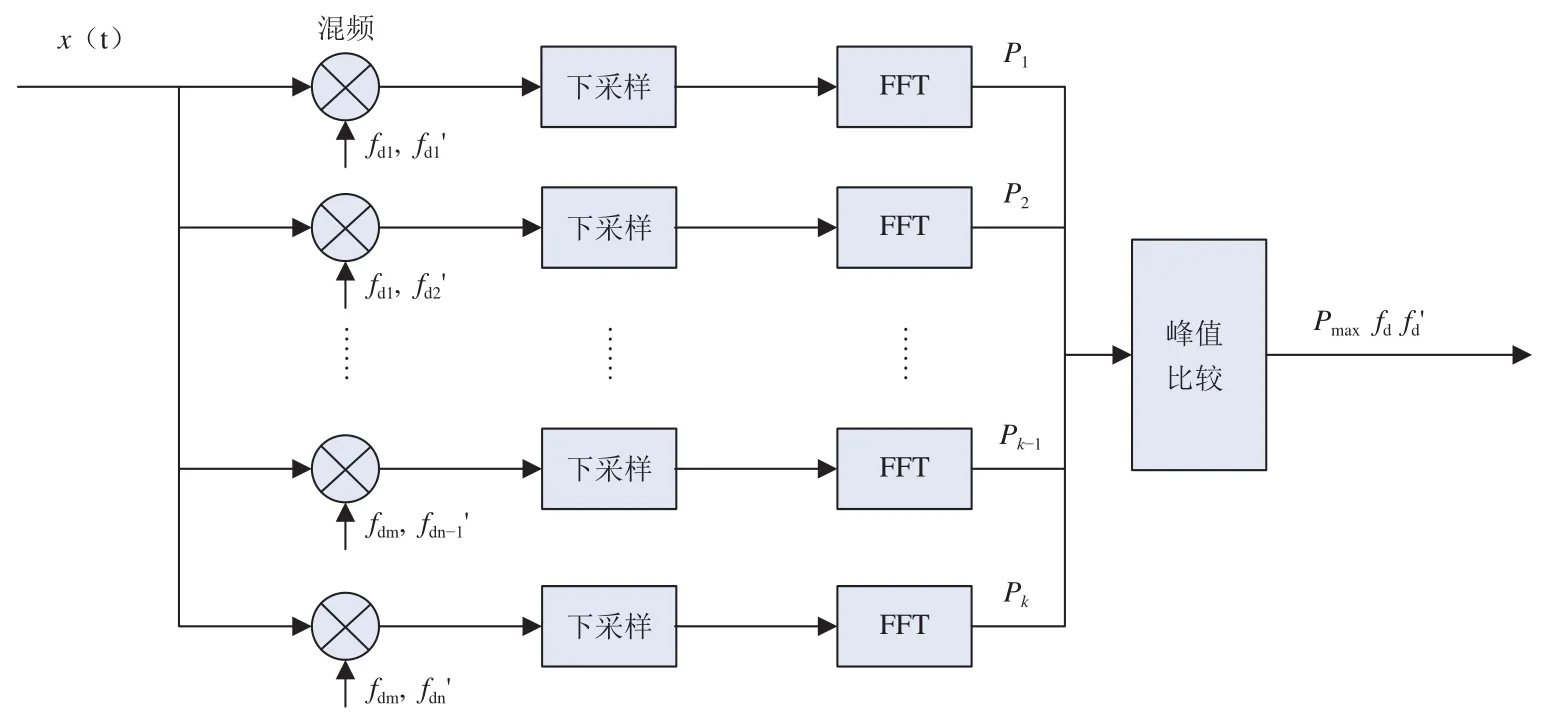
图1 二维FFT捕获图Fig.1 The capture block diagram based on 2D-FFT

假设接收信号为x(t)，接收信号载波频偏范围为载波频率变化率范围为将载波频偏按照间隔 Δfd进行分段，每段中心频率为将载波频率变化率按照间隔进行分段，每段变化率为每次根据不同的载波频偏fd和频率变化率对接收信号进行处理。

如图1所示，接收信号进入后，分别根据不同的载波频偏和频率变化率与本地载波信号进行混频，混频后的数据经过下采样滤波处理后，送入FFT模块进行处理，并寻找此区间的峰值P。多路FFT计算的峰值总计有个，通过对这K个峰值进行比较，就可以得到全部载波频偏范围和载波频率变化率范围内FFT计算的最高峰值，此峰值所在的载波频偏和载波频率变化率就是实际载波捕获的结果。

2.2 时分复用设计

在二维FFT捕获方法中，如果追求最快的捕获时间，就需要采用多路并行计算，理论上需要K个并行FFT计算模块，但是在实际应用中，利用如此多的FFT计算模块几乎是不可行的，其将消耗大量的乘法器资源，而且大量的资源消耗对器件的成本和功耗也是一个挑战。为了降低资源消耗，本文采用了一种时分复用的设计方法，其设计思想是：针对同一组采样数据，进行多次FFT运算，将并行FFT运算改为串行FFT运算，从而达到降低资源的目的。同时，在FFT运算时，采用频率较高的工作时钟，从而减少运算时间，满足捕获时间要求。其具体的实现方式如图2所示。

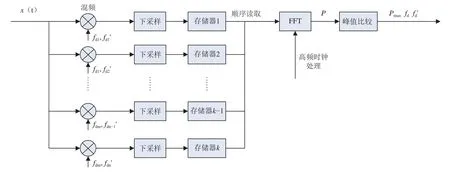
图2 时分复用FFT捕获图Fig.2 The capture block diagram based on TDM 2D-FFT

由图2可见，采样信号进入后，首先进入K个混频单元，与本地载波进行混频。混频后的信号进行下采样和滤波后，数据量大为减少，将其存入存储器中。系统按顺序从存储器中读取数据送入FFT处理模块，并得到最终的运算结果，对K次FFT运算后的数据进行比较，就可以得到运算的最高峰值，进而得到采样信号的载波频偏和载波频率变化率相对于多路并行计算，此种方法节省了K–1个FFT处理单元，降低了资源消耗。

现假设系统工作时钟为40 MHz，载波频偏分段数m为13，载波频率变化率分段数n为69，对串行FFT和并行FFT算法进行比较，比较结果如表1所示。

表1 FFT捕获算法对比Table 1 The comparison of different FFT capture algorithms

从表1中可以看出，基于时分复用的串行FFT捕获算法，其捕获时间较短、FFT计算单元消耗少，其通过将数据存入存储器，利用高频时钟串行处理的方法，有效地降低了捕获时间、降低了资源消耗。虽然增加了存储单元，但是可以通过外挂存储器，硬件片内存储器等方式解决，兼顾了性能和工程的实现。

3 仿真实验及结果

本文利用信号采集卡采集的实际的载波信号进行仿真分析，采样频率设定为40 MHz，载波中心频率为5.944 3 MHz，采样的信号载噪比最低为17 dBHz，信号载波频偏范围为[–100，100] kHz，载波频率变化率范围为[–100，100] Hz/s。

在时分复用二维FFT设计上，在载波频偏和载波频率变化率划分方面，将载波频偏（范围为[–100，100] kHz）以为步进划分为13个区间，将载波频率变化率（范围为[–100，100] Hz/s）以3 Hz/s为步进划分为69个离散值；在系统处理方面，系统工作时钟为40 MHz，二次采样频率为16 kHz。

在设计中，为了后续载波跟踪的需要，捕获的载波误差需要控制在一定范围之内。在本文中，考虑到捕获时间和存储器大小，载波频偏的划分步进为16 kHz，二次采样频率为16 kHz。而对于FFT点数，在相同的采样频率下，点数越高，其灵敏度越高，频率分辨精度越高。在载噪比为23 dBHz条件下，利用FFT对载波信号进行了分析。

如图3所示，利用4 096点FFT进行分析时，频率分辨精度为3.9 Hz，得到的峰均比为14.2 dB；利用16 384点FFT进行分析时，频率分辨率为1 Hz，得到的峰均比为20.6 dB。故在条件允许的情况下，FFT的计算点数越高越好。考虑到深空条件下载波信号微弱及后续载波跟踪的需要，选取FFT计算点数为16 384。

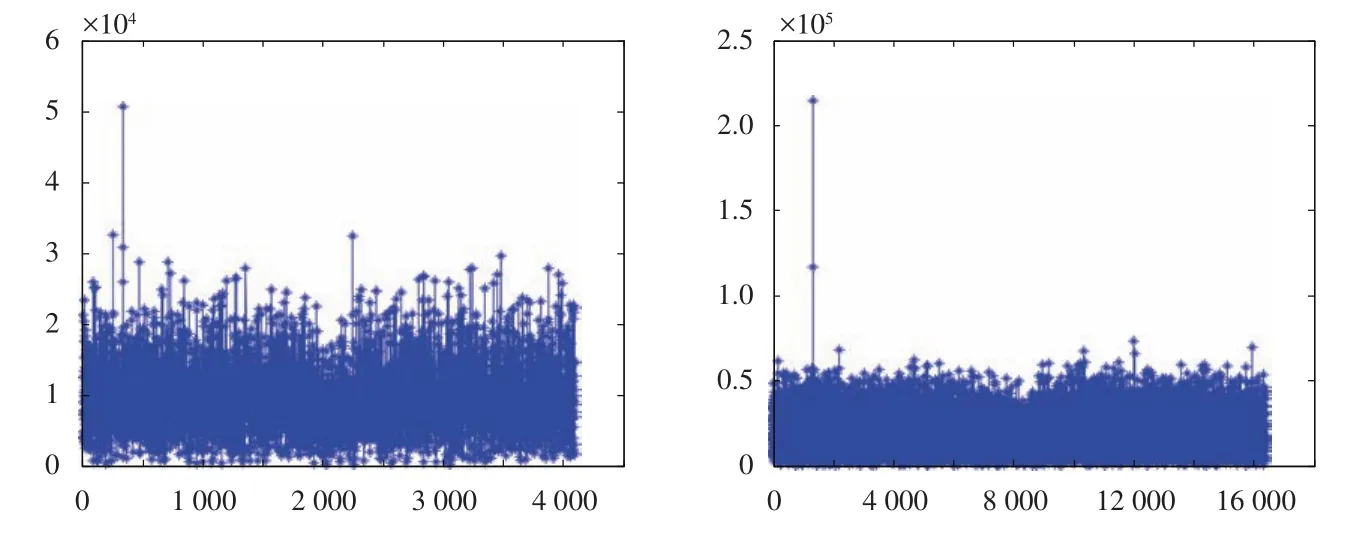
图3 4 096点及16 384点FFT对比图Fig.3 The comparison between 4 096-point and 16 384-point FFT

采样信号载噪比为19 dBHz，多普勒扫频起始频偏为49.641 kHz，频率变化率为–40 Hz/s，采用前述的捕获方法对采样信号的载波频偏和频率变化率进行二维搜索所得的FFT 幅值如图4～5所示。

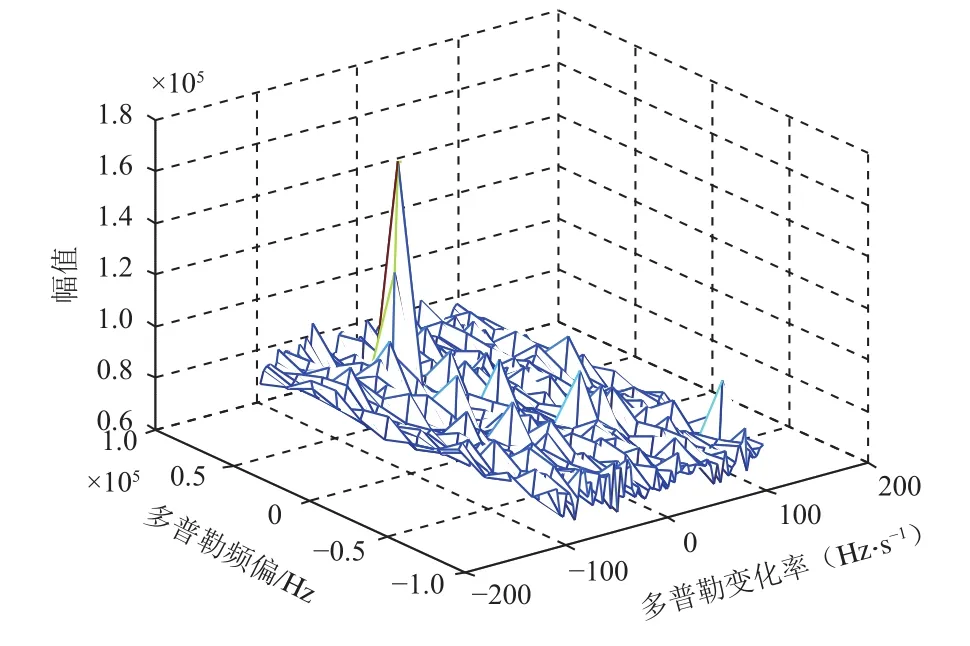
图4 时分复用二维FFT捕获仿真图Fig.4 The capture simulation diagram based on TDM 2D-FFT

由图4可见，FFT的峰值出现在频率区段[40，56]kHz和频率变化率为–39 Hz/s的交汇处。而从图5可以看到，实际捕获的频偏为49.641 kHz，这与设定的信号一致，表明本文提出的捕获方法正确。

在不同的设定条件下，对采样信号进行仿真，采用本文所述捕获策略对接收信号进行捕获，捕获及分析结果如表2所示。

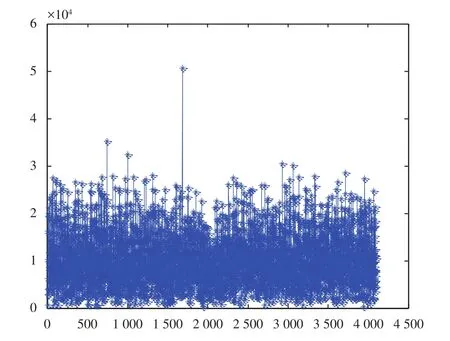
图5 最大峰值区间FFT分析图Fig.5 FFT analysis chart of the maximum peak interval

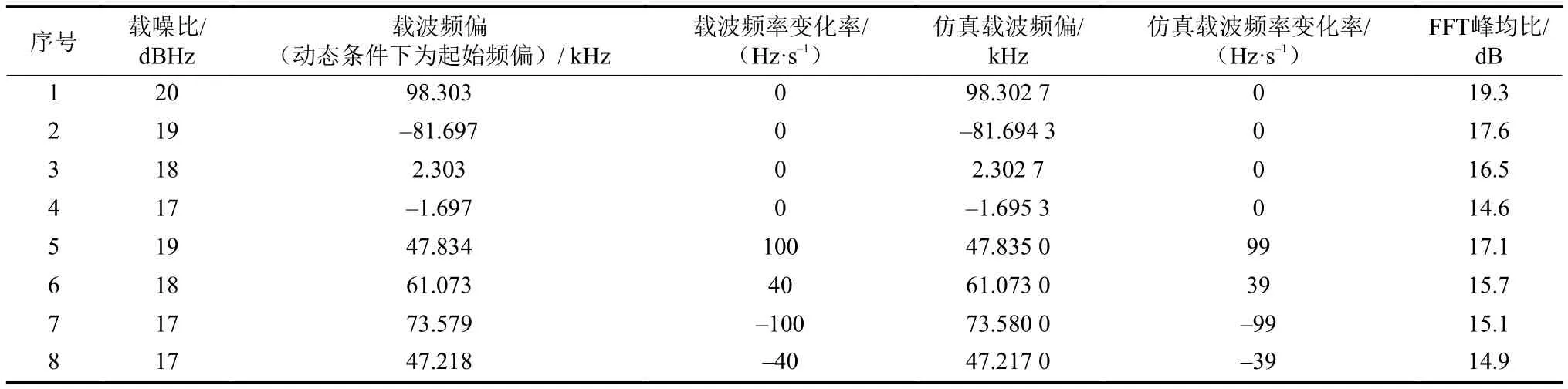
表2 采样信号捕获分析结果Table 2 Analysis results of the sampled signal's capture

从表2可以看出，在低信噪比条件下，在信号载波频偏范围是[–100，100] kHz，载波频率变化率范围是[–100，100] Hz/s条件下，捕获算法均能够正确捕获。而根据我们的实际分析，载波频率捕获精度达到3 Hz，载波频率变化率精度达到1.5 Hz/s，捕获信号载噪比最低可达17 dBHz，捕获所需时间在2 s之内。另外，由于采用分段二维捕获方式、时分复用方式，该捕获算法能够有效降低捕获资源，利于工程实现。

4 结束语

本文提出了一种时分复用的二维FFT载波捕获算法。其基于对载波频率和频率变化率区间进行分段来进行二维FFT搜索，有效地降低了载波捕获的运算量。同时，采用一种时分复用的实现方式，有效地降低了资源消耗，利于工程实现。通过仿真表明，此捕获方法满足了深空条件下低信噪比载波捕获的要求，能够在2 s时间内，对载噪比最低达17 dBHz的载波信号进行捕获，具有实际的应用价值。同时，该捕获算法也可用于其它低信噪比条件下的载波捕获场合中，适应性广。

[1]董光亮.深空测控新技术研究进展[J].深空探测学报，2014，1（4）：243-250.DONG G L.Development of new technology in deep space TT&C[J].Journal of Deep Space Exploration，2014，1（4）：243-250.

[2]于志坚.深空测控通信系统[M].北京：国防工业出版社，2009：11-12.YU Z J.Deep space TT&C system[M].Beijing：National Defend Industry Press，2009：11-12.

[3]卢满宏，李晓亮，黄建国.深空测控通信载波信号二维FFT捕获技术[J].飞行器测控学报，2013，32（4）：311-315.LU M H，LI X L，HUANG J G.Two-dimension FFT carrier signal acquisition technology in deep space TT&C communication system[J].Journal of Spacecraft TT&C Technology，2013，32（4）：311-315.

[4]方轶，高磊，王灵，等.一种高灵敏度深空应答机载波捕获算法[J].上海航天，2015，32（2）：32-37.FANG Y，GAO L，WANG L，et al.A carrier acquisition algorithm of high sensitivity DST[J].Aerospace Shanghai，2015，32（2）：32-37.

[5]甘浩，张哓林，马月红，等.一种改进的深空高动态微弱信号频率捕获算法[J].遥测遥控，2015，36（4）：6-11.GAN H，ZHANG X L，MA Y H，et al.An improved frequency acquisition algorithm for high dynamic and weak signal in deep space[J].Journal of Telemetry，Tracking and Command，2015，36（4）：6-11.

[6]韩孟飞，崔嵬，王永庆，等.极低载噪比高动态信号的捕获策略研究与仿真[J].系统仿真学报，2009，21（23）：7589-7592.HANG M F，CUI W，WANG Y Q，et al.Study and simulation of acquisition technique for extremely low-CNR high-dynamic signals[J].Journal of System Simulation，2009，21（23）：7589-7592.

[7]焦健，张钦宇，李晖.深空通信中基于FFT的高动态扩频信号的捕获[J].电讯技术，2007，47（6）：40-43.JIAO J，ZHANG Q Y，LI H.Acquisition of high dynamics signal based on FFT in deep space communication[J].Telecommunication Engineering，2007，47（6）：40-43.

[8]段瑞枫，刘荣科，周游，等.一种低复杂度的极低信噪比高动态信号载波粗捕获算法[J].航空学报，2013，34（3）：662-669.DUAN R F，LIU R K，ZHOU Y，et al.A low-complexity coarse carrier acquisition algorithm for signals with extremely low signal noise ratio and high dynamics[J].Acta Aeronautica et Astronautica Sinca，2013，34（3）：662-669.

[9]KINMAN W.Doppler tracking of planetary spacecraft[J].IEEE Transactions on Microwave Theory and Techniques，1992，40（6）：1199-1204.

[10]BERNER J B，WARE K M.An extremely sensitive digital receiver for deep space satellite communications[C]//Eleventh Annual International Phonic Conference on Computers and Communications.Scottsdale，Arizona：IEEE，1992.