青海省五龙沟地区化探金异常下限确定方法探讨

邱 瑜， 田 滔， 沈 骁， 杨言辰

(1.青海省第五地质矿产勘查院，西宁 810028；2.吉林大学 地球科学学院，长春 130026)

0 引言

在地球化学勘查中，异常下限的确定是最基本也是最重要的问题之一[1-2]。从众多的化探数据中提取地球化学异常，异常下限的确定直接地影响异常提取和识别效果[3]。合理的确定异常下限，对于找矿靶区的圈定有着至关重要的意义，并对后期的异常查证有直接地影响，在矿产勘查和预测中占有十分重要的地位[4]。

通常认为地质体中常量元素服从正态分布，微量元素服从对数正态分布。但通过近年来的研究发现，元素含量在地质体中的空间分布是不均匀的，往往与地质体的几何形态、埋藏深度以及周围地质体的作用有关，表现为地球化学场的空间自相似性或统计自相似性。这使得元素的地球化学背景和异常与地质等因素联系起来呈现出幂指数关系，表现为多重分形分布。成秋明等[5-6]研究指出，与矿化有关的微量元素地球化学异常服从多重分形分布，而背景则服从正态或对数正态分布。因而我们可以利用分形方法来处理区域地球化学数据，这不仅考虑了各种不确定因素导致的数据的空间变化，而且考虑地球化学数据场在大范围空间内自相似性的特点[7- 10]。

东昆仑地区是青海省乃至全国主要的金、铜、铁多金属成矿区之一[11]。自上世纪80年代发现五龙沟大型金矿床以后，随着国家找金热潮的涌现，后期又在该带内发现了大场、纳赤台、开荒北、果洛龙洼、东大滩、加给陇洼等多处大中型金矿床[12]，表明该区域具有巨大的找金矿潜力。因此，以五龙沟地区作为研究对象，开展东昆仑地区金元素异常下限取值方法探讨研究，具有很好的代表性。

1 试验区地质特征

五龙沟金矿集中区位于青海省海西州都兰县境内，地处东昆仑东段中东部，大地构造位置属于东昆中岩浆弧带。区域内出露地层主要有古元古代长城纪金水口群、中元古代小庙群以及晚元古代青白口纪丘吉东沟组，其中又以金水口群地层为主，岩性为黑云斜长片麻岩、黑云角闪斜长片麻岩、斜长角闪岩、石英片岩和大理岩组合[13]，是一套中、高级变质岩系。区内断裂构造主要有昆中与昆北断裂带，均呈近东西向展布，近平行的北西向脆韧性剪切带发育其中[12,14]。区域内岩浆活动频繁，多期次不同岩性的岩浆岩广泛发育，发育时代主要为晋宁期、印支期，岩性以中酸性的花岗闪长岩、二长花岗岩、钾长花岗岩为主。金矿化带沿NW向和近SN向脆性断裂带展布，金矿床赋存其中(图1)。目前发现大型岩金矿床1处(深水潭金矿床)，中型岩金矿床1处(石灰沟金矿床)，小型金矿床4处(淡水沟、红旗沟、中支沟、打柴沟金矿床)。

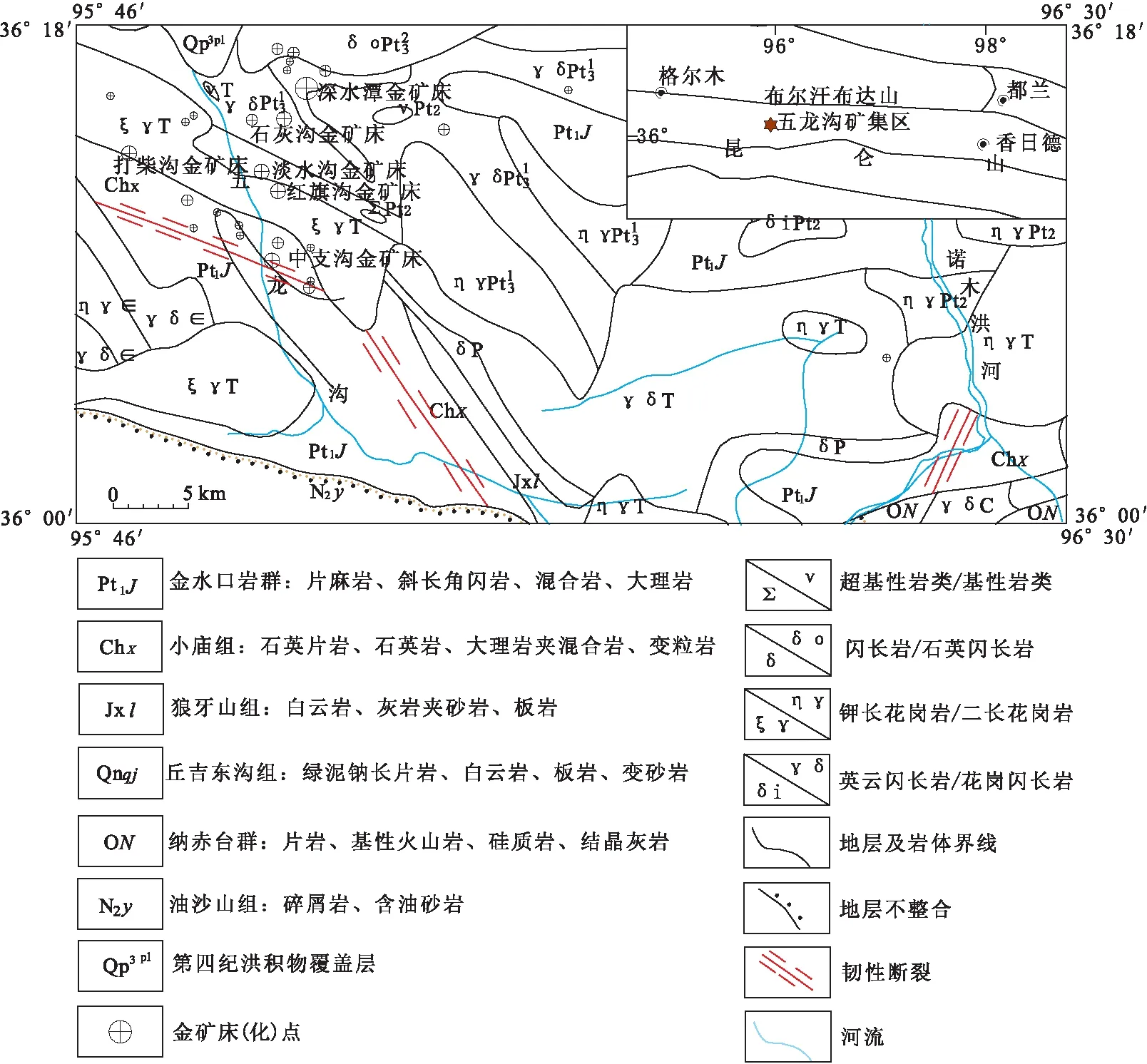
图1 研究区地质矿产示意图Fig.1 The study area map of geology and mineral resources

2 金异常下限确定方法

2.1 数据来源

本次研究数据来自《青海省都兰县五龙沟地区J46E023024等十一幅1∶50 000水系沉积物地球化学测量及地面高精度磁法测量》项目7 851个水系沉积物样品测试数据，采样粒级为-10—+60目，采样密度平均4个样/km2。该项目由河南省地质矿产勘查开发局地球物理勘查队2010年完成。

2.2 金异常下限确定方法

2.2.1 传统方法

传统的地球化学元素异常下限求取，是先对区域内取得的化探数据进行概率分布检验，看其是否符合对数正态分布。如果分析数据满足对数正态分布，则可以根据数据的背景值加两倍标准离差直接计算得到元素异常下限。否则就对全域数据集进行离群点迭代处理，把均值加减三倍离差范围外的数据剔除，直到无离群数值可剔除为止，形成背景数据集，然后用背景数据集的均值加两倍标准离差作为元素的异常下限[7-8]。

对五龙沟地区1∶50 000水系沉积物测量Au数据统计分析发现(表1)，不符合标准的对数正态分布。对数据进行离群点的迭代处理后，确定金异常下限为1.9×10-9。

表1 五龙沟地区金元素地球化学参数统计表

2.2.2 含量—频数分形法

含量—频数分形法，其原理是将元素含量(C)按指数从小到大划分出若干个不同级别，分别统计不同含量(C)区间对应的数据个数之和(N)，然后在对数坐标图中采用分形原理计算出元素的异常下限。图2反映五龙沟地区1∶50 000水系沉积物测量金含量与相对组成个数的幂律关系，图2中红色实心圆点所对应的含量值即为元素的异常下限值。

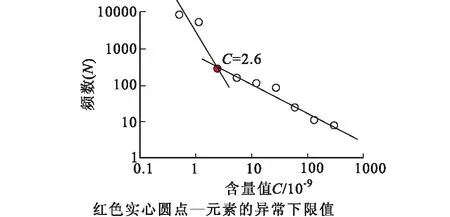
图2 含量—频数分形法确定金元素异常下限幂律图解Fig.2 Power-law diagram for the determination of gold’s anomaly lower threshold using the content-frequency fractal method

2.2.3 含量—总量分形法

含量—总量分形法中统计的数据个数(N)为大于某一含量(C)的元素总量除以其对应级别的元素含量(C)，图3反映五龙沟地区1∶50 000水系沉积物金元素的含量与含量总量值的幂律关系。

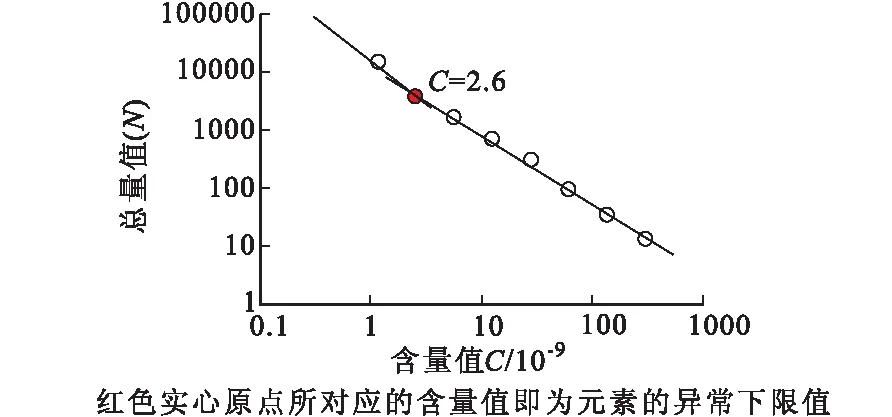
图3 含量—总量分形法确定金元素异常下限幂律图解Fig.3 Power-law diagram for the determination of gold’s anomaly lower threshold using the content-sum fractal method

2.2.4 含量—面积分形法

地球化学数据分布与尺度之间遵循一定的幂率关系[5-6,9]。陈秋明等[5-6]结合分形理论提出了确定地球化学异常的含量—面积分形方法。地球化学元素含量-面积的分形分布服从方程

C=kAa

(1)

式中：C为元素含量；k为常数；A代表大于含量C的面积；a是与最大奇异指数有关的指数，即分维数。

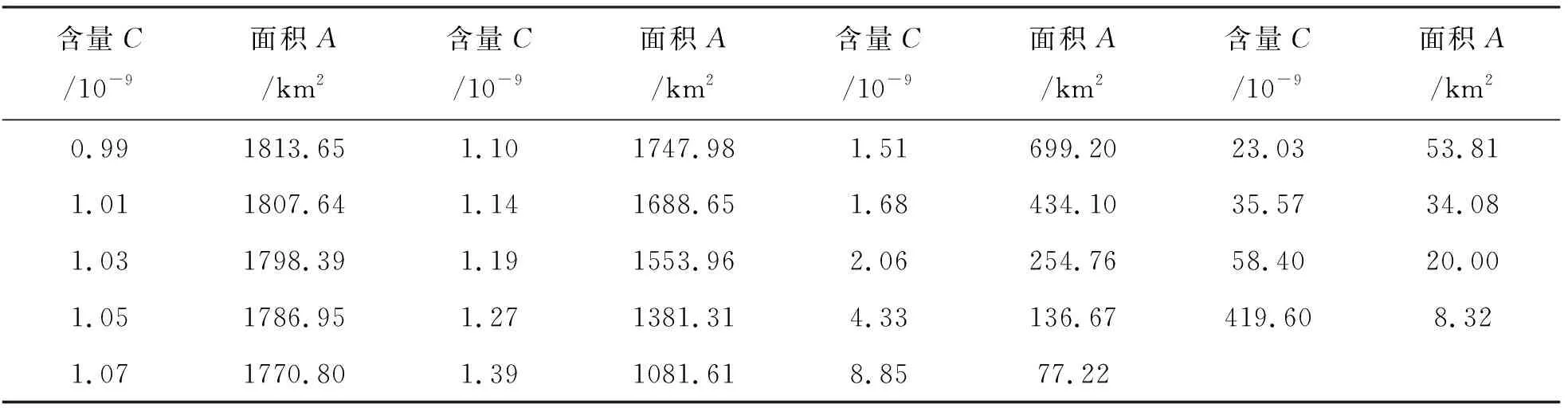
这里我们用GeoExpl软件对五龙沟地区的地球化学数据进行处理，首先将离散数据变为网格化数据，然后按累频得出金元素异常含量分界点，最终生成Au地球化学图。将不同含量值的图层进行分离，计算其相应的异常面积。金异常含量和异常面积的对照见表2。

应用表2的数据,在lg(C)—lg(A)双对数坐标系中投点，用最小二乘法拟合二段直线(图4)，得到相应的直线方程为:

lg(A)=-2.7753lg(C)+3.3332

(C<4.33)

lg(A)=-0.6193lg(C)+2.5018

(4.33≤C<419.6)

(2)

两个区间的剩余平方总和(E=E1+E2)为0.069,公式(2)通过显著性检验。分界点C为4.33×10-9，该值保留一位小数得到金异常下限值4.3×10-9。

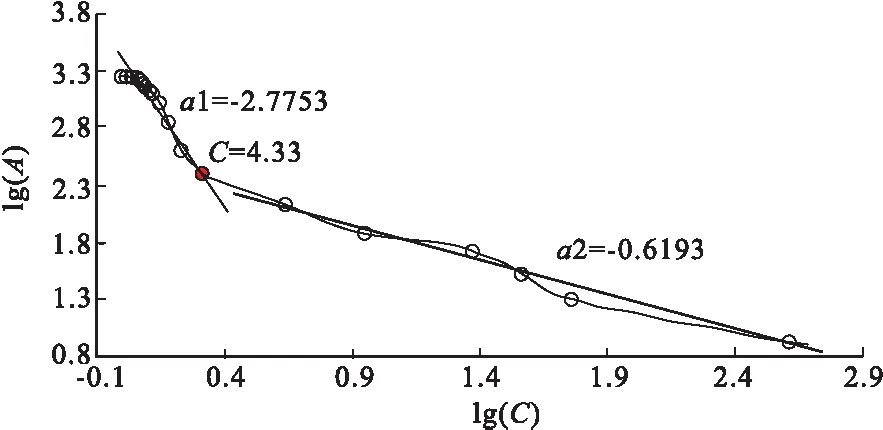
图4 五龙沟地区金元素lg(C)—lg(A)线性拟合图Fig.4 log(C)-log(A) plots for Au element in Wulonggou area

含量C/10-9面积A/km2含量C/10-9面积A/km2含量C/10-9面积A/km2含量C/10-9面积A/km20.991813.651.101747.981.51699.2023.0353.811.011807.641.141688.651.68434.1035.5734.081.031798.391.191553.962.06254.7658.4020.001.051786.951.271381.314.33136.67419.608.321.071770.801.391081.618.8577.22

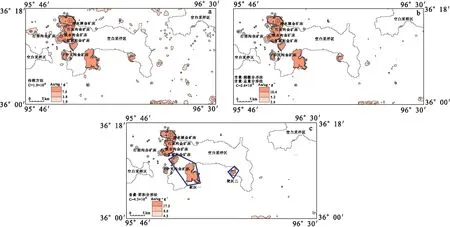
图5 五龙沟矿集区不同方法异常下限圈定的Au异常对比图Fig.5 Au anomaly contrast figure based on threshold determined by different methods in Wulonggou ore concentration area(a)传统方法；(b)含量-频数分形法，含量-总量分形法；(c)含量-面积分形法

3 不同方法确定金异常下限

传统方法确定的Au异常下限为1.9×10-9,含量—频数分形法和含量—总量分形法确定的Au异常下限为2.6×10-9,含量—面积分形法确定Au异常下限为4.3×10-9。用三种不同分形方法确定的金异常下限，均比传统方法确定的异常下限值要高，且含量—面积分形法得到的金元素异常下限变化幅度更大，超过传统方法的两倍。五龙沟金矿集区是金的强富集区域，金背景值应该是相对其他区域偏高的。传统方法将过多的高值数据剔除，导致金元素异常下限偏低。分形方法考虑了异常分布与尺度的关系，消除了人为剔除高、低值数据的干扰，特别是矿集区内特高含量数据的影响，应该说分形方法得到异常下限值的提高是可以预见的，也是相对合理的。不同异常下限值圈定的研究区异常分布状况见图5。

从图5可以清楚地发现，四种方法确定的金异常下限所圈定的异常，均与大部分小型以上金矿床产出位置吻合较好(打柴沟小型金矿床除外)。同时，随着异常下限值的提高，异常面积有了明显地减小，以含量—面积分形法对异常面积的减小尤为明显。

图5(b)中,含量—频数分形法和含量—总量分形法确定的金异常下限，考虑了元素含量与频数的对应关系，计算十分简便，可以用GeoExpl软件分形计算功能直接求出。这两种方法确定的金异常下限相近，比传统方法确定的异常下限稍高，从而减小了异常面积，对后期的异常查证工作区域的缩小有利。

图5(c)中,含量—面积分形法在前两种分形理论的基础上，考虑了异常的空间形态及形态的自相似性和随尺度的变化性。含量—面积分形法异常下限值的求取过程相对繁琐，得到的元素异常下限值更高，进一步缩小了异常面积，更好地突出高强度异常，缩小了异常区域面积，达到迅速定位靶区的目的。

四种方法确定的金异常下限圈定的异常，对打柴沟小型金矿床和区内大多数金矿点和矿化点反映较差，特别是打柴沟金矿床至中支沟金矿床一线韧性断裂带部位出露的金矿点、矿化点。这从侧面反映出本次水系沉积物测量工作的局部采样质量存在问题。

对图5中不同方法确定的金异常下限圈定的金异常对比分析，最终利用含量—面积分形法得到的异常圈定出两处金矿找矿靶区(图5(c))。这两处靶区内金异常强度很高，均具有三级异常浓度分带且未发现金矿床点，可以作为后期找矿的重点区域。

4 结论

从寻找小型以上金矿床的角度出发，在五龙沟矿集区，分形方法(特别是含量—面积分形法)得出的金异常下限圈定的异常，漏矿的风险不会太大；且大大缩小了异常查证的范围，从而达到快速高效的实现地质找矿重大突破。因此，在五龙沟为代表的东昆仑地区找寻金矿的工作中，采用分形方法确定金异常下限是可行的。

参考文献：

[1] 李随民,姚书振.基于MAPGIS的分形方法确定化探异常[J].地球学报,2005，26(2):187-190.

LI S M,YAO S Z.The determination of thresholds by the fractal method based on MAPGIS[J].Acta Geoscientica Sinica,2005,26(2):187-190.(In Chinese)

[2] 韩东昱,龚庆杰,向运川.区域化探数据处理的几种分形方法[J].地质通报,2004，27(7):714-719.

HAN D Y,GONG Q J,XIANG Y C.Some new fractal methods for regional geochemical survey data processing[J].Geological Bulletin of China,2004,27(7)：714-719. (In Chinese)

[3] 吕文超,周永章,张焱,等.钦杭成矿带南段文地幅水系沉积物地球化学异常识别[J].中山大学学报( 自然科学版),2012，51(5):107-112.

LV W C,ZHOU Y Z,ZHANG Y,et al.Geochemical anomaly identification of stream sediments of Wendi sheet in the south segment of the Qinzhou-Hangzhou metallogenic belt[J].Acta Scientiarum Naturalium Universitatis Sunyatseni,2012,51(5):107-112.(In Chinese)

[4] 孙忠军.矿产勘查中化探异常下限的多重分形计算方法[J].物探化探计算技术,2007，29(1):54-57.

SUN Z J. Multifractal method of geochemical threshold in mineral exploration[J].Computing Techniques For Geophysical and Geochemical Exploration,2007,29(1):54-57.(In Chinese)

[5] 成秋明.多维分形理论和地球化学元素分布规律[J].地球科学,2000，25(3):311-318.

CHENG Q M.Multifractal theory and geochemical element distribution pattern[J].Earth Science,2000,25(3):311-318.(In Chinese)

[6] 成秋明.空间模式的广义自相似性分析与矿产资源评价[J].地球科学,2004，29(6):733- 743.

CHENG Q M.Quantifying the generalized self-similarity of spatial patterns for mineral resource assessment[J].Earth Science,2004,29(6):733- 743.(In Chinese)

[7] 徐明钻,朱立新,马生明,等.多重分形模型在区域地球化学异常分析中的应用探讨[J].地球学报，2010，31(4):611-618.

XU M Z, ZHU L X,MA S M,et al.A tentative discussion on the application of multi-fractal models to the analysis of regional geochemical anomalies[J].Acta Geoscientica Sinica,2010,31(4):611-618.(In Chinese)

[8] 张磊,申维.分形方法在澳大利亚新南威尔士地区地球化学异常下限确定中的应用[J].地质通报,2009，28(2)：245-249.

ZHANG L,SHEN W.Application of fractal method in lower threshold definition of geochemistry anomaly in New South Wales area,Australia[J].Geological Bulletin of China, 2009,28(2)：245-249.(In Chinese)

[9] 娄德波,肖克炎,左仁广,等.分形滤波技术在新疆黄山-镜儿泉镍铜成矿带中的应用[J].地球学报,2012,33(1):83-90.

LOU D B,XIAO K Y,ZUO R G,et al.The application of fractal filtering technique to the study of the Huangshan-Jing'erquan Ni-Cu metallogenic belt, Xinjiang[J]. Acta Geoscientica Sinica,2012,33(1):83-90.(In Chinese)

[10] 张建,王登红,孙宝生,等.基于分形理论的成矿空间分析——以新疆东天山康古尔塔格金矿带为例[J].地球学报,2009，30(1):58-64.

ZHANG J,WANG D H,SUN B S,et al.Metallogenic spatial analysis based on fractal theory: a case study of the kangguertage gold ore belt in Xinjiang[J].Acta Geoscientica Sinica,2009,30(1):83-90.(in Chinese)

[11] 田承盛.东昆仑中段五龙沟矿集区金矿成矿作用及成矿预测研究[D].北京：中国地质大学，2012.

TIAN C S.Research on gold mineralization and metallogenic prognosis in Wulonggou ore concentration areas of east Kunlun middle part[D].Beijing: China University of Geosciences,2012.(In Chinese)

[12] 赵俊伟.青海东昆仑造山带造山型金矿床成矿系列研究[D].长春：吉林大学，2008.

ZHAO J W.Study on orogenicgold mettallogenic series in eastern Kunlun orogenic belt,Qinghai province[D].Changchun:Jilin University,2008.(In Chinese)

[13] 张雪亭,杨生德,杨站君.青海省大地构造图说明书[R],青海省地质图说明书[R].青海省地质矿产勘查开发局,2005.

ZHANG X T,YANG S D,YANG Z J.Geotectonic map instruction of Qinghai province[R].Qinghai Provincial Bureau of Geominerals Exploration,2005.(In Chinese)

[14] 李厚民,沈远超,胡正国,等.青海东昆仑五龙沟金矿床成矿条件及成矿机理[J].地质与勘探,2001，37(1):65-69.

LI H M,SHEN Y C,HU Z G,et al.Minerogenetic mechanism and condition of Wulonggou gold deposit in east Kunlun mountains,Qinghai province[J].Geology And Prospecting,2001,37(1):65-69.(In Chinese)