复电阻率法二维正演并行计算研究

张志勇 , 谭捍东, 王春阳， 汪 茂， 何中波， 梁 鹏

(1.核工业北京地质研究院中核集团铀资源勘查与评价技术重点实验室，北京 100029；2.中国地质大学(北京) 地球物理与信息技术学院，北京 100083;3.中水东北勘测设计研究有限责任公司，长春 130021)

0 引言

复电阻率法(CR)又称为谱激发极化法(SIP)是以岩矿石电阻率的频谱特性差异为基础，通过观测大地的视复电阻率频谱或激发极化场的衰减曲线，来寻找极化目标体的一种电法勘探方法[1]。相对其他电法勘探分支方法，复电阻率法有以下优点：①该方法能得到多个电性参数的信息，结合这些参数的对比解释可提供更丰富的地电信息；②采用轻便的采集装备，使其在复杂地形地区开展勘探工作更有利。目前，复电阻率法已成功应用在固体矿产勘探[2-4]、水文地质[5]、油气资源[6]、监测环境[7]、工程地质[8]等方面。

目前计算机技术发展迅速，将MPI等并行计算技术引入到地球物理数值模拟中是当前研究热点。当网格剖分单元较多，多发射源、多频率的情况下，完成复电阻率法二维有限元数值模拟需要的计算时间较长，因此有必要开发复电阻率法二维正演并行算法来提高其计算效率。

1 MPI简介

MPI(Message Passing Interface)是一个“库”而非一门语言，其具有C++和FORTRAN90的函数调用接口[9]。笔者采用Fortran和MPICH2相结合的开发工具编写并行程序。

MPI程序设计包含两种并行模式：①主从模式；②对等模式[10](图1)。

1)主从模式，也就是在所有进程中定义其中的一个作为主进程，除主进程外的所有进程都当作子进程。通过主进程可以进行广播数据或发送数据等一系列操作，同时也可以将分配好的任务分发给子进程。等到所有的子进程都完成计算以后，主进程通过收集操作从每个子进程得到任务结果，然后再看是否需要下一步的操作。

2)对等模式，就是所实现的MPI程序中各个进程间的计算量和功能大体一致。

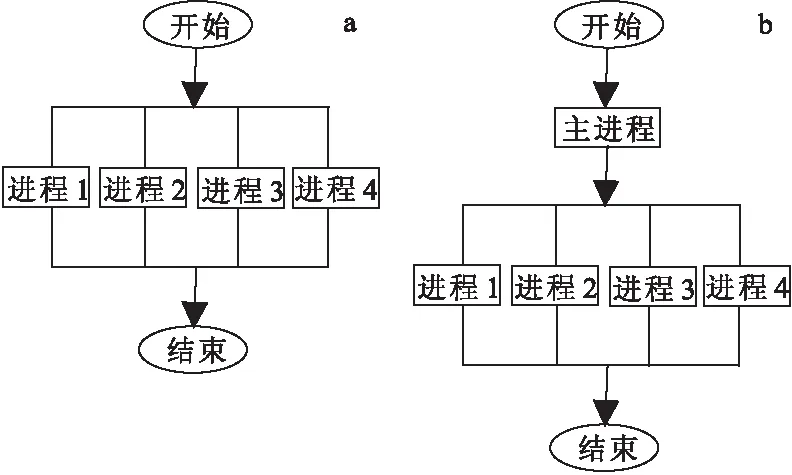
图1 并行模式分类Fig.1 Parallel mode classification(a)对等模式；(b)主从模式

2 复电阻率法二维正演

2.1 二维数值模拟

二维地电模型如图2所示，其中构造走向方向为y轴，假设其电性参数仅仅在x-z平面是变化的而沿y轴方向不变。

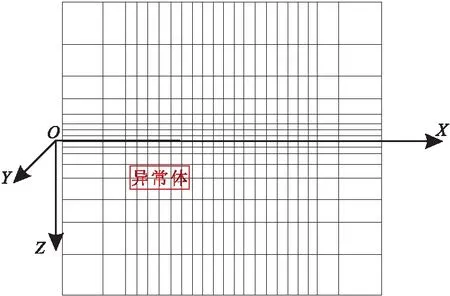
图2 二维地电模型示意图Fig.2 2D geoelectric model

假设时间因子是eiωt，忽略位移电流的影响，二次场满足的麦克斯韦方程组为[11]

(1)

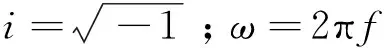
傅里叶变换

(2)

沿走向方向对式(1)作傅里叶变换，整理后得到波数域中满足的麦克斯韦方程组

(3)

(4)

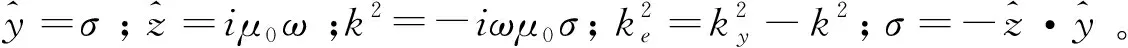
利用四节点的等参单元法进行数值模拟，将式(3)和式(4)分别运用伽里金法、格林公式，且正演使用第一类边界条件(边界网格上的电磁场值为零)，可以得到本文二维数值模拟满足的有限单元法计算公式[12-16]：

(6)

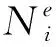
2.2 Cole-Cole模型

为同时考虑激电效应和电磁效应，将大地的实际电阻率由Cole-Cole模型定义得到的复电阻率替换。Pelton等[17]通过对大量岩石、矿石标本的一些研究，总结出就均匀岩石、矿石而言，它们的复电阻率频谱可以用Cole-Cole模型来表示。

(7)

其中:ρ(iω)是复电阻率；m是极化率；ρ0是零频电阻率；τ是时间常数；c是频率相关系数。

2.3 有限单元计算公式

引入Cole-Cole后，通过单元分析和系数矩阵存储，最终正演计算形成的矩阵方程可写成如下形式

(8)

k1(i,j)=

(9)

(10)

(11)

k4(i,j)=

(12)

(13)

(14)

2.4 矩阵的压缩存储

正演矩阵方程(8)中；左端项系数矩阵K是稀疏且对称的，全部存储K矩阵需要的内存较大。由于矩阵K每行的非零元素个数有限，充分利用这个特点，可以有效地节约内存空间。结合有限单元法的特点，单元分析时每个节点仅与其周围的几个节点参与运算。以笔者采用的4节点等参单元为例，最终形成的矩阵中每行最多只有18个非零元素，在网格剖分后，可根据有限元单元分析特点得到非零元素的行列号。采用CSR(按行压缩存储)方法，通过三个一维向量就可完成矩阵的存储，便于使用共轭梯度法来求解方程组。

2.5 求解方程组

正演形成的方程组采用林绍忠[18]介绍的SSOR—PCG(对称逐步超松弛预处理共轭梯度法)方法解方程。

解形如Ax=b的方程时，SSOR法的预处理矩阵M为：

M=(2-ω)-1(D/ω+L)(D/ω)-1(D/ω+L)T

(15)

其中:D为A的对角阵;L为A的严格下三角矩阵;ω为松弛因子，本文中将松弛因子取为“1”，初始x为零向量。那么迭代格式可以简化为

(16)

2.6 正演正确性验证

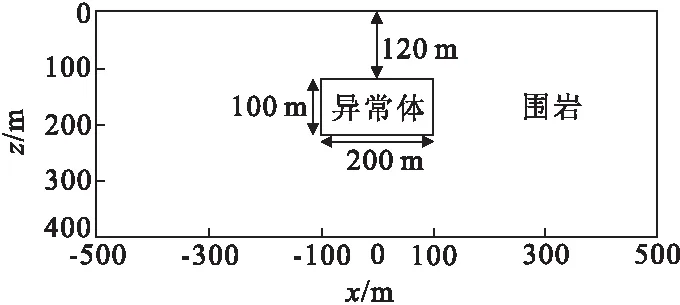
图3 二维棱柱体模型Fig.3 Two-dimensional prism model

3 二维正演并行算法总体设计

在对开发的复电阻率法二维正演串行程序深入分析后，可以发现正演中，其大部分计算时间都花费在频率循环部分求解电磁场值上面，每个发射源对应频率的方程组的求解等都是相互独立的且互不影响的，并行性较好，因此我们采用主从模式，基于多发射源和多频率来实现正演并行计算，并对其并行效率进行分析。并行的基本思路是：①将MPI环境初始化MPI_INIT( )；②主进程读入所需的参数文件；③主进程广播数据到各子进程MPI_Bcast( )；④各进程分别计算自己的任务；⑤主进程收集和整理所有进程的结果MPI_GATHERV()；⑥结束MPI并行环境MPI_FINALIZE( )[19-21]。

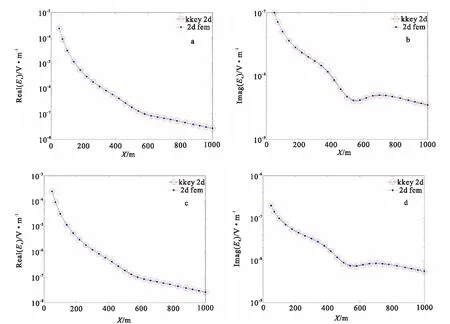
图4 二维棱柱体模型计算得到Ex实虚部对比曲线Fig.4 The Ex response comparison between the 2D finite element results and the results from 1DCSEM(a)f=8.0 Hz; (b)f=8.0 Hz; (c)f=16.0 Hz; (d)f=16.0 Hz

3.1 模型

如图5所示，在背景电阻率为100 Ω·m的地下介质中存在一个长200 m厚100 m的异常体，其顶部埋深为160 m，其中ρ0=10 Ω·m，m=0.5，c=0.5，τ=30 s。采用的装置为偶极-偶极，沿x方向水平放置电偶极子，xz方向网格剖分为121×64。以下正演并行程序均在18个节点的集群上运算，其计算环境均为：Linux操作系统，CPU-Intel(R) Xeon(R) CPU E5-2620 v2 @ 2.1GHz，内存128G，开发语言为Fortran，编译器为ifort，并行环境为MPICH2。

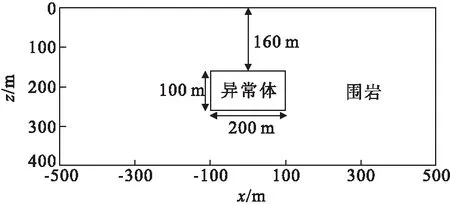
图5 低阻高级化模型Fig.5 Low resistivity and high polarization model

各个发射源对应频率的计算是独立的，基于发射源对应的频率来进行并行计算的思路，其流程如图6所示。

3.1.1 效率分析

采用图5所示的模型，21个发射源(其位置从X= -1 000 m到X= 1 000 m之间每隔100 m一个，共21个源)，从X= -1 000 m到X= 1 000 m之间每隔50 m布置一个测点，每个排列除发射源点外共40个接收点。5个频率(f= 0.1 Hz, 1.0 Hz, 8.0 Hz, 32.0 Hz, 128.0 Hz)，用不同节点数来进行并行计算，将其计算时间和串行程序计算时间统计如表1所示。

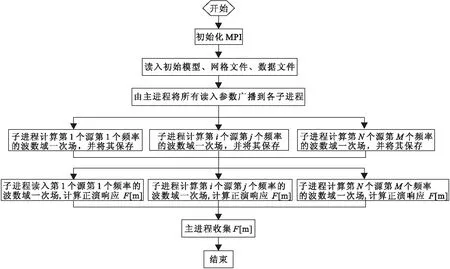
图6 正演并行流程图Fig.6 Forward parallel flow chart

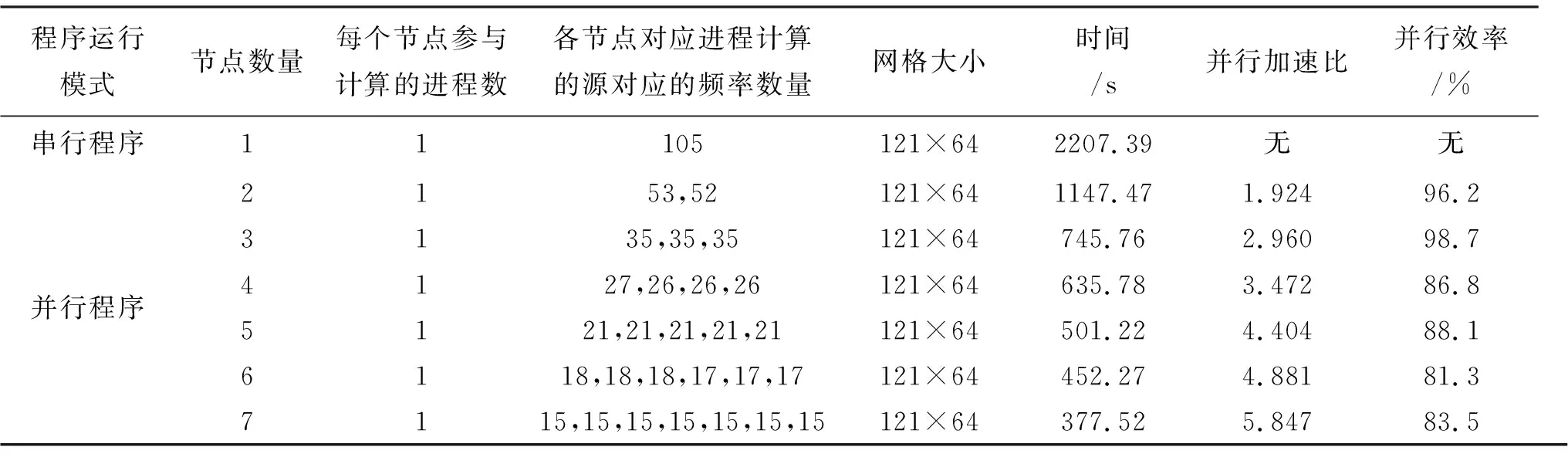
程序运行模式节点数量每个节点参与计算的进程数各节点对应进程计算的源对应的频率数量网格大小时间/s并行加速比并行效率/%串行程序11105121×642207.39无无并行程序2153,52121×641147.471.92496.23135,35,35121×64745.762.96098.74127,26,26,26121×64635.783.47286.85121,21,21,21,21121×64501.224.40488.16118,18,18,17,17,17121×64452.274.88181.37115,15,15,15,15,15,15121×64377.525.84783.5

从表1可以看出，在每个节点只有一个进程参与计算的前提下，当参与并行计算的节点数增加时，加速比增大。当有7个节点参与并行计算时，其计算速度约为串行程序计算速度的5.847倍，很大程度地降低了复电祖率法二维正演所需时间。但是，从表2中并行效率这一列看出，并不是参与并行的节点数越多，并行效率越高。当参与并行的节点数从2增加到3时，并行效率增加，而当参与并行的节点数从3增加到4(或节点数从5增加到6)时，并行效率反而降低，这是由于节点等待或节点间的数据交换等通信耗费一些时间。

3.1.2 正确性验证

采用多发射源和多频率进行正演计算时，笔者仅展示其中一部分数据的对比结果。如图7所示，图7中Tx、Rx分别代表发射源和接收点的位置，串行计算结果用红色圆圈表示，并行计算结果用蓝色点表示，计算结果完全吻合。

4 结论

当发射源、频率较多时，完成复电阻率法二维正演所需时间较长，我们通过引入MPI并行计算，实现了复电阻率法二维正演并行算法，极大地提高了正演的计算效率。通过理论模型的试算结果表明，该并行算法是可靠的，稳定的，较好地解决了复电阻率法二维数值模拟的计算速度问题，为其反演并行计算打下良好的基础。对其并行计算时间分析可知，当每个节点的进程数都为“1”时，随着节点数的增多，其并行加速比逐渐增大，但其并行效率并不与参与计算的节点数成正比。

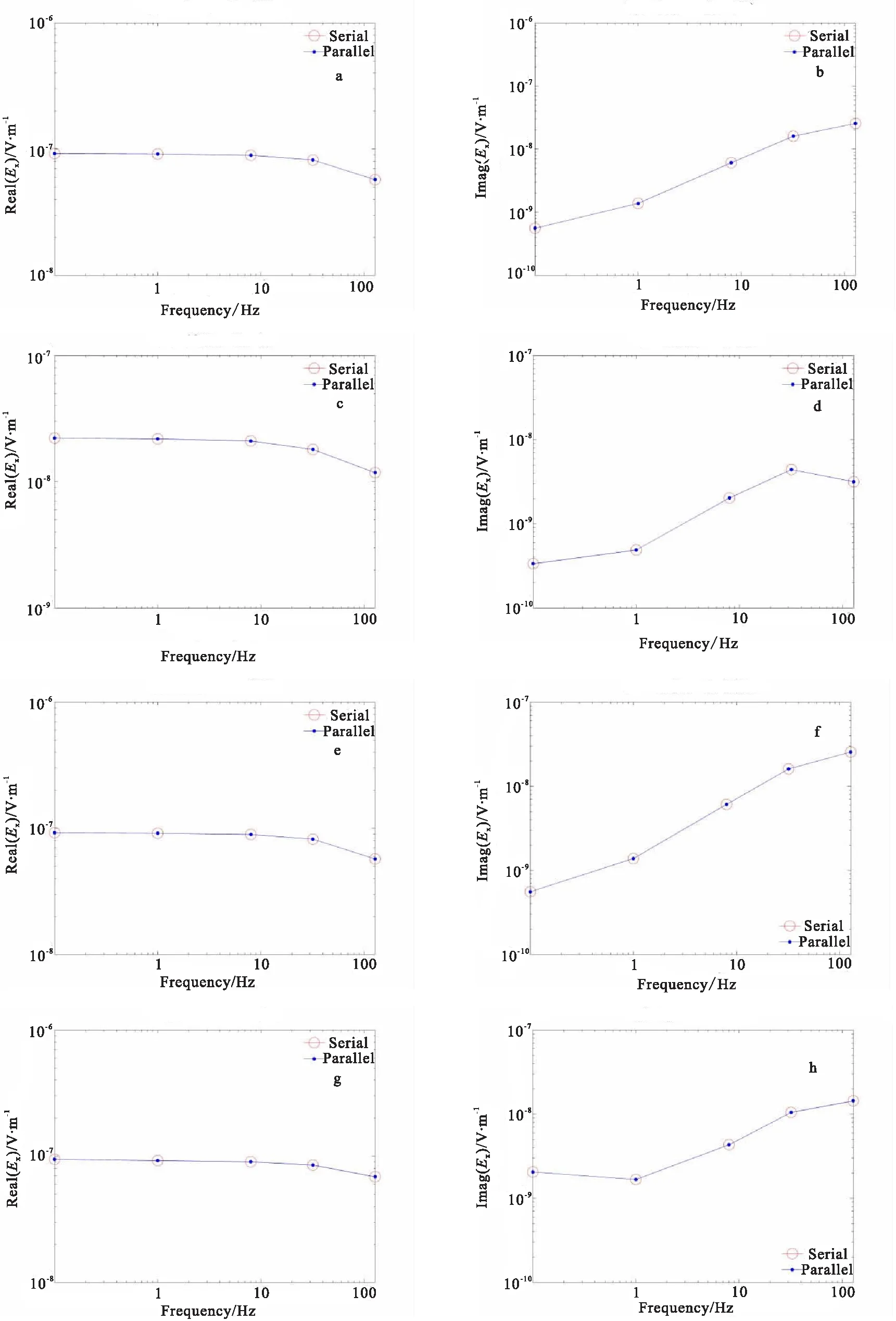
图7 正演并行结果与串行结果对比图Fig.7 The comparison between forward modeling parallel and serial results(a)Tx=-1 000 m Rx=-300 m; (b)Tx=-1 000 m Rx=-300 m;(c)Tx=-1 000 m Rx=0 m; (d)Tx=-1 000 m Rx=0 m;(e)Tx=-1 000 m Rx=300 m; (f)Tx=-1 000 m Rx=300 m;(g)Tx=-500 m Rx=100 m; (h)Tx=-500 m Rx=100 m

参考文献：

[1] 杨进. 环境与工程地球物理[M]. 北京: 地质出版社, 2011.

YANG J. Environmental and engineering geophysics[M]. Beijing: Geological Publishing House, 2011. (In Chinese)

[2] 杨振威, 严加永, 陈向斌. 频谱激电法在安徽沙溪斑岩铜矿中的应用[J]. 地球物理学进展, 2013, 28(4): 2014-2023.

YANG Z W, YAN J Y, CHEN X B. The application of spectral induced polarization in Shaxi porphyry copper in Anhui province[J]. Progress in Geophysics, 2013, 28(4): 2014-2023. (In Chinese)

[3] 曹蔚杰, 单明良, 高勇, 等. 复电阻率法(CR)在铜钼矿勘查中的应用效果[J]. 工程地球物理学报, 2014, 11(2): 203-207.

CAO W J, SHAN M L, GAO Y ，et al. The application of complex resistivity method(CR) to copper-molybdenum Mine exploration[J]. Chinese Journal of Engineering Geophysics, 2014, 11(2): 203-207. (In Chinese)

[4] 徐自生, 张丽, 唐伟, 等. 复电阻率法(CR)在内蒙古那吉河铅锌矿探测中的应用[J]. 矿产勘查, 2015(2):165-170.

XU Z S, ZHANG L, TANG W, et al. Application of complex resistivity method (CR) in prospecting lead-zinc deposit in Inner Mongolia[J]. Mineral Exploration, 2015(2): 165-170. (In Chinese)

[5] REVIl A, KARAOULIS M, JOHNSON T, et al. Review: some low-frequency electrical methods for subsurface characterization and monitor in hydrogeology[J]. Hydrogeology Journal, 2012, 20(4): 617-658.

[6] 许传建, 徐自生, 杨志成, 等. 复电阻率(CR)法探测油气藏的应用效果[J]. 石油地球物理勘探, 2004, A: 31-35.

XU C J, XU Z S, YANG Z C, et al. The application of complex resistivity method(CR) to oil gas exploration[J]. Oil Geophysical Prospecting, 2004, A: 31-35. (In Chinese)

[7]FLORES OROZCO A, KEMNA A, OBERDÖRSTER C, et al. Delineation of subsurface hydrocarbon contamination at a former hydrogenation plant using spectral induced polarization imaging[J]. Journal of Contaminant Hydrology, 2012, 136-137: 131-144.

[8] BREEDE K, KEMNA A, ESSER O, et al. Spectral induced polarization measurements on variably saturated sand-clay mixtures[J]. Near surface geophysics, 2012, 10(6):479-489.

[9] 张武生, 薛巍, 李建江, 等. MPI并行程序设计实例教程[M]. 北京: 清华大学出版社, 2009.

ZHANG W S, XUE W, LI J J, et al. Parallel programming with MPI[M]. Beijing: Tsinghua University Press, 2009. (In Chinese)

[10] 都志辉, 李三立, 陈渝, 等. 高性能计算之并行编程技术——MPI并行程序设计[M]. 北京: 清华大学出版社, 2001.

DU Z H, LI S L, CHEN Y, et al. High performance parallel computing technology——MPI parallel programming[M]. Beijing: Tsinghua University Press, 2001. (In Chinese)

[11] NABIGHIAN M. N. Electromagnetic Methods in applied geophysics[M].Theory. Society of Exploration Geophysicists, 1988.

[12] 徐世浙. 地球物理中的有限单元法[M]. 北京: 科学出版社, 1994.

XU S Z. Finite element method in geophysics[M]. Beijing: Science Press, 1994. (In Chinese)

[13] 张斌. 可控源音频大地电磁二维正反演研究[D]. 北京: 中国地质大学, 2012.

ZHANG B. Research of 2D CSAMT forward and inversion[D]. Beijing: China University of Geosciences(Beijing), 2012. (In Chinese)

[14] 张志勇. 复电阻率法二维有限元正演研究[D]. 北京: 中国地质大学, 2013.

ZHANG Z Y. 2D FEM forward modeling research of complex resistivity method[D]. Beijing: China University of Geosciences(Beijing), 2013. (In Chinese)

[15] 王寒冰. 极低频电磁法频率域二维正反演研究[D]. 北京: 中国地质大学, 2014.

WANG H B. Research of 2D frequency-domain ELF forward and inversion[D]. Beijing: China University of Geosciences, 2014. (In Chinese)

[16] 桂兵. 可控源音频大地电磁法张量数据二维反演研究[D]. 北京: 中国地质大学, 2015.

GUI B. Research of 2D CSAMT tensor data inversion[D]. Beijing: China University of Geosciences, 2015. (In Chinese)

[17] PELTON W H, WARD S H, HALLOF P G, et al. Mineral discrimination and removal of inductive coupling with multifrequency IP[J]. Geophysics, 1978, 43(3): 588-609.

[18] 林绍忠.对称逐步超松弛预处理共轭梯度法的改进迭代格式[J].数值计算与计算机应用, 1997(12):266-270.

LIN S Z. Improved iterative format of symmetric successive over relaxation-preconditioned conjugated gradient method[J]. Journal of Numerical Methods and Computer Applications, 1997(12):266-270. (In Chinese)

[19] 谭捍东. 大地电磁法三维正反演问题研究[D]. 北京: 中国地质大学, 2000.

TAN H D. A study on 3d MT forward and inversion[D]. Beijing: China University of Geosciences, 2000. (In Chinese)

[20] 胡祥云, 李焱, 杨文采, 等. 大地电磁三维数据空间反演并行算法研究[J]. 地球物理学报, 2012, 55(12): 3969-3978.

HU X Y, LI Y, YANG W C, et al. Three-dimensional magnetotelluric parallel inversion using data space method[J]. Chinese Journal of Geophysics, 2012, 55(12): 3969-3978. (In Chinese)

[21] 林昌洪. 三维大地电磁共轭梯度反演算法研究[D]. 北京: 中国地质大学, 2004.

LIN C H. A study on 3d MT non-linear conjugate gradient inversion[D]. Beijing: China University of Geosciences, 2004. (In Chinese)

Astudyonparallelcomputationfortwo-dimensionalcomplexresistivityforwardmodeling