直面生之困，再向“植树”行

丁丽

【教学实录】

一、直入课题，呈现调查

师：同学们好！在上这节课前我们完成了一个课前调查。52人中，有32人表示学过植树问题。是不是都学好了呢？后面还有两个题，我們一起来看看答题情况（如图1），你能看得懂这个结果吗？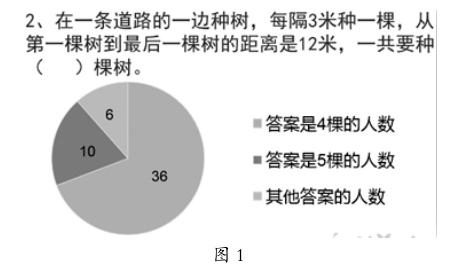

学生表述调查结果。

二、直面问题，图画确认

师：这道题的正确答案只有一个。是4、5还是其他答案呢？有没有什么办法，让大家一眼就看出哪个答案对？

生1：请这几个学生分别说道理，再看谁的对。

生2：我觉得说道理不好，谁的道理对还是要老师才能评判。我们可以画个图看看谁的对。（其他同学觉得画图好）

师：为了保证做对，我也画了图。每隔3米种一棵，我就3米3米地画：3米、6米、9米，够长了吗？（生：不够，还要加一段3米的）好的，接下来就该画树了。树应该种哪里？伸出你的手指，边指边数是几棵树。（学生数，课件动态演示，如图2）答案是多少？（生：5棵）能确认吗？（生：能）确实，图一画，结果一目了然！再回头看答题情况：我们班52位同学只有10位做对了。看来，学过不一定学好了！其实，丁老师之前还找了三个不同年级的孩子也做了这道题，发现学过植树问题的同学出错不少。我在想，做数学题，我们到底追求什么？

生3：要能做对就好！

师：那有没有什么办法可以保证做对？

生4：画个图，确认一下。

师：那好，这节课，我们就约定：做题都请画图确认一下，让它想错都难，好不好？

三、学习画图，讨论梳理

师：这样的图，你会画吗？画的时候要注意什么？

生5：我觉得图还可以简单点，直接画线段，不要画那么漂亮的树。

生6：要看清楚条件，不能把条件画错了。

师：感谢你们的宝贵建议。不过，植树问题很多时候都是不种树的！接下来，请独立解决这样的题，别忘了，要保证对！（分发学习单，如下）

学生独立完成，教师在巡视的过程中，鼓励先完成的学生向同桌介绍确认的过程。

师：绝大部分同学都独立完成了2道题，并分享了自己的确认过程。这是两名同学的思考。请先看第一幅图（如图3），你觉得对不对？你是怎么确认的？

生7：我觉得他画对了，因为我的和他的一样。

师：你们两个画法一样，所以你认为对。如果你和他的画得不相同，他的就一定错了吗？

生8：我觉得要看条件画对了没有。题目说8米，我们就数一下是不是8米。每2米切一段，一开始和最后都不要切，图中的那个长竖线就是切的地方，所以是3次。

师：你是善于分析的孩子！下面，我们带着这种分析的思路一起确认第二幅图。（如图4）你有什么问题要问作者的吗？

生9：我不知道那个24除以6是什么意思。

生10：我是想看看24米里面有几个6米，就把圆分成了4份。

生9：我现在懂了。不过你为什么还要画图？

生10：因为我不知道4个6米是不是4盆花。

生9：我现在都懂了，没问题了。

师：谁来确认？

生11：我数了，是有4个6米，也就是24米。然后每2盆兰花都隔了6米，2盆兰花之间还都有1盆杜鹃，我认为是对的。

生12：我觉得加个说明就更好了。比如粗线是什么，细线是什么，也方便检查。

师：都是善于观察和思考的孩子！图画好了，答案也出来了，你们是否画了图？都对了吗？（了解、调整个别学生的图的问题）看来，图画对的孩子都非常漂亮地解决了植树问题中很难的问题。刚才巡查中，我发现有同学直接画出结果，有同学先写出算法，再画图确认，这两种方式都值得表扬。用这种研究问题的态度和方法去面对问题，我们将屡战屡胜！不信，请看！（出示题目如下）

三、研究问题，内化提升

师：大家先独立研究，有想法了请举手示意。

学生独立研究，教师巡视，请一名学生带作品上台展示（如图5）。

师：大家看得懂吗？你有什么问题要问他？

生13：请问21是什么？

生14：我这里画了21盏灯。（用手指向图中的小竖线）

生13：2又是什么？

生14：我觉得画2000米太麻烦，我就画了1000米，1000米里面有21棵，所以2000米会有2个21棵，所以乘2。

生13：我听懂了，没问题了。

师（问生13）：你觉得对吗？

生13：她说的很有道理，我觉得对。

师：有办法能确认吗？

生13：那就要全部画出来才行。

师：你若愿意花时间，全部画出来也没什么难的，只是细致点，别画错、数错就好。既然生14说她觉得麻烦所以才画一半，那如果是这样，我还画少点岂不是更方便？（生：可以）你们说画多少？（生：画200米）

生15上台画图，如图6。

师：我突然发现一个问题，如果2000米只画1000米再乘2是对的，那么只画200米再乘10也应该对！大家看看，是一样的结果吗？

师：谁能听懂？能不能举例说明这个说法是否合理？

生20：他的意思是5比4多1，21比20多1，如果不看这么多段，也是这样。比如只看3段，有4盏灯。

师：如果是这样，那么这个题该是多少盏灯？生21：41盏，因为2000除以50还要加1。

师：正如大家所说，这样的方式证实了41是正确答案。刚才这道题，两位同学都画了图，这个问题的图和之前的三幅图一样吗？不一样在哪里？这样的研究方法妙在哪里？

生22：这里的图不一样，之前都是画出多少就是多少，现在没画那么多，我们也知道是多少了。

师：你的意思是不是可以理解为———之前我们是直接画出结果，这里的图是帮助我们研究题目特点的？（生22：是的）有了这样的研究之后，不论路有多长，都可以解决了。图还是要画，我们可以通过画图研究问题。我留了2道挑战题，供你们课后研究，有信心解决吗？（出示题目，如下）

四、总结分析，渗透解决问题的策略

师：时光匆匆，这节课即将结束，你能否对自己或即将学习这个内容的同学说点什么？

生23：做题要细心点，有想法了还不能忘了要确认。

生24：画图解决问题是个好办法。

生25：不要背那么多公式也是可以解决问题的。

师：同学们总结得很好。今天，我们从一个前测题的分析开始对植树问题这一类题进行了研究，找到了保证做对的重要手段———画图。掌握了画图的方法，一定能帮你们解决更多的问题！

【研磨思考】

2008年，我执教的“植树问题”获得长沙市小学数学课堂教学竞赛一等奖。为了上好这节课，我们当时在3所学校选取了三、四、五年级各两个班学生进行了学情调查，前测题第一题为：将12米的路，每3米分一段，可以分成几段？学生的答案让我惊讶：明明就是一个求12里面有几个3的问题，不少学生用12除以3的结果4加1或者减1。通过进一步访谈发现，这些加1或减1的学生都提前在课外学过植树问题。当问及为何要加1、减1时，学生的回答再次让我惊讶：以前学植树问题时有3个公式，這道题里没说是哪种种法，不知道该怎么办，所以选择加1或减1。调查到这里，我明白了，这些学生都是按3种种树情况学了公式的，并且看到“路”“段”就开始模式辨认，套用公式解决问题。这显然不应该是一个有数学素养的学生应该具备的解题方式，也不应该让学生用生搬硬套地方式来学习数学。于是，在当年的教学实践中，我带领学生通过实验探究，理解植树问题中棵数与段数的关系并探寻出三种算法后，将黑板上的三种算法一擦，提出问题：“数学公式这么多，要记牢还挺不容易。若是真忘了，你有办法把它找回来吗？”此问以期引导学生用画图、验证、找事实、寻求规律等方法面对一个问题、研究一个问题，而不是简单识别所谓的模式再套用。如果用套模式这样的方式学习，得到的结果不仅易错（题目变化万千，稍有调整学生便会束手无策），也会让学生对数学学习产生误解———多背公式就能学好数学。

时隔10年，直面生之困，再向“植树”行。此次的设计有了更朴素的做法———从一题到一类，再到一法，全课只字不提算法，更不用说进行分类讨论、逐一辨识。此次的设计是希望能进一步破而后立，真正解决学生学习中的问题。我在备课研磨中，学习了很多老师对这一内容的解读，以及教学处理方式，发现他们基本上都是分三类情况讨论，大多都总结了算法。那么，随之而来我要思考并理顺以下的问题。

1.植树问题的教学中存在什么问题？

从这十年间听过、磨过的植树问题教学来看，学生学得并不好，至少不如我们所期待的好。多次调研数据显示，学生参与课外学习的人数与日俱增，而学习的方法更多的是先学习公式再辨认模式，学习的结果就变成了“一看以为会，一做竟然错”，让学生大呼难学，教师大呼难教。教材分别呈现了“两端都种”（教材例题上写明了这个要求）、“两端不能种”和封闭图形上的种树三道例题，于是一般的处理方式就变成了要么一节课突破一种算法，最后再比较异同，区别计算；要么一节课教三种算法，再模式辨认，而后是变式练习。这两种教法都直指快速得到答案。对于给定一种算法，再直接套用自然比通过研究得到答案来得快，但这不应成为教学的追求。数学学习讲究通法为先———越是简单、朴素、适用性广的方法，越容易被理解、应用和学习。画图显然满足这一特点。那么画什么、怎么知道画对了就成为用这一方法解决问题的关键。一旦引起学生的关注，他们要掌握并不难。在我看来，教材只是提供了教学的素材，处理教材的原则就在于处理好“这是什么“”为什么教”和“教什么”三者的关系。植树问题大可不必分情况讨论，没有“两端都种”，如果觉得表述不清楚，“从第一棵到最后一棵间隔多少米”就是一种非常明确的表达方式。至于突然出现了一座房子一端不能种树了、出现2座房子或者别的障碍物所以两端都不能种了，不用区别对待，把不种的那几棵拿走就行了，总不至于中间还有几棵也不种了所以还要另起炉灶重新研究算法。学生学起来难，教师教起来效果不好，恰好说明教师把内容“咬得太碎”教给孩子，失去了原本应有的营养，导致学生学起来索然无味，如同嚼蜡。

2.学完植树问题后，学生应当收获什么？

作为数学广角的学习材料，不同于基础知识和基本技能，它更多地是在积累经验、习得方法和应用数学的过程中形成解决问题的能力。这种能力是数学教学必须着重培养的数学素养之一。那么，学生学完植树问题后，敢于面对一个问题、会研究一个问题及能对一个问题的结果负责就是我对这节课的学习价值定位。这三个方面对应的分别是信心、方法和态度。用什么树立信心？大量的正确解答的体验让学生感受到哪怕是不一样的题，也是可以被解决的。用什么来保障这种信心的确立？通过画图与分析的手段，能正确解答植树问题———想直接画的，可以把结果画出来，愿意只画一部分图的，可以为自己寻求解答方法提供依据。得到了一个结果怎么办？用画图、举例的方法确认自己的答案，而非只是认为自己的答案不会错，从而让验证所得到的解与教材上的回顾与反思不至于形同虚设。这样的目标落地之后，培养学生借助图形解决问题的意识和针对不同问题的特点灵活解决问题的能力，以及积累数学基本活动经验，树立能解决好数学问题的信心等就不再是镜中花，只可观而不可及了。

（作者单位：长沙市中小学教师发展中心）