引入条件异方差效应的CAPM模型簇改进

(安徽工业大学商学院，安徽马鞍山243032)

CAPM(capital asset pricing model)模型又称资本资产定价模型，由Sharpe[1]、Lintner[2]和Mossin[3]在马 科维茨投资组合理论基础上发展而来。它是一种关于定价和度量风险和收益的均衡理论，其计量模型表示如下。

其中：Rt、Rf、Rmt分别表示时刻t证券、无风险资产和市场收益率；εt为随机扰动项；β1为市场风险因子，理论上要求β1＞0；α为截距项,理论要求为零。该模型表明当市场达到均衡时，资产预期回报率与市场风险系数 β1相关。Jensen等[4]和何惠珍[5]检验了CAPM模型的有效性，结果表明 β1＞0，但邹舟等[6]和赵雪莹[7]的研究却没有支持CAPM模型。这表明该模型仍然存在一定局限性，主要体现在三个方面：现实条件很难满足CAPM模型的假设前提；市场风险系数β1值难以精准确定；市场风险很难完全解释股票收益率。为此学者们开始关注系统性风险以外的其它因素。Fama等[8]结合Banz[9]和Rosenberg等[10]研究结果建立如下三因子模型，该模型计量表示形式如下。

其中RSMB、RHML分别为市值风险和账面市值比风险。陆旖蔚等[11]基于三因素理论，研究中国股市的溢价问题，结果显示我国股市呈现价值溢价与规模溢价并存现象。王珺等[12]、Aggarwal[13]分别对中国股市和印度股市进行研究，结果均表明三因素模型的解释力度强于CAPM模型。随后Aharoni等[14]又证明了上市公司的盈利因子和投资因子与超额收益率之间也存在相关关系，为此构建了包含盈利因子和投资因子的q因子模型，并运用该模型对美国股市进行了研究，显示该模型的优越性。Fama等[15]在意识到三因素模型不足后，于2015年提出五因素模型，即在三因素模型基础上添加了盈利能力因子(RMW)和投资模式因子(CMA),该模型的计量表达式为

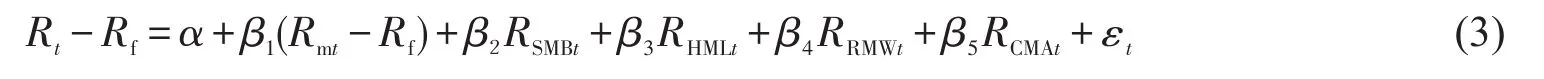
Fama等[16]的研究结果显示五因素模型的解释能力更强，但邹羽[17]将五因子定价模型应用到我国股市实证分析时，发现市场因子是影响股票收益最显著因子，随着规模的变大，规模因子对超额收益率的影响会消失。赵胜民等[18]选取我国股市1995—2014年的股票月度数据，对三因素模型和五因素模型进行对比分析，研究结果显示，三因素模型在我国市场上的适应性更强，盈利因子和投资因子对投资组合的收益率影响不显著。

以上三个模型有2个共同特点：三个模型均使用经典假设的OLS估计，认为模型中的扰动项εt为同方差。Bao等[19]对此进行改进，将扰动项设置为非对称的幂函数形式，该分布随参数的变化而出现左偏和右偏两种形式，且需要用极大似然估计方法，但本质上仍属于同方差范畴；三个模型中均没有考虑到波动率风险因子。理论研究认为，金融时间序列的收益率波动具有明显的集群性和条件异方差性，因此使用同方差假设的扰动项不符合实际数据分布要求。另外CAPM模型本身基于马科维茨投资组合理论演化而来，但没有将收益率的波动率作为风险因素引入到模型中。有鉴于此，本文试图对这三个模型进行改进，引入条件异方差模型刻画扰动项εt，并将异方差作为风险因子并入模型，构造出新的多因素模型。

1 异方差引入与模型改进

1.1 条件异方差模型与扰动项分布改进

广义条件异方差模型又称为GARCH模型，由Bollerslev[20]在Engle[21]的自回归条件异方差(ARCH)模型基础上进一步扩展而来，GARCH(p,q)模型形式如下：

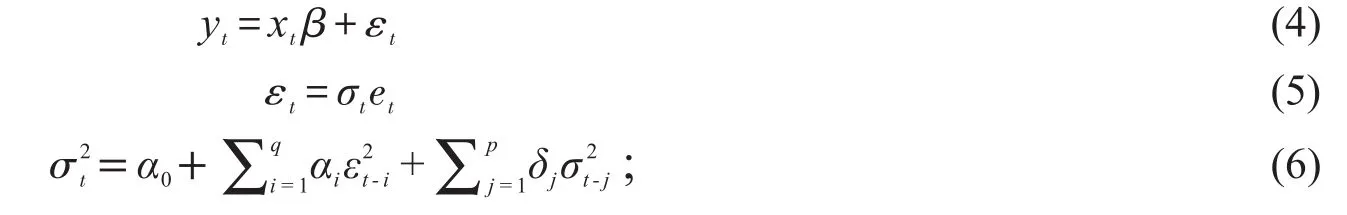
其中：σt为扰动的标准差；et是均值为0方差为1的独立同分布随机变量序列，通常假设服从标准正态分布。模型的平稳性要求系数满足如下条件：

为改进经典CAPM模型簇，文中首先要检验上述三个模型的扰动项是否存在异方差，这可以通过使用拉格朗日乘子LM检验，原假设为不存在ARCH效应，备择假设表示存在ARCH效应，在原假设成立时，LM检验量服从卡方分布。关于该检验量的构造可参见文献[22]。在检验存在异方差的基础上，在模型(1)～(3)中引入条件异方差效应，使用极大似然估计的方法替代经典OLS方法估计上述3个模型。

1.2 风险因素引入与模型改进

金融理论认为，收益率的波动率可以作为资产风险度量，同时也是影响资产收益率的重要因素之一。在经典CAPM模型簇中，由于假设扰动项为同方差，因此无法将方差作为风险因素引入到模型中，而经过扰动项改进后，可以将异方差σt作为风险因子引入到上述3个模型中进行拓展，如就模型(3)而言，引入风险因素的计量模型记为

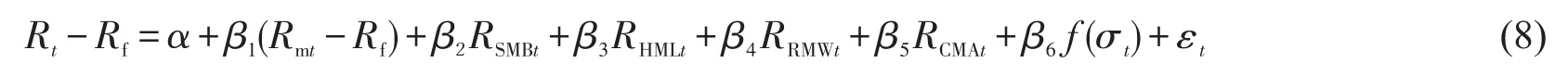
其中εt～GARCH(p,q)。f(σt)常见形式有如下3种

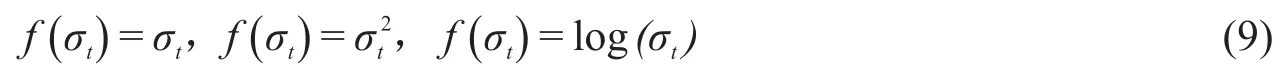
记上述引入条件异方差效应后的模型仍为模型(1)～(3)。接下来的分析将首先检验各个模型扰动项是否存在条件异方差效应，然后引入风险因子改进现有三个模型。

2 CAPM模型簇的实证研究

2.1 描述性分析与相关性分析

为考察CAPM模型与改进模型的合理性，本文使用美国产业月度数据进行实证研究，以银行业为检验对象，样本期限为1963年7月至2018年2月，共656个观测来源于文献[23]。根据模型(1)至模型(3)中变量定义，记RBANK_RF、RMKT_RF分别为银行业收益率和市场收益率扣除无风险收益率后的超额收益率指标，即有

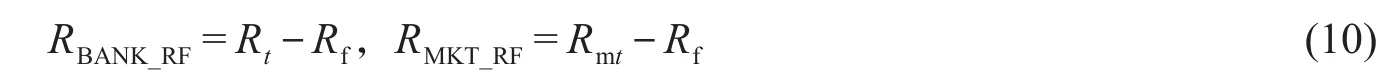
其它指标采用上述模型中因素的记号。首先给出分析变量的常见描述性统计量如表1。表1中，银行业超额收益率RBANK_RF的均值为0.862%，中位数为1.080%，故均值略小于中位数，从而分布为负偏，这从其偏度为-0.405得到验证。指标的最大值和最小值分别为21.920%和-21.130%，两者相差较大，说明在所考察的时间段内，银行业收益率变化幅度较大。该指标的峰度为6.104，明显大于正态分布对应的峰度3，因此该指标明显具有负偏尖峰特性，具备金融资产收益率波动的一般特征。基于正态分布的JB检验量值高达210.942，对应的检验概率近似为0，因此拒绝原假设，表明该指标不服从正态分布。图1为该指标的时序图，图1表明收益率波动存在明显的集群和异方差性。对其它变量也可以类似进行分析。

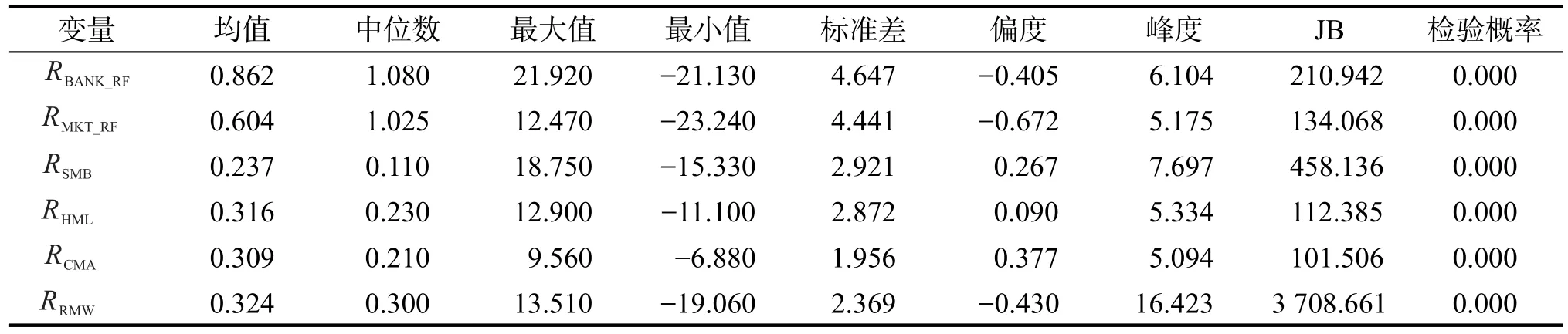
表1 变量描述性分析Tab.1_ Descriptive analysis for variables

表2给出了分析指标之间的相关系数及其显著性检验结果，其中“***”表示相关系数在0.01的显著性水平下通过显著性检验，表明相关系数显著非零。表2表明，变量RBANK_RF与5个因素的相关程度分为3类：与RMKT_RF、RSMB和RHML的相关系数，取值分别为0.707、0.396和0.151，都为正相关，且高度显著；与RRMB的相关系数，取值为-0.191，也高度相关，但为负相关；与RCMA的相关系数，取值为-0.072，没有通过显著性检验。相关性分析表明，对银行业超额收益率而言，市场因子具有最大的正向影响，而RRMB为反向影响，RCMA的影响不显著。

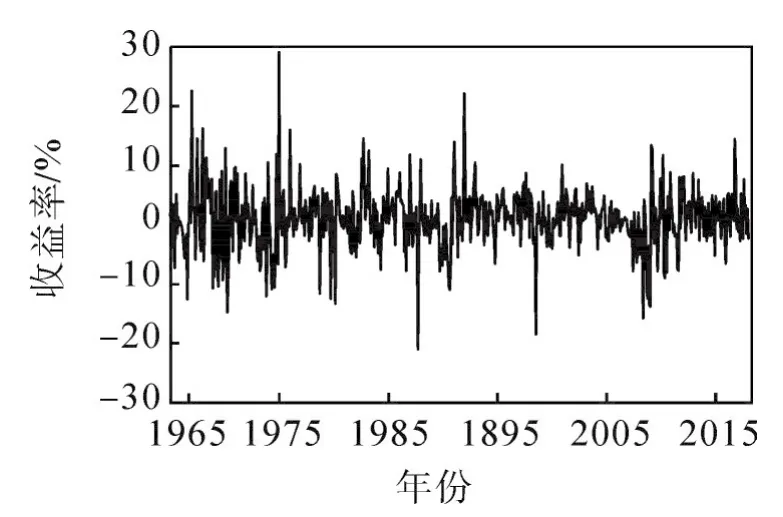
图1 变量RBANK_RF的时序图Fig.1 Timing diagram of variableRBANK_RF

2.2 单位根检验

考虑到使用时间序列变量进行回归分析，为防止伪回归，应检验各个变量是否存在单位根，本文采用ADF单位根检验，并使用AIC指标选择合适的滞后期。由于表1中各个变量的均值与0有一定的差异，故选择含有常数项检验模式，结果如表3所示。由表3可以看出，变量RBANK_RF的ADF检验值为-5.895,1%、5%和10%显著性水平下的临界值分别为-3.440、-2.866和-2.569，有检验值小于三种检水平下的临界值，因此拒绝存在单位根的原假设，表明该序列为平稳过程。类似地，剩下的各个变量ADF检验值也均小于三个显著性水平下对应的临界值，因此都拒绝原假设，各变量都不存在单位根，因此本文考察的单因素模型、三因素模型和五因素模型均不会产生伪回归现象。

表2 变量相关性分析Tab.2 Correlation analysis for variables

表3 变量单位根ADF检验Tab.3 Unit root tests for variables

2.3 经典回归分析

分别使用OLS方法估计单因素、三因素和五因素CAPM模型，结果见表4所示。下文以“***”、“**”、“*”分别表示估计量在1%、5%和10%显著性水平下通过检验，即系数非零，从而对应因素对银行业超额收益率有显著影响。表4表明，在单因素模型(1)中，市场超额收益率RBANK_RF的系数估计为0.838，在0.01的显著性水平通过显著性检验，且显著大于零，这符合经典CAPM模型要求。类似地，在三因素模型中，因素RMKT_RF的系数估计为0.845，因素RSMB和RHML的系数估计分别为0.510和0.621，三个估计值均在0.01的显著性水平通过显著性检验，这说明银行业超额收益率与RMKT_RF、RSMB和RHML呈现正向关系。在五因素模型中，市场因素RMKT_RF、RSMB和RHML的系数估计分别为0.843、0.554和0.688，都在0.01的显著性水平通过显著性检验，而且都是正相关。而因素RCMA的系数估计为-0.153，即使在0.10的显著性水平下也没通过检验，说明该因素对银行业获得超额收益率没有影响。因素RRMW的系数估计为-0.185，在0.05的显著性水平下有通过检验，说明该因素对银行业获得超额收益率有抑制效应。从表4还可以看出，扰动项的Breusch-Godfrey检验(滞后期为2)表明存在自相关，因此估计量都使用稳健性方差估计。扰动项ARCH效应(设置滞后期为5)LM检验结果显示三个模型扰动项在0.01的显著性水平下均拒绝为同方差的假定，表明三个模型存在异方差，因此需要进一步对扰动项方差进行估计。

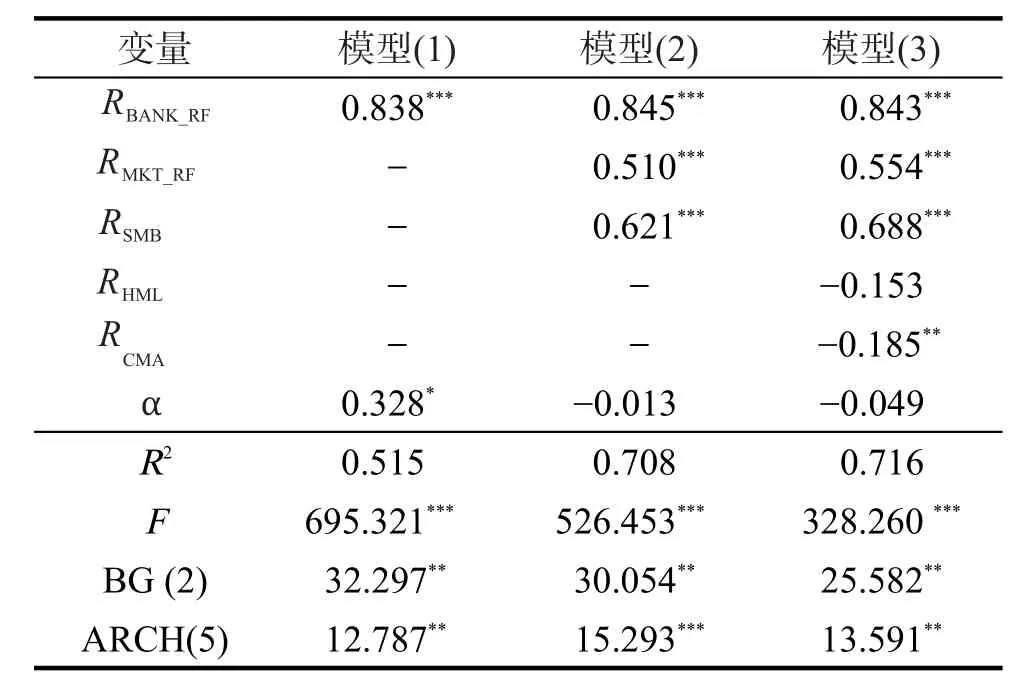
表4 经典模型的OLS估计与检验Tab.4 OLS estimation and test for classical models

2.4 改进后模型分析

通过比较 GARCH(1,1)、GARCH(1,2)、GARCH(2,1)、GARCH(2,2)模型对应的信息指标以及估计参数的显著性，发现使用GARCH(1,1)模型刻画扰动项的条件异方差性最为合适，同时也没有检验到存在非对称效应，因此最终选择GARCH(1,1)模型，结果如表5所示。表5表明，考虑条件异方差效应后，模型(1)、模型(2)各个因素的显著性与参数估计大小没有发生实质性变化，但模型(3)中因素RCMA估计值在0.05的显著性水平下显著为负，且因素RRMW的系数估计发生了变化。GARCH(1,1)模型中三个参数均至少在0.10的显著性水平下通过显著性检验，表明有必要对扰动项估计GARCH(1,1)模型。引入GARCH（1，1）模型后扰动项的条件异方差效应LM检验结果显示，三个模型的检验量值分别为3.196、2.733和2.698，此时即使在0.10的显著性水平下也不能通过显著性检验，说明GARCH(1,1)模型已经充分提取异方差信息，引入条件异方差效应的改进模型比较合适。

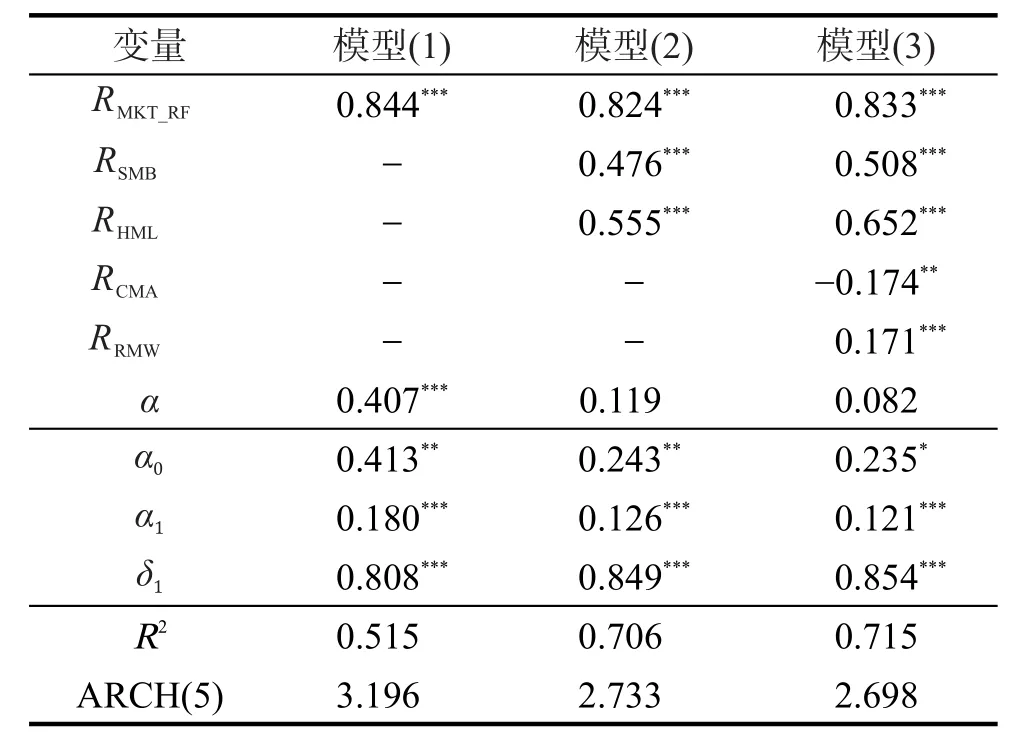
表5 GARCH效应经典模型估计与检验Tab.5 Estimation and test for classical models with GARCH effects

针对第一种模型，将波动率作为风险因素引入到三个模型中，参照资产组合理论，使用f(σt)=σt作为风险度量指标，估计结果如表6所示。表6显示，当同时使用GARCH模型刻画扰动项波动规律，且将扰动项波动率作为风险因素引入到三个模型时，与表5相比，各经典因素对应估计量的显著性与符号没有发生实质性变化，标识异方差效应的GARCH(1,1)模型三个参数α0、α1和δ1显著性和符号也没有发生明显变化。标识风险因素σt在三个模型中的估计值分别为0.243、0.112和0.140，分别在0.05、0.10和0.10的显著性水平下通过显著性检验，且均为正，这表明银行业的超额收益率与其承担的风险为正相关关系，即风险得到超额收益率的补偿，这符合经典投资理论要求。表6还表明，此时三个模型的条件异方差效应检验值为2.575、2.651和2.522，也在0.10的显著性水平下接受原假设，说明此时模型不再含有异方差性，再次表明GARCH(1,1)模型的合理性。总体来说，表6的检验结果验证了文中模型改进的合理性和必要性。

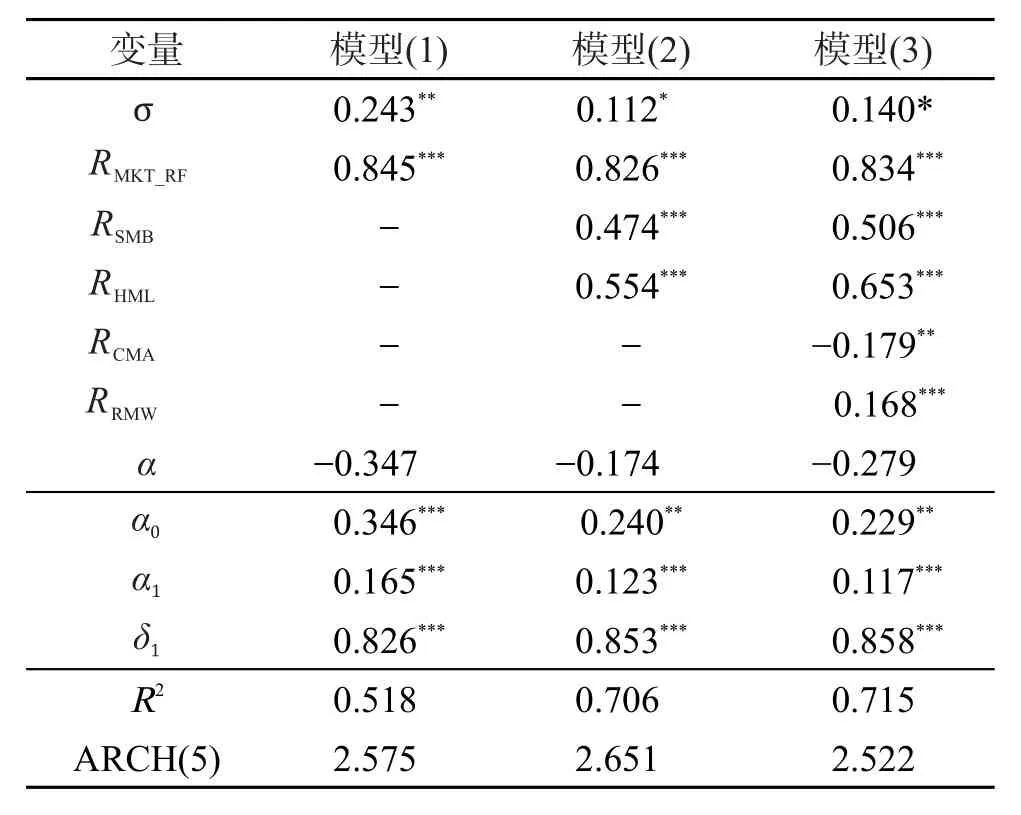
表6 风险因素和GARCH效应估计与检验Tab.6 Estimation and test with risk factor and GARCH effects

3 结 论

针对经典CAPM模型及其扩展模型的不足提出两点改进，并使用实际数据进行实证检验，得到以下几点结论。

1)经典CAPM模型簇虽能检验出影响银行业超额收益率的主要因素，但存在明显的不足，首先表现为模型扰动项不满足同方差假设；其次是对个别因素不能有效识别，如投资模式因子RCMA就属于此种情况。

2)当引入GARCH(1,1)模型刻画条件异方差后，不但能够充分提取扰动项的波动规律，还能发现影响超额收益率的潜在因素。

3)当将波动率作为风险因素引入到CAPM模型簇后，检验表明风险因素的确能够影响超额收益率，且满足风险补偿机制要求。