基于角焊缝缺口系数数据库建立及应用

施斌

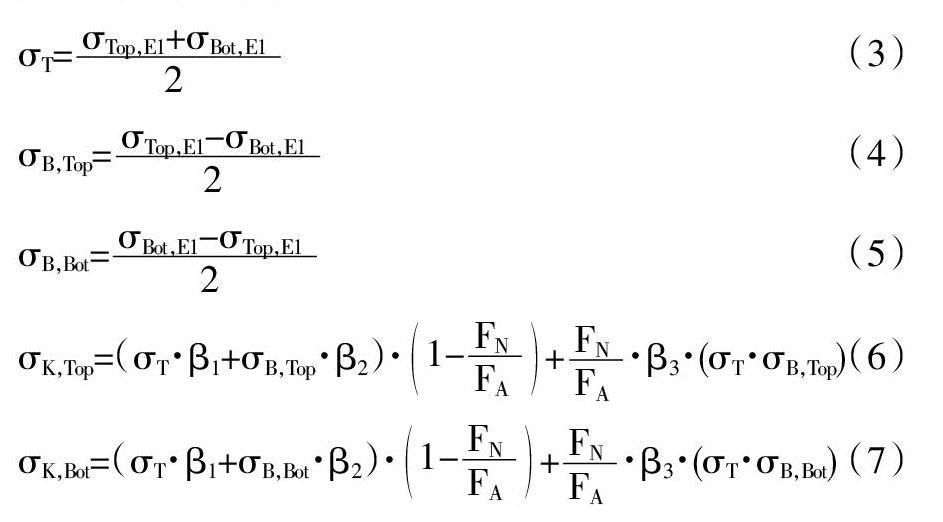
摘 要：文章结合Neuber提出的虚拟缺口半径理论，利用Radaj焊接结构的缺口应力疲劳分析方法，针对某公司30%焊透率的T型焊缝建立了满足自身要求的焊缝缺口应力集中系数数据库。通过路试采集的道路谱进行整车多体动力学载荷分解，得到焊缝疲劳分析的拖曳臂硬点载荷输入，并结合疲劳分析软件Femfat为焊缝的评估提供了一套有效的分析方法。结果表明，新建的焊缝数据库有效的预测了焊缝失效，并在路试中得到了验证，为项目开发的前期产品改进提供理论依据，能够有效节约开发成本，缩短开发周期。

关键词：角焊缝；缺口应力集中系数；疲劳损伤；有限元分析

中图分类号：U462.1 文献标志码：A 文章编号：2095-2945（2018）19-0001-05

Abstract： Based on the virtual notch radius theory proposed by Neuber and using the notch stress fatigue analysis method of Radaj welding structure， a database of notch stress concentration factor of a certain company with 30% penetration rate is established. According to the road spectrum collected by road test， the multi-body dynamic load decomposition of the whole vehicle is carried out， and the hard-point load input of the towed arm of weld fatigue analysis is obtained. Using the fatigue analysis software Femfat， a set of effective analysis method is provided for the weld seam evaluation. The results show that the new weld database can effectively predict the weld failure and be verified in the road test. It can provide the theoretical basis for the early product improvement of the project development， effectively save the development cost and shorten the development period.

Keywords： fillet weld； notch stress concentration factor； fatigue damage； finite element analysis

1 概述

焊缝的焊趾焊根处的缺口容易出现局部应力集中，这是造成焊缝开裂的一个重要原因，如果能准确预测焊缝的疲劳性能将会对结构强度设计有着重要的指导意义。焊趾焊根的缺口应力集中系数是焊缝疲劳分析的关键参数，较为真实的反映了焊缝缺口处的应力状态。由于焊缝结构多样及载荷的复杂性，用试验的方式得到焊缝缺口系数难度较大，采用有限元方法建立针对自身焊透率的焊缝缺口应力模型是得到焊缝缺口系数的较为理想的方法。

FEMFAT是一款成熟的疲劳分析软件，集成了Neuber及Radaj的焊缝缺口分析理论[1]，本文针对某公司自身30%焊透率的T型焊缝标准，对FEMFAT焊缝缺口数据库进行了扩展， 并针对某款车型路试中采集的道路信号进行多体动力学虚拟迭代，得到各硬点载荷并进行悬架疲劳分析，有效解决了拖曳臂的焊缝开裂问题[2-4]。

2 T型焊缝特征

图1为T型焊缝断面示意图，T型焊缝属于典型的角焊缝类型，即沿两直交零件的交线焊接，焊接接头由焊缝金属、热影响区和母材组成。焊缝表面与母材的交界处为焊趾区域，焊缝背面与母材的交界处为焊根区域。t1，t2为母材厚度，d为熔深，焊透率η为焊件的焊透程度，以熔深与母材厚度的百分比表示。本文采用某公司底盘零部件30%焊透率的T型焊缝，即d与t2的比值为30%。

在外部载荷作用下，接头表面的应力分布有所差异，图2为T型焊缝应力分布示意图，远离焊缝的名义应力区域受焊缝缺口的影响较小，越是靠近焊接接头应力越大，焊趾焊根处的缺口应力集中效应最为明显，其较高的缺口应力是焊缝失效的主要原因。

焊缝的开裂主要是由垂直于焊缝方向的正应力σ⊥引起的，该正应力通常来源于焊缝周围钣金件所承受的拉伸（F）及弯曲（M）载荷，切应力στ对焊缝开裂的贡献量较小。

3 T型焊缝数据库的建立

3.1 焊缝缺口尺寸的确定

焊缝缺口应力集中系数是确定缺口真实应力的关键，由于焊缝形式多种多样且结构参数复杂，直接获得缺口应力集中系数难度较大，通过有限元方法建立参数化的焊缝模型是解决这一问题的有效方法。

如何定义焊缝缺口的尺寸，如图3所示，Neuber提出了一个简单有效的方法：焊趾和焊根可以看作是不同角度（如135°和0°）的V形缺口，焊缝的缺口应力分析可以建立在V形缺口应力场基础上，缺口角度α和缺口半径ρ具有任意性[5-6]。

3.2 缺口应力集中系数

对于动态载荷下低承载能力的焊缝来讲，焊缝缺口处的应力评估非常重要。Radaj法是确定焊缝缺口影响的一种常用方法[7]，通过有限元计算得到不同焊缝类型焊根、焊趾處的应力集中系数，为进一步计算焊缝疲劳提供理论依据。FEMFAT焊缝数据库中没有焊透率为30%的T型焊缺口参数，本文意在通过Radaj法得到30%T型焊缺口参数，用于焊缝疲劳强度的预测。

垂直于焊缝方向的正应力对焊缝的影响较大，为了得到这种应力状态下的焊缝应力集中系数，对焊缝截面进行网格细化，采用平面应力单元（默认单元厚度为1mm），焊根、焊趾处的半径ρf为1m，钣金厚度为10mm。有限元求解器采用ABAQUS。考虑到焊缝在实际过程中受到拉压、弯曲等影响，对焊缝模型确定了三种加载方式，如图4中的拉伸载荷1、弯曲载荷2、拉伸或弯曲载荷3（3'），载荷3（3'）是考虑焊接件载荷传递的影响。各载荷大小根据焊接件的截面尺寸而定，目的是使焊缝名义应力区域为1Mpa，这样焊根、焊趾处的最大应力可以作为应力集中系数保存在焊缝数据库中。

根据材料力学梁的拉伸（1）及弯曲（2）正应力计算公式可以反推出载荷大小，如图5所示。则拉力F为10N，弯矩M为16.67N.mm。

σF=F/（b*h）=1Mpa （1）

σM=M/（b*h2/6）=1Mpa （2）

当拉伸、弯曲载荷大小确定后，需要考虑尽可能多的约束加载方式，并从中选取最终形式，选取原则为使得当前约束加载方式下对应的焊趾、焊根缺口系数最大[8-9]。

如图6所示，Toe為焊趾，Root为焊根，E1，E2，E3为焊趾焊根处的三个评估单元，新建焊缝数据库中包含了以下缺口系数：Toe（E1），Toe（E3），Root（E2，E3）。E1用于评估焊趾Toe（E1），E2用于评估焊根Root（E2），E3用于评估焊趾Toe（E3）及焊根Root（E3）。为了得到上述参数，对细化的焊缝模型进行计算，选取较为保守的四种约束加载方式（所求缺口系数最大），如图7所示。图8为应力结果云图。记录各焊趾焊根的缺口系数β1、β2、β3，如表1所示，并扩展到Femfat焊缝数据库中。

3.3 真实缺口应力

在动态载荷作用下，焊接部件的承载能力明显降低，因此焊缝区域的应力评估非常重要。许多标准提供了焊缝的评估方法，这些方法是根据焊缝类型和应力，给焊接接头分配评估级别。本文采用BS 7608标准对焊缝进行评估[10]。

得到焊根、焊趾缺口系数后，可以计算结构在时域信号下任意时刻的焊缝真实缺口应力。以焊趾Toe（E1）为例，如图8所示，名义应力区域评估单元E1在任意时刻下垂直于焊缝方向的正应力可以由拉伸及弯曲载荷下的两个正应力分量组成（？滓T为拉伸正应力，？滓B，Top及？滓B，Bot为钣金上下表面的弯曲正应力）。

4 工程运用

本文中的车型针对强化路试规范，采集了试验场路面信息，并通过多体动力学虚拟迭代，分解出用于疲劳分析的相关硬点载荷[11]。

该车型后悬架为多连杆类型，对左右拖曳臂单独进行分析，在满足精度的前提下可以提高计算效率。单侧模型的硬点数为7个，一共42个通道。应用惯性释放计算各个通道单位载荷下的应力分布，结合新建焊缝数据库及疲劳分析软件Femfat计算出强化路面下的疲劳损伤分布。

计算结果显示，损伤最大位置位于制动器安装板端部的三角加强板T型焊缝处，如图9，损伤值大小为1.2，超过目标值1，与路试中此处发生开裂相吻合，有效地预测了焊缝存在的失效风险，如图10，减振器轴向阻尼力造成了该处焊缝的拉伸撕裂。

5 结束语

本文根据某公司自身焊缝标准建立了30%焊透率的T型焊缝数据库，并对疲劳分析软件Femfat焊缝数据库进行了扩充，利用Neuber及Radaj的焊缝缺口分析理论，有效的应用于工程实践中，具有以下优点：

（1）根据用户自身需求，实现了更多类型的焊缝数据库拓展，为焊缝的疲劳分析提供了理论参数。

（2）利用Neuber提出的虚拟缺口理论及Radaj缺口系数有限元分析法得到焊缝的焊根、焊趾处的应力集中系数，结合道路谱得到焊缝局部真实应力历程，为焊缝的评估提供了一种有效的方法。

（3）新增焊缝数据库能有效预测焊缝的失效，为项目前期的产品改进提供理论依据，能有效节约开发成本，缩短开发周期。

参考文献：

[1]Radaj D， Sonsino C.M， Fricke W. Fatigue assessment of welded joints by local approaches [M]. Woodhead Publishing and Maney Publishing， Cambridge，2006.

[2]李运超.基于整车虚拟试验场的后悬架疲劳分析[D].同济大学，2009：25-38.

[3]胡玉梅，陶丽芳，邓兆祥，等.车身台架疲劳强度试验方案研究[J].汽车工程，2006，28（3）：301-303.

[4]黄鹏程，柳杨，陈伟.副车架疲劳台架试验的有限元模拟[J].计算机辅助工程，2006，15（S1）：193-194.

[5]Radaj D， Lazzarin P， Berto F. Generalized Neuber concept of fictitious notch rounding [J]. International Journal of Fatigue，2013，51：105-115.

[6]Radaj D， Sonsino C.M， Fricke W. Recent developments in local concepts of fatigue assessment of welded joints [J]. International Journal of Fatigue， 2009，31：2-11.

[7]Radaj D， Lazzarin P， Berto F. Fatigue assessment of welded joints under slit-parallel loading based on strain energy density or notch rounding [J]. International Journal of Fatigue， 2009，31：1490-1504.

[8]Radaj D， Berto F， Lazzarin P. Local fatigue strength parameters for welded joints based on strain energy density with inclusion of small-size notches[M]. Engineering Fracture Mechanics， 2009，76：1109-1130.

[9]Radaj D， Sonsino C.M， Fricke W. Recent developments in local concepts of fatigue assessment of welded joints [J]. International Journal of Fatigue， 2009，31：2-1.

[10]H. Dannbauer， C. Gaier， K. Hofwimmer"Fatigue Analysis of Welding Seams and Spot Joints in Automotive Structures"， SAE 2005-01-1323.

[11]朱明武，李永新，卜雄洙.测试信号处理与分析[M].北京：北京航空航天大学出版社，2006：169-220.