基于小班化教育模式下七年级数学头脑风暴教学法的探究

◎杨家乐

一、“头脑风暴教学法”的概述

1.“头脑风暴教学法”的缘由

头脑风暴法（Brainstorming）是由美国创造学家奥斯本（A.F.Osbron）于1939年首次提出、1953年正式发表的一种在小组讨论中普遍采用的旨在激发创造性思维的方法。头脑风暴法让所有参加者在自由愉快、畅所欲言的气氛中，自由交换想法或点子，并以此激发创意及灵感，使各种设想在相互碰撞中激起脑海的创造性“风暴”。

“英国英特尔未来教育”提出把头脑风暴法作为一种教学法，尝试通过聚集学习者自发提出的观点，产生一个新观点，进而使学习者之间能够互相帮助，促进合作式学习，能够在学习的过程中，取长补短，集思广益，共同进步。

二、阐述小班化教育模式下七年级数学头脑风暴教学方法的有效实施

1.以浙教版七年级数学上册第五章第一节《一元一次方程》为例，简述小班化教育模式下头脑风暴教学方法的实施

（一）故事预设，生成创新

借助多媒体辅助手段创设故事情境，教师解说引导，启迪学生发现寓意，鼓励学生大胆创新，跳出思维定势的牢笼，不做“被训化的跳蚤”。

通过“马戏团跳蚤”这一故事进行教学预设，充分调动学生发散思维的积极性，进而生成“头脑风暴教学”的学生准备。

（二）创设情境，以旧引新

通过创设“小小数学实验室”的教学情境，引导学生回顾等式的定义，在探索实践中建立“方程”模型，揭示“数学来源于生活，又作用于生活”的新课程理念。

（三）头脑风暴，探究新知

（1）寻找生活中的方程，自由畅谈

富有趣味性、联系生活实际的情境材料设计是激发学生思考的兴奋剂。学生按学习小组开展讨论，教师参与学生小组的学习并适度鼓励，引导学生进行自由讨论，自由想象，自由发挥，让组员间相互启发，并认真倾听其他同学发言，能够做到知无不言，言无不尽，真正畅所欲言。

（2）第一次“头脑风暴”，引生入胜

维果茨基的“最近发展区”理论在数学教学过程中的运用，既符合学生的认识规律，也符合学生的心理发展规律。通过实际情境问题的创设在学生“现有发展水平”和“潜在发展水平”之间的“最近发展区”，学生的“现有发展水平”是已经学习的方程知识，通过观察讨论、头脑风暴，归纳出“一元一次方程”，能够让学生从“最近发展区”向“潜在发展水平”转化，从而使学生的思维向更高层次发展。

（3）第二次“头脑风暴”，拓展提升：

1）做一做：灵活运用，拓展提升

①关于x的方程3xm-2+5＝0为一元一次方程，那么代数式

②方程（a+6）x2+3x-8＝7为关于x的一元一次方程，那么

2）找一找：尝试检验，提升拓展

通过尝试对于一些较简单方程的检验，能够确定未知数的较小的一个取值范围，然后将这些可取到的值代入方程进行检验。

3）做一做：检验求解，提升拓展

引导利用检验法和等式的基本性质解一元一次方程，启发引导学生多角度思考问题，开阔了学生的思路。通过头脑风暴法，帮助培养学生的发散思维能力和创造能力。

2.运用头脑风暴教学法进行七年级数学一题多解教学，培养学生的敛散思维能力。

教学中要善于运用头脑风暴教学法，引导学生尝试“一题多解”，激发学生的潜能，促进学生创造性思维发展，并且培养学生的敛散思维能力。

掌握全等三角形的判定方法，拓展解题思路，灵活运用，融会贯通，建构知识网络，多方面证明三角形的全等。

（一）全等三角形的判定方法

①定义法：两个能够重合的三角形是全等三角形

②边边边：三条边对应相等的两个三角形是全等三角形（SSS）

③角边角：两个角和它们的夹边对应相等的两个三角形是全等三角形（ASA）

④角角边：两角和其中一角的对边对应相等的两个三角形全等（AAS）

⑤边角边：两边和它们夹角对应相等的两个三角形全等（SAS）

（二）解题思路

①已知两边：找夹角（SAS）

找另一边（SSS）

②已知一边一角，并且角为该边的对角：找任一角（AAS）

③已知一边一角，并且角为该边的邻角：找夹角的另一边（SAS）

找夹边的另一角（ASA）

找边的对角（AAS）

④已知两角：找夹边（ASA）

找对边（AAS）

（三）例题解析

如图所示，已知D、E是△ABC中BC边上的两点，AD＝AE，请你再附加一个条件，使△ABE≌△ACD。

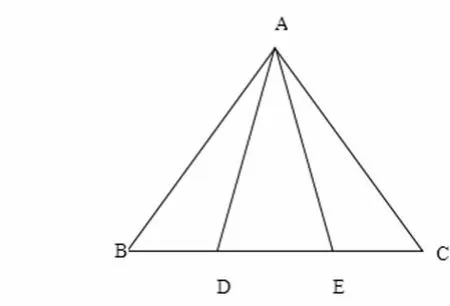
解法一：添加条件BD＝CE，因为BD＝CE，所以 BD+DE＝CE+DE，即 BE＝CD；又因为 AD＝AE，所以∠AEB＝∠ADC，在△ABE和△ACD中，AD＝AE，BE＝CD，∠AEB＝∠ADC，所以△ABE≌△ACD（SAS）。

解法二：添加条件△ABC是等腰三角形，AB＝AC，因为AD＝AE，

所以∠AEB＝∠ADC，因为AB＝AC，所以∠B＝∠C，在△ABE和△ACD中，AD＝AE，∠B＝∠C，∠AEB＝∠ADC，所以△ABE≌△ACD（AAS）。

解法三：添加条件∠BAD＝∠CAE，因为∠BAD＝∠CAE，

所以∠BAD+∠DAE＝∠CAE+∠DAE，即∠BAE＝∠CAD，又因为AD＝AE，所以∠AEB＝∠ADC，在△ABE和△ACD中，AD＝AE，

∠BAE＝∠CAD，∠AEB＝∠ADC，所以△ABE≌△ACD（ASA）。

解法四：添加条件BD＝CE，因为BD＝CE，所以BD+DE＝CE+DE，即BE＝CD；又因为 AD＝AE，所以 ∠AEB＝∠ADC，则有 ∠ADB＝∠AEC，在△ADB和△AEC中，AD＝AE，∠ADB＝∠AEC，BD＝CE，所以△ADB≌△AEC（SAS），所以 AB＝AC；在△ABE和△ACD中，AB＝AC，AD＝AE，BE＝CD，所以

△ABE≌△ACD（SSS）。

根据七年级数学中《一元一次方程》的教学研究案例和一题多解问题的解题策略，模拟了小班化教学环境，探究头脑风暴教学法应用的前瞻性和效用性。小班化教育模式下的头脑风暴教学法注重因材施教、灵活教学，有助于培养学生的创新实践能力和敛散性思维能力，这是对初中数学教学法的创新与突破。