数据挖掘关联规则在词语关联度计算中的应用

董晨辉，师文慧

(福建宁德核电有限公司，福建 宁德 355200)

0 引言

随着大数据时代的到来，数据挖掘引起了信息产业界的广泛关注。关联规则作为数据挖掘的一个研究方向，广泛应用于销售行业，如：购物篮分析、分类设计、捆绑销售和亏本销售分析等。它是以大规模事物关系库为基础，发现其项集之间频繁出现的模式、关联和相关性。

移动通信技术与社交媒体的发展，使得中文短文本形式的信息广泛渗透于社会和生活的各个领域。由于这些短文本字数较少，因而所描述的概念信号弱、特征信息模糊，单从字面上难以获取有效的特征信息，需要对文本进行更深层次的分析。

词语的关联度计算已应用到信息检索、人工智能等多个领域，为文本信息挖掘和自然语言处理奠定了基础。但传统的方法对关联度计算所度量的关系不明确，多数以相似度为基础，而相似度只是关联度的一个特例，只包括词语之间的上下位关系和同义关系，易造成关联度计算的局限性和不准确性。

由于词语特征信息稀疏，因此计算词语间关联度是一项复杂而艰难的任务，需要大量的外部资源作为支撑，以便对词语特征进行扩充。有些方法是以外部知识库为基础来计算词语间关联度[1]，有些方法是通过对大型语料库进行统计分析来实现[2]，有些方法则使用经过手工处理得出的语汇结构实现，如同义词典[3]、HowNet[4]。这些方法均没有涉及数据挖掘的关联规则。

因此，本文以新闻语料为外部数据库，提出了一种利用数据挖掘中关联规则来计算词语之间的关联度的计算方法，以挖掘各词语之间频繁出现的关联性。

1 关联规则介绍

关联规则挖掘问题是Agrawal R等人于1993年首先提出来的[5]，是指从巨量的信息资源中寻找隐含在数据项集间的有趣联系或关联关系，描述在一个事务中的物品之间同时出现的规律的知识模式。其表达式为：设I={i1，i2，i3，…，im}是所有项的集合；设D是事务T的集合，其中每个事务T是项I的子集，使得T⊂I。其包含的相关概念如下。

①支持度：事务集D中包含XUY的百分比。

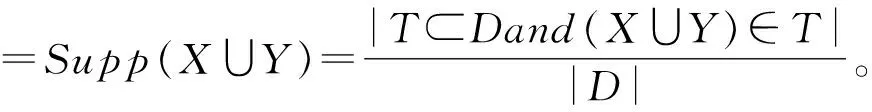
(1)

其中，|D|等于D中事务T的个数。

②置信度：在含有物品X的事务T中含有物品Y的概率。

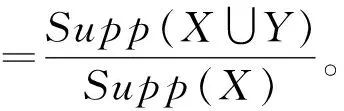
(2)

③期望可信度：无任何条件影响下，物品X在事务集D中出现的概率。

(3)

④作用度：描述物品X对物品Y的影响力，反映了Y对于X的依赖程度。

(4)

⑤关联规则挖掘：从事务集合中挖掘出满足支持度和置信度最低阈值(minsup，minconf)要求的所有关联规则，这样的关联规则也称强关联规则。

⑥频繁项集(frequent itemsets)。如果项集的频率大于“最小支持度×D中的事务总数”，则称该项集为频繁项集[6]。

2 词汇社区结构的构建

关联规则的挖掘过程主要包含两个阶段：第一阶段，先从资料集合中找出所有频繁项集；第二阶段，由这些高频项目组中产生关联规则，即满足最小支持度和最小置信度的规则。

利用关联规则计算短文本的关联度，这一类方法的理论基础是Firth在文献[7]提出的上下文假设：词汇的上下文环境体现的是人们在实际语言交流中使用该词汇的具体途径，并且两个词汇的使用方式越接近，在语义上就越相关。基于这一理论便可以通过统计大规模语料中词汇出现的规律得到词语间的关联度，即通过在大规模语料中统计词汇所处的上下文环境，得到每个词汇的上下文分布，而两个词汇的语义相关度则通过比较二者对应的上下文分布并综合分析后得出最终结果。

关联规则一般用来发现交易数据库中不同商品(项)之间的联系。将大规模语料库(人民日报2013-2014年语料库)作为交易数据库，每篇新闻中出现的实词集合作为事务，出现的每个词语认为是商品，便可以找出两词语间的联系。在中文语料中，将交易中的频繁项集认为是关联度高的词汇所构造的一个词汇社区，根据人民日报2013-2014年语料库构造的社区结构就是新闻中共同出现频率高的词语集合，词汇社区结构如图1所示，其中椭圆的大小代表社区的大小，椭圆的包含关系代表社区的包含关系。

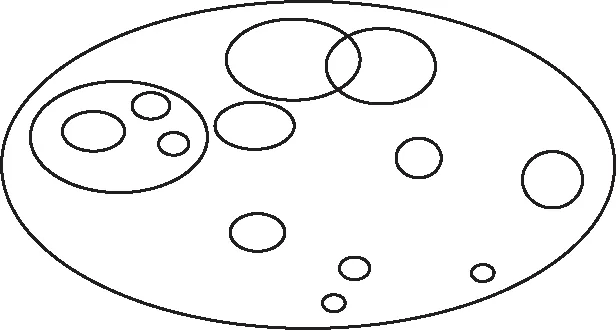
图1 词汇社区结构

构造词汇社区结构作为关联规则挖掘的第一阶段，它的原理是根据k-频繁项集生成(k+1)-频繁项集。主要任务是从原始资料集合中找出频繁项集。频繁的意思是指某一项目组出现的频率必须达到某一水平，即其支持度不小于最小支持度(minsup)。以一个包含A与B两个项目的2-itemset为例，根据公式(1)可求得包含{A，B}项目组的支持度，若支持度大于等于所设定的最小支持度这一阈值时，则{A，B}称为频繁项集。一个满足最小支持度的k-itemset，则称为k-频繁项集，一般表示为Large k或Frequent k。算法是从Large k的项目组中再产生Large(k+1)，直到无法再找到更长的频繁项集为止，这样一个词汇社区结构就形成了。

3 选用的算法

Apriori算法和FP-tree算法是关联规则挖掘中最经典的两个算法，前者采用逐层搜索的迭代策略，先产生候选集，再对候选集进行筛选，然后产生该层的频繁集；后者采取模式增长的递归策略，不用产生侯选集，而是把事务数据库压缩到一个只存储频繁项的树结构中。FP-growth算法是韩家炜等人在2000年提出的关联分析算法[8]，算法基于Apriori算法构建，但采用了高级的数据结构以减少扫描次数，在不生成候选项的情况下，完成Apriori算法的功能，大大加快了算法速度。因此，本文选择FP-growth算法进行词语关联度的计算。FP-growth算法发现频繁项集的基本过程如下。

3.1 构建FP树

构建FP树，即是把事务数据表中的各个事务数据项按照支持度降序排序后，依次插入到一棵以NULL为根结点的树中，同时在每个结点处记录该结点出现的支持度。图2为构建FP树的过程示意图。

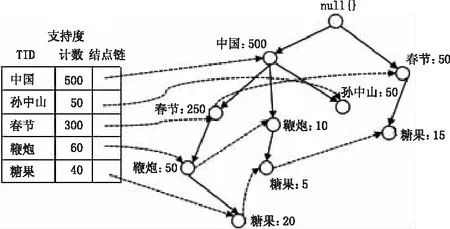
图2 构建FP树的过程示意图

①输入：数据集、最小值尺度。输出：FP树、头指针表(inTree，headerTable)。遍历数据集，统计各元素项的出现次数，创建头指针表。②移除头指针表中不满足最小值尺度的元素项。③第二次遍历数据集，创建FP树。对每个数据集中的项集：第一，初始化空FP树；第二，对每个项集进行过滤和重排序；第三，使用这个项集更新FP树，从FP树的根节点开始，如果当前项集的第一个元素项存在于FP树当前节点的子节点中，则更新这个子节点的计数值；否则，创建新的子节点，更新头指针表。对当前项集的其余元素项和当前元素项的对应子节点递归第三的过程。

3.2 从FP树中挖掘频繁项集

3.2.1 算法1：通过构造条件树查找频繁项集

①从FP树中获得条件模式基；②利用条件模式基，构建一个条件FP树；③迭代重复步骤①和步骤②，直到树包含一个元素项为止。

其中的条件模式基是指包含FP-Tree中与后缀模式一起出现的前缀路径的集合，也就是同一个频繁项在PF树中的所有节点的祖先路径的集合。比如在图2中糖果在FP树中一共出现了3次，其祖先路径分别是{中国，春节，鞭炮：20(频度为20)}，{中国，鞭炮：5}和{春节：15}。这3个祖先路径的集合就是频繁项“糖果”的条件模式基。然后，将所获得的条件模式基按照FP-Tree的构造原则形成一个新的FP-Tree，称为条件树，如图3所示。

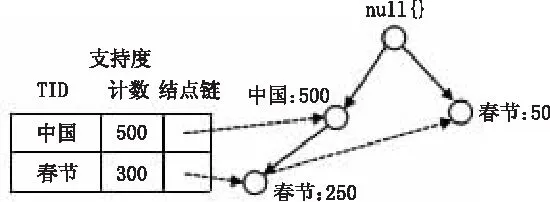
图3 条件树示意图

3.2.2 算法2：递归查找频繁项集

输入：有当前数据集的FP树(inTree，headerTable)。

①初始化一个空列表preFix表示前缀。②初始化一个空列表freqItemList，接收生成的频繁项集(作为输出)。③对headerTable中的每个元素basePat(按计数值由小到大排列)进行递归：记basePat+preFix为当前频繁项集newFreqSet；将newFreqSet添加到freqItemList中；计算t的条件FP树(myCondTree，myHead)；当条件FP树不为空时，继续下一步，否则退出递归；以myCondTree，myHead为新的输入，以newFreqSet为新的preFix，外加freqItemList，递归这个过程。

4 词语间相关度的计算

本文基于数据关联规则挖掘提出计算词语间关联度的方法。记|D(X)|为含有词语X的新闻报道的篇数，可得出：

(1)词语A，B的支持度反映词语A与B的共现程度。如果A与B同时出现的概率小，说明A与B的关系不大；如果A与B共现频率较高，则说明A与B是相关的。

(5)

其中，|D|等于数据库D中新闻报道的总篇数；|D(A∪B)|为数据库中共同含有词语A和B的新闻报道的篇数。

(2)一部分词对在重要程度上是不对称的，例如，“中国”和“北京”相互之间的依赖程度是对称的，因为“北京”是“中国”的首都；相反，位于四川省邛崃市的“白杨村”和“中国”相互之间依赖程度是不对称的，“白杨村”对“中国”的依赖程度大于“中国”对“白杨村”的依赖程度。A出现时B出现的概率可用词语A，B的置信度来表示。置信度“A⟹B”并不等于置信度“B⟹A”。

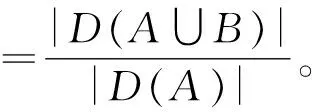
(6)

(3)期望可信度描述了在所有报道中词语A出现的概率。

(7)

(4)词语A对B的作用度描述了A对B的影响力的大小。作用度越大关联性也就越强。一般情况，只有关联规则的置信度大于期望可信度，才说明A对B有促进作用，也说明它们之间存在某种程度的关联性。如果作用度值等于1，说明两个条件没有任何关联；如果小于1，说明在词语A出现的前提下，词语B出现的概率降低，即词语A对词语B并没有促进作用，词语A与词语B是相斥的。一般在数据挖掘中当作用度大于3时，才承认挖掘出的关联规则是有价值的。

(8)

结合词语A，B之间的支持度以及置信度，可以给出计算两词语关联度的计算公式：当Lift(A⟹B)和Lift(B⟹A)其中有一个为零，词语A与词语B的关联度记为0；当Lift(A⟹B)>1并且Lift(B⟹A)>1时，词语A与B之间的关联度计算公式为：

(9)

5 实验验证

5.1 数据准备

在数据挖掘这一过程中，数据准备作为第一步，也是这一过程中的核心。数据挖掘的处理对象是大量的数据，数据准备是否做好直接影响到数据挖掘的效率和准确度，以及最终结果的有效性。

数据集选择的是人民日报2013-2014年语料库，语料库为已标注好的新闻报道，但并不适合直接在这些数据上进行数据挖掘，仍需要对语料进行清洗加工。词语关联度主要针对于有实际意义的特征词，因此第一步净化包含的步骤主要有去停用词、过滤虚词等；第二步为缩减，主要目的为消除新闻报道中重复的词语，消除冗余数据；第三步为转换，主要是将经过加工处理的语料转换成数据库文件，然后在此基础上进行数据挖掘。关于词语关联度计算的测试集选用了人工翻译WordSimilarity-353测试集[9]以及北京理工大学所统计的Words-240[10]。

5.2 实验过程

本实验硬件环境为双核T6 Intel处理器、主频2.80 GHz、内存为4 GB，编程环境为MyEclipse，数据库使用的是MySQL。通过挖掘强关联规则，可以拓展词语的长度，增加特征数，从而减轻特征稀疏性对关联度计算结果产生的影响。

社区规模可以通过设置不同的最小支持度以及最小置信度来改变。规模较小的社区包含了紧密的语义相关的互联节点，它们通常隶属于同一主题。社区结构规模与支持度阈值的关系如图4所示。利用“试错”法选取合适的阈值，支持度越大，社区规模越小，语义节点间也更为紧密。

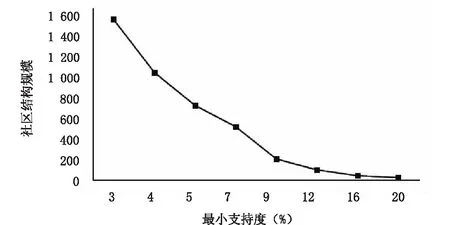
图4 社区结构规模与支持度阈值的关系图

5.3 实验结果与分析

根据上述计算方法，实现了关联规则在词语关联度计算中的应用。部分词对关联度的计算结果如表1所示。

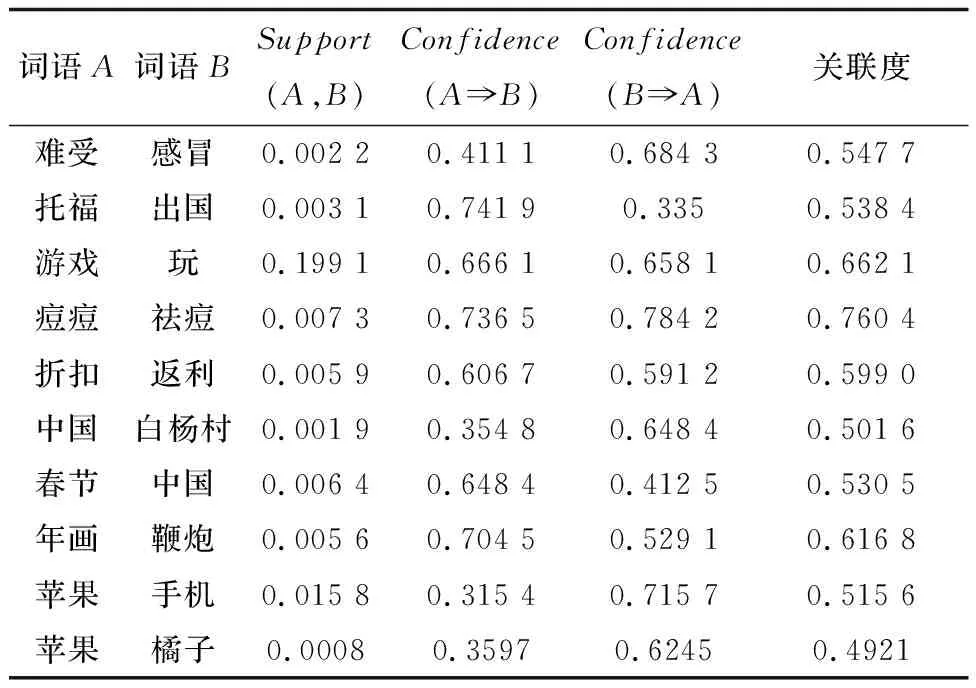
表1 部分词对关联度计算结果

通过分析表1，可以看出实验结果有一定的合理性，符合人们主观上的判断。

(1)该计算方法解决了依赖程度不对称词语间关联度的计算问题，例如“中国”与“春节”，“春节”对于“中国”的依赖程度高于“中国”对于“春节”的依赖程度。

(2)从计算结果可以看出词语的支持度都比较小，这是由于新闻语料中出现的词语过于庞大造成的，但支持度的大小并不影响关联度计算的结果。

(3)该计算方法是通过对大规模语料库进行统计分析从而得到词语间关联度，因此没有考虑词语语义这一层面，例如“苹果”与“橘子”、“苹果”与“手机”这两个词对中“苹果”的语义并不相同，但在计算时并不考虑深层的语义信息。

图5为该计算方法与WikiRelate[11]，ESA[12]和WLM[13]计算准确率的对比结果，表2为该计算方法与WikiRelate[11]，GooRel[14]方法所计算出的Spearman相关系数的对比。从图5可以看出本文计算方法的准确率为84%，比其他方法都高。从表2可看出该方法的Spearman相关系数比另两种方法高。准确率以及Spearman相关系数的提高说明数据挖掘的关联规则对词语关联度计算是有一定帮助的，证明了该方法的可行性。

图5 准确率对比

算法Spearman相关系数Sim0.795WikiRelate0.776GooRel0.731

6 结语

本文采用数据挖掘的关联规则中运行速度较快的FP-growth算法，目的是从大规模语料库中得到词汇社区网络。目前数据挖掘大部分应用在银行、金融、大型商业数据库等盈利性领域中，在词语关联度这一研究领域中应用很少，本文对数据挖掘的关联规则在词语关联度计算的应用进行了探索，提高了词语关联度计算的准确性，在后续工作中，我们将进一步研究如下问题：

(1)人民日报新闻语料过于正规、范围局限，因此可以考虑扩大语料范围，例如网络上的微博语料库等。

(2)本文研究的词语关联度计算是基于语料库的，该算法是通过对大量文本进行统计分析来得出词语关联度。下一步工作可以与基于外部知识库的方法结合起来，例如维基百科、知网等。通过对知识库结构化的、明确的语义知识进行分析，提高词语关联度计算的覆盖度和准确性。

(3)在本文的研究基础上，希望将数据挖掘的关联规则应用在自然语言处理其他研究任务中。

参考文献：

[1] LENAT D B， GUHA R V. Building large knowledge based systems[M]. New York：Addison Wesley，1990：78.

[2] DEERWESTER S， DUMAIS S， FURNAS U， et al. Indexing by latent semantic analysis[J]. Journal of the American society for information science，1990，41(6)：391-407.

[3] ALEXANDER B， GRAEME H. Evaluating word net-based measures of lexical semantic relatedness[J]. Computational linguistics，2006，32(1)：13-47.

[4] 李赟.基于中文维基百科的语义知识挖掘相关研究[D].北京：北京邮电大学，2009.

[5] DAVIS R， LENAT D B. Knowledge-based systems in artificial intelligence[M]. New York： McGraw-Hill，1982：39-51.

[6] AGRAWAL R， IMIELINSKI T， SWAMI A N. Mining association rules between sets of items in large databases[C]// Proceedings of the 1993 ACM Sigmod Intenrational Conference on Management of Data， Acm sigmod record，1993，22(2)：207-216.

[7] FIRTH J R. A synopsis of linguistic theory 1930-55[M]. Oxford： The Philological Society，1957：1-32.

[8] HAN J， PEI J， YIN Y. Minning frequent patterns without candidate generation[J]. Acm sigmod international conference on management of data，2000，29(2)：1-12.

[9] FINKELSTEIN R L. Placing search in context： the concept revisited[J]. Acm transactions on information systems，2002，20(1)：116-131.

[10] 夏天.中文信息处理中的相似度计算研究与应用[D].北京：北京理工大学，2005.

[11] STRUBE M， PONZETTO S P. WikiRelate! computing semantic relatedness using wikipedia[J]. Proc. Nat. Conf. artificial intelligence(AAAI)，2006，2(6)：1419-1424.

[12] GABRILOVICH E， MARKOVITCH S. Computing semantic relatedness using Wikipedia-based explicit semantic analysis[J]. Proc international joint conference on artificial intelligence，2007(6)：1606-1611.

[13] MILNE D. Computing semantic relatedness using Wikipedia link structure[C]. Proceedings of the New Zealand Computer Science Research Student conference，2007.

[14] SPEARMAN C. The proof and measurement of association between two things[J].The American journal of psychology，1904，15(1)：72-101.