基于CFD的涡扇发动机推阻分解方法及应用

张宇飞, 陈海昕, 方晓明

(清华大学 航天航空学院, 北京 100084)

0 引 言

现代飞机的设计和制造日趋精细化，研制过程强烈依赖于多家制造商的分工协作。飞机机体与发动机这两大部件一般都由不同公司完成研制。在真实飞行中，飞机和发动机安装在一起，一方面受到各自的气动阻力，另一方面会产生新的干扰阻力。但是飞行试验仅能测得推力与阻力的合力，必须采用辅助手

段标定推力和阻力。在平衡飞行状态下，飞机的推力与阻力大小相等，方向相反，所以发动机推力大小的确定会影响真实飞行升阻比的判断，从而影响着民用客机的市场竞争力。在极端情况下，飞行包线边界处还可能出现推力不能克服阻力的情况，此时就更需要定量分析推力与阻力。飞行推力与阻力的确定长期以来一直受到国外飞机和发动机公司的重视，美国Society of Automotive Engineers(SAE)针对涡扇发动机、螺旋桨、涵道风扇、推力矢量发动机等，均出台了一系列标准可供参考，比如AIR1419、AIR1678、AIR1703、AIR4065、AIR5450、AIR5771、AIR6007等。并且这些标准一直随着技术发展在持续更新，以AIR1703[2]为例，在1985年出了第一版之后，又在2012年重新制定了修订版。

推阻分解方法(Thrust/Drag Bookkeeping)是SAE AIR1703标准中确定飞行中推力和阻力的一种通用方法[1-2]，该方法能够定量计算作用在飞行系统内的气动阻力和发动机推力，提出一种飞机和发动机制造商都能够认可的推力/阻力分解方案，并获得一套不依赖于发动机油门状态的飞机配平升力、阻力曲线[2]。此方法已经得到波音、通用电气、普拉特·惠特尼、罗尔斯·罗伊斯等国外飞机和发动机公司的认可，并在波音777飞机研制中应用[2]。然而在国内，由于民用飞机的发展相对落后，推阻分解方法的研究和应用还相对较少，尚缺乏一种行业通用的飞机和发动机公司均能接受的推力和阻力计算方法，同时也缺乏可靠的标准算例数据供试验和数值计算作为验证参考。

推阻分解方法的主要原理是利用流体力学的控制体理论，针对发动机短舱的内外流道分别进行控制体分析，辨别推力与阻力产生的区域[3-4]。在一般的推力/阻力划分体系下，发动机短舱外罩的阻力算做飞机阻力；进气道和内外涵喷管的阻力算做发动机的推力损失[5]，其损失大小决定于发动机的设计水平；机体与发动机安装后的干扰造成的额外推力损失(如喷流与挂架的干扰、外流速度对喷流的抑制作用等)称为干扰阻力，计入飞机阻力范围[2]。Dusa等人[6]给出了各项损失的大小范围，其中风扇喷管的推力损失约占总推力的0.5%～0.8%，核心机喷管的损失约0.2%～0.3%，喷流作用在挂架上的冲刷阻力约0.5%～1.0%，气流膨胀、喷流/挂架/机翼之间的干扰等损失约0.3%～0.9%。进气道阻力和喷管/后体的阻力均与发动机状态相关，被称为油门依赖力，进气道溢流阻力和喷管/后体的喷流效应阻力均属于此类。为了确定飞行状态的气动力，一般需要选取一个典型状态作为参考状态，获得该状态的详细气动力参数，其他飞行状态即在此状态下附加油门依赖的气动力。为了保持飞机设计过程的一致性，推阻分解需要遵循的准则有[1]：

1) 所有部件受力不能遗漏也不能重复；

2) 分解方法应尽量反映部件性能；

3) 选定的参考状态应接近飞行状态，且具有可行的修正方法；

4) 从初步设计直到飞行试验中推阻分解方法应保持统一，以便追溯研制过程的性能变化。

推阻分解的核心是准确计算发动机的推力损失。在发动机设计过程中，发动机推力及损失可以由地面试车台或者高空模拟试车台确定[2]。两种方式下发动机进气道均需要采用钟形罩进行引流，并保持短舱外罩流速接近于0。推力测量装置与钟形罩不连接，以排除进气阻力的影响。采用这样的测试设备，可以尽量排除短舱外罩阻力对推力的干扰，获得发动机的净推力，并确定进气道和喷管的推力损失，最终获得喷管的两个重要的性能系数：流量系数和速度系数(也称作推力系数)。在飞行状态下，可以利用地面测试所获得的流量系数和速度系数，以及飞行温度、压力、速度等参数，计算飞行状态的发动机推力。为了获得更准确的推力数据，地面测试获得的性能系数需要经过一系列的修正才能用于飞行推力的确定[2]。但是，修正也仅考虑了飞行的外流速度对于喷管流量的抑制效应，而忽略了外流速度对于速度系数的影响[7]。在通行的推阻分解框架下，外流速度对于速度系数的影响所带来的损失归于飞机阻力部分，并得到了飞机公司的认可[2]。

随着计算流体力学(CFD)技术和计算机硬件技术的发展，飞行器设计越来越依赖数值仿真。采用CFD方法进行推阻分解，可以很大程度上避免试验测试的设备限制、尺度效应以及误差修正问题，能够尽可能接近飞行状态，为机体/动力集成带来极大便利。近年来，基于CFD的推阻分解计算精度研究在国外已经逐渐成为了一个研究热点，美国航空航天学会(AIAA)自2011年至今已经开展了三届推进空气动力研讨会(Propulsion Aerodynamics Workshop，PAW)，其主要目的就是探讨CFD方法对于喷管推力损失的计算精度，着重关注流量系数和速度系数的计算误差。第一届PAW的算例是一个简单的轴对称收缩喷管[8-10]，第二、三届算例是民机双涵道发动机喷管[11-12]。

然而在国内，对这方面研究的关注还相对较少，相关文献并不多见。本论文主要开展基于CFD方法的推阻分解研究，首先介绍推阻分解的控制体分析方法及原理，然后采用三个典型算例进行推阻分解方法进行应用验证，分析和验证CFD方法对于推阻分解的计算效果，为飞机设计提供参考。

1 发动机短舱控制体受力分析

针对典型的民用航空发动机，推阻分解的控制体分析时一般不考虑核心机的旋转部件。现代民机为了提高推进效率，一般采用高涵道比发动机，喷管分为内涵和外涵两个流道，图1显示了一个典型的民用发动机的控制图示意图。以唇口驻点为分界线，进入发动机内部的流体产生推力，从外部流过的流体产生阻力。如图1所示，控制体可以分为三个区域：进气流管(从E0到E1截面)；发动机机体区域(从E1到E8和E18截面)；喷流流管(E8到E9截面，E18到E19截面)。

在发动机具有外流速度的状态下，根据受力关系，可知发动机的净推力FNPF为：

(1)

根据控制体表面的受力平衡关系，尾迹区从E8/E18到E9/E19截面的受力平衡可表示为式(2)，入口从E0到E1截面的受力平衡可以表示为式(3)。其中u9和u19分别表示E8和E18截面流体自由膨胀到环境大气后的速度，u0表示自由来流气体的速度；ΦPost和ΦPre分别为尾迹和入口流管的侧面受力。

(2)

(3)

整理上述式(1)～式(3)，可以得到发动机净推力如式(4)，这也是选取E0到E19截面间的区域作为一个控制体的受力形式。

(ΦPre+ΦExt+ΦPost)

=FN-D

(4)

在试车台试验中，发动机性能标定过程均尽量保证短舱外部的流速接近0，并且采用钟形罩将进气流管的作用力分离，因此可近似认为ΦPre=ΦExt=0，定义此时的净推力为Fc。

=Fc

(5)

(6)

(7)

由于外流速度的不同，试车台状态和飞行状态的流动具有较大的差异。但是如引言所述，在通行的推阻分解方法中隐含了一个约定，即仅计入外流速度对于喷管流量的抑制效应，而忽略了外流对于速度系数的影响，这种方式的误差所带来的推力损失由飞机公司承担[2]。在这个约定下，ΦPost被忽略，就可以采用试验测试所获得的速度系数用于求解飞行状态下的推力损失。此时试验测试的推力系数可表达为：

(8)

所以在飞行状态时，发动机的总净推力FN为式(9)，而气动阻力相应为式(10)。其中Cv由地面测试而来，而FNPF采用全机合力测量获得。

(9)

D=FN-FNPF

(10)

从速度系数的表达式可知，发动机喷管的推力损失已经在速度系数中反映出来了。式(6)给出的是内外涵道混合的速度系数，而在真实发动机设计过程中，一般还需要针对内、外涵道分别计算各自的速度系数，用于判断各自的推力损失。此外，进气道和喷管的流量系数也是发动机设计过程的重要参数，它可以表示不同来流速度下外流对于喷管的流量抑制效应，对于飞行试验的流量修正具有重要作用。但对于CFD计算而言，实际流量可以通过计算网格进行精确积分，因此对于推阻分解的精度影响相对较小。

综合上述分析，基于CFD方法的推阻分解过程分为三个步骤：首先进行地面状态分析，获得喷管性能参数(流量系数和速度系数)；然后进行飞行状态的全机推阻合力分析；最后将地面状态的性能参数用于推阻分解计算，最终获得气动阻力。

2 算例及应用

推阻分解方法可以应用于进/排气系统的阻力分析，如进气道溢流阻力和喷管喷流推力损失分析，以及机翼与动力短舱之间的干扰评估等。本节采用三个算例对本文方法进行验证和测试。第一个是NACA 1-85-75进气道算例，验证方法对于单独进气道溢流阻力的计算效果；第二个算例是PAW2双涵道喷管，分析本文计算方法对于喷管性能预测的效果；第三个算例是NAL-AERO-02-01动力短舱算例，包含了进/排气性能，对基于CFD计算的推阻分解方法进行验证和分析。

2.1 NACA 1-85-75进气道算例

进气道溢流阻力的分析是机体/动力一体化集成的重要方面，主要关心进气道在不同流量系数下的进气道阻力性能，在动力集成中用于不同发动机推力状态之间的性能修正。张美红等[13]和张兆等[14]采用CFD方法进行溢流阻力计算分析，可作为溢流阻力计算方法的参考。本文为了测试推阻分解方法在溢流阻力计算上的效果，采用NACA 1-85-75进气道进行验证。NACA 1系列进气道是NACA早期设计的高临界速度的进气道[15]，拥有较多的试验数据[16-17]可供CFD计算参考，其编号中的1表示系列，85表示喉道直径为外罩最大直径的85%，75表示从唇口到最大直径处的长度为最大直径的75%。

由于NACA 1-85-75进气道算例是轴对称外形，且不考虑攻角变化，因此可以采用轴对称方法进行计算。计算模型的最大直径为45.72 cm，长度为34.29 cm，喉道直径为38.86 cm，唇口与喉道的面积之比为1.009，具体模型外形和安装方式可见文献[16]。计算网格如图2所示，二维截面网格总数约76 000点。为了减小边界条件对计算结果的影响，上游远场边界与唇口的距离为500 cm，下游进气道的出口采用等直段延伸100 cm。壁面第一层网格的法向距离为0.0002 cm，以保证第一层的y+小于1。由于模型具有轴对称的特点，圆周方向仅计算3°角的扇形区域，网格采用二维网格旋转而成。

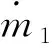
图4显示了几个不同流量系数下的马赫数分布云图和流线图。可以看出，当φ=0.2时，短舱外壁面已经出现明显的流动分离；随着流量系数的增加，φ=0.4时流动分离消失，但由于溢流效应的影响，表面出现明显的激波；流量系数继续增加，激波削弱，直至φ=0.8时激波和流动分离均消失，流场特性较好。

为了定量分析不同来流速度下的溢流阻力特性，本文分别计算了Ma=0.60、0.85、0.94和1.20四个速度下的不同流量系数，基于进气道外罩最大直径的雷诺数分别为4.5×106、5.4×106、5.5×106、5.7×106。

图5给出了不同马赫数下φ=0.60的短舱外罩表面压力分布与试验结果的对比。从图上可以看出，不同马赫数下压力分布均与试验结果吻合良好。在Ma=0.60时，由于溢流造成的表面加速，使进气道前缘出现了明显的吸力峰值；Ma=0.85和0.94时外壁面都存在明显的激波。

溢流阻力是进气道设计关注的重要性能，其定义是按照流量系数为1时溢流阻力为0，其他流量系数下的阻力增量即为溢流阻力。这就表示流量系数为1时的阻力系数是一个重要的参考量，其预测精度对进气道设计也有重要意义。文献[10,13-14]给出了溢流阻力的计算方法，但对于阻力系数绝对值的计算效果并未验证。在本文的计算中采用推阻分解方法，

利用式(4)可以获得进气道阻力，结果如图6所示，图上给出了不同马赫数下的进气道阻力系数与试验的对比，其参考面积为进气道的外罩最大截面积。从计算结果可以看出，采用本文的推阻分解计算方法，不仅能够准确预测进气道随流量系数变化的溢流阻力，其进气道阻力系数的绝对值也与试验符合良好。

2.2 DSFR喷管验证算例

喷管性能是机体/推进系统集成所关注的另一重要方面，着重关注喷管在地面状态下不同总压的推力系数，获得推力系统随总压的变化曲线，在飞行状态下需要利用该性能曲线进行推力与阻力的分解。因此喷管性能曲线的计算精度对于飞行推力的预测精度有直接的影响。AIAA自2011年起组织了三届PAW研讨会，旨在探讨CFD方法对于推阻分解的计算精度。第二届和第三届的喷管算例是典型的高涵道比民用航空发动机DSFR喷管(Dual Separate Flow Reference Nozzle)[11-12]。本文为了验证和演示推阻分解方法在喷管性能的计算过程，采用轴对称的高涵道比喷管进行CFD验证。

图7显示了喷管算例的模型、边界条件与计算网格，其中坐标的单位为英寸，与原始算例一致。喷管入口采用总温、总压边界条件，远场上游采用速度进口边界条件，下游采用无反射边界条件，壁面采用绝热固壁条件。为了更真实地模拟发动机试车台的静止外流条件，但同时也避免CFD的计算稳定性问题，外流需要采用一个极低速度的来流条件。该算例中外涵道总压始终为内涵道总压的1.2倍，内、外涵道总温均为环境温度的1.019倍。计算采用三套不同的计算网格测试网格敏感性，研究网格密度对于计算结果的影响，网格点数分别为87 500、172 000、345 000，不同网格之间的加密方式为x和y方向各加密1.4倍，这种加密方式与AIAA所举办的阻力预测研讨会(DPW)所推荐的网格加密方式[18]相似。

图7显示了计算所采用的稀网格，网格在喷管入口进行了适当加密。采用轴对称方式计算，圆周方向采用1个网格单元。为了保持x、y、z三个方向网格的密度匹配，从稀网格、中网格到密网格的轴对称计算扇形角度分别为4°、3°、2°。空间离散采用Roe迎风格式，湍流模式采用SST模式。

图8显示了不同压比下的流线分布和马赫数云图，这是外流马赫数为0.01时的密网格计算结果。从流线看，射流对于外流有明显的引射作用，外场流线向射流核心区集中。当外涵道总压低于1.89时，整个流道速度低于声速；当压比高于1.89时，流场出现超声速区域，并出现激波。

前文已经分析过，推阻分解中喷管性能系数是评价推力损失的重要参数，需要利用地面状态的性能参数评估飞行状态的推力损失，因此其计算精度对结果影响十分重要。波音公司的Wright[19]的误差估计显示，对于速度系数为0.99的喷管，其速度系数0.001的误差就将引起飞机全机1 count(即阻力系数0.0001)的阻力系数误差。

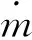
(11)

(12)

稀网格的风扇喷管流量系数稍有差别，其余结果具有很好的网格收敛性。计算网格引起的速度系数的误差小于0.0005。从计算结果看，中等网格计算结果和密网格计算结果几乎完全一致，由于密网格计算资源消耗较大，所以选择中等网格密度作为喷管性能分析的参考。

在等熵流动假设下，压比1.89时喉道就达到声速，出现堵塞，但由于边界层的作用，真实喷管达到堵塞的压比更高。图9显示当风扇喷管的压比达到约2.2时才趋于堵塞，此时流量系数和速度系数均较高，所以是典型民用航空发动机的典型设计状态。

在发动机地面试验中，通过测试设备将短舱外罩速度近似给定为0，但是在可压缩CFD分析中，大范围速度为0的计算域带来计算鲁棒性问题，所以需要在外场区域设定一个较小的流动速度。但外流流动会给短舱外罩带来阻力，从而使推力损失增加，速度系数降低。下面测试外场速度对计算精度和数值稳定性的影响。

图10给出了外场马赫数为Ma∞=0.01、0.02和0.05时中等网格的流量系数和速度系数与试验结果的对比。可以看出，在这个马赫数范围内，核心喷管和风扇喷管的流量系数变化很小，尤其是核心喷管，流量系数几乎不受外流速度的影响。从流量系数对比结果看，核心喷管的误差最大达到1%，但由于核心喷管流量很小，其误差权重也相对较小；风扇喷管的流量系数误差约为0.2%，与试验吻合较好。不同外流马赫数结果显示，速度系数明显受到外流速度的影响，这是由于外部流动在短舱外罩上造成的损失所致。结果显示，计算和试验的速度系数的变化趋势非

图9不同网格的流量系数和速度系数与试验对比
Fig.9Comparisonsofdischargecoefficientsandvelocitycoefficient

图10不同外流速度下的流量系数和速度系数与试验结果对比
Fig.10Comparisonsofdischargecoefficientsandvelocitycoefficientofdifferentexternalflowspeeds

常一致，这表明流动现象被准确捕捉。Ma∞=0.01、0.02和0.05的计算结果表明，外流速度越小，速度系数越大，当速度趋于0时趋于一个收敛的值。在真实发动机分析时往往需要根据不同外流速度下的速度系数外插出速度为0时的值。在本文计算结果中，不同速度下的Cv差别大约为0.002，考虑试验的误差带，计算与试验值的误差大约0.003～0.004左右，并且显示为整体的系统误差，便于进行修正，所以整体来看计算与试验有较好的吻合。

2.3 NAL-AERO-02-01 TPS验证算例

针对机体/动力系统的集成问题，推力与阻力的分解既要分析进气道性能，又要准确模拟喷管特性。推阻分解过程需要有三个步骤：首先计算发动机短舱在地面状态的性能系数，然后再计算飞行状态下的气动性能，最后利用推阻分解方法对推力与阻力进行后处理。针对机体与动力短舱的干扰问题，需要先分析独立短舱在地面状态的性能特性，然后分析短舱/吊挂/机翼构型的性能，获得各构型在地面状态下由于干扰量所带来的推力损失，最后利用推阻分解方法获得推力和阻力。总的来说，推阻分解计算结果的精确程度受到两方面影响，一是标定状态的速度系数精度，二是飞行状态的全机阻力预测精度。

本节以一个轴对称TPS (Turbine Powered Simulator)短舱模型NAL-AERO-02-01模型[20]为例，演示利用推阻分解方法计算带动力短舱的气动力过程。为了与真实民用航空发动机的短舱更为接近，本文将原始模型进行了放大，使其基于短舱外罩的雷诺数达到1.5×107(原始模型为2.0×106)，与典型窄体客机的发动机的雷诺数相当，其余计算参数如马赫数、喷流总温总压等与文献[20]相同。

图11显示了TPS短舱的计算网格。进气道唇口处采用C型网格准确捕捉进气道的溢流流动，喷管网格进行加密以分辨高压流体的膨胀过程，壁面法向第一层网格的y+约为1，采用轴对称方法计算，二维截面网格总数为7.0×104。采用ROE格式和SA湍流模式进行CFD分析。

以跨声速Ma∞=0.801的流动状态为例分析推阻分解的过程。以远场温度、压力作为参考量，风扇喷管的无量纲总温、总压分别为1.251和2.049，核心机喷管的总温、总压分别为0.690和1.406，进气道的流量系数为0.497。计算参考面积选取短舱外罩的最大截面积。为了获得地面试车状态下的喷管性能参数，首先以来流马赫数0.005、0.01、0.02三个状态进行短舱净推力分析，按照式(8)进行速度系数计算，三个状态的速度系数分别为0.9887，0.9886和0.9884，其中来流马赫数0.005最为接近地面静止状态，采用外插方法确定此压比下的喷管速度系数为0.9888。然后计算Ma=0.801时的流场，采用流量自动调节的方式获得指定的流量系数。图12显示了来流马赫数为0.005和0.801时两个流场的对比。其中在模拟地面测试状态时为了排除进气道对参数标定的影响，在风扇面采用了壁面条件。从图12可以看出，两个状态的喷管流场非常相似，但由于外流速度不同，喷流对外部流体的卷吸现象差别较大，导致外场流线差别较大。

图13给出了Ma=0.801状态下的压力分布计算与文献[20]试验值的对比，其中横坐标为相对坐标，C为短舱外罩的长度。虽然本文的计算雷诺数更大，但压力分布与试验也符合较好。

表1给出了根据CFD计算和推阻分解方法获得的计算结果。表1中进气道和喷管的流量以及各控制面的受力均基于CFD直接积分获得，推力和阻力采用推阻分解的方法获得。其中推力采用式(9)计算，当Cv=1时为理想推力，当Cv=0.9888即为扣除内阻损失后的实际推力。短舱所受合力与理想推力的差量即为短舱所受的总阻力。

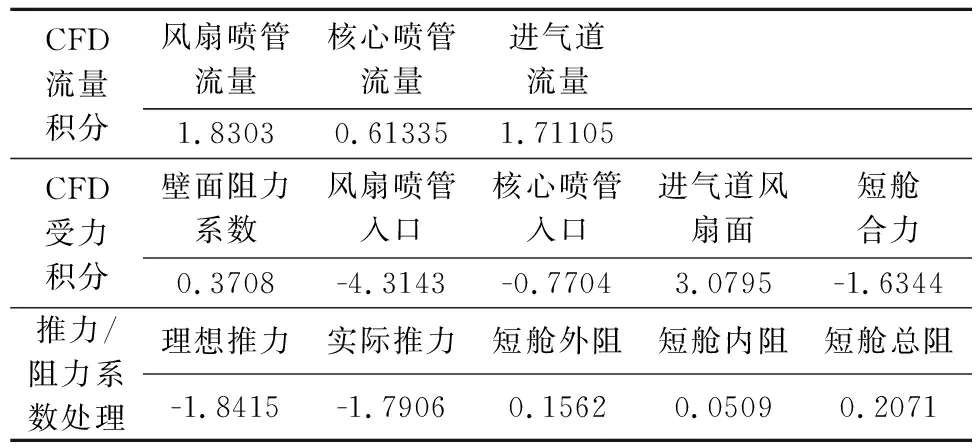
表1 Ma=0.801时推阻积分各受力分量分解(无量纲)Table 1 Thrust and drag components of Ma=0.801 case (non-dimensional)

当需要进行不同状态下的推阻分解分析时，若喷管的总温、总压没有发生变化，则可以用同样的速度系数计算推力，倘若喷管状态发生变化，就需要重新标定该压比下的地面试车状态的性能。表2给出了几个不同状态下的推阻分解结果，其中前5个状态是固定喷管流动状态、改变来流速度，最后1个状态改变了喷管流动状态。

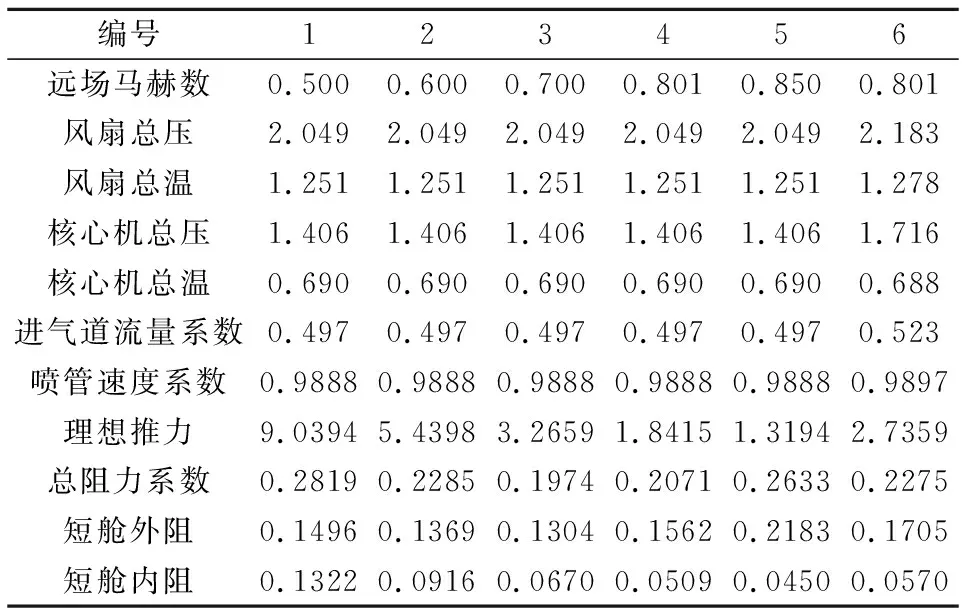
表2 不同计算状态下的短舱推阻分解结果(无量纲)Table 2 Thrust/drag bookkeeping results of different flow conditions (non-dimensional)

从变马赫数的结果可以看出，由于以来流速度作为参考值，因此无量纲的发动机理想推力随来流速度减小越来越大，相应的短舱内阻也越来越大。而进行推阻分解后的短舱外阻随马赫数增加先减小后增加。从图14的不同马赫数下的压力分布对比可以看出，在马赫数较小时没有激波，并且前缘吸力峰值较低；当马赫数逐渐提高，短舱前缘的吸力峰值提高，因此能够产生一定的推力分量，使短舱外阻减小；当马赫数继续增加，短舱外罩出现激波，并且激波逐渐增强，所以短舱外阻增加。

表2的最后一个状态是改变喷管流动状态的结果，此时需要重新标定喷管性能参数用于推阻分解分析。其中状态6与状态4相比发动机推力增大，喷流与外流之间的干扰增大，所以短舱外阻有所增大。

3 总 结

本文介绍了一种基于CFD的推阻分解方法，可用于带动力短舱计算时的推阻分解。推阻分解方法广泛应用于飞机公司与发动机公司，其主要原理是采用流体力学的控制体理论，针对推力和阻力产生的各自区域进行受力分解，然后利用风洞测试或者CFD分析确定各项阻力分量。

本文首先分析了推阻分解方法的控制体理论，明确各项推力与阻力分量的计算方法。然后采用三个算例对计算方法进行详细分析。其中进气道算例用于验证推阻分解方法对于溢流阻力的计算效果；喷管算例用于验证和分析速度系数和流量系数的计算精度；最后是一个完整的TPS短舱分析，用于演示推阻分解方法对于动力短舱阻力分量的计算过程。三个不同算例的结果表明，本文CFD计算结果与试验有较好的吻合，并且推阻分解过程能够准确分辨推力与阻力分量。

参 考 文 献：

[1]Rooney E C. Thrust and drag: Its prediction and verification, Chapter 2, Thrust-Drag Accounting Methodology[M]//Covert E E, edited. Progress in Astronautics and Aeronautics, vol. 98. American Institute of Aeronautics and Astronautics, 1985.

[2]SAE Technical Standards. In-flight thrust determination, appendix c thrust and drag accounting, and appendix e case studies and applications[R]. SAE Aerospace Information Report AIR1703 rev. A, 2012.

[3]MIDAP Study Group. Guide to in-flight thrust measurement of turbojets and fan engines, Chapter 2 Propulsion system thrust and drag bookkeeping[R].Advisory Group for Aerospace Research and Development. AGARD-AG-237, 1979: 27-62.

[4]VonGeyr H F, Rossow C C. A correct thrust determination method for turbine powered simulators in-wind tunnel testing[R]. AIAA 2005-3707.

[5]Hunt D N. Experimental techniques used to evaluate propulsion system interference effects on the cruise configuration of the boeing C-14[R]. AIAA 1979-0335, 1979.

[6]Dusa D, Lahti D J, Berry D. Investigation of subsonic nacelle performance improvement concept[R]. AIAA 1982-1042, 1982.

[7]Bousquet J M. Survey of engine integration testing in ONERA wind tunnels[R]. AIAA 2005-3705, 2005.

[8]Winkler C M, Dorgan A J. BCFD analysis for the 1st AIAA propulsion workshop: Nozzle results[R]. AIAA 2013-3731.

[9]Zhang Y F, Chen H X, Zhang M, et al. Performance prediction of conical nozzle using Navier-Stokes computation[J]. Journal of Propulsion and Power, 2015; 31(1): 192-203.

[10]Spotts N, Guzik S, Gao X F. A CFD analysis of compressible flow through convergent-conical nozzles[R]. AIAA 2013-3734.

[11]Mikkelsen K L, Myren D J, Dahl D G, et al. Initial subscale performance measurements of the AIAA dual separate flow reference (DSFR) Nozzle[R]. AIAA 2015-3883.

[12]Li Z, Chen H X, Zhang Y F. NSAWET results of the dual separate flow reference nozzle from AIAA PAW02[R]. AIAA 2015-3779.

[13]张美红, 张冬云, 王美黎, 等. 基于CFD和推阻分解技术的全机溢流阻力预测与分析[J]. 空气动力学学报, 2016, 34(5): 625-630.

[14]张兆, 陶洋, 黄国川. 发动机短舱溢流阻力的数值模拟[J]. 航空学报, 2013, 34(3): 547-553.

[15]Baals D D, Smith N F, Wright J B. The development and application of high-critical-speed nose inlets[R]. Langley Aeronautical Laboratory National Advisory Committee for Aeronautics, NACA TR-920, 1948.

[16]Richard J R. An investigation of several NACA 1-series axisymmetric inlets at Mach numbers from 0.4 to 1.29[R]. NASA TM X-2917, 1974.

[17]Richard J R, William K A. A wind tunnel investigation of three NACA 1-series inlets at Mach numbers up to 0.92[R]. NASA TM-110300, 1996.

[18]Mavriplis D J, Vassberg J C, Tinoco E N, et al. Grid quality and resolution issues from the drag prediction workshop series[R]. AIAA 2008-930.

[19]Wright F L. Comparison of least squares curve fit and individual sample statistical analysis results of calibration data for the velocity coefficient of a flow nacelle[R]. AIAA 1994-2587, 1994.

[20]Hirose N, Asai K, Ikawa K. Transonic 3-D Euler analysis of flows around fanjet engine and TPS (Turbine Powered Simulator), comparison with wind tunnel experiment, evaluation of TPS testing method and 3-D flow[R]. National Aerospace Laboratory, TR-1045, 1989.