Spar式风机基础在风浪联合作用下运动响应研究

蒙宣伊，刘永清

(湘电风能有限公司，湖南 湘潭 411100)

1 概述

海上风能是一种被广泛认可、可开发利用的可再生能源，能够满足当今能源增长需求，从而提高全球能源供应安全性。相比其它存在于海洋中的可再生能源，比如波浪能、潮汐能，风能的开发技术最为成熟。最近10年，海上风电发展十分迅速，目前大部分开发的风电场的水深最多为40～50 m，因此，大部分采用的基础是固定式基础，比如单桩、导管架、重力式、三脚架和多桩等形式。然而，当水深超过60 m时，从成本上考虑，漂浮式风机基础将会是更好的选择。漂浮式风机基础主要分为三种：半潜式、张力式和Spar式。

在基础的设计时，对其运动性能的评估是非常重要的。对于漂浮式结构来说，升沉、纵摇和垂荡的影响是最大的。因此，通过仿真计算得到海上风机典型工况下运动的时历曲线，可以为基础的设计工作提供参考。

最近几十年，有大量学者对Spar式风机基础进行了研究，有的学者从风电场的技术和经济方面进行概念设计。Nielsen等采用数值仿真和试验方法进行了Spar基础的整体动力性能研究，并将结果进行了对比。Matsukuma和Utsunimiya基于多体动力学方法研究了在某一特定风速下考虑叶轮转速对漂浮式基础的运动响应的影响。Jonkman等采用对固定式和漂浮式基础的结构动态响应进行了验证。Karimirad和Moan基于气动－水动弹性理论，采用时域的方法研究了Spar基础在极限工况下的运动响应情况。Bagbanci H等对Spar和半潜式基础分别采用长期预报的方法进行分析，研究它们的水动力性能。

在本研究中，采用水动力专业软件AQWA(Advanced Quantitative Wave Analysis)对Spar基础进行水动力分析。首先，采用频域方法，得到其升沉、纵摇和纵荡等运动响应。其次，对基础的锚泊系统进行建模，基于时域方法，计算基础结构在三种典型工况下运动的时历曲线。最后，基于统计方法，得到各工况下运动响应的统计值。

1 Spar基础和整机系统模型

Spar基础整机系统包含：Spar式基础、塔筒、机舱和叶轮。图1为基础和锚泊系统的示意图。在本文的研究中，机舱和叶轮是以质量点进行替代的。风推力则假定为作用在轮毂中心处的恒定力，即相对平均海平面90 m处。整个基础吃水为120 m，底部直径为9.4 m，高度－12～4 m处为过渡段，上部直径为6.5 m。塔筒采用锥形变截面，底部直径为6 m。基础与塔筒的交界面位于海平面上15 m处。锚泊系统由3根互成120°角的锚链组成，锚泊点位于水线面以下70 m处。叶轮重量和分布采用美国国家可再生能源实验室(National Renewable Energy Laboratory，NREL)5 MW风机模型，基础和风机模型参数见表1，系统重心的坐标为(0，0，－62.82 m)，锚泊系统的参数见表2。

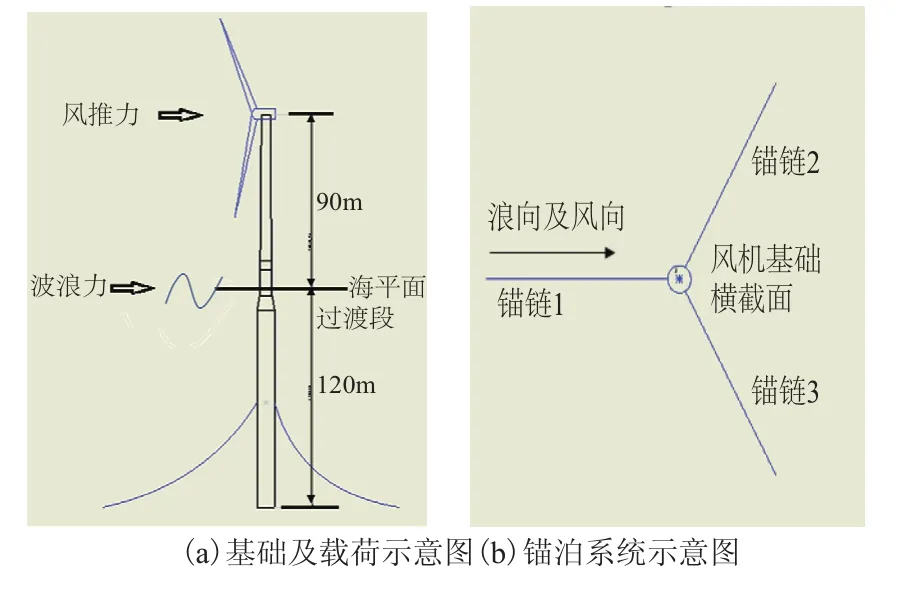
图1 Spar基础风机系统示意图

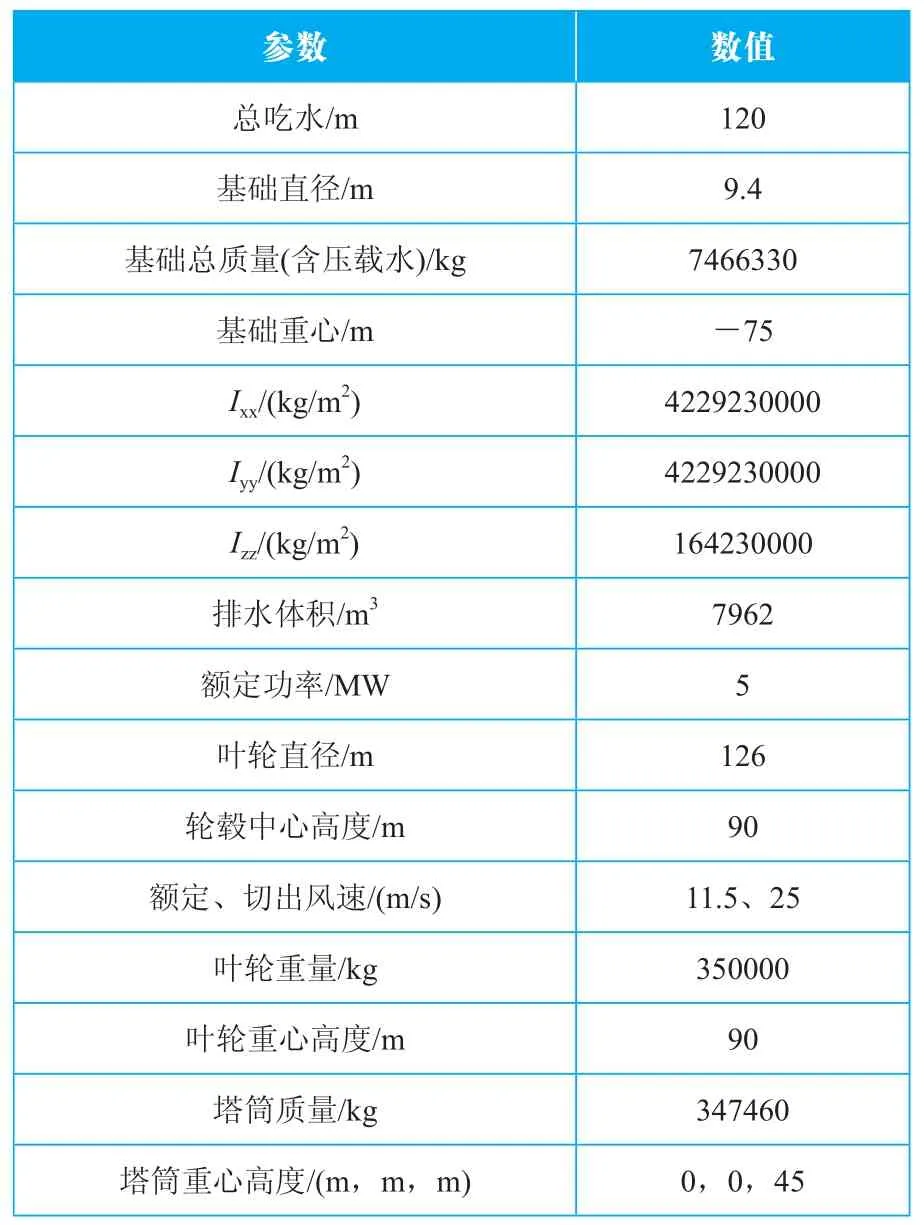
表1 风机和基础模型参数

表2 锚泊系统参数

2 Spar基础数值分析

2.1 频域分析

对于漂浮式基础来说，通过频域方法研究其6自由度运动响应是十分必要的。由于Spar基础的对称性，横摇运动特性与纵摇运动比较类似，横荡由于和波浪方向垂直而可以忽略，艏摇在分析时数值很小。因此，本文仅给出升沉、纵摇和纵荡等三个自由度的幅值响应函数(Response Amplitude Operators， RAOs)。波浪周期为3～30 s，间隔为1 s，运动响应见图2。

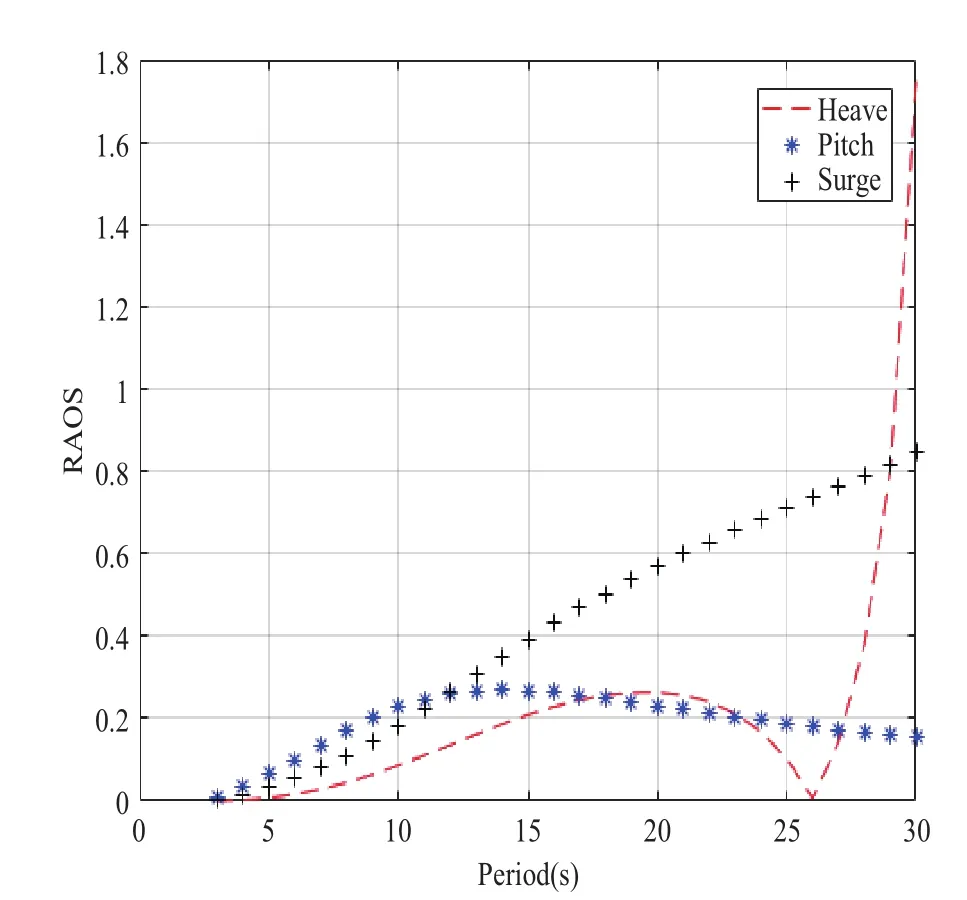
图2 Spar基础运动响应

从图2可以看出，基础结构的水动力性能比较优越。升沉的RAOs在周期为3～25 s内的值小于0.3，超过25 s后响应幅值迅速增加。纵摇的响应幅值的峰值对应的周期为14 s，但其响应幅值为0.26，表征纵摇性能比较优越。纵荡的响应幅值随着波浪周期增大而增大。风机额定转速为6.9～15 rpm，1P频率为0.115～0.2 Hz，3P频率为0.345～0.75 Hz，对应周期在10 s以内，因此，基础的性能满足要求。

2.2 工况设置

基础的时域仿真通过水动力软件AQWA完成，在仿真过程中考虑了风载对系统的运动响应的影响。根据风机运行状态，本文考虑三种典型工况，即额定风速(作业)工况、极限切出风速工况、极限生存风速工况，工况设置见表3。

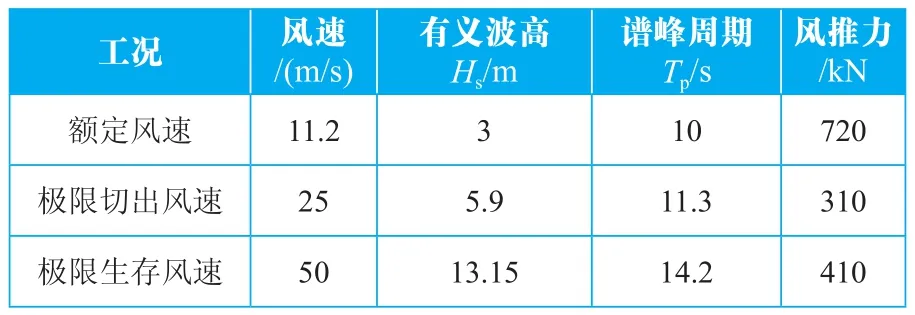
表3 风机典型工况设置

时域计算时，按照表3进行工况设置，仿真步长为1 s，总仿真时长为3600 s，计算所采用的波浪谱为Jonswap谱，其公式如下：

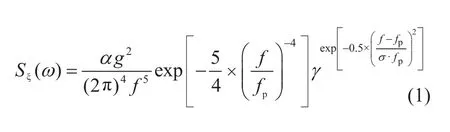
式中：α为无因次常数；g为重力加速度；γ为升高因子，取值范围为1～3.3；σ为峰形参数，若ω≤ωp则σ=0.07，若ω＞ωp则σ=0.09；f=1/Tw；fp=1/Tp；

在本文中仅仅考虑180°(见图1(b))且风浪同向时的情况，对于其它方向和风浪不同向的情况并没有进行考虑。

2.3 时域分析

2.3.1 额定风速工况

基础在额定风速工况下的升沉、纵摇、垂荡和各锚链拉力的时历响应曲线，详见图3～图5，图中蓝线表示基础仅考虑波浪作用下的响应曲线，而红线为基础在风浪联合作用下的响应曲线。从图3的红线可以看出，基础在风浪联合作用下产生了约0.55 m的向下初始偏移。从图4可以看出，由于风载，基础发生了2.5°的初始倾角，而且可以明显看出风浪联合作用下的运动响应幅值要比仅考虑波浪作用时的运动响应幅值大。从图5可以看出，基础在风载作用下产生了约8.78 m的纵向偏移。

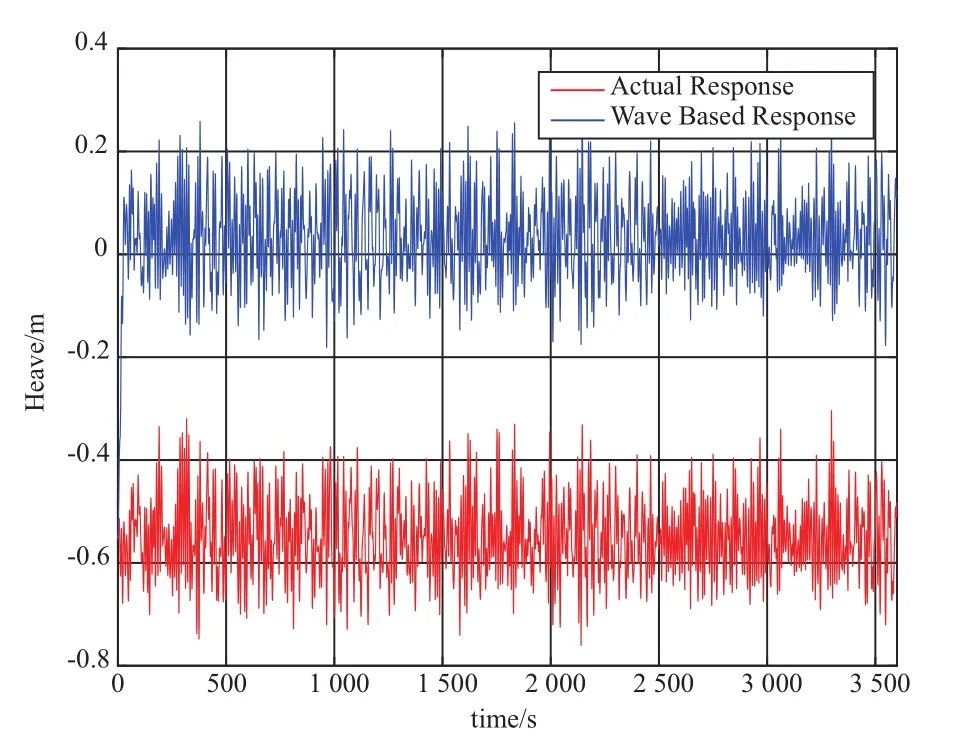
图3 额定风速工况下升沉时历曲线

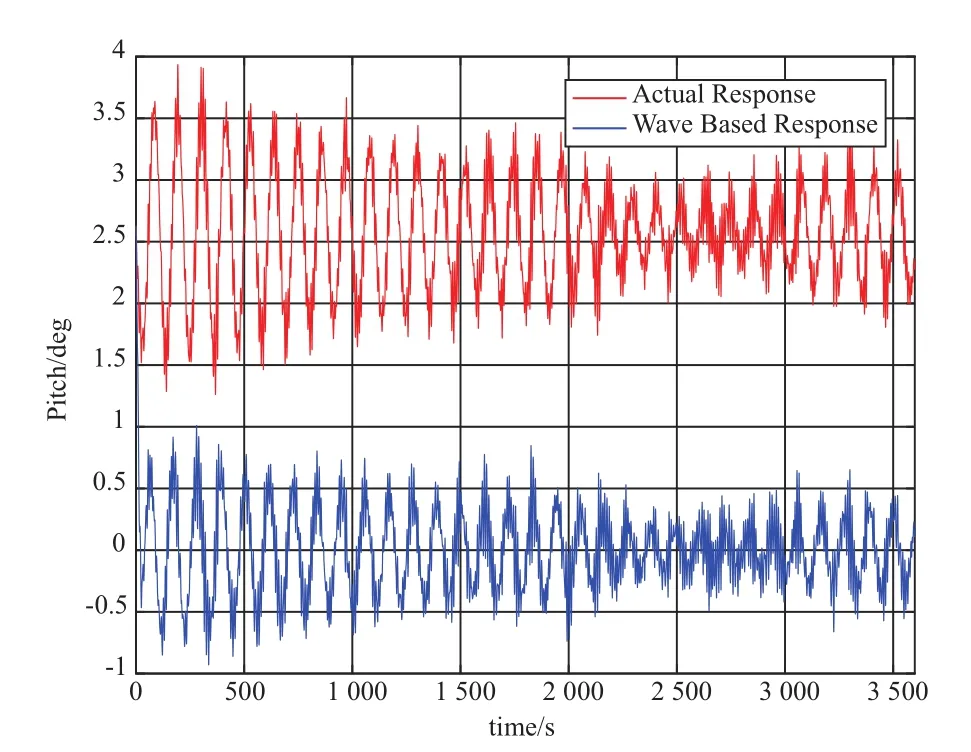
图4 额定风速工况下纵摇时历曲线

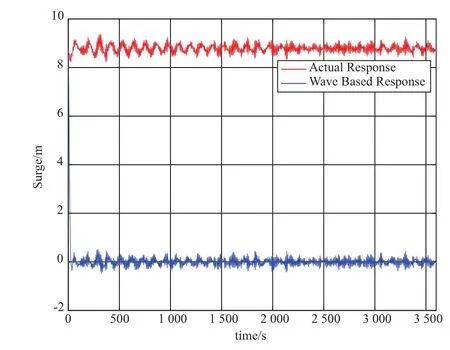
图5 额定风速工况下纵荡时历曲线

图6给出了三个不同方向的锚链所受拉力的时历曲线。基于锚链的分布以及风浪载荷的作用方向(见第1章图1)，锚链1所受的拉力要大于2号、3号锚链。从图6也可以看出，计算结果与实际情况比较吻合。2号、3号锚链的受力情况应该基本一致，因此，在本图中采用同一条曲线来表示。

2.3.2 极限切出风速工况

极限切出风速工况下的基础升沉、纵摇、纵荡和各锚链截面拉力的时历曲线，详见图7～图10。相比额定风速工况，极限切出风速工况下的升沉、纵摇均有所增加，而纵荡和锚链拉力由于风推力减少而减少。升沉最大幅值为0.8 m，最大纵摇为2°，最大倾角为3.8°。在极限切出风速工况下，风机在风浪作用下会产生4 m的初始纵荡。

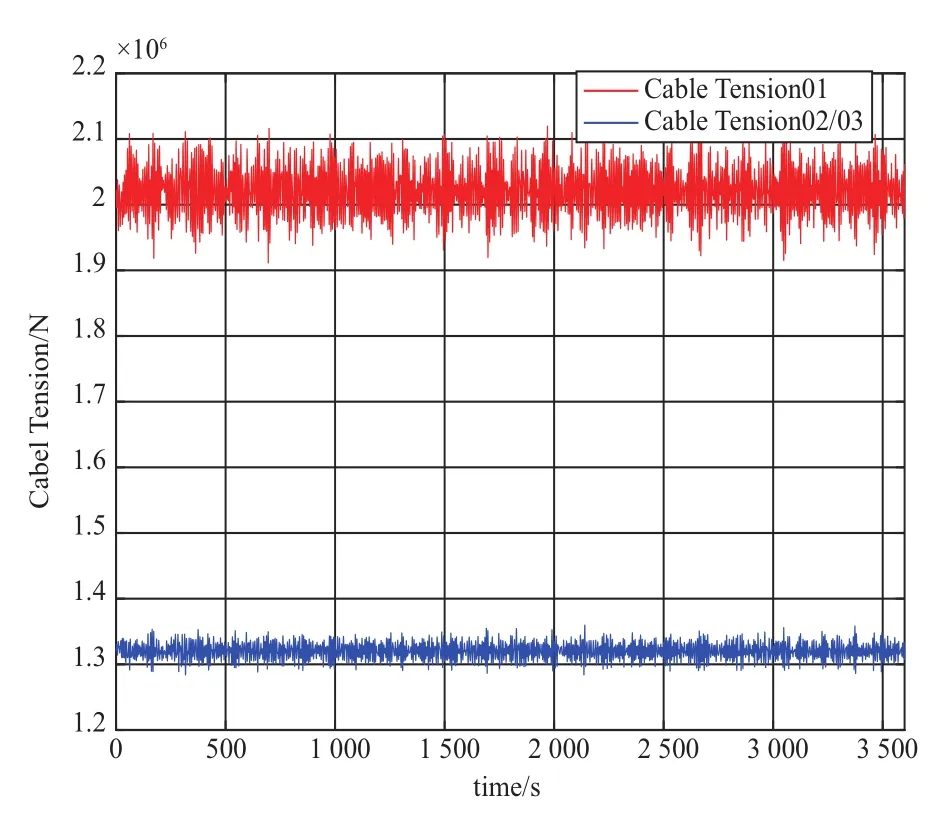
图6 额定风速工况下各锚链拉力时历曲线

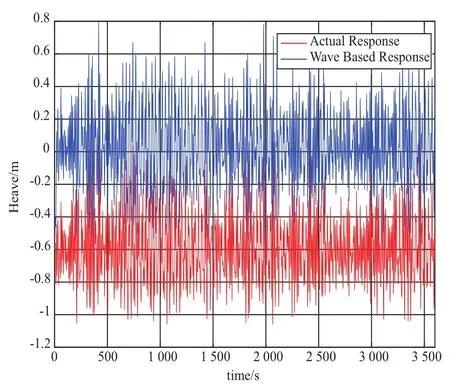
图7 极限切出风速工况下升沉时历曲线

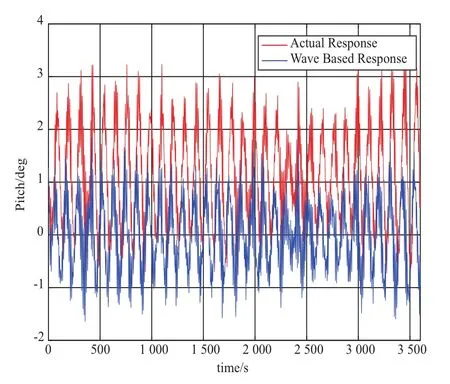
图8 极限切出风速工况下纵摇时历曲线

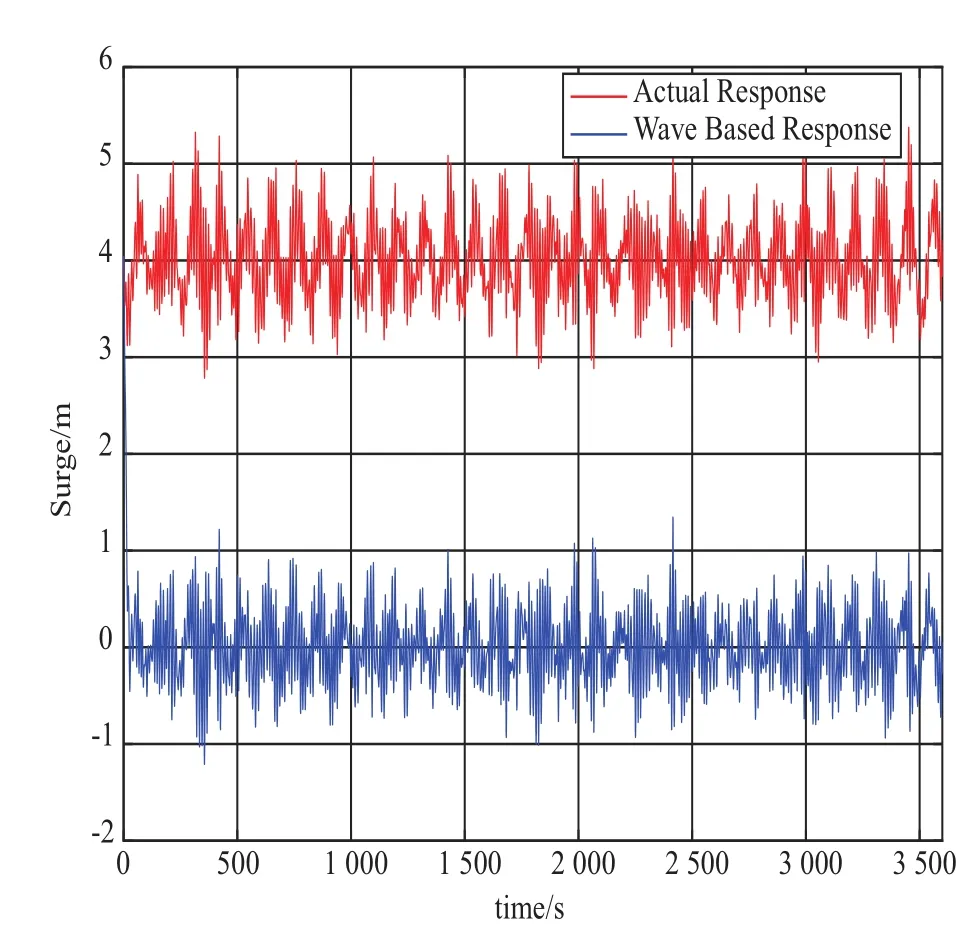
图9 极限切出风速工况下纵荡时历曲线

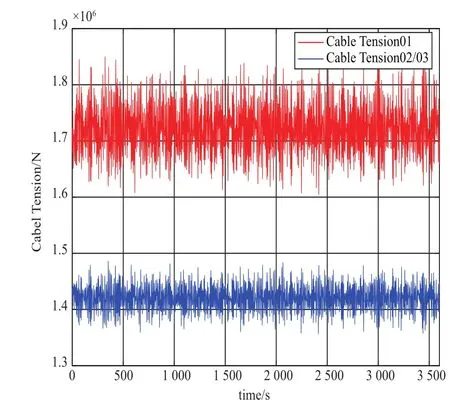
图10 极限切出风速工况下各锚链所受拉力时历曲线

2.3.3 极限生存风速工况

极限生存风速工况下的基础升沉、纵摇、纵荡和锚链截面拉力的时历曲线，详见图11～图14。在极限生存风速工况下，整个系统的升沉、纵摇、纵荡及锚链拉力增加比较明显。从图11可以看出，实际升沉响应要略小于仅仅由波浪产生的响应。从图12可以看出，最大倾角达到10°，幅值达到8°。

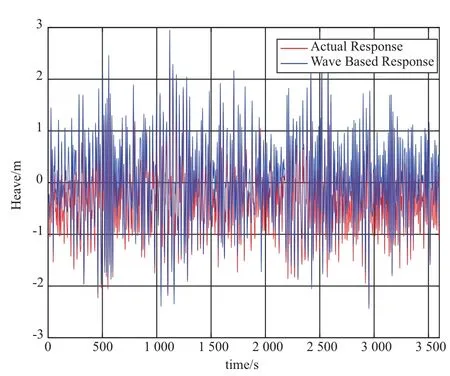
图11 极限生存工况下升沉时历曲线

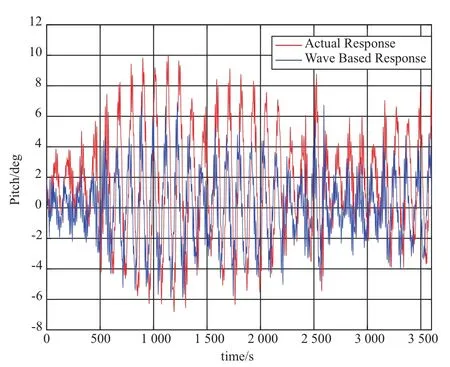
图12 极限生存风速工况下纵摇时历曲线

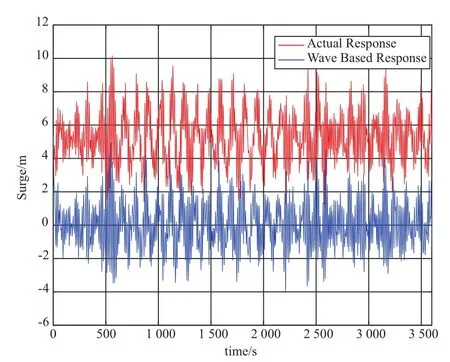
图13 极限生存风速工况下纵荡时历曲线

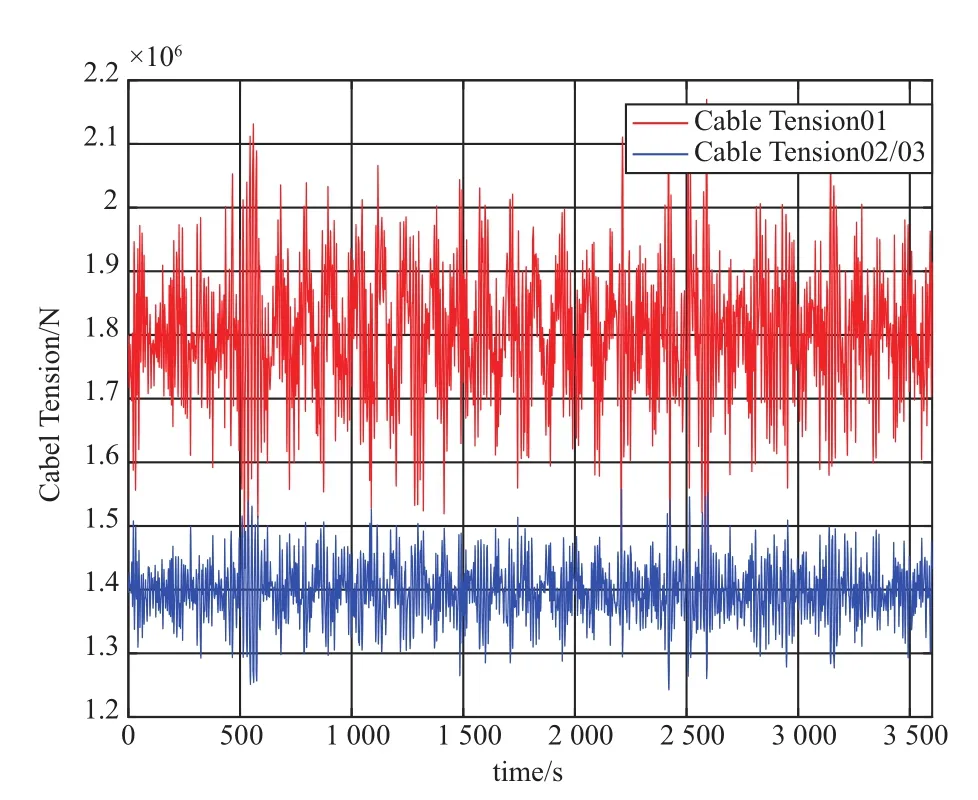
图14 极限生存风速工况下锚链截面拉力时历曲线

3 统计分析

基于统计学方法，对各运动响应的时历曲线进行统计分析，得到响应的均值、方差、最小值和最大值。表4～表6列出了额定风速、极限切出风速和极限生存风速工况下各响应的统计值，可以看出，随风速增加和海况变复杂，升沉、纵摇响应的均值、方差、最大值及最小值均增大。在极限生存风速工况下，纵摇最大倾角超过10°，接近整机系统最大安全值。纵荡和锚链拉力均值主要取决于风推力，但是极限生存风速工况方差最大，证明在该工况下波浪影响最大。

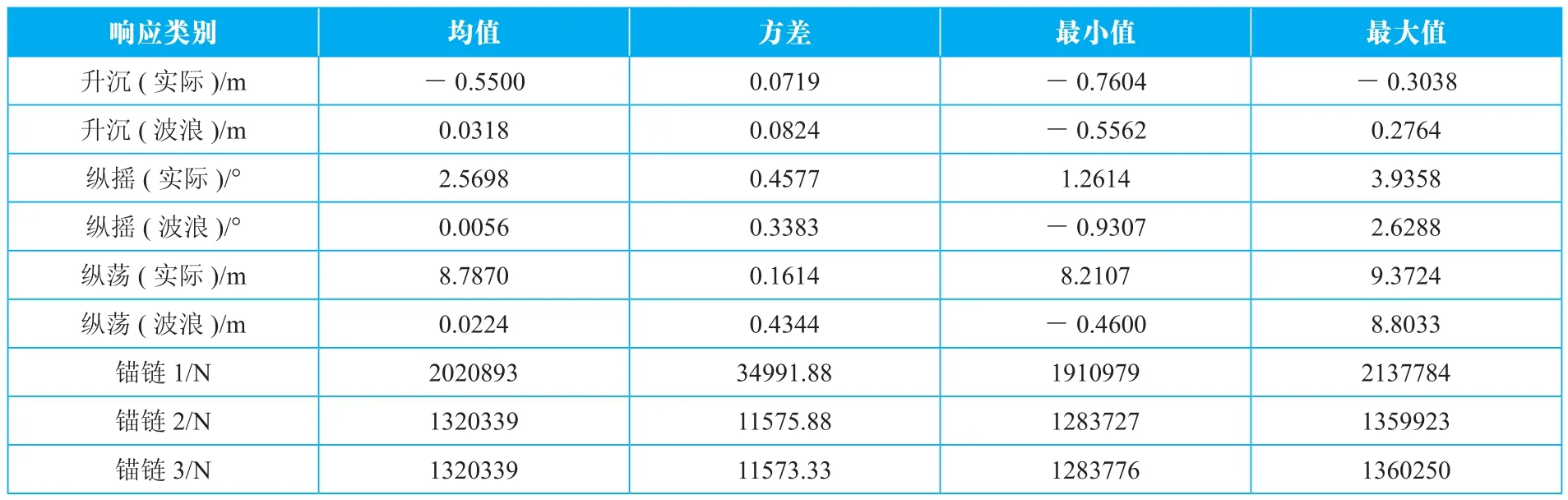
表4 额定风速工况下各响应统计值

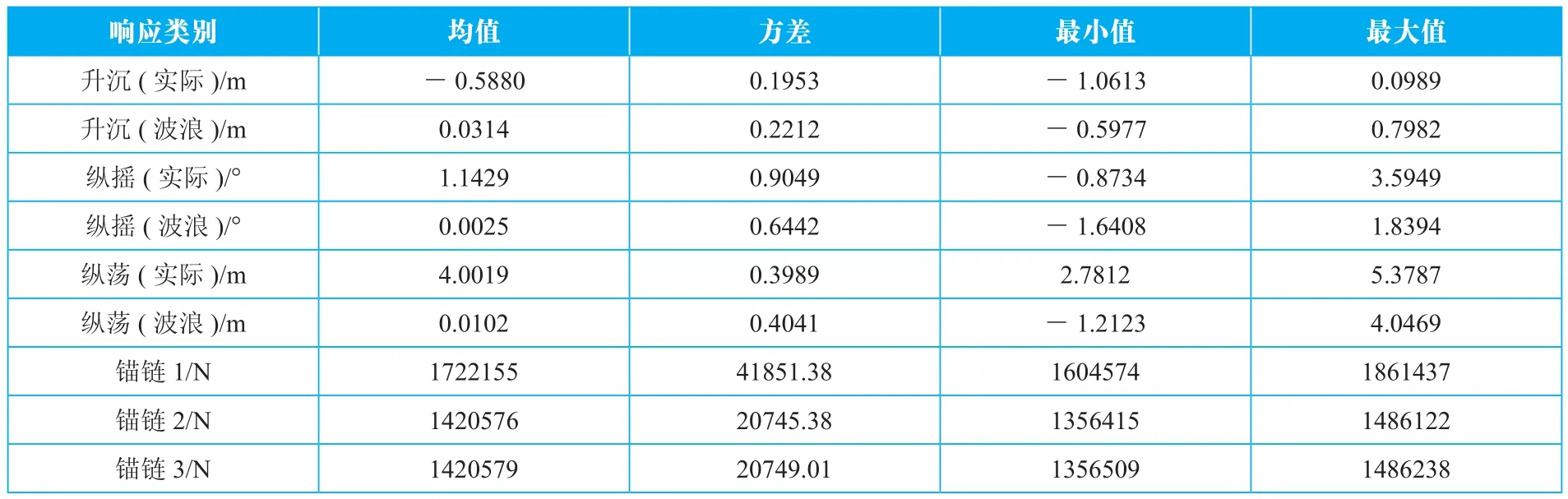
表5 极限切出风速工况下各响应统计值

表6 极限生存风速工况下各响应统计值

续表6

4 结语

本文基于三维水动力学软件AQWA对Spar式风机基础系统的水动力性能进行了研究。从频域的结果来看，该系统在风机运行风速范围内性能比较优越，ROAs值比较小，但在波浪周期较大时(＞20 s)响应迅速增大。

从时域方法的结果可以看出，风推力对基础系统的运动响应影响较大，如纵摇和纵荡在风推力作用下有一个明显的初始倾角或位移。锚泊系统中，1号锚链受力最大，由于对称性，2号、3号锚链的拉力时历曲线基本一致。

本风机基础系统在极限生存风速工况下的响应幅值最大。其中，升沉最大值为2.3 m左右，纵倾最大角度为10°，纵荡最大值为10 m，1号、2号、3号锚链的拉力均有显著增加。

从计算结果来看，Spar式基础的水动力性能比较优越。在额定风速工况下，纵摇和升沉比较小，满足风机发电要求。整机系统满足安全性要求，能够适应恶劣的极限生存风速工况。

[1]Karimirad M, Michailides C.V－shaped semisubmersible offshore wind turbine: An alternative concept for offshore wind technology[J].Renewable Energy，2015，83.

[2]Nielsen F G，Hansen T D，Skaare B.Integrated dynamic analysis of floating offshore wind turbines[C]// Proceedings of the ASME 2006 25th International Conference on Ocean，Offshore and Arctic Engineering.Hamburg，Germany：The American Society of Mechanical Engineers，2006：671－679.

[3]Hidekazu M，Tomoaki U.Motion analysis of a floating offshore wind turbine considering rotorrotation[J].The IES Journal Part A：Civil & Structural Engineering，2008，1(4).

[4]Jonkman J，Musial W.Offshore code comparison collaboration (OC3)for IEA wind task 23 offshore wind technology and deployment[R].Golden，Colorado，USA：National Renewable Energy Laboratory，2010.

[5]Karimirad M.，Moan T.Extreme structural dynamic response of a Spar type wind turbine[C]// ASME 2010 29th International Conference on Ocean，Offshore and Arctic Engineering，Paper No.OMAE2010－20044，Shanghai，China，2010.

[6]Bagbanci H，Karmakar D，Soares C G.Comparison of Spar and Semisubmersible floater concepts of offshore wind turbines using long－term analysis[J].Journal of Offshore Mechanics and Arctic Engineering，2015，137.

[7]Century Dynamics Ltd.ANSYS AQWA user manual v13.0[Z].Horsham，UK：2010.

[8]Muliawan M J，Karimirad M，Gao Z，et al.Extreme responses of a combined spar－type floating wind turbine and floating wave energy converter(STC)system with survival modes[J].Ocean Engineering，2013，65(2).

[9]DNV－OS－J101－2014.Design of offshore wind turbine structures[S].