VISDMiner:一个交互式数据挖掘过程可视化系统
王永胜,李 晖,陈 梅,戴震宇,朱 明
(1.贵州大学计算机科学与技术学院,贵州 贵阳 550025; 2.贵州省先进计算与医疗信息服务工程实验室,贵州 贵阳 550025; 3.中国科学院国家天文台,北京 100012)
0 引 言
数据挖掘技术被广泛用于从大量的、不完全的、模糊的、随机的原始数据中提取出潜在有用、可信、新颖的信息和知识[1]。但是由于数据挖掘技术本身的复杂性,一般用户很难理解其挖掘工作的流程,得到的挖掘结果往往不够直观,这增加了挖掘结果评估和解释的难度。要解决上述问题,以便从数据中挖掘出更多的有价值的数据信息并以生动直观的形式呈现给用户,如果仅采用传统的数据挖掘技术进行解决,用户没有交互参与其中根据自己的领域知识和经验去监督算法的执行,则容易得到复杂模糊的信息甚至错误的信息,造成信息的不易理解和结果正确率低的问题[2-3]。针对目前数据挖掘过程中存在的问题,本文将可视化技术与数据挖掘技术结合在一起进行探索研究,设计并实现一个面向高维数据集的交互式数据挖掘过程可视化系统VISDMiner。传统的数据挖掘是以算法为中心的,直接产生结果集,中间执行过程用户不可知,在数据挖掘过程中通常没有引入用户的参与和交互,数据挖掘过程不透明且难于理解、挖掘结果复杂难懂等问题接踵而至[4]。本文设计并实现的VISDMiner系统在挖掘过程中,以用户交互为中心,让用户可以基于自己的领域知识和经验,根据数据挖掘过程中各个部分产生的可视化子结果集来设置和调整算法模型与可视化参数,以此促进用户根据观察挖掘出来的信息做出相应的判断、纠正等引导操作,并提高整个数据挖掘过程的灵活性、交互性以及准确性[5]。
目前,复杂高维数据的挖掘分析和可视化展示仍存在一定的难度[6-7]。本文设计并实现的VISDMiner系统在处理高维数据集时,首先采用本文提出的改进的特征选择算法MIC-PCA进行数据预处理,然后结合可视化技术对数据统计分析和数据挖掘的执行过程进行分析处理。VISDMiner系统以数据挖掘技术和可视化技术做支撑,将数据挖掘的中间各个环节以及数据本身的一些抽象信息和数据间潜在的联系用简明直观的形式展示给用户,帮助用户更深入地了解数据挖掘的执行过程并进而探索数据的趋势和有价值信息。
1 数据挖掘过程可视化
数据挖掘过程可视化是将可视化技术融入到数据挖掘过程中,数据挖掘过程可视化一般是将数据挖掘算法的参数和影响因子作为可视化对象进行分析[8]。传统的数据可视化一般只是将数据对象作为研究对象,具体的数据挖掘算法过程本身并没有进行有效的可视化展示,可视化技术与数据挖掘算法之间的结合是松散的[9-10]。VISDMiner系统的主要思想就是面对高维数据集基于特征选择技术实现数据挖掘过程可视化,并且在数据挖掘过程中让用户参与其中,用户根据数据挖掘过程可视化的中间结果集,基于领域知识和经验通过调整算法模型参数和可视化参数,并直接观察到其对计算结果的影响进而改进数据挖掘结果。
数据挖掘过程可视化的工作流程如图1所示。

图1 数据挖掘过程可视化流程图
数据挖掘过程可视化的具体流程简述如下:
1)分析数据挖掘算法。对数据挖掘算法进行分析,确定可视化参数,并分离出数据挖掘算法的中间结果和参数,将其作为可视化对象进行进一步分析。
2)选择可视化模型。选择合适的可视化展示模型对数据挖掘各个阶段产生的中间结果集进行可视化展示。
3)数据挖掘过程可视化。用户针对算法参数或者可视化参数进行交互,并基于可视化中间结果集的可视化和分析来决定下一步探索操作。
2 系统总体设计
VISDMiner系统的总体结构如图2所示。主要包括可视化表现层(表示层)、执行引擎服务层(服务层)和数据层3个部分。

图2 VISDMiner系统的总体结构图
图2中执行引擎服务层主要负责对数据的分析处理和数据挖掘过程的可视化展示。具体可分为数据预处理模块、可视化数据挖掘引擎模块以及数据挖掘结果模型评估模块。
1)数据预处理模块。该模块采用MIC-PCA特征选择方法对高维数据进行降维处理。MIC-PCA是本文提出的一种改进的主成分分析算法,在本文的第3章将详细介绍该算法及其实验效果。
2)可视化数据挖掘引擎模块。该模块构造数据挖掘算法模型、提取算法参数和可视化参数、设置阈值等,并允许用户一定程度地参与到数据挖掘的交互式分析过程中。数据挖掘过程中产生的中间结果集会以特定的可视化形式展示给用户,作为决定下一步分析探索操作的支撑信息。
3)数据挖掘结果模型评估模块。对数据挖掘过程中产生的中间结果集进行不同形式的可视化展示,让用户根据其性能指标对算法参数和可视化参数作进一步的调整。
3 MIC-PCA算法
3.1 MIC-PCA算法设计思路
针对传统PCA算法定义相关性矩阵只考虑变量间线性关系,以及降维过程忽略类别信息造成分类准确率下降的不足之处,本文提出一种基于最大信息系数的主成分分析算法MIC-PCA以用于特征选择。该算法从计算变量间最大信息系数的角度出发来确定变量间的依赖程度进而选择主成分。这种方法可以提供更多特征间以及特征与类别关系的信息,采用该方法在进行特征选择时降维效果更好。在降到同样特征维数下,其分类准确率更高。
由主成分分析算法的原理可知,传统PCA降维的主要思想是通过衡量2个变量间的相关性,去掉冗余特征,利用线性组合用维数较少且不损失数据太多信息的“新特征”代替原来的数据作为新的主成分[11-12]。根据数理统计的观点,主成分的方差越大,说明它包含的信息越多,表明该主成分越重要[13]。求方差最大化可以转化为求协方差的特征值和特征向量,根据方差最大化要求,目标可转化函数为:
AT∑A=Λ
(1)
其中,A是协方差矩阵Σ的特征向量为列组成的矩阵,Λ是由协方差矩阵Σ特征值组成的对角矩阵,在主成分分析中主成分个数k是由这k个主成分对应的特征值之和所占总体特征值之和的比重来确定,称累计贡献率[14]。
2011年Reshef[15]等人提出了一种基于信息论的度量标准——最大信息系数(Maximal Information Coefficient, MIC)。最大信息系数主要用于衡量2个变量间互相依赖程度的强弱,不仅可以度量变量间线性、非线性的依赖关系,还可以对一些非函数依赖关系进行度量。最大信息系数的本质就是利用互信息和网格划分方法进行计算。互信息是一种有效的信息度量方法,常用于度量样本间的相关性,可以看成是一个随机变量中包含另一个随机变量的相关信息量[16]。给定2个随机变量x和y,若它们各自的边缘概率分布和联合概率分布分别为p(x)、p(y)和p(x,y),则它们的互信息定义为:
(2)
将一个数据集D划分为x列y行的网格,计算划分网格G中的每个单元的概率。其中,概率值=单元中的点数/总点数,数据集D在网格上的互信息为I(x,y)。可知,在同一个数据集上可以有很多种网格划分方法,每一种划分都会得到不同的互信息值,定义划分网格G下样本数据集D的最大互信息的公式为:
I*(D,x,y) = max I (D|G)
(3)
其中,D|G表示数据集D进行G网格划分,最大信息系数主要利用互信息衡量网格划分的好坏,不同网格划分下得到一个最大互信息值组成特征矩阵,该特征矩阵定义为M(D)x,y,有:
(4)
最大信息系数定义为:
(5)
其中,n为样本大小,B(n)为网格划分x×y的上限值。MIC是一种归一化的互信息,当2个变量的最大信息系数越小时,说明2个变量之间所包含的相同信息也越少;当2个变量的最大信息系数越大时,说明2个变量之间所包含的相同信息也越多。
本文提出一种基于最大信息系数的主成分分析特征选择算法MIC-PCA。该算法在进行计算时引入类别信息,并选择用各个类别条件下特征间的最大信息系数矩阵之和而不是传统PCA算法中的协方差矩阵进行降维计算。具体改进过程如下:
将式(1)改为:
BΤφWB=Λ
(6)
其中,φW表示各个类别条件下特征之间最大信息系数矩阵之和,B为MIC-PCA的转换矩阵,其列向量βk为φW的特征向量,Λ为φW对角线元素是特征值的对角阵。
(7)
其中,m表示样本类别总数,MIC(W|C)表示在类别C条件下特征W两两之间的最大信息系数矩阵。MIC(W|C)的第i行第j列元素为MIC(wi;wj|C),表示类别C条件下特征wi和wj之间的最大信息系数。
MIC-PCA的主成分为f,则有:
f=BTx
(8)
第k维主成分fk=βkTx,βk是主成分fk的转换系数,简称主成分的系数。

(9)
其中n为总数,u为最大信息系数矩阵的特征值,选择累计贡献率为85%~95%的前m个主成分作为新的特征。
MIC-PCA算法的伪代码见算法1。第一步(line 1),使用最大信息系数(MIC)处理数据集,得到最大信息系数MIC;第二步(line 2),将最大信息系数与PCA结合,得到数据集的特征值与特征向量,即该数据集的特征空间;第三步(line 3)设置阈值;最后(line 4),得到降维后数据特征。
算法1ALGORITHM MIC-PCA
ALGORITHM MIC-PCA(S, D, C, N)
Input: multi-dimension dataset S, dimension D, class C, the number of data N
Output: the accuracy of the result for classify A, reduction-dimension RD
1.MIC=MIC(S, D, C, N) //measure the MIC for inner-demension and demension-class
2.(eigvalue,eigvector)=MIC //call for the PCA, including in the parameter max information corrlation
3.Set the threshold//select features
4.Get principal component
3.2 MIC-PCA性能分析
3.2.1 实验数据及设置
为了验证MIC-PCA算法的降维效果和分类性能,选取UCI机器学习库中的3个标准数据集对算法进行验证(见表1)。在实验中采用随机抽样的方法对各个数据集进行实验,验证2种特征选择方法分类准确率采用的分类方法分别是k近邻算法(KNN)、支持向量机算法(SVM)和朴素贝叶斯算法(NB)。实验中利用累计贡献率来比较2种算法的降维能力。本实验为了增加实验结果的精确性采用交叉验证的实验方法,每个实验做10组,求平均值。本文主要介绍在Wine数据集下实验的对比。
表1 UCI 3个数据集的描述信息

数据集类别特征数样本数Wine313178Breast Cancer Wisconsin232569Biodegradation2411055
3.2.2 实验分析
为了验证MIC-PCA算法的降维效果和分类性能,选取UCI机器学习库中的Wine数据集、Breast Cancer Wisconsin数据集和Biodegradation数据集分别进行PCA和MIC-PCA分析验证。在实验中采用随机抽样的方法对各个数据集进行实验,验证2种特征选择方法分类准确率采用的分类方法分别是k近邻算法(KNN)、支持向量机算法(SVM)和朴素贝叶斯算法(NB)。
实验1MIC-PCA算法的降维性能
实验中利用累计贡献率来比较2种算法的降维能力。本实验为了增加实验结果的精确性采用交叉验证的实验方法,每个实验做10组,求平均值。
比较两者得到的主成分的个数和累计贡献率,结果如表2所示。
表2 2种算法在Wine数据集下降维能力的比较

PCAMIC-PCA主成分个数主成分累计贡献率/%主成分个数主成分累计贡献率/%580.16583.71685.10690.45789.33793.33892.02896.30994.23999.281096.171099.33
从表2可以看出,同一个数据集降到相同维数情况下,MIC-PCA的主成分累计贡献率要高于PCA的主成分累计贡献率。
实验2MIC-PCA算法的分类性能
对Wine数据集、Breast Cancer Wisconsin数据集和Biodegradation数据集分别进行PCA和MIC-PCA计算后,用降维后得到的主成分作为新的特征,分别用k近邻算法(KNN)、支持向量机算法(SVM)和朴素贝叶斯算法(NB)进行分类,计算分类的准确率,比较两者分类性能。
图3为用Wine数据集测试采用PCA和MIC-PCA降维后分类的准确率。

(a) KNN分类

(b) SVM分类
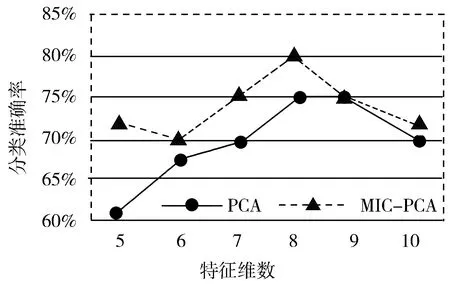
(c) NB分类图3 Wine数据集上2种算法降维后分类的准确率
从图3中Wine数据集分别利用PCA和MIC-PCA降维后做分类验证的结果可知,在Wine数据集上MIC-PCA降维后分类准确率比PCA降维后分类的准确率要高。
实验结果表明,根据实验1,在达到相同的降维效果时采用MIC-PCA方法后,所需的主成分个数更少,即MIC-PCA的降维效果比PCA降维效果更好;根据实验2,在相同数据集下根据降维结果选取同样的数据主成分个数进行分类准确率验证时,无论是采用KNN分类算法、SVM分类算法还是NB算法,采用MIC-PCA方法进行降维后,各算法对数据集的分类效果均变得更好。
4 数据挖掘过程可视化模式构建
在VISDMiner系统中,用户可以根据实际需要选择对应的数据挖掘算法,本系统目前实现的数据挖掘算法包括分类算法、聚类算法和多维关联规则算法。本文主要以K-means聚类数据挖掘算法为例,介绍K-means聚类算法的数据挖掘过程可视化的构建流程。
4.1 K-means算法过程可视化模式构建流程
K-means算法过程可视化模式构建步骤具体如下:
1)数据预处理。系统的数据预处理模块采用改进的主成分分析算法MIC-PCA对原始的高维数据集进行降维处理。
2)对挖掘数据目标的统计描述信息进行可视化展示,包括缺失值信息以及类别属性信息等,以帮助用户确定簇类数目。其中缺失值处理的方法有:临近点替换、序列均值替换、三次样条插值;统计信息描述采用的可视化技术有:散点图、折线图、条形图、3D散点图。
3)选择属性并对属性进行可视化展示。其中,采用基于属性关联性的ReliefF算法对筛选出来的特征子集作进一步的评价,用Ranker算法对ReliefF得到的属性权值进行排序,通过阈值设置显示用户要分析的属性[17]。
4)根据前面的数据统计描述信息的可视化展示,用户可以设置K-means算法参数,包括聚类数目k和算法迭代次数n,用以调整算法的执行。
5)K-means算法执行过程中的可视化内容包括:展示各簇数目所占比例(饼图和条形图)、展示最近簇类中心(报表)、展示多维数据(散点矩阵)、展示各簇间数据关联信息(平行坐标图)。
6)用户根据可视化挖掘结果的满意程度可以重新设置参数再次进行挖掘以此获得最优的挖掘结果。
4.2 K-means算法过程可视化应用实例

图4 Wine数据集数据统计信息可视化展示(条形图)
1)在采用K-means算法进行数据挖掘分析之前,VISDMiner系统可提供对数据统计描述信息的可视化,用以帮助用户了解数据的属性和类别信息。图4是VISDMiner系统采用条形图的可视化展示形式对UCI中Wine数据集数据统计信息进行描述。
图5是VISDMiner系统采用3D散点图可视化展示形式对UCI中Wine数据集数据统计信息进行描述。

图5 Wine数据集数据统计信息可视化展示(3D散点图)
2)VISDMiner系统允许用户在选择K-means进行数据挖掘分析时根据前述步骤的数据可视化展示信息以及自己的领域知识与经验去设置簇类的个数和聚类计算的迭代次数。通过这种交互手段并借助可视化技术,可以改变数据挖掘过程中所依据的条件,同时可以帮助用户直观地察觉到算法参数对挖掘结果的影响。
图6是用户设置簇类数目和聚类计算迭代次数后用饼状图展示K-means聚类计算的过程可视化结果。这种可视化方式很直观地展示了划分簇类的个数、各簇的划分比例以及簇类中包含数据的多少。

图6 K-means聚类计算的过程可视化结果(饼状图)
图7是采用散点矩阵图展示K-means聚类计算的过程可视化结果。散点矩阵是一个可以展示多维数据的可视化方法,它可以展示出每2个维度之间的关系[18-19]。每个小矩形是一个散点图,展示了2个属性之间的关系。散点的不同灰度表示不同的数据类别。

图7 K-means聚类计算的过程可视化结果(散点矩阵)
图8是采用平行坐标图展示K-means聚类计算的过程可视化结果。平行坐标图将高维数据的各个变量用一系列相互平行的坐标轴表示,以灰度做区分[17]。VISDMiner系统采用平行坐标图的可视化方法进行数据挖掘过程的展示可以反映样本变化趋势和各个变量间相互关系。

图8 K-means聚类计算的过程可视化结果(平行坐标图)
5 结束语
本文设计并实现了一个交互式数据挖掘过程可视化系统VISDMiner,用以协助人们从海量数据中提取各种有用的信息并根据可视化的中间结果集做出相应的决策。针对高维数据集的挖掘处理及可视化展示,本系统还提出了一种改进的主成分分析算法(MIC-PCA)对数据进行降维处理。实验结果表明,借助VISDMiner系统及其引入的用户交互,用户可根据自身领域知识和经验来更好地控制挖掘计算处理,更容易观察和理解挖掘过程中结果数据中隐含的信息,为下一步挖掘探索做出更优的决策。该系统采用的改进的主成分分析算法MIC-PCA相比传统的PCA算法具有更好的降维效果和更高的分类准确率。
参考文献:
[1] Martínez-Martínez J M, Escandell-Montero P, Soria-Olivas E, et al. A new visualization tool for data mining techniques[J]. Progress in Artificial Intelligence, 2016,5(2):137-154.
[2] Bouali F, Guettala A, Venturini G. VizAssist: An interactive user assistant for visual data mining[J]. Visual Computer, 2016,32(11):1447-1463.
[3] Krzywicki A, Wobcke W, Bain M, et al. Data mining for building knowledge bases: Techniques, architectures and applications[J]. Knowledge Engineering Review, 2016,31(2):97-123.
[4] Chen Hongmei, Li Tianrui, Luo Chuan, et al. A decision-theoretic rough set approach for dynamic data mining[J]. IEEE Transactions on Fuzzy Systems, 2015,23(6):1958-1970.
[5] 马昱欣,曹震东,陈为. 可视化驱动的交互式数据挖掘方法综述[J]. 计算机辅助设计与图形学学报, 2016,28(1):1-8.
[6] Ben Steichen, Giuseppe Carenini, Cristina Conati. User-adaptive information visualization: Using eye gaze data to infer visualization tasks and user cognitive abilities[C]// Proceedings of the 2013 International Conference on Intelligent User Interfaces. 2013:317-328.
[7] 周芳芳,李俊材,黄伟,等. 基于维度扩展的Radviz可视化聚类分析方法[J]. 软件学报, 2016,27(5):1127-1139.
[8] 张红军. 多维数据集中高维数据可视化算法研究[J]. 微电子学与计算机, 2017,34(5):110-113.
[9] Goodwin S, Dykes J, Jones S, et al. Creative user-centered visualization design for energy analysts and modelers[J]. IEEE Transactions on Visualization & Computer Graphics, 2013,19(12):2516-2525.
[10] 汤颖,钟南江,孙康高,等. 基于兴趣的社交网络用户聚类及可视化[J]. 计算机科学, 2017(s2):385-390.
[11] Niedoba T. Multi-parameter data visualization by means of principal component analysis (PCA) in qualitative evaluation of various coal types[J]. Physicochemical Problems of Mineral Processing, 2014,50(2):575-589.
[12] Xie Shengkun, Jin Feng, Krishnan S, et al. Signal feature extraction by multi-scale PCA and its application to respiratory sound classification[J]. Medical & Biological Engineering & Computing, 2012,50(7):759-768.
[13] Reshef Y A, Reshef D N, Finucane H K, et al. Measuring dependence powerfully and equitably[J]. Journal of Machine Learning Research, 2016,17(1):7406-7468.
[14] 范雪莉,冯海泓,原猛. 基于互信息的主成分分析特征选择算法[J]. 控制与决策, 2013,28(6):915-919.
[15] Reshef D N, Reshef Y A, Finucane H K, et al. Detecting novel associations in large data sets[J]. Science, 2011,334(6062):1518-1524.
[16] Shim J E, Lee I. Weighted mutual information analysis substantially improves domain-based functional network models[J]. Bioinformatics, 2016,32(18):2824-2830.
[17] 李玮瑶,赵凯. 基于特征提取的网络热点事件挖掘算法[J]. 计算机与现代化, 2015(5):17-20.
[18] Jürgen Bernard, Martin Steiger, Sven Widmer, et al. Visual-interactive exploration of interesting multivariate relations in mixed research data sets[C]// Proceedings of the 16th Eurographics Conference on Visualization. 2014:291-300.
[19] 孟海东,蔺志举,徐贯东. 可视化数据挖掘工具的设计与实现[J]. 计算机与现代化, 2011(6):132-135.

