一种创意折叠桌参数设计的数学模型及仿真
(北京航空航天大学计算机学院 ,北京 100083)
0 引 言
折叠与伸展已成为家具设计行业普遍应用的一个基本设计理念,具有折叠结构的家具因其运输、存储方便,节约空间,富有个性而渗透到家居行列中[1,2].韩佳成在2012年介绍了由荷兰设计师 Robert van Embriqs 设计的一款折叠桌[3],使用时可折叠支立在地面(如图1所示[4]),不用时可展开为一个矩形平板(如图2所示[4])。

图1 折叠桌实物图

图2 折叠桌折叠演示图
这种折叠桌的主体结构是若干条被截断的可折叠等长木条,每根木条被截断成三段,截断处通过合页连接,以实现折叠.所有木条通过两跟钢筋串连到一起,钢筋两端分别固定在桌腿各组最外侧的两根木条上.其余木条必须开有一定长度的空槽以保证折叠时钢筋滑动的自由度(见图3).

图3 桌腿开槽形状
这种折叠桌虽然结构简单,但是由于其形成过程是从一个平面结构向一个三维造型的折叠过程,所以其有关参数的设计尤为重要. 文献[6]和[7]给出了桌面为圆形的折叠桌动态折叠的数学模型,并利用Matlab进行了模拟.
研究的重点是建立折叠桌面边缘为任意凸函数的折叠桌动态折叠过程的一般数学模型,并利用Maple[8]软件进行折叠过程仿真模拟.通过仿真模拟,分析各个参数对折叠桌的影响.在此基础上,建立相关加工参数的计算公式.
1 折叠桌折叠过程的数学模型
1.1 主要参数的符号及说明
所涉及的折叠桌参数包括桌子高度(不包括木板厚度,用H表示)、桌子宽度(用D表示)、桌面形状(可用一个凸曲线方程y=f(x)表示其一侧边缘曲线)、最大折叠角度(即最外侧桌腿与水平方向的夹角,用θ表示).材料参数包括木条长度(用L表示)、木条宽度(用w表示)及木条厚度(用v表示).用n表示木条个数.加工参数的名称、符号、意义见表1:

表1 折叠桌加工参数表
上述的提及的形状参数、材料参数及加工参数都称为设计参数,这些参数的意义也可在图4中体现出来.

图4 主要设计参数示意图
这类折叠桌的设计主要是针对以上的设计参数进行选定和优化计算,使得产品轻便美观、折叠灵活、支立稳当、加工方便、用材最少.特别是折叠角度θ、钢筋位置参数c及槽孔长度参数ci对折叠桌的整体效果起着至关重要的作用,而且这些参数之间互相关联,所以必须建立相应的数学模型,进行优化设计和仿真.
1.2 折叠桌的数学模型
首先建立坐标系:以地面为xOy面,以木条构成的平板平放地面时的中心为坐标原点,以与木条平行的方向为y轴,向上方向为z轴方向建立直角坐标系(如图5所示).

图5 坐标系
木板在提升折叠过程中,着地的木条端点不一定总是第1个和第n个木条的4个端点.为建模方便,在折叠过程中我们总设第1个和第n个木条对应的4个桌脚(即木条端点)位于地面(即xOy面),这样,其它木条的端点就有可能伸到xOy面以下,从而这些点的竖坐标就有可能为负值,当折叠角度达到一定程度时,就只有最外侧(即第1个和第n个木条)的4个桌脚着地,其他木条端点悬空,从而才能使桌子放稳.
不失一般性,假设桌面的形状是由凸曲线y=f(x)(f(x)≥0),y=-f(x)及木板最外侧两根木条所在直线围成的对称图形.由前述符号可知桌面宽度为nw,记
(1)
即a等于桌面宽度的二分之一.令li表示第i根木条对应的桌腿长度,则
(2)
这里,木条的序号是从x轴负半轴距离原点最远处的木条开始算起.从而所需木条的长度L为
L=2r1+2l1.
(3)

b=r1+l1
(4)
显然应有r1 为便于动态仿真模拟,引入一个动态控制变量h来表示折叠过程中桌面离开地面的高度,显然0≤h≤H. 下面针对任意h∈[0,H],建立每个木条对应的桌面线段和桌腿线段的方程. 对于第i个木条,其折叠后形成的折线记为AiBiCiDi,其中Ai、Di为该木条的底面中线端点,Bi、Ci为两个截断面底线中点,位于桌面底面边缘.钢筋穿过桌腿AiBi和CiDi的两个点分别记为Ni和Mi. 由于AiBiCiDi所在的平面平行于yOz坐标面,故Ai、Bi、Ci、Di4个点的横坐标均为 xi=-a+(i-0.5)w (5) 从而Bi,Ci两点的坐标分别为 Bixi,-f(xi),h,Cixi,f(xi),h (6) 因此BiCi的参数方程为 (7) 其中,xi由式(5)确定. 由于钢筋垂直yOz面,故对所有i(1≤i≤n),Mi都具有相同的纵坐标和竖坐标,设这两个数分别为y0和z0,由对称性,所有Ni的纵坐标和竖坐标分别为-y0和z0. 由前述假设,A1、D1、An、Dn总是在地面上,故它们的竖坐标总是为0. 这时,点Ni与N1的投影点重合,记为N,点Mi与M1的投影点重合,记为M,则N和M的坐标分别为N(0,-y0,z0)和M(0,y0,z0). 因此,M点的纵坐标y0和竖坐标z0的表达式为 注意到点M与Mi具有相同的纵坐标和竖坐标,所以Mi的坐标为 从而结合式式(6),可得DiCi所在直线的方向向量为 (8) 又注意到Di点到Ci点的距离即为第i个木条对应的一条桌腿长,从而有 故得 代入(8)式,便得Di的坐标为 (9) 其中 根据对称性,Ai的坐标为 (10) 从而可得桌腿AiBi和CiDi的方程分别为 (11) (12) 至此,式(7),(11)和(12)就是当折叠高度为h时,每个木条折叠后的所形成的空间造型的数学模型. 图6 第i个木条与第1个木条在yOz面上的投影 模型中,参数r1,l1,a及b都是间接参数,通过式(1),(2),(3)和(4)获得,而这些表达式中,需要给定形状参数H,θ,材料参数w,n,其中H是想要折叠桌的高度,可根据不同的需要确定,一般在40 cm到70 cm之间选取.θ反应折叠程度,若θ太小,则桌脚容易在地面打滑,使桌面平摊到地面,而且由式(1)和(3)可知,需要的木条长度L也变大,造成材料浪费;但θ太大(比如接近90度),则桌子脚距太小,使得桌子头重脚轻,容易翻倒.一般选取θ时,最好使桌面边缘在地面的投影刚好落在四个桌脚上.另外,若地面很光滑,则尽可能取接近90度的值,若地面较粗糙,则可适当减小,一般选取70-80度为宜.木条宽度w可根据需要的桌面宽度选取,但不宜太宽,因为太宽会使开槽难度增加,而且影响美观,一般以2 cm到5 cm为宜.木条个数n由桌子宽度决定.y=f(x)反映了桌面的形状,要求为光滑的凸曲线,比如半圆,椭圆等.钢筋位置参数c是影响桌子折叠效果和其它加工参数最主要的因素,在以下的仿真模拟中将进一步讨论. 采用Maple 软件编程,得到针对以上参数的折叠桌动态折叠过程三维效果图(如图7所示). 再次,在图7中,对位置参数k分别取0.3、 0.4、0.5、0.6、0.7和0.8,而让其它参数保持不变,通过编程得到如图9所示的仿真模拟效果图. 由图9可以看出,当k太小(k<0.3)时,折叠的部分桌腿会碰到一起,在实际中无法实现充分折叠,同时美观性也较差;而当k太大(k>0.7)时,钢筋会露在有些桌脚下面,这意味着这些桌腿开槽时桌脚一端也要开槽,在实际中这些桌腿将移出钢筋,从而整个木条将无法固定,这是不允许的.同时,k越大,开槽长度也越大,增加了加工难度.因此,k的选取应该使钢筋位置在外侧桌腿的中部为宜,即最好取k=0.5. 图7 折叠桌折叠过程三维效果图 a 椭圆型 b 操场型 在折叠桌的所有参数中,有些是根据实际需要事先选定的,诸如桌子高度H、宽度D、木条宽度w、厚度v等,有些要根据实际情况和经验取定值,比如折叠角度θ和钢筋位置参数k(如前所述).当这些参数的值取定后,其它参数就要通过模型进行计算. 其次,需确定每根木条的截断位置.对于第i个木条,其截断点Bi和Ci距离木条中心的距离实际就是ri,即该木条位于桌面部分长度的2倍,从而计算式为 (13) 再次,需确定钢筋位置参数c.如前所述,c=kl1,l1由式(2)计算,一般取k=0.5. 最后,需确定每根木条的开槽长度.对于第i个木条,钢筋的初始位置(即整个木板平铺时钢筋穿过该木条的位置)距离该木条中心的距离为c,折叠后钢筋位于Mi和Ni点,对应于投影点M和N(如图4所示),所以可得在第i个木条上的开槽长度为 注意到 故有 (14) 特别的,当i=1时,由于r1=f(x1),故由上式易得c1=0;当i=n时,由于r1=rn=f(xn),也可得cn=0. 图9 不同钢筋位置参数的折叠桌模拟图 木条序号12345678910ri7.80613.17016.53618.99820.87922.32623.41924.20624.71724.969ci0.0004.3587.66510.37012.59514.39715.80816.84917.53617.878 图10是根据上述数据绘制的加工参数示意图,其中,Bi和Ci是截断点,开槽的地方用阴影表示,不同木条开槽长度不同. 图10 截断位置和开槽长度示意图 建立了一种折叠桌折叠过程的一般性数学模型,通过编程仿真模拟验证模型的正确性,同时也说明仿真模拟程序的正确性和可行性.同时通过仿真模拟的直观性来讨论各个设计参数的可行性,可为进一步产品设计提供较好的理论参考. 在研究中,重点考虑了模型建立的仿真模拟,对关键参数之间的关联关系和最优设计未做深入讨论,特别是折叠角度对稳定性的影响以及钢筋位置参数的最优设计还需做进一步理论分析. 参考文献: [1] 雷忠兴.折叠结构在家具设计中的应用[J].现代装饰(理论),2014(5):10-12. [2] 林佳欣,聂桂平.基于TRIZ理论的折叠家具设计研究[J].东华大学学报(自然科学版),2011,37(4): 518-521. [3] 韩佳成.平板折叠边桌[J].设计,2012(8):25-25. [4] Smoyu. Robert van Embriqs 创意组合折叠餐桌.中国设计之窗, http://www.333cn.com/ industrial/sjxs/133003.html. [5] 2014年高教社杯全国大学生数学建模竞赛赛. http://www.mcm.edu.cn/problem/2014/cumcm 2014problems.rar. [6] 蔡志杰. 创意折叠桌的设计[J]. 数学建模及其应用, 2015, 4(1): 66-74. [7] 王秋森,党展鹏,庄文华,等. 平板折叠桌的设计模型[J]. 数学建模及其应用, 2015,4(1): 23-32. [8] 何青,王丽芬. Maple教程[M].北京:科学出版社,2006.



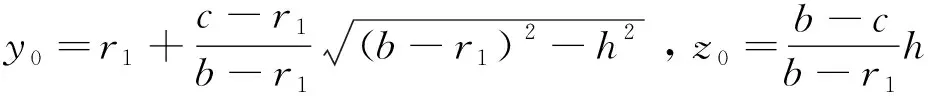

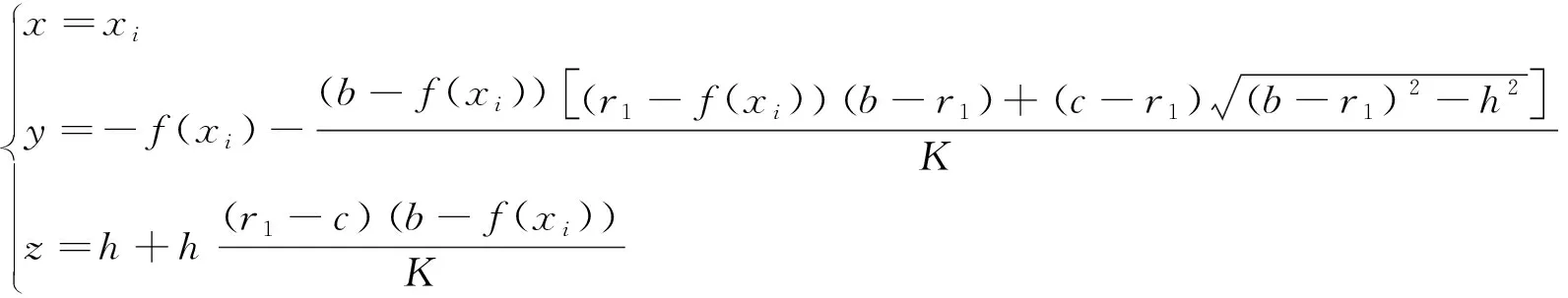

2 折叠桌的动态仿真模拟及关键参数分析
2.1 设计参数的初步分析
2.2 折叠过程仿真模拟及关键参数分析



3 折叠桌的加工参数计算
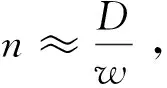
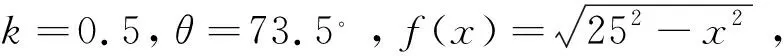



4 结 论

