基于实测载荷谱和仿真载荷谱的底盘疲劳分析及对比
荣 兵, 肖 攀, 周建文
(中国汽车工程研究院股份有限公司, 重庆 401122)
载荷谱作为车辆结构疲劳性能分析的基础,按照其获取的方式的不同大致可分为两类:① 实测载荷谱;②仿真载荷谱。由于六分力仪及载荷谱采集技术的发展,实测载荷已作为各车企研究疲劳性能的重要基础数据而被熟知,且通过对试验场进行载荷谱采集,也容易得到实测载荷谱[1]。基于试验场实测载荷谱的车辆结构件载荷分解、疲劳分析及优化也得到了广泛的应用[2-5]。然而载荷谱采集却受到较多的限制,需具备开发车型的骡车,采集试验耗时较长,成本较高,导致疲劳分析及优化阶段延后,在结构件开发前期无法有效地支持结构疲劳性能的优化。近年来,由于疲劳仿真轮胎模型和路面高程扫描技术的发展[6-7],使得基于试验场虚拟路面获得的疲劳仿真载荷谱的工程应用价值越来越显著,获取仿真载荷谱的前提是必须具备与试验场一致的三维虚拟路面模型,以及精确的疲劳仿真轮胎模型,从而在研发前期运用多体动力学仿真技术,仿真获得耐久性能分析的载荷谱,用于预测其疲劳寿命。
以某车型底盘疲劳性能对比分析为例,本文从以下几方面开展研究:①利用惯性基准的道路几何谱采集系统测得某试验场共振路2的中线轨迹数据和5路纵向高程数据,进行3D虚拟路面的重构;②建立该车型整车多体动力学模型,基于3D虚拟路面动态仿真,获取仿真载荷谱;③以实测载荷谱为基准,将仿真轴头载荷谱与实测轴头载荷谱在时域、频域和损伤3个方面进行对比;④基于实测载荷和仿真载荷谱对底盘疲劳进行仿真分析及对比,最终验证了基于虚拟路面仿真载荷谱的精确性,及较高的工程应用价值。
1 共振路2虚拟路面建立
1.1 路面高程的采集及处理
路面高程采集设备为中国汽研自主研发的惯性基准的道路几何谱采集系统。该系统的核心部件为激光检测梁,安装于采集车辆前部,如图1所示。该梁中集成了加速度传感器与激光位移传感器,可测试出5个激光头下在路面纵断面上的局部几何轮廓特征曲线,激光传感器具体布置详,如图2所示。该系统的具体测试原理在文献[8-9]中已有详细的说明。该系统的采样频率为22 kHz,有效地保证了在20~100 km/h的采集速度下,最小采用间距为1 mm,同时系统中集成了GPS系统,同步对行驶轨迹进行记录,采样频率为20 Hz。

图1 惯性基准的道路几何谱采集系统Fig.1 Road geometry spectrum acquisition system based on inertial reference

图2 激光传感器布置图Fig.2 Laser sensor arrangement
对国内某试验场路面高程进行扫描,其中部分路面高程数据如图3所示。其中包括6个通道数据,1通道~5通道为测试的5个激光传感器位置的路面纵向高程曲线,6通道为路面的纵向距离,结合5个高程曲线即反馈出路面在纵断面方向上的5个剖面图,其次由GPS系统采集的路面轨迹,如图4所示。

图3 路面高程数据Fig.3 Pavement elevation data
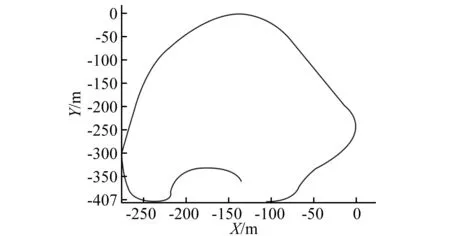
图4 路面轨迹Fig.4 Road track
由于文中仅对共振路2进行研究,图5为依据路面轮廓特征的共振路面高程分割示意图。其次,基于采集时间同步原则,得到的共振路轨迹曲线,如图6所示。
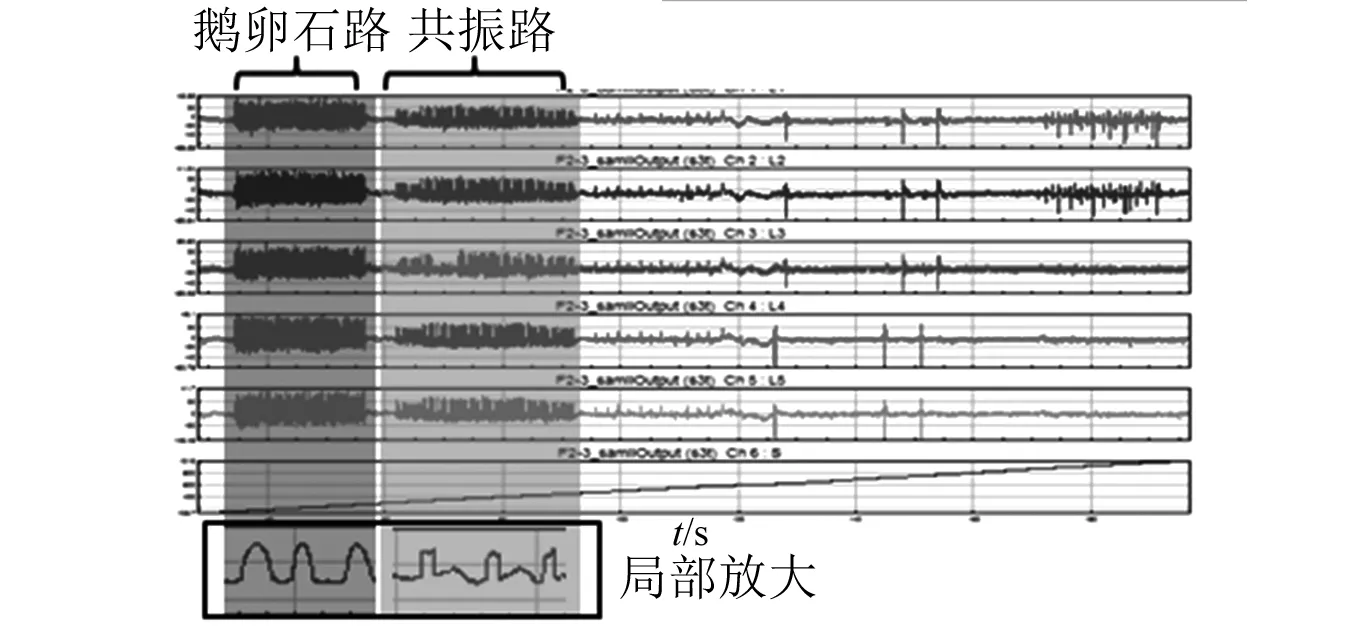
图5 共振路2高程分割Fig.5 Resonance 2 elevation segmentation

图6 共振路2轨迹曲线Fig.6 Track of resonance 2
分割后的数据按照虚拟路面纵向分辨率要求,进行路面高程数据的等距离抽样。对于共振路2,纵向采用5 mm等间距分辨率,对其局部轮廓特征已经能够全面反映。再将路面轨迹数据由经纬度转化为平面坐标的X值、Y值,由于其采集频率较低,在此不进行等距抽样,需拟合后,再与高程数据同步等距抽样。
1.2 3D虚拟路面的建立
由于采集高程数据在横向仅为5组数据,不足以构建3D虚拟路面,需要在路面横向按相应的分辨率进行插值。对共振路2的横向特征进行分析可知:该路面左右侧横向几何特征在纵向90°夹角方向一致(见图7),根据该特点,共振路2横向几何特征可采用线性插值得到,其线性插值示意是如图8所示。以路面左侧插值为例进行说明,由于横向几何特征与路面中线成90°夹角,则可依据左侧激光头1和激光头2同步采集的数据H(1,n)和H(2,n)线性插值出横断面上任意位置的高程数据H(c,n),其中H(1,n)中数字1表示第1个激光传感器采集的数据,n表示第n个采集点,同理H(2,n)为第2个激光传感器采集的第n个高程,H(c,n)中的c表示第c条插值曲线[10]。

图7 共振路2特征示意图Fig. 7 Characteristic sketch map of resonance 2

图8 共振路2横向插值图解Fig. 8 Horizontal interpolation diagram for resonance 2
其次,虚拟路面要实际反映路面的轨迹信息,故再根据采集的GPS信息进行路面中心轨迹复原。由于路面的GPS轨迹数据精度较低,利用matlab的3次样条插值复原路面轨迹中线[11],其中图9为GPS数据与拟合数据的对比图,实线为GPS数据,虚线为拟合的路面轨迹。在动力学仿真中,虚拟路面的起始点,及路面方向需与整车动力学模型原点,及行进方向一致,故对于拟合后的路面中线轨迹,需按照动力学仿真软件中的方向进行坐标转换,其原理如图10所示。以路面中线起始点作为新坐标系原点,前进方向作为新坐标系的X方向,则图中X′OY′坐标系统为新的坐标系。新坐标系确认后,计算出新旧坐标系中横轴之间的夹角α,依据式(1)和式(2)计算出新坐标系下路面中线坐标值。

图9 GPS数据与拟合数据对比图Fig.9 Comparison of GPS data and fitting data

图10 路面中线坐标转化原理Fig.10 Principle of the road line coordinate transformation
(1)
(2)
式中:X′n,Y′n为新坐标系下第n点的坐标值;Xn,Yn为旧坐标系下第n点的坐标值。实线为转换后的路面轨迹,虚线为转换前路面轨迹,如图11所示。

图11 路面轨迹转换前后对比图Fig.11 Comparison of road track conversion before and after
最后结合虚拟路面格式的要求,利用matlab编制实现对共振路2的三维虚拟路面重构,如图12所示。

图12 共振路2虚拟路面Fig.12 3D virtual road of resonance 2
2 实测载荷谱与仿真载荷谱的对比
2.1 实测载荷谱的获取
实测载荷谱采用六分力传感器进行采集,传感器参数,如表1所示。共振路2下,该车辆前左轮的六分力采集数据,如图13所示。

表1 六分力传感器参数说明

图13 六分力采集数据Fig.13 The load data from wheel force transducer
2.2 整车多体动力学模型建立
在耐久仿真的整车动力学模型搭建过程中,为确保整车多体动力学模型与实车在外部激励下动态响应的一致性,在保证悬架系统准静态K&C特性一致的前提下,还需注意一下几个方面:①衬套参数的调整,包括刚度曲线延伸,衬套阻尼设置;②柔性体部件的选择,以及柔性体部件的阻尼设置;③各部件质心、质量和惯量参数设置。
考虑整车动力学模型中弹性元件参数时,在结合实测参数数据的同时,需根据其结构特征对其极限范围进行拟合,以及实车装配状态下的限制,对各参数进行调整,从而达到仿真模型与实车的一致性,且保证模型在高载荷区域的适用性。考虑到实车装配限制的参数调整,如图14所示。由于在试验台进行衬套Z向刚度测试时,沿Z向的平动没有受到限制故Z向位移到达±40 mm(见调整前曲线)。当装配到实车上时,Z向平动受到副车架板件的限制Z向位移仅在±8 mm内(见图15),故考虑到其安装位置的限制,对于衬套的阻尼可来源于实测值,或者通过线性刚度值的0.5%来估算。

图14 摆臂前衬套Z向线刚度Fig.14 Z direction stiffness for arm front bushing

图15 摆臂前衬套实车装配图Fig.15 The assembly drawing of arm front bushing
针对车型的悬架形式,选择变形部件进行柔性体建模,该车型中柔性体建模部件为前稳定杆和后扭力梁。其次,影响动态仿真载荷的参数还包括车辆各部件的惯量、重量和质心等物理参数。开发中的车型,利用3D设计模型或有限元模型均可得到比较准确的数据。最终依据该车型的参数信息、装配关系,搭建的整车多体动力学模型,如图16所示。包括前后悬架、动力总成、转向、轮胎和车身系统,模型中轮胎采用动力学软件集成的Ftire_205/55R16轮胎模型。
2.3 仿真载荷谱获取
在建立了虚拟试验场和整车动力学模型的基础上,如果要提取虚拟路面的耐久动态载荷,还需具备相应的事件文件,用于驱动整车动力学模型按照试验场规范在虚拟路面上进行动力学仿真。事件文件的实质同驱动控制文件dcf一样是仿真管制核心文件,由于事件文件是XML格式,为了便于阅读、修改和新建,MSC公司在ADAMS/Car中集成了一个名为事件建造器(Event Building)的工具[12]。
根据载荷谱采集过程中车辆速度、档位信息,以及建立的3D虚拟路面的中线轨迹数据编制事件文件,从而驱动整车模型在3D虚拟路面上的动力学仿真,车辆的仿真行驶状态与实车采集行驶状态完全一致,如图17所示。仿真完成后,即可提取车辆轴头的六分力和各部件接口点的动态载荷。

图16 整车多体动力学模型Fig.16 Vehicle multi-body dynamics model

图17 整车动力学仿真Fig. 17 Vehicle dynamics simulation
2.4 实测与仿真载荷谱的轴头力对比分析
将基于3D虚拟路面仿真获取的左前车辆轴头力数据与实测数据进行时域对比分析,图18~图20分别为纵向力FX、侧向力FY和垂向力FZ的时域曲线对比(虚线为仿真数据,实线为实测数据)。由此可见,3个方向力的趋势及大小基本一致,其中X向仿真数据在正值区域略大于实测数据,然而在负值区域却略小于实测数据,Y向仿真数据略大于实测数据,Z向仿真数据略小于实测数据,分析原因在于轮胎模型并没有按照实际轮胎性能进行参数辨识,所以在刚度上存在一定的偏差。仿真中采用轮胎型号为205/55R16,实际轮胎型号为195/60R16,仿真轮胎模型胎宽比实际轮胎较大,也是造成仿真侧向力FY较大的原因之一。

图18 左前轮FX时域对比Fig. 18 Time domain comparison for left front wheel X direction force

图19 左前轮FY时域对比Fig.19 Time domain comparison for left front wheel Y direction force

图20 左前轮FZ时域对比Fig.20 Time domain comparison for left front wheel Z direction force
进一步从频域对轴头力进行对比,图21~图23分别为纵向力FX、侧向力FY和垂向力FZ的频域曲线对比(虚线为仿真数据,实线为实测数据)。从图中分析可知,在车辆姿态频域段(约5 Hz)和弯曲扭转频域段(约20~30 Hz),仿真的数据的幅值均大于实测数据,主要是由于多体模型中车身采用刚体单元模拟与实车的振动特性存在一定的差异造成;在路面垂向激励频域阶段(约10~15 Hz),X和Y方向的仿真与实测数据的幅值基本一致,而Z方向上实测数据的幅值大于仿真数据,主要是Z向载荷受路面垂向激励影响较大,且实车采集过程中质心随着配载物体的移动导致载荷会发生一定的转移,故而导致仿真与实测数据的偏差。总体上看,频域曲线也验证了FY的时域仿真数据略大于实测数据,FX和FZ的时域仿真和实测数据基本一致的情况。其次虽然3个力信号的频域曲线存在一定差异,但激励频域段都介于0~60 Hz,车辆结构件疲劳分析主要采用准静态疲劳分析方法,故频域曲线的一定偏差对疲劳分析结构影响可以忽略,而疲劳性能的主要影响因素还是考虑时域下的变化趋势和幅值大小,通常用伪损伤对比可以得到量化,实测与仿真轴头力的伪损伤对比详见表2,其中相差最大为Y向,比值为2.95,相差最小为Z向,比值为0.70。该比值范围也进一步验证了仿真与实测数据的一致性,以及仿真数据的有效性和实用性。其后对底盘的疲劳分析及对比也验证了以上观点的正确性。

图21 左前轮FX频域对比Fig.21 Frequency domain comparison for left front wheel X direction force

图22 左前轮FY频域对比Fig.22 Frequency domain comparison for left front wheel Y direction force

图23 左前轮FZ频域对比Fig.23 Frequency domain comparison for left front wheel Z direction force

前左轮轴头力伪损伤实测仿真比值FX1.59 1.47 0.93 FY0.05 0.14 2.95 FZ9.99 6.94 0.70
3 底盘部件的疲劳仿真分析及对比
考虑到底盘的不同部件主要承受作用力的不同,为全面地对比两种载荷谱下疲劳性能的差异,故选择摆臂和转向节进行疲劳分析对比,摆臂主要承受X和Y向力作用,转向节同时承受3个方向的力作用。
按照疲劳分析建模要求建立摆臂和转向节的有限元分析模型(见图24和图25)。摆臂焊缝采用节点耦合的方式模拟,且为了避免局部应力集中,焊缝单元全部采用四边形单元模拟,并根据各焊缝的类型在疲劳分析时进行相应的设置。转向节采用四面体单元模拟,为提高模拟精度,单元进行二次节点处理。

图24 摆臂有限元模型Fig.24 Finite element model of arm

图25 转向节有限元模型Fig. 25 Finite element model of knuckle
采用惯性释放的方法,分别计算部件连接点各方向单位载荷的应力。结合各方向的单位载荷应力和基于仿真载荷谱与实测载荷谱获得的疲劳分析动态载荷,计算有限元模型中各节点的时域应力数据,其次采用雨流计数法对应力循环进行统计[13],应用Goodman曲线进行应力修正,结合材料的S-N曲线,计算单次循环损伤,在利用Miner法则进行疲劳损伤累计[14-15],最终两种载荷谱下的摆臂疲劳分析结果,如图26和图27所示,转向节疲劳分析结果,如图28和图29所示。由于转向节在单次共振路2作用下损伤很小,故进行了1010倍的放大。
为了更好的对疲劳结果分布区域和疲劳损伤大小进行对比,在部件中各取3个区域进行对比,摆臂3处的节点号分别为15 445,13 591和6 676,其中节点15 445处为疲劳损伤最大处,各具体位置,见图26和图27。对比结果,如表3所示。所选择的3个对比点,仿真与实测载荷的疲劳分析结果比值范围为1.71~1.79,差异仅0.08,说明两者的疲劳分析结果分布趋势的一致性很好,该结论从图26和图27的损伤云图也能得到很好的验证。其次节点13 591处损伤比值最大为1.79,两者的损伤结果偏差还不及2倍,说明两者的疲劳分析结果的一致性也很好。其次由于摆臂疲劳损伤主要受FX和FY的影响,在表2轴头力对比中FX与FY伪损伤比值分别为0.93和2.95,均值为1.94,与疲劳分析损伤比值也基本一致。

图26 实测载荷谱摆臂疲劳分析结果Fig.26 Fatigue analysis results of measured load for arm

图27 仿真载荷谱摆臂疲劳分析结果Fig. 27 Fatigue analysis results of simulated load for arm

对比节点损伤实测仿真比值15 4452.263 7E-0054.019 4E-0051.78 13 5911.400 0E-0092.500 0E-0091.79 6 6762.250 4E-053.853 8E-051.71

图28 实测载荷谱转向节疲劳分析结果Fig. 28 Fatigue analysis results of measured load for knuckle

图29 仿真载荷谱转向节疲劳分析结果Fig. 29 Fatigue analysis results of simulated load for knuckle
转向节中疲劳对比的3个区域节点号分别为12 287,99 653和14 550,其中节点12 287处为疲劳损伤最大处,各具体位置可详见图28和图29。对比结果,如表4所示。所选择的3个对比点,仿真与实测载荷的疲劳分析结果比值介于0.43~2.43,总体而言,两者的疲劳分析结果及分布趋势的一致性较好。其中最大比值点位于转向节与摆臂的连接区域主要承受X和Y向力,故该区域疲劳损伤比值与表2中FX和FY轴头力伪损伤比值的均值基本一致。其余两个节点处由于受Y向力影响较小,仿真载荷下的损伤较实测载荷的要小,与表2中FX和FZ轴头力伪损伤比值趋势一致。

表4 转向节疲劳分析结果对比
综上所述,虚拟路面仿真载荷谱和实测载荷对底盘部件的疲劳分析结论一致性很好,验证了3D虚拟路面建模和整车多体动力学模型建模的准确性,以及较高的工程应用价值。
4 结 论
由于疲劳仿真轮胎模型和路面高程扫描技术的发展,使得基于试验场虚拟路面获得的疲劳仿真载荷谱的工程应用价值越来越显著。文中先建立某试验场的共振路2的3D虚拟路面和某车型的整车多体动力学模型,利用3D虚拟路面和多体动力学模型仿真得到仿真载荷谱,并通过试验获取该车型在共振路2上的实测载荷谱,在时域、频域和伪损伤方面对两种载荷谱进行对比,验证了两者的一致性,进而对该车型底盘的疲劳性能进行分析对比,验证了两种载荷谱对疲劳分析结果在分布及大小上均存在很好的一致性。
通过对比分析,也进一步验证了3D虚拟路面的建模方法,整车动力学模型建模方法的精确性,以及基于试验场3D虚拟路面提取的疲劳载荷谱的精确性。但从影响仿真载荷谱的因素来分析,以下两方面还有待于在今后的研究中得以提升:
(1)整车多体动力学模型中,车身柔性体的应用。采用一般的柔性化方法,车身柔性体占用计算资源较大,且会导致仿真无法进行,故后期应在考虑车身柔性体的同时,进行相应的简化。
(2)整车多体动力学模型中,轮胎模型的应用。对轮胎进行测试,辨识出载荷谱采集时轮胎的Ftire模型。
参 考 文 献
[ 1 ] 荣兵,肖攀,周建文,等. 基于实测载荷谱的载荷分解及后桥疲劳分析 [J].汽车工程学报,2016, 6(3): 203-211.
RONG Bing, XIAO Pan, ZHOU Jianwen, et al.Dynamical load cascading and rear axle fatigue analysis based on road load spectrum[J].Chinese Journal of Automotive Engineering, 2016, 6(3): 203-211.
[ 2 ] 方剑光,高云凯,徐成民. 车身疲劳载荷谱的位移反求法[J]. 同济大学学报(自然科学版),2013, 41 (6): 895-899.
FANG Jianguang, GAO Yunkai, XU Chengmin. Displacement back-calculation of body fatigue loading spectrum[J]. Journal of Tongji University(Natural Science), 2013, 41 (6): 895-899.
[ 3 ] 毛显红,肖攀,陈建华,等.基于道路谱的汽车车身疲劳分析[J].计算机辅助工程,2011, 20(2) : 75-78.
MAO Xianhong, XIAO Pan, CHEN Jianhua, et al. Automotive body fatigue analysis based on road spectrum[J]. Computer Aided Engineering, 2011, 20(2) : 75-78.
[ 4 ] 卲建,董益亮,肖攀,等. 基于多体模型仿真的载荷谱虚拟迭代技术分析 [J]. 重庆理工大学学报(自然科学),2010, 24(12): 84-87.
SHAO Jian, DONG Yiliang, XIAO Pan, et al. Journal of Chongqing University of Technology (Natural Science), 2010, 24(12): 84-87.
[ 5 ] 冯金芝,刘乐,郑松林. 某轿车悬架系统的载荷仿真分析[J]. 汽车工程,2012, 34(10) : 913-917.
FENG Jinzhi, LIU Le, ZHENG Songlin. Load simulation analysis on a car suspension system[J]. Automotive Eng, 2012, 34(10) : 913-917.
[ 6 ] YANG X, MEDEPALLI S. Comfort and durability tire model validation[J]. Tire Science and Technology, 2009, 37(4): 302-322.
[ 7 ] BAECKER M, GALLREIN A, HAGA H, A tire model for very large tire deformation and its application in very severe events[J]. SAE International Journal of Materials and Manufacturing, 2010, 3(1): 142-151.
[ 8 ] 段虎明,石锋,赵永杰,等. 道路路面的剖面曲线测量研究及实践[J]. 振动与冲击,2011,30(3):155-160.
DUAN Huming, SHI Feng, ZHAO Yongjie, et al. Research and practice of road surface profile measurement[J]. Journal of Vibration and Shock, 2011, 30(3): 155-160.
[ 9 ] 严金霞,张开斌,谢飞,等. 基于ADAMS的非平直路面模型的重构与验证[J]. 汽车工程,2011, 33(11): 985-989.
YAN Jinxia, ZHANG Kaibin, XIE Fei, et al. Reconstruction and validation of non-straight road model based on ADAMS[J]. Automotive Engineering, 2011, 33(11): 985-989.
[10] 荣兵,肖攀,周建文,等. 某试验场强化路三维虚拟路面重构与对比分析[J]. 汽车工程,2017,39(2): 214-219.
RONG Bing, XIAO Pan, ZHOU Jianwen, et al. Reconstruction and comparative analysis on 3D virtual intensified road in a proving ground[J]. Automotive Engineering, 2017,39(2): 214-219.
[11] 董霖. MATLAB使用详解[M]. 北京: 科学出版社,2008.
[12] 陈军. MSC.ADAMS技术与工程分析实例[M]. 北京: 中国水利水电出版社,2008.
[13] POWER E.Cycle counting methods and the development of block load fatigue programmes:780102 [R]. [S.l]:SAE, 1978.
[14] 周传月,郑红霞,罗慧强. MSC.Fatigue疲劳分析应用与实例[M]. 北京:科学出版社,2005.
[15] 王国军. nSoft疲劳分析理论与应用实例指导教程[M]. 北京:机械工业出版社,2007.

