考虑不完全维修的风电机组齿轮箱维修策略优化

上海绿色环保能源有限公司 ■ 黄琛 张智伟

上海电力学院电气工程学院 ■ 寻健*

0 引言

系统或部件的维修方式主要有事后维修和预防性维修两种。事后维修是在系统或部件发生故障后采取维修措施；预防性维修是指当系统或部件正常运行一段时间后，在预定的时间内对其进行维修，以防止部件发生故障，造成更大的损失。海上风电机组由于位置偏远，人员接近和维护都比较困难。因此，相比于事后维修，预防性维修可以降低风电场的运维成本，提高收益，增加风电机组的可用率。

国内外研究者对风电机组的运维策略进行了大量的研究。文献[1]考虑到经济相关性，提出了一种基于可靠度的风电机组关键部件确定性机会维修策略，以实施风电机组的优化维修，可有效节省风电机组全寿命期的总维修成本。文献[2]针对风电机组关键部件维修会产生昂贵的固定维修费用、停机损失及发电损失的问题，提出了一种预防性机会维修策略，以机会维修可靠度裕度为优化变量对总维修费用进行优化，最终获得最小维修费用和最优维修决策。

事后维修和预防性维修都可以有效节约维修成本，但是这些策略都是基于设备运行时的故障统计数据或现场人员的经验，而未考虑设备运行时的检测状态的变化情况[3-4]。

近年来，相比基于时间的维修模式，基于状态的维修模式被认为是一种更有效的维修模式，它是基于设备当前或预测的退化状态采取的维修措施。这种维修模式受到学者的关注并提出一些状态评估模型和状态维修模型[4-7]。文献[4]提出了一种基于风电机组各部件状态退化过程的机会维修策略，制定状态维修阈值函数和机会维修阈值函数，并通过维修成本最小的方法确定它们。文献[8]在文献[4]的基础上考虑风电机组可修系统的维修建模，提出了一种基于风电机组状态的不完全机会维修策略，定义维修因子ε对应不同的维修程度，以反映不完全维修的效果，这种建模更符合实际情况，最后的仿真分析验证了该策略的有效性和可行性。

文献[1-8]考虑了各种因素，但是都未考虑设备中关键部件的循环利用和循环次数的问题。而在实际情况中，部件无法无限制地进行维修，经过一定次数的维修后，部件必将要进行报废处理。因此，本文针对这个问题考虑了风电机组关键部件的循环利用问题，借助维修因子ε来描述风电机组关键部件的不完全维修。根据维修因子ε取值的不同，利用单位时间内平均收益最大的方法来确定部件的预防性维修阈值和部件全寿命周期内最优的维修次数，最终达到单位时间运行最大的目的。最后通过Matlab仿真，验证所提出的风电机组齿轮箱维修策略优化的有效性和实用性。

1 基于可靠度的部件循环利用策略

对于一个由关键部件构成的系统或设备，利用“可靠度”来定义系统中关键部件的维修概念。而基于可靠度的确定性的预防性维修是指系统或关键部件的寿命是确定的，不考虑部件运行过程中发生的随机故障。也就是说，对部件的可靠性进行分析，若部件的可靠性降低至预防性维修的阈值时，结合该部件的可靠度函数可以获得它的预防性维修的时间间隔，这时需对该部件进行预防性维修。图1给出了一个部件预防性更换的原理示意图。

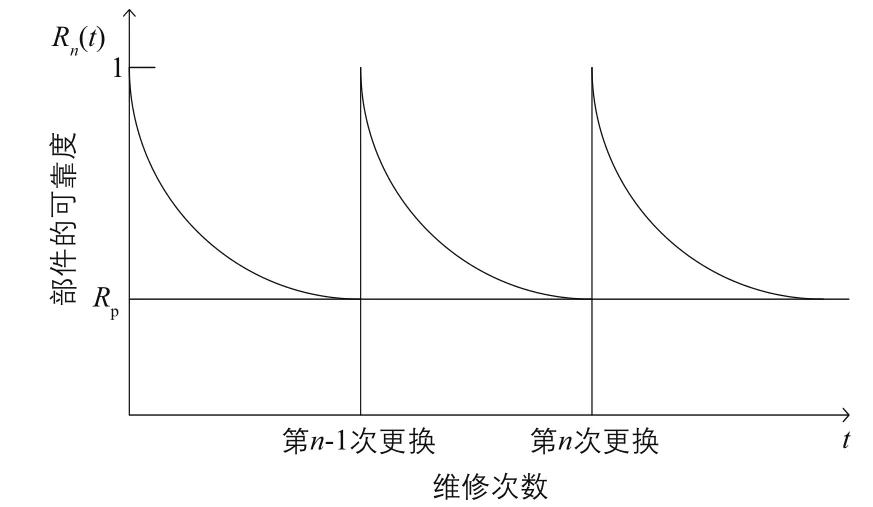
图1 基于可靠度的预防性更换维修策略

本文在预防性维修的基础上，提出了关键部件的循环利用策略。在实际情况中，设备不可能经过无限次的维修后还能继续发挥作用，而是经过一定次数的循环利用后进行报废。在设备的循环过程中，应考虑设备的不完全维修，因为设备在经历过上一次维修后，会对下一次的运行产生3种影响，分别是“恢复如新”“恢复如旧”“恢复到介于如新和如旧之间”。基于此，可以定义一个维修因子ε(0＜ε≤1)来描述上一次的维修对下一次运行的影响。当ε=1时表示完全维修，维修后的部件恢复如新，可靠度恢复到1；当0＜ε＜1时，表示不完全维修，维修后的部件恢复到介于如新和如旧之间的状态，可靠度得到一定程度恢复。

2 风电机组不完全维修模型

2.1 风电机组威布尔分布模型

风电机组由于运行情况复杂，运行环境恶劣，关键部件的故障率会随时间的变化而变化。根据风电机组的故障统计可知，风电机组关键部件的劣化过程一般服从两参数的威布尔(Weibull)分布。那么，部件的失效分布密度函数可由式(1)表示：

式中，t为部件运行时间；β为形状参数；η为尺度参数。

由式(1)可推导出分布函数为：

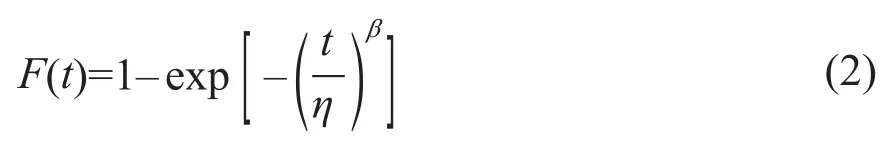
由式(2)可推导出可靠度函数为：

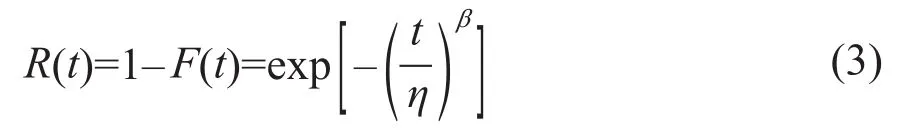
由式(1)、式(3)可推导出故障率函数为：

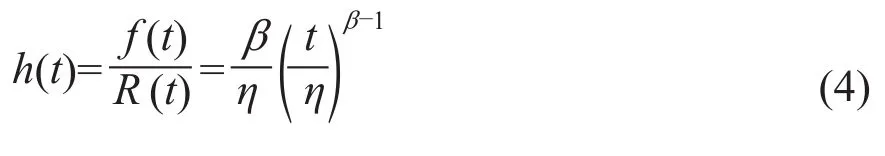
2.2 风电机组部件不完全维修模型

由于海上风电机组大都运行在环境恶劣的海洋环境中，风电机组部件的状态受环境影响较大。因此，若对风电机组的关键部件采取不完全维修策略，可以改善部件的运行状况，使经过维修的风电机组可以恢复到维修前某一时刻的状态，提高风电机组的可靠度，延长风电机组的寿命。采用不完全维修因子ε对风电机组关键部件维修方式建模，可以反映风电机组部件经过维修后无法恢复如新，只能下降到此次维修前的状态，因此可以计算出部件经过不完全维修后的可靠度函数。不完全维修后的可靠度变化情况如式(5)所示。

式中，n为一个周期内的不完全维修次数。

按照上文的预防性维修策略，在风电机组关键部件的可靠性降低到预先设定的预防性维修阈值Rp时执行不完全维修。因此，部件的可靠性方程也可表示为：

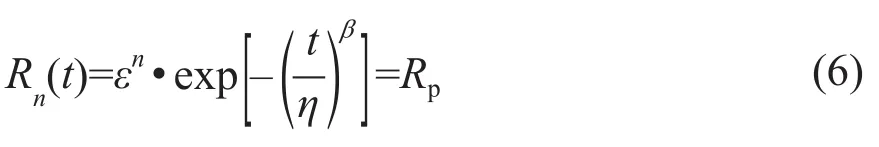
当部件进行不完全维修时，每个周期的运行时间都不相同，根据式(6)可以求出部件不完全维修时的各个运行周期Tn为：

联立式(5)～式(7)，可以推导出风电机组全寿命周期内的可靠度变化情况。

由图2可知，部件初始状态为全新状态，经过一段时间运行后，达到预防性维修阈值Rp时进行不完全维修。维修以后的初始可靠度将低于上一个周期的初始可靠度，如在tn-1时刻的初始可靠度小于之前运行周期的初始可靠度。

2.3 维修策略介绍

为了建立所提出的维修策略，需要先做出以下假设，以便于建立风电机组齿轮箱的不完全维修模型[9]：1)风电机组的状态由关键部件的状态表示，关键部件执行维修或更换意味着风电机组执行维修或更换，部件从全新状态开始运行，部件服从威布尔分布。2)部件有2种维修方式，若部件采用不完全维修方式，则可以改善性能但不能恢复如新；若部件采用更换方式则可以使部件的状态恢复到全新。同时，不完全维修的成本小于更换成本。3)在一个部件的全寿命周期内，在更换前都是执行不完全维修，最后一次执行更换，使部件恢复如新。

风电机组齿轮箱的循环利用策略是指在风电机组齿轮箱达到预防性维修阈值Rp的基础上进行不完全维修，以期达到齿轮箱循环利用的目的，从而延长齿轮箱的使用寿命。

通过预设的预防性维修阈值Rp来确定部件的维修间隔，即部件的运行间隔；而不完全维修可以改善部件的性能，延长部件使用寿命。但随着部件不完全维修次数的增加，可获得的收益也越来越低，直到将其更换。图3为部件全寿命周期内考虑不完全维修的预防性维修策略的基本原理图。

图2 部件不完全维修可靠度变化过程

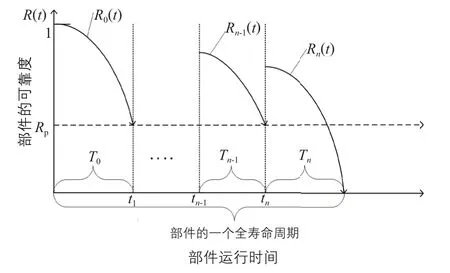
图3 考虑部件不完全维修的预防性维修策略

如图3所示，在T0周期，部件初始以全新的状态运行，当可靠度下降到预设的预防性维修阈值Rp时，即R1(t)≤Rp，此时在t1时刻对部件实施不完全维修，维修后的部件性能改善，可靠度得到一定程度的恢复；第n–1次不完全维修后，部件的可靠度函数变化为Rn-1(t)，在运行了Tn时间后，达到预防性维修阈值Rp，这时进行最后一次不完全维修后，部件的可靠度函数变化为Rn(t)；为了充分发挥部件的价值，最后一次部件运行了Tn时间直到发生故障再执行故障更换。

由图3可知，考虑了不完全维修的预防性维修策略，根据预设的预防性维修阈值Rp可以充分发挥部件的价值，同时减少故障带来的停机损失。采用不完全维修因子建模，可以更准确地对风电机组的齿轮箱进行维修，从而减少过度维修和缺少维修，延长部件使用寿命。

2.4 风电机组单位时间运行收益建模

可循环利用的风电机组关键部件，全寿命周期内考虑不完全维修的单位时间运行收益的模型可表示为：

式中，M(Rp,n)表示风电机组关键部件全寿命周期内的运行收益；Ccost(Rp,n)为一个周期内的运行维修费用；T为部件运行的一个周期。

式(9)是通过运行时间和单位时间的运行收益，求出风电机组运行的总收益。

式中，Cw为单位时间的运行收益；Tj为每次不完全维修后的运行时间，0≤j≤n；Rn(t)dt为最后一次作为不可修部件的平均故障间隔时间。

维修成本可表示为：

式中，Cf为每次不完全维修的费用；Ce为每次停机损失；Cr为采购一个新部件的费用。

运行周期T可表示为：

由式(11)中可知，部件全寿命周期的时间由两部分组成，分别为不完全维修时的运行间隔和最后一次作为不可修部件的平均故障时间

综上所述，将式(9)～式(11)分别代入式(8)，可将式(8)表示为：

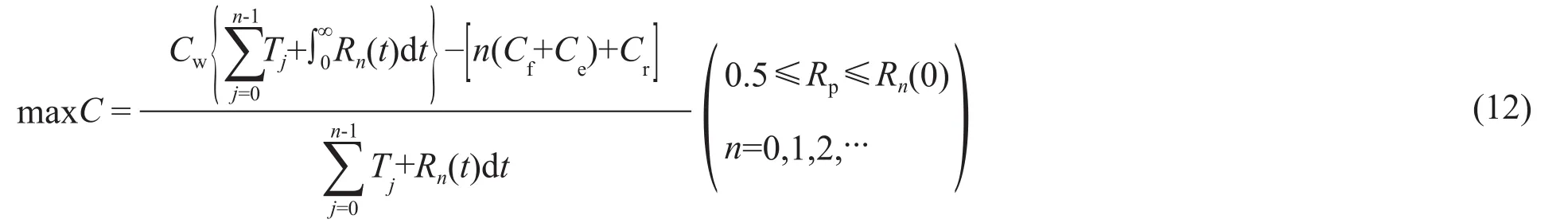
3 考虑不完全维修的策略优化算法

根据风电机组单位时间运行收益模型，可知2个决策变量Rp和n的选择直接影响维修的计划和最终的收益。由于是二维的优化变量，因此选用黄金分割法和枚举法相结合的方法，先在给定离散维修次数n的情况下，使用黄金分割法优化预防性维修阈值Rp，然后再计算不同维修次数、不同预防性维修阈值Rp时的单位时间运行收益值。

考虑不完全维修的风电机组关键部件齿轮箱维修决策过程如图4所示。

图4中，M是控制迭代次数；esp是精度控制；i表示迭代次数。对不完全维修次数n和预防性维修阈值Rp赋初值；然后在不完全维修次数n不变的情况下，用黄金分割法搜索预防性维修阈值Rp，使目标函数C最大；接着改变n的值使n=n+1继续循环，直到在约束条件下获得(Rp,n)使目标函数最大。

4 算例分析

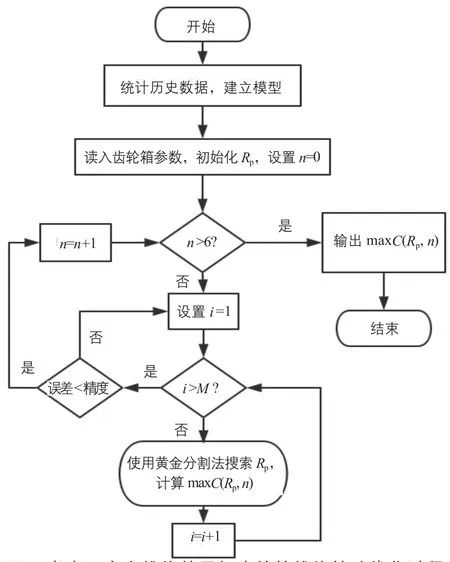
图4 考虑不完全维修的风机齿轮箱维修策略优化过程

现在选取风电机组中的齿轮箱作为关键部件进行分析，通过对风电场大型故障数据的统计分析可以获得齿轮箱的故障时间服从威布尔分布，表1给出了齿轮箱的威布尔参数和各种维修费用[10]。

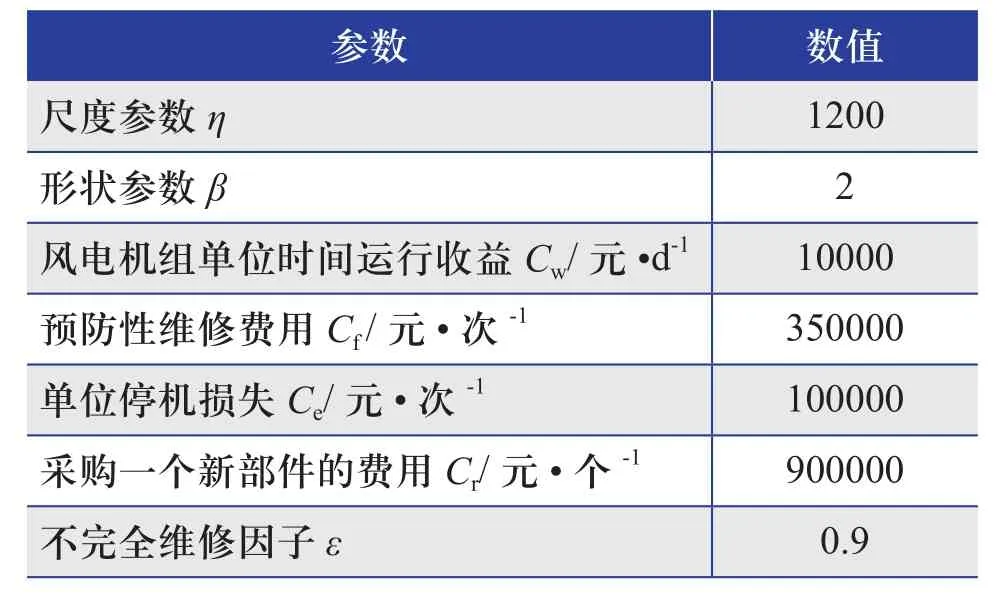
表1 齿轮箱各参数

将表1中的数据代入至式(12)中，优化风电机组中关键部件齿轮箱的预防性维修阈值Rp和一个全寿命周期内的不完全维修次数n，使单位时间的风电机组收益最大。将Rp=0.5、n=1和Rp=0.9、n=4代入公式(12)进行求解。

由图5可知，不同的预防性维修阈值和维修结果会影响风电机组单位时间的运行收益。若预防性维修阈值设置为Rp=0.7，可看出风电机组的齿轮箱维修1次的单位时间运行收益优于维修2次和3次的单位时间运行收益；若预防性维修阈值设置为Rp=0.6时，可看出齿轮箱维修2次时的单位时间运行收益优于维修3次、1次和4次时的单位时间运行收益；而当预防性维修阈值设置为Rp=0.5时，可看出在齿轮箱循环3次后，风电机组单位时间运行收益最大。

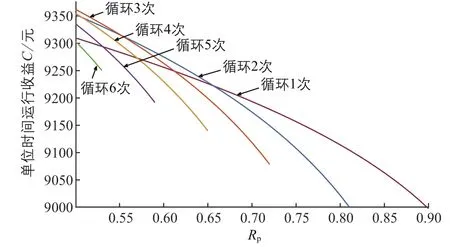
图5 不同循环次数、不同Rp时单位时间运行收益

由图6可知，关键部件的循环可以显著提升风电机组的单位运行时间收益，但并不是循环越多收益越大。当齿轮箱采用循环3次的预防性维修策略后，风电机组的单位时间运行收益最高为9362元/天，相比于只不完全维修1次时单位时间运行收益9310元/天提高了5.6%；虽然增加了2次预防性维修次数，增加了维修成本，但是延长了风电机组的使用寿命，减少了采购齿轮箱的成本，从而增加了风电机组的发电量，最终提高了风电机组的发电收益。而随着循环次数的增加，风电机组的单位时间运行收益开始加速下降，这样的结果符合实际情况。

图6 不完全维修次数参量寻优曲线

5 结论

本文提出的考虑不完全维修的预防性维修策略主要是围绕单台风电机组的单位时间运行收益进行分析，对风电机组在达到预防性维修阈值时进行不完全维修，虽然增加了维修成本，但可以延长风电机组的使用寿命，提高风电机组的发电收益。通过对风电机组维修策略仿真分析可以看出，相比于风电机组不进行维修发生故障后进行更换或只维修1～2次，对风电机组进行3次不完全维修后再进行故障更换可以显著提高风电机组的单位时间运行收益，同时也符合一般维修常识，说明了模型的合理性。

[1]赵洪山, 鄢盛腾, 张小田,等.风电机组确定性机会更换维修策略的研究[J].太阳能学报, 2014, 35(4): 568－575.

[2]赵洪山, 张路朋.基于可靠度的风电机组预防性机会维修策略[J].中国电机工程学报, 2014, 34(22): 3777－3783.

[3]Zheng X, Fard N.A maintenance policy for repairable systems based on opportunistic failure-rate tolerance[J].IEEE Transactions on Reliability, 1991, 40(2): 237－244.

[4]赵洪山, 张健平, 高夺,等.风电机组的状态——机会维修策略[J].中国电机工程学报, 2015, 35(15): 3851－3858.

[5]Ranger J, Ortner T M.Response Time Modeling Based on the Proportional Hazards Model[J].Multivariate Behavioral Research,2013, 48(4):503.

[6]Jardine A K S, Banjevic D, Makis V.Optimal replacement policy and the structure of software for condition‐based maintenance[J].Journal of Quality in Maintenance Engineering,1997, 3(2): 109－119.

[7]Wu X, Ryan S M.Optimal Replacement in the Proportional Hazards Model With Semi-Markovian Covariate Process and Continuous Monitoring[J].IEEE Transactions on Reliability, 2011,60(3):580－589.

[8]赵洪山, 张健平, 程亮亮,等.考虑不完全维修的风电机组状态——机会维修策略[J].中国电机工程学报, 2016, 36(3): 701－708.

[9]郑小霞, 李佳, 贾文慧.考虑不完全维修的风电机组预防性机会维修策略[J].可再生能源, 2017, 35(8):1208－1214.

[10]刘璐洁, 符杨, 马世伟,等.基于可靠性和维修优先级的海上风电机组预防性维护策略优化[J].中国电机工程学报, 2016,36(21): 5732－5740.