基于EMD的水轮机空化声发射信号阈值降噪方法

刘 忠， 宋嘉城， 邹淑云， 袁 翔， 周云贵， 陈 莹

(1. 长沙理工大学 能源与动力工程学院， 长沙 410114； 2. 清洁能源与智能电网湖南省2011协同创新中心， 长沙 410114； 3. 中国水利水电科学研究院， 北京 100038)

空化易造成水轮机能量特性下降、稳定性恶化，严重时会导致过流部件表面破坏、使用寿命缩短，威胁水电站的安全经济运行[1]。水轮机中发生空化时，伴随空泡瞬间形成和溃灭而产生的冲击波作用于叶片和管壁，将产生一种频率范围在20 kHz以上的声发射(AE)信号[2]。目前，国内外学者对水轮机空化声发射信号的研究取得了一定的成果。王辉斌等[3]研究了东江水电站2号水轮机空化声强烈度随负荷变化的趋势。Rus等[4]研究了某轴流式模型水轮机声发射信号的叶片流道调制等级相对数与空化数的变化规律。张俊华等[5]采用傅里叶变换对不同桨叶角度下的轴流转桨式水轮机的空化声发射信号进行频谱分析，研究了空化发展过程中声发射信号频谱特征的变化规律。He等[6]通过试验采用小波尺度谱研究了不同空化状态下空化噪声的时频特性及其与空化发展程度的关系。Schmidt等[7]基于声发射技术监测模型水泵水轮机的前缘空化，分析了声发射信号特征与图像观察结果之间的关系。由于受水轮机工作环境、采集仪器、测点位置和其他故障引发的冲击等因素影响，水轮机空化状态下采集到的声发射信号易被各种噪声污染，这些噪声的存在将直接影响后续的特征提取和状态识别。然而，对水轮机空化声发射信号降噪处理的研究尚不多见。

小波阈值降噪[8]是目前最常用的一种降噪方法，其机理是基于信号与噪声的小波系数在尺度上的不同性质，对不同尺度上的含噪系数采用相应阈值函数进行处理，以达到降噪目的。尽管该方法已经应用于很多领域，但在处理空化声发射信号这类非线性、非平稳性信号时存在小波基和分解层数选择上的局限性。经验模态分解(EMD)[9]是一种能够自适应地将非平稳信号分解为一组平稳的本征模态分量(IMF)的信号处理方法，不需要事先确定基函数和分解层数，整个分解过程完全是由信号自身决定的自适应过程，从而有效地克服了小波降噪的固有缺陷。目前，该方法已被应用于非平稳信号的降噪处理[10]，取得了较好的降噪效果。然而，受EMD自身局限影响，传统EMD降噪也存在降噪过度、局部噪声混叠和信噪比低等缺陷。

鉴于水轮机空化声发射信号的非平稳高频特性，笔者将小波阈值降噪思想与传统EMD降噪方法有效结合，建立了一种基于EMD的水轮机空化声发射信号阈值降噪(以下简称EMD阈值降噪)方法，并与小波阈值降噪方法、小波包阈值降噪方法和传统EMD降噪方法进行了比较。

1 传统EMD降噪

EMD的基本原理是根据给定信号x(t)的时间尺度，将原信号分解为一系列的平稳信号即IMF和一个趋势项的过程。每个IMF具有不同的时间尺度，包含了原信号不同尺度的局部特征信息，且从低阶到高阶恰好满足从高频到低频的系列分布，能够清晰地表现信号的特征信息。任意IMF要求满足：(1) 对于任意列数据，极值点个数与过零点个数相等或相差不大于1；(2) 由局部极大值点确定的上包络线与局部极小值点确定的下包络线的均值为0。EMD方法通过往复剔除信号中极大值、极小值组成的上、下包络线均值，使其严格满足IMF限定条件，将给定信号分解为有限个单分量信号。x(t)的EMD分解结果为：

(1)

式中：n为EMD分解后所得IMF总个数；Ij为EMD分解后第j阶IMF分量；rn为一个表示自适应趋势或常数的残余项。

任意信号经EMD分解后，各阶IMF分量所包含的频率成分随着阶数的增大由高到低逐次分布，且最高瞬时频率成分包含在第1阶IMF分量中[11]。因此，依据噪声的频率成分，找到噪声对应的IMF分量并加以剔除，便能达到一定的降噪效果。工程上噪声大多数分布在高频区[12]，主要包含在低阶的IMF分量中。传统EMD降噪方法就是判定前t-1阶主要为噪声成分，然后将其全部剔除。其降噪结果为：

(2)

2 阈值规则选取

阈值方法广泛应用于小波降噪处理过程中。阈值函数有2种主要形式：硬阈值和软阈值。两者的差别在于对变换系数进行阈值处理的规则不同。

硬阈值函数定义为：

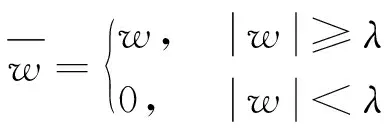
(3)

软阈值函数定义为：

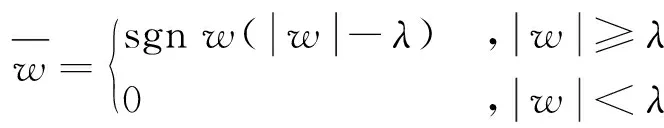
(4)

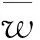
通常情况下软阈值法较硬阈值法能更好地保留信号的有用信息，所以多用于对工程信号的降噪。

阈值规则的选择对阈值降噪至关重要，直接影响降噪效果。常用的阈值规则分为自适应阈值和默认阈值2种。以下为自适应阈值处理的4种规则。

(1) 通用阈值规则(Sqtwolog)：采用固定的阈值形式。设含噪信号经小波分解后产生u个小波系数，噪声的均方差估计值为σ，则Sqtwolog阈值λ1为：

(5)

式中：σ=m/0.674 5，其中m为每一层小波系数的绝对中值。

(2) 无偏似然估计阈值规则(RigrSure)：是一种基于stein的无偏似然估计原理的自适应阈值规则。首先求取含噪信号经小波分解后的小波系数个数u，然后将每一层小波系数的平方由小到大排列，得到向量w=[w1，w2，…，wn]，且w1≤w2≤…≤wn，计算风险向量R=[r1，r2，…，rn]。

(6)

以R元素中的最小值rc作为风险值，由rc可求出对应的wc，则RigrSure阈值λ2为：

(7)

(3) 混合型阈值规则(HeurSure)：是一种结合Sqtwolog和RigrSure的最优预测变量阈值选择规则。设S为u个小波系数的平方和，令η=(S-u)/u，μ=(log2u)3/2/u1/2，则HeurSure阈值λ3为：

(8)

(4) 最小最大准则阈值规则(Minimaxi)：采用的是极大极小原理选择阈值。Minimaxi阈值λ4为：

(9)

文献[13]的仿真对比分析表明，HeurSure和Sqtwolog阈值规则的降噪效果要优于其他2种阈值规则，且HeurSure阈值是Sqtwolog阈值与RigrSure阈值两者的综合。

3 EMD阈值降噪方法

大量工程经验表明，噪声信号一般呈现高频特性，EMD分解后噪声模态分量主要集中在低阶IMF分量中，而水轮机空化声发射信号是一种高频信号。直接利用小波(包)阈值降噪难以摆脱基函数和分解层数选取对降噪效果的影响。若对其进行传统EMD降噪，将EMD分解后的含噪低阶IMF分量机械地剔除，然后再对剩余IMF分量进行重构，能达到一定的降噪效果，但会导致部分真实信号的缺失，造成降噪失真，对后期的信号特征提取研究产生不利影响。另外，采集信号由于受设备稳定性及环境干扰的影响易产生偏离基线。偏离基线的大小随时间变化而变化，会在采集信号频域内产生附加的低频成分，影响信号的时域和频域处理结果。由式(1)可以看出，若采集信号存在偏离基线，则产生的趋势项必然存在于EMD分解的残余项rn中。

因此，根据EMD自适应分解特性和阈值降噪的良好性能优点，提出了基于EMD的水轮机空化声发射信号阈值降噪方法，其流程图如图1所示。

图1 EMD阈值降噪流程图

该方法的具体实现步骤如下：

(1) 将采集的空化声发射信号X(t)进行EMD分解，得到一系列IMF分量Ii(i=1，2，…，n)和残余项rn。

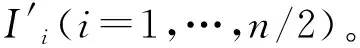
(10)

式中：Tj为该分量的阈值。

(11)

(12)

(13)

式中：L为信号长度；ηI=(SIj-L)/L，μI=(log2L)3/2/L1/2，SIj为第j阶IMF分量在信号长度L内的平方和；mIj为第j阶IMF分量的绝对中值；wIj由风险值求得。

(3) 剔除残余项rn，以消除趋势项影响。

(14)

4 仿真信号分析

由于描述水轮机空化声发射信号产生机理的数学模型尚未建立，故采用一个高频信号x(t)进行仿真。

x(t)=0.68sin(50 000πt)+0.25sin(360πt)+

0.758cos(300πt)+0.35sin(70 000πt)

(15)

采样点数取2 048。其波形图如图2所示。添加高斯白噪声，得到含噪仿真信号xn(t)(见图3)。

图2 无噪仿真信号x(t)

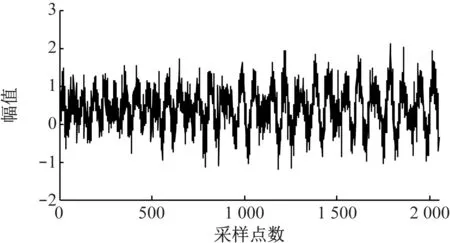
图3 含噪仿真信号xn(t)

对含噪仿真信号xn(t)分别用传统EMD降噪方法、小波阈值降噪方法、小波包阈值降噪方法和本文提出的EMD阈值降噪方法进行处理。选取db8小波为基函数，分解层数为四层，阈值规则为自适应阈值。降噪后的信号波形如图4所示。

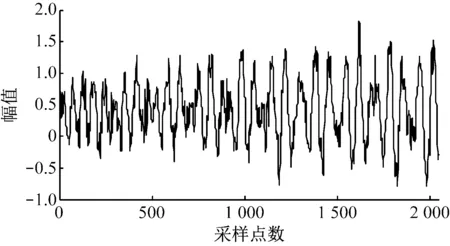
(a) 传统EMD降噪

(b) 小波阈值降噪

(c) 小波包阈值降噪

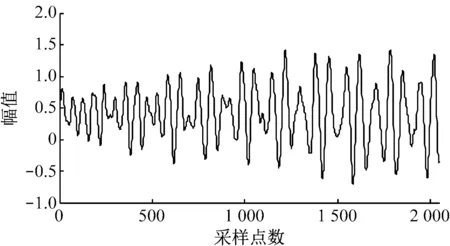
(d) EMD阈值降噪

由图4可以看出，4种方法处理后信号的波形轮廓与原信号基本一致。对比发现，图4(a)的降噪效果明显差于其他3种方法，图4(d)的波形较其他3种方法更平滑，且波形轮廓更接近原信号。采用常见的评价指标——信噪比(RSNR)和均方根误差(ERMSE) 进一步对比4种方法的降噪效果，结果见表1。

(16)

(17)

表1 4种方法降噪效果对比

由表1可知，降噪后的信号信噪比都比含噪仿真信号高，说明4种方法均具有一定的降噪作用。特别需要指出的是，经EMD阈值降噪方法降噪后信号的信噪比最高、均方根误差最小，总体降噪效果明显优于其他3种方法。

5 试验信号分析

在国内某座综合精度<±0.2%的闭式水轮机模型试验台上完成了混流式水轮机模型空化试验，同时采集了各工况下的声发射信号[14]。声发射传感器布置在混流式水轮机模型的导叶拐臂上。声发射信号采样频率设置为2.0 MHz，带通滤波频率范围为20～500 kHz。截取其中一段采样点数为2 048的声发射信号(见图5)进行分析，以检验EMD阈值降噪方法对实际空化声发射信号的降噪效果。

采集信号中不可避免地包含由工作环境背景噪声、采集仪器的电磁干扰、水力与机械相互作用引起的噪声等叠加而成的成分，这些会影响后续声发射信号特征提取的真实准确性。因此，采用上述4种方法对图5所示的信号进行降噪，降噪后的信号波形如图6所示。

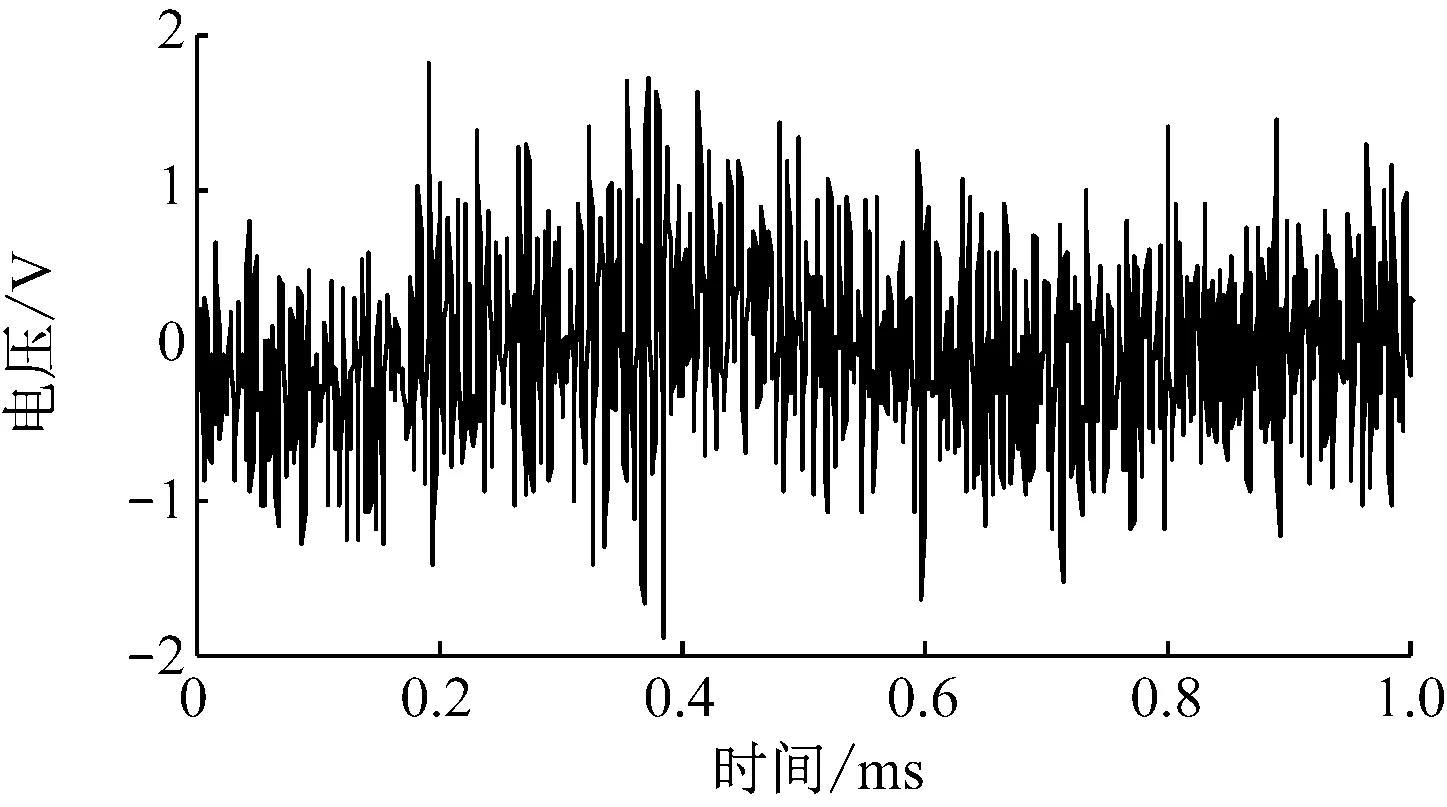
图5 混流式水轮机模型空化声发射信号

由图6可以看出，4种方法降噪后的波形保持了降噪前信号的波形轮廓与趋势，说明4种方法对混流式水轮机模型的空化声发射信号中的噪声成分都有一定的抑制作用。与含噪仿真信号不同，因为噪声源的复杂性，暂无法用信噪比或均方根误差对试验信号的降噪效果进行定量对比。因此，分别对图5和图6中的各信号进行快速傅里叶变换(FFT)，得到频谱图(见图7)，以便从频率成分分布上进一步对比各种方法的降噪效果。

(a) 传统EMD降噪

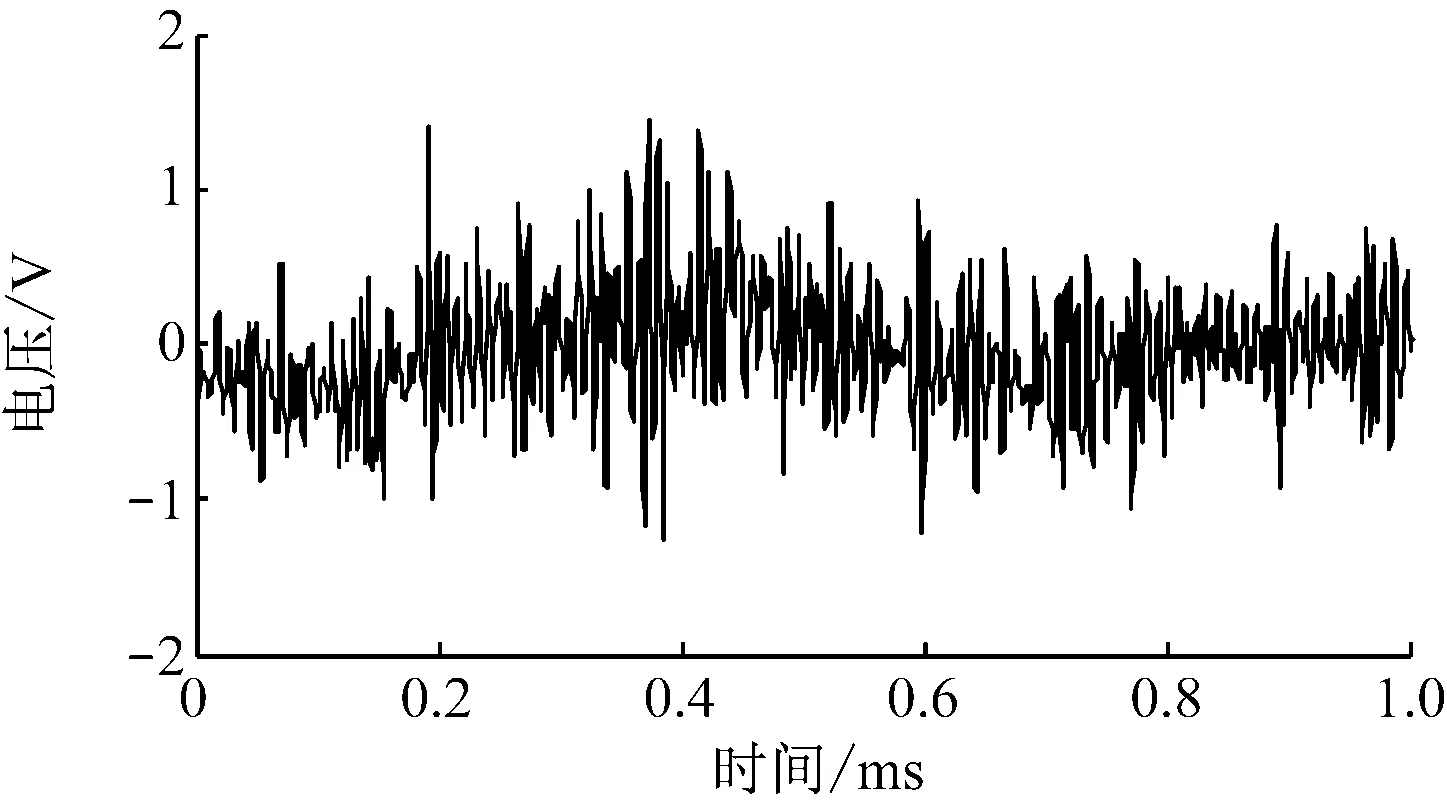
(b) 小波阈值降噪

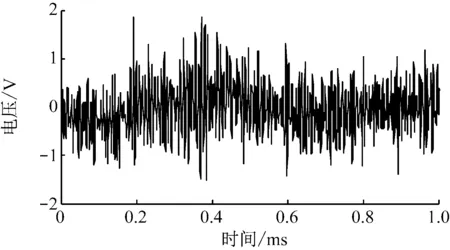
(c) 小波包阈值降噪

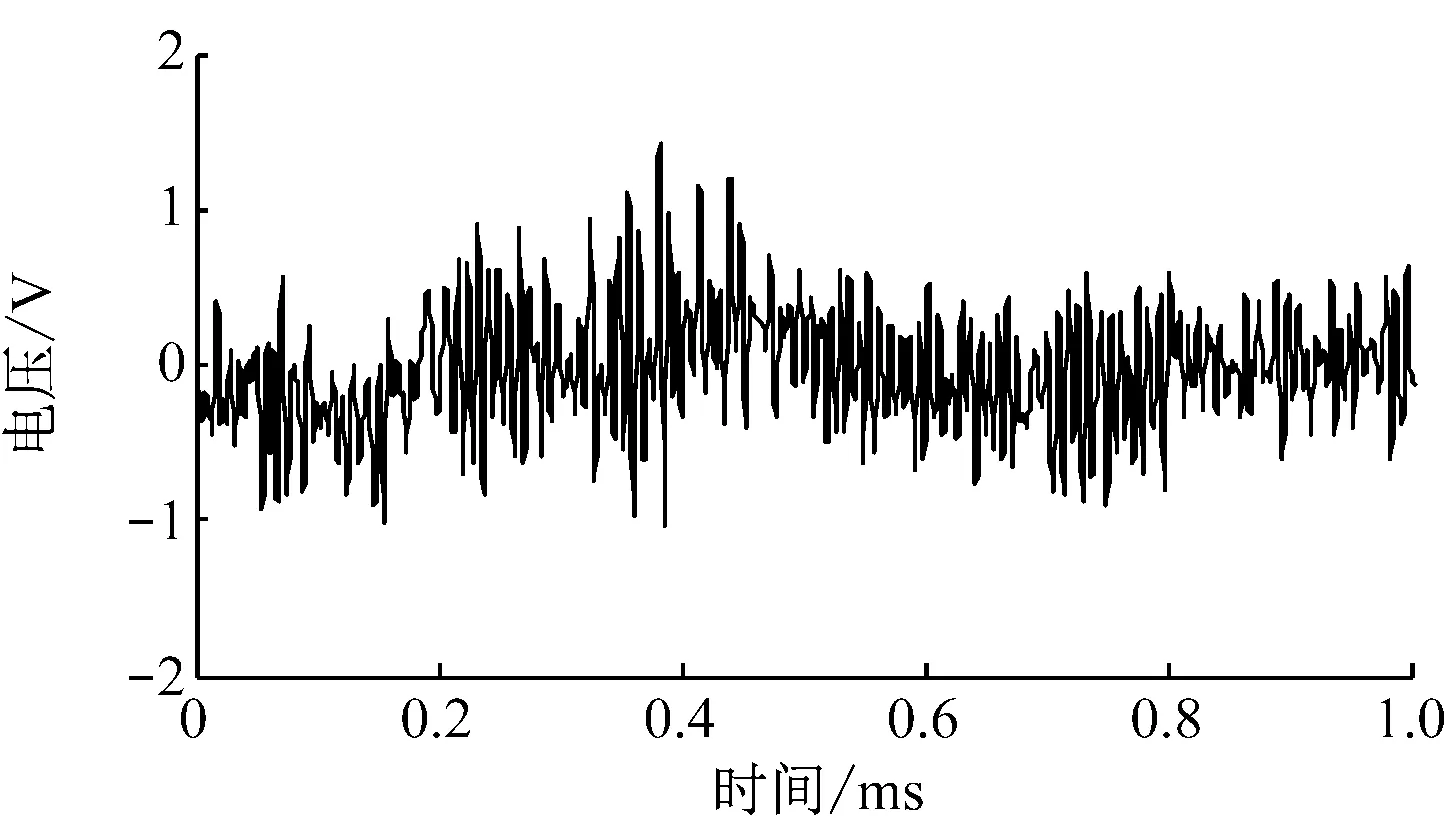
(d) EMD阈值降噪

通过图7可以发现，试验信号的频率成分分布在0～500 kHz，经4种方法降噪后信号的有效成分主要分布在30～180 kHz，这与文献[15]和文献[16]中空化声发射信号特征频段的描述基本一致。

图7(c)和图7(d)中保留有一定比例的200 kHz及以上频段的信号成分，这些残留成分无疑会对后续信号特征提取产生不利的影响。图7(b)中对200 kHz及以上频段的信号成分处理得较为彻底，然而30～180 kHz频段的幅值相对原信号和其他方法降噪后信号的幅值降低了很多，这一现象印证了传统EMD降噪方法存在的“降噪过度”的缺陷，部分真实信号成分缺失造成降噪后信号失真。而图7(e)在剔除200 kHz及以上频段噪声成分的同时，较好地保留了试验信号的有效成分，表明EMD阈值降噪方法优于其他3种方法。

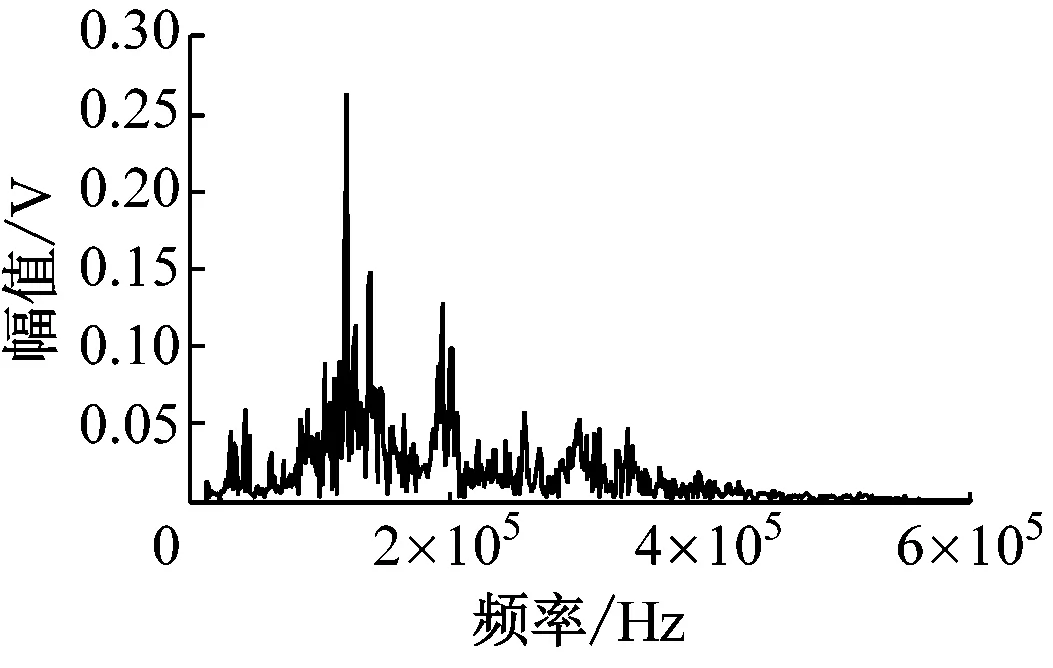
(a) 混流式水轮机模型空化声发射信号频谱

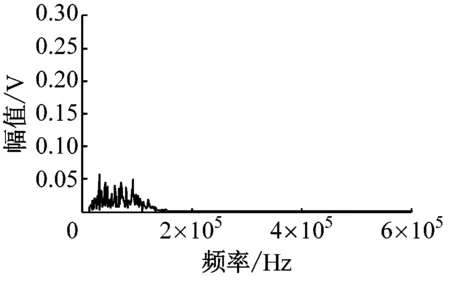
(b) 传统EMD降噪后信号频谱

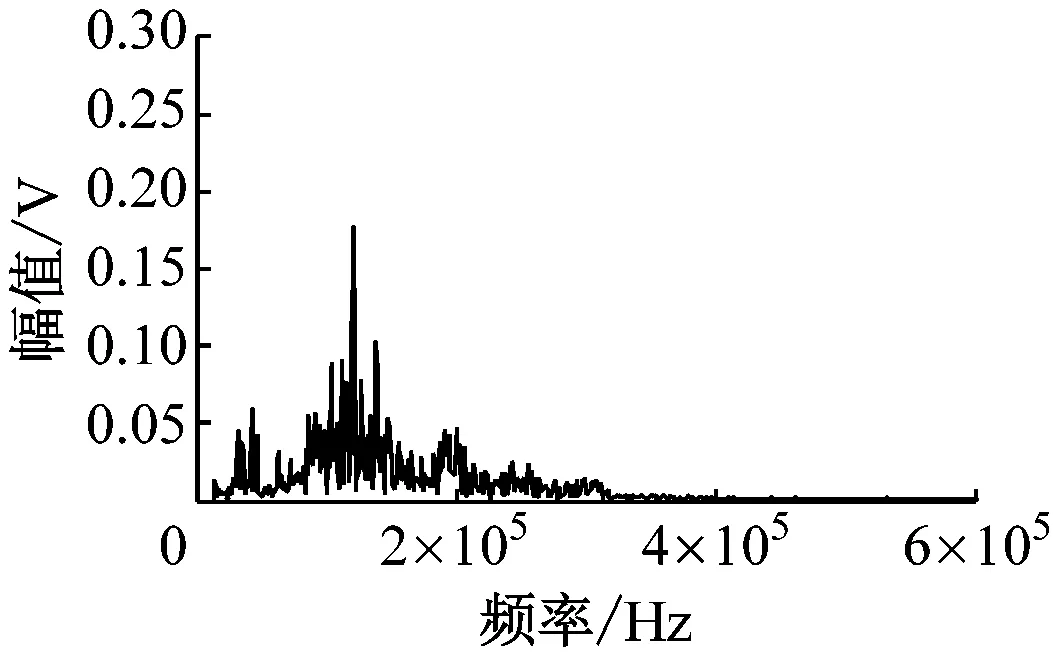
(c) 小波阈值降噪后信号频谱

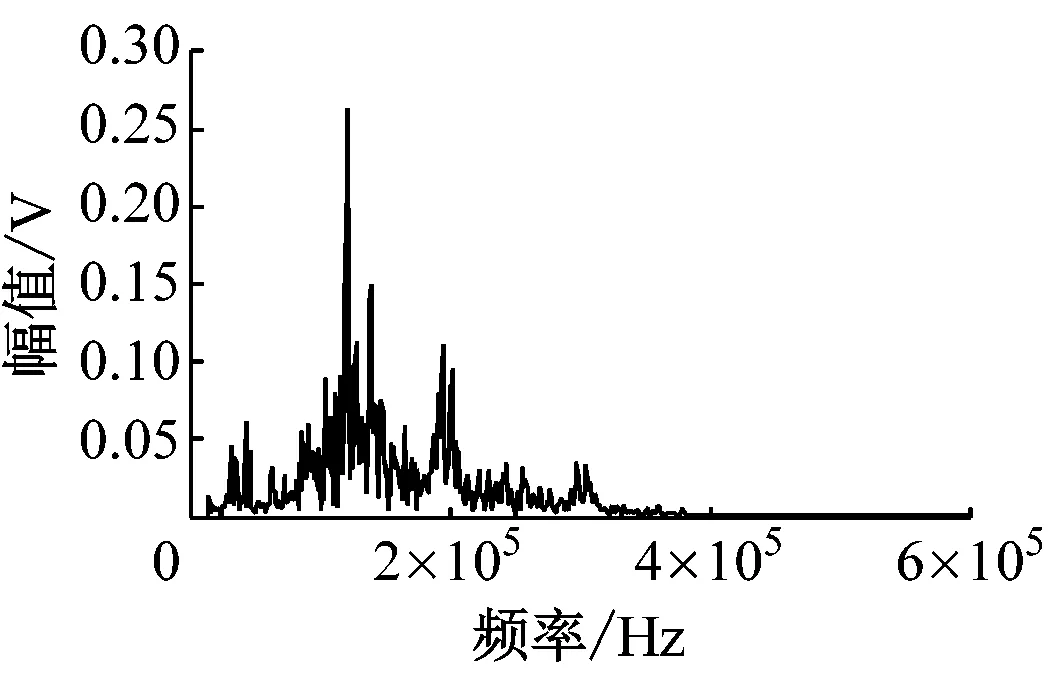
(d) 小波包阈值降噪后信号频谱

(e) EMD阈值降噪后信号频谱

6 结 论

(1) EMD阈值降噪方法有效结合了EMD和阈值降噪的优点，极大地克服了传统EMD降噪方法的机械性缺陷和小波(包)阈值降噪方法中存在的小波基函数与分解层数选取的局限性。整个分解过程是由信号自身特性决定的自适应降噪过程。

(2) 将EMD阈值降噪方法应用于水轮机空化声发射信号降噪处理这一领域。仿真及试验数据分析表明，该方法对水轮机空化声发射信号降噪处理较小波阈值降噪方法、小波包阈值降噪方法和传统EMD降噪方法更具优势。

参考文献：

[1] LUO X, JI B, TSUJIMOTO Y. A review of cavitation in hydraulic machinery[J].JournalofHydrodynamics, 2016, 28(3):335-358.

[2] HUSIN S, ADDALI A, MBA D. Feasibility study on the use of the acoustic emission technology for monitoring flow patterns in two phase flow[J].FlowMeasurementandInstrumentation, 2013, 33: 251-256.

[3] 王辉斌, 吴长利, 邹桂丽, 等. 水轮机故障声学诊断技术研究及其应用探讨[J].大电机技术, 2010(3): 45-50, 54.

WANG Huibin, WU Changli, ZOU Guili, et al. Acoustic fault diagnosis technology research and application in hydraulic turbine[J].LargeElectricMachineandHydraulicTurbine, 2010(3): 45-50, 54.

[4] RUS T, DULAR M,IROK B, et al. An Investigation of the relationship between acoustic emission, vibration, noise, and cavitation structures on a Kaplan turbine[J].JournalofFluidsEngineering, 2007, 129(9): 1112-1122.

[5] 张俊华, 张伟, 蒲中奇, 等. 轴流转桨式水轮机空化程度声信号辨识研究[J].中国电机工程学报, 2006, 26(8): 72-76.

ZHANG Junhua, ZHANG Wei, PU Zhongqi, et al. Research on the cavitation identification of Kaplan turbine using acoustic signals[J].ProceedingsoftheCSEE, 2006, 26(8): 72-76.

[6] HE Yongyong, LIU Yuan. Experimental research into time-frequency characteristics of cavitation noise using wavelet scalogram[J].AppliedAcoustics, 2011, 72(10): 721-731.

[7] SCHMIDT H, KIRSCHNER O, RIEDELBAUCH S. Cavitation measurements on a pump-turbine model[J].JournalofPhysics:ConferenceSeries, 2015, 656(1): 012071.

[8] SUN Hailiang, HE Zhengjia, ZI Yanyang, et al. Multiwavelet transform and its applications in mechanical fault diagnosis—a review[J].MechanicalSystemsandSignalProcessing, 2014, 43: 1-24.

[9] 卢绪祥, 苏一鸣, 吴家腾, 等. 基于EMD及灰色关联度的滑动轴承润滑状态故障诊断研究[J].动力工程学报, 2016, 36(1): 42-47.

LU Xuxiang, SU Yiming, WU Jiateng, et al. Fault diagnosis on lubrication state of journal bearings based on EMD and grey relational degree[J].JournalofChineseSocietyofPowerEngineering, 2016, 36(1): 42-47.

[10] LEI Yaguo, LIN Jing, HE Zhenjia, et al. A review on empirical mode decomposition in fault diagnosis of rotating machinery[J].MechanicalSystemsandSignalProcessing, 2013, 35: 108-126.

[11] 向玲, 杨世锡, 唐贵基, 等. 汽轮发电机组轴系扭振的时频特征分析[J].动力工程学报, 2011, 31(9): 649-654, 671.

XIANG Ling, YANG Shixi, TANG Guiji, et al. Time-frequency analysis on torsional vibration of turbo-generator shafts[J].JournalofChineseSocietyofPowerEngineering, 2011, 31(9): 649-654, 671.

[12] KEDADOUCHE M, THOMAS M, TAHAN A. A comparative study between empirical wavelet transforms and empirical mode decomposition methods: application to bearing defect diagnosis[J].MechanicalSystemsandSignalProcessing, 2016, 81: 88-107.

[13] 王国栋, 胡邦喜, 高立新, 等. 自适应小波降噪在轴承故障诊断中的应用[J].噪声与振动控制, 2007, 27(5): 100-103, 106.

WANG Guodong, HU Bangxi, GAO Lixin, et al. Application of adaptive wavelet denoising on bearing fault diagnosis[J].NoiseandVibrationControl, 2007, 27(5): 100-103, 106.

[14] 刘忠, 邹淑云, 陈莹, 等. 混流式水轮机模型空化状态与声发射信号特征关系试验[J].动力工程学报, 2016, 36(12): 1017-1022.

LIU Zhong, ZOU Shuyun, CHEN Ying, et al. Experiments on the relationship between cavitation status and acoustic emission signal features for a Francis turbine model[J].JournalofChineseSocietyofPowerEngineering, 2016, 36(12): 1017-1022.

[15] 李静, 周建中, 肖剑, 等. 基于小波包变换和关联维数的空化信号特征提取[J].水力发电, 2013, 39(10): 53-57.

LI Jing, ZHOU Jianzhong, XIAO Jian, et al. Feature extraction of turbine cavitation based on wavelet packet and fractal analysis[J].WaterPower, 2013, 39(10): 53-57.

[16] 刘忠, 邹淑云, 李志鹏, 等. 离心泵空化状态下声发射信号的小波能量特征[J].农业工程学报, 2015, 31(8): 99-103.

LIU Zhong, ZOU Shuyun, LI Zhipeng, et al. Wavelet energy features of acoustic emission signals under centrifugal pump cavitation conditions[J].TransactionsoftheChineseSocietyofAgriculturalEngineering, 2015, 31(8): 99-103.