合流调蓄系统多目标GA优化工程应用
陆松柳
(上海市政工程设计研究总院(集团)有限公司,上海市200092)
1 研究背景
在城市面源污染“源头-过程-末端”全过程控制过程中,径流削减、雨水截流、雨水调蓄,以及雨水末端排放处理等为关键环节。但我国许多老城区仍延用合流制排水系统,因客观因素的制约,无法彻底改造成分流系统,在雨天或融雪期条件下,容易发生合流制溢流(CSOs)进而污染城市受纳水体[1]。合流制排水系统中的截流倍数大小直接决定了雨水尤其是初期雨水带来的面源污染程度,也可有效地控制污水溢流。理论上提高截流倍数可控制溢流,但截流污水主干管管径和污水处理设施的雨季处理能力也要随之增大,投资也会随之提高;适当配置应用雨水调蓄池,可极大地降低雨水管道尺寸,降低工程造价。事实上,合流制排水系统涉及管道工程、提升泵站工程、调蓄池工程、污水处理厂工程等,是一个多参数、多因素、多目标的系统,需对其进行优化,尤其是截流规模(管网管径)与调蓄规模(调蓄池容积)的关系。优化过程需考虑当地排水能力和污染控制效果的同时,确保系统工程的最佳经济效益,然而利用传统手工计算方法难以较快、较准确地优化合流制排水系统。
针对上述问题,本文提出了一个合流制排水系统多目标优化模型,并将GA算法运用于该系统优化工程研究中,利用GA算法的内在并行机制及其全局优化的特性,且根据不同条件选取出最优的方案;同时,在多个欲实现的目标之间寻找出最佳的平衡关系,为工程评估和投资提供科学的依据与参考。
2 多目标与优化问题
现实中存在着较多的多目标问题,由于存在技术和计算方法的局限,往往对其简单化,即将多目标问题转化为单一目标进行求解。
2.1 多目标问题
无论是科学研究还是在工程应用上,多目标优化都是非常重要的研究课题[2]。给水排水工程和环境工程中均存在很多优化问题,如给水排水工程中的管网平面布置优化、管网参数优化、污水处理厂位置优化等;环境工程中的监测点优化、污染控制系统优化、污染排放风险优化、排放权优化等。在合流制调蓄系统中,除存在管道、泵站、调蓄池、污水处理厂布设及相关参数的优化问题外,在实际工程中,系统建设费用优化也是其备受关注的方面。
2.2 优化算法
2.2.1 Pareto最优解
由于在大多数情况下各目标可能相互冲突,某目标的改善可能引起其它目标性能的降低。经综合考虑相互冲突的子目标,对各子目标进行折衷和协调权衡处理,可实现总体任务的最优化。与单目标的优化不同,多目标优化问题通常有多个最优解,被称为Pareto最优解[3],由无优劣之分、相互冲突的优化目标所构成。在优化解的集合中,很难找到使得所有目标同时达到最优的绝对或唯一结论,故可根据设计者对各目标的偏好程度,择其最满意的解[4]。
2.2.2 GA算法
基于自然选择和GA理论,美国密歇根大学的John Holland教授于1975年创建了GA算法。它是一种结合达尔文生物进化论中适者生存原则与群体内部染色体信息随机交换机制的过程搜索Pareto最优解的算法,已在函数优化、生产调度、模式识别、神经网络、自适应控制等领域得到广泛应用[5]。
2.2.3 其他算法
将多目标削减至单目标可采用不同的技术途径,其中Zitzler在1999年提出的加权聚集法可根据不同目标的重要程度给出一组权重系数,将多目标向量转换成数量形式,因其计算量小,因而得到了较为广泛应用[6]。但对于目标函数数量大且搜索空间复杂的优化问题,加权聚集法仍会因其重现性差而表现出一定的局限性。距离函数法、最小-最大法、ε值约束法等也是求解Pareto最优解的运算方法。
采用传统优化算法需经多次运算才能获得一组近似Pareto最优解,而基于帕累托优势和非支配概念的多目标GA算法经一次运行就能得到更多的Pareto解[7],且不破坏任何一个目标函数的完整性。
3 多目标GA算法的实现
3.1 目标函数的建立
在合流制排水系统优化过程中,通常会根据设计者的不同要求而建立不同的目标函数。本文将对某地区合流制排水系统进行优化配置,建立以工程造价和运行费用为目标函数的模型。目标函数达到最小值时,以确定管网管径和调蓄池容积这两个关键因素。合流制溢流调蓄池的主要作用是截流初期雨水,提高合流制排水系统的截流倍数[8]。
合流制排水系统建设的工程费用主要包括传输管道、调蓄池、泵站和污水处理厂。鉴于设施整体生命周期评价,工程总费用又由三部分组成[8]:(1)基建费用;(2)系统在投资偿还期内的管理和维护费用;(3)设施服役结束时残余价值的现值。该研究算法程序中涉及的管道费用函数、调蓄池费用函数、泵站费用函数、污水处理厂费用函数如下所述。
3.1.1 管道费用函数
管道单位管长基建费函数如下:

式中:CC1为单位管长基建费,万元/m;D为管道直径,m;H为管道平均埋深,m;ki为系数,上海地区为 0.03、0.09、0.137、1.345、2.066。
管道运行费用函数如下:

式中:Co1为年运行费,万元/年,年限设为20年;p为年运行费相对基建费的综合费率,上海地区为0.0883;Co1为基建费,万元。
3.1.2 调蓄池费用函数
关于调蓄池基建费函数,根据经验大概估算如下:

式中:CC2为基建费,万元;V为调蓄池体积,m3;H为调蓄池深度,m;h为覆土深度,m;Z为固定费用,万元,取值200;ki为系数,上海地区为0.3、0.45、0.6。
3.1.3 泵站费用函数
污水泵站基建费函数如下:

式中:CC3为泵站基建费,万元;H为泵站扬程,m;Q为泵站流量,m3/s;ki为系数,上海地区为1 000、24.4、89.6。
污水泵站运行费用函数如下:

式中:Co3为泵站年运行费,万元/年;CC3为泵站基建费,万元;Q为泵站流量,m3/s;H为泵站扬程,m;E为泵站用电电费,元/度;p为年运行费占基建费的比例;k为电费占运行费的比重;ηp为泵的运行效率;ηm为电机效率。
3.1.4 污水处理厂费用函数
污水处理厂基建费函数如下:

式中:CC4为污水处理厂基建费,万元;Q为处理流量,m3/s;ki为系数,上海地区为 2 000、0.445 3。
污水处理厂运行费用函数如下:式中:Co4为泵站年运行费,万元/年;Q为处理流量,m3/s;BOD5为生化需氧量,mg/L;CODcr为化学需氧量,mg/L;SS为悬浮颗粒物,mg/L;TN为总氮量,mg/L;TP 为总磷量,mg/L;A 为运行年限,取 20 a;ki为系数,上海地区为 300、0.715、0、1.45、0、0.25、0.24、0、007。

3.2 约束条件
在进行优化计算的过程中除考虑目标外,还需考虑多方面的约束条件。本文中,约束条件主要包括基本约束、管网水力参数约束及假定约束。不发生溢流(Non-overflow)为计算过程中的基本约束条件。
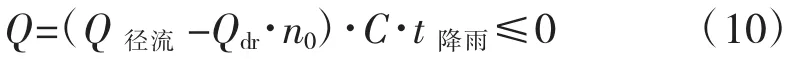
式中:Q为溢流量,m3/s;Q径流为径流设计流量,m3/s;Qdr为旱季污水量,m3/s;n0为截流倍数;C 为污染物浓度,mg/m3;t降雨为降雨历时,s。
其他管网水力条件均作为约束条件,遵守管网计算规范和原则。例如,根据《室外排水设计规范》GB50014-2006(2016年版)[9]和《给水排水设计手册》[10],非金属管道最大设计流速为5 m/s,合流管道在满流时最小设计流速为0.75 m/s;管径需参考国家设计规范以及市售管径范围合理取值。

式中:D为市售可选管径集合。
此外,假定有多个溢流井,认为各个流域共享一场降雨,即同时降雨和同时终止降雨,并按照此条件约束设计。
3.3 计算步骤
合流调蓄系统多目标优化实现方法以GA算法为基础,实现方法的具体流程如下所述。
3.3.1 初始化
随机生成第一代种群P0,即调蓄池池容和管网管径,种群由n个个体组成,每个个体代表一种调蓄池的布置方案,即一组调蓄池节点模型的面积参数数组,当面积参数为0时,相当于该节点处不设调蓄池。通过选择、交叉和变异随机生成数量为1 000的子代Q0,将父代P0与子代Q0合并成数量为2n的种群R0。
3.3.2 计算目标函数
计算种群R0当中每个个体的目标函数,即管网、泵站、调蓄池、污水厂的工程总造价和运行总费用。通过水力计算判断是否满足不溢流、管网水力等约束条件。
3.3.3 非支配优选
根据各个个体的目标函数数值和是否破坏约束条件进行非支配排序,其中破坏约束条件的个体将被任一不发生溢流的个体所支配。按非支配等级从高到低挑选个体直到个体数超过N,最后在一个非支配等级的个体挑选中,拥挤距离大的个体将被优先选择。N个被选择的个体组成第二代父代种群P1。
3.3.4 循环
父代P1通过选择、交叉和变异产生Q1,P1与Q1组成R1后重复第2步和第3步的过程生成P2。不断循环至满足优化准则为止,便可生成第t代群体Pt。种群Pt即为合流调蓄多目标优化的Pareto最优解。
4 实例分析
上海市杨浦区四平排水系统(见图1),其服务范围为北起国定路北,南至走马塘,西起邯郸路西,东至黄兴路东,服务总面积2.05 km2。系统设计标准为设计暴雨重现期1 a,径流系数0.6。排水体制为合流制,排水模式为强排,目前已有3座调蓄池。四平泵站位于四平路西侧、走马塘以北,雨水经泵站提升后进走马塘,泵站设计规模为14.0 m3/s。
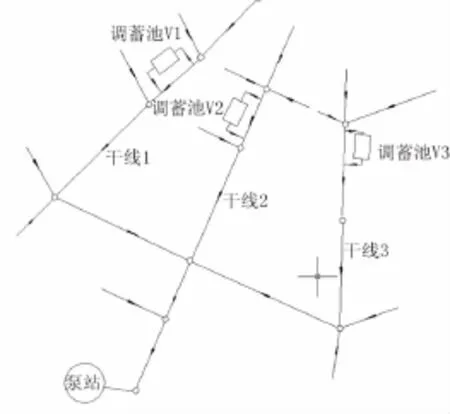
图1 上海市杨浦区四平排水系统示意图
新建模型的参数包括:人均流量200 L/d、人口密度 350 人 /hm2、COD 350 mg/L、BOD 150 mg/L、SS 250 mg/L、TN 45 mg/L和氨氮35 mg/L。现有该地区降雨资料和现状雨水管网分布等基础资料,通过新建模型优化计算,获得在“某降雨强度下系统不发生溢流”条件下,最优方案(对应管道+调蓄池+泵站的总费用最低)时的截流管径与调蓄池容积。
调蓄池数量为3座,起点溢流井埋深为4 m,0.5 a一遇 2 h(前锋、后锋)、3 a一遇 2 h(前锋、后锋)降雨强度下,进行该排水系统的多目标优化运算。考虑实际情况,该项研究将工程造价和运行费用视为最优解的决策因子。该区排水系统优化计算结果如表1所列。

表1 不同降雨条件下合流调蓄优化结果一览表
从多目标GA算法计算结果来看,不同雨型条件下,管道+调蓄池+泵站的总费用最小值明显不同,所对应的最佳的截流管径与调蓄池容积设计值也不同。3 a一遇雨型条件下,系统工程总费用最小值明显高于0.5 a一遇雨型,这一计算结果与实际工程建设相符。
为更好地应用该项研究设计的多目标优化模型,本文还对模型进行了多调蓄池单因子条件下灵敏度分析,即在管网节点地面标高、旱流量等参数不变的条件下,改变管道长度或控制埋深(参数以20%幅度增加)时,含3座调蓄池的排水系统总费用变化情况如图2所示。

图2 管道长度、节点控制埋深对模型灵敏度的影响曲线图
模型运算结果显示(见图2),合流排水系统(含3座调蓄池)中,随着管道长度的逐渐增加,工程总费用明显增加,当管道长度增加至原管长度的140%倍时,总费用已达195 356.57万元。随着管道埋深的增加,总造价呈缓慢增加趋势,且管道埋深对工程总费用的影响远小于管道长度(见图2)。以上模型运算结果同样与实际经验相符。
5 结语
合流制调蓄设计与优化是城市雨水面源污染控制的重要内容,由于排水系统具有多目标性,所以利用传统手工计算方法难以较好地解决此类问题。本文提出了GA算法在合流制排水系统多目标优化工程中的应用。通过构建以工程造价和运行费用为目标函数,以不发生溢流为基本约束、管网相关水力为其他约束条件的合流制排水系统多目标优化模型,在不同的降雨条件下,利用GA算法寻求最优的工程设计方案,且该模型具有良好的灵敏度。将模型应用于工程实例中,由实例计算求解出的优化结果合理、可行,对合流调蓄系统评估和规划具有现实和推广意义。为进一步促进优化设计在工程实践中的应用,在后续模型研究中,可结合Infoworks二次开发分析本模型的敏感性,深入解析模型各环节对模型目标实施的影响作用。
[1]张善发.合流制排水系统雨天溢流污染防治技术研究 [D].上海:同济大学,2006.
[2]郑金华.多目标进化算法及其应用(精)[M].北京:科学出版社,2007.
[3]蒋怀德.给水管网多目标优化设计 [D].上海:同济大学,2007.
[4]陈南祥,李跃鹏,徐晨光.基于多目标遗传算法的水资源优化配置 [J].水利学报,2006,37(3):308-313.
[5]罗述全.传统优化算法与遗传算法的比较 [J].湖北工业大学学报,2007,22(3):32-35.
[6]Zitzler E.Evolutionary algorithms for multi-objective optimization:methods and applications [D].Swiss Federal Institute ofTechnology,1999.
[7]赖红松,董品杰,祝国瑞.求解多目标规划问题的Pareto多目标遗传算法 [J].系统工程,2003,21(5):24-28.
[8]乔纳森·帕金森,奥尔·马克.发展中国家城市雨洪管理 [M].北京:中国建筑工业出版社,2007.
[9]GB50014-2006,室外排水设计规范[S].
[10]北京市政设计院.简明给水排水设计手册 [M].北京:中国建筑工业出版社,1992.

