基于气动驱动的多级伸缩杆系统设计
□ 高宏伟 □ 刘积宏 □ 林科禄
西安电子科技大学机电工程学院 西安 710071
1 研究背景
所谓伸缩机构,是指总长度能够沿着某个直线方向发生伸展或收缩的一种机构。按照驱动介质的不同,可以将伸缩机构分为液压驱动伸缩机构、旋转伸缩机构及平行四边形铰接伸缩机构等[1]。
气压传动技术以压缩空气为工作介质和动力源,实现能量或信号传递。气动技术不但在尖端的科研技术领域得到一定应用[2-3],而且也进入了微电子、农林、生物技术等领域[4-5],正发挥着越来越重要的作用。
气动技术的应用历史悠久,但是目前针对气动式伸缩机构的研究却较少。气动驱动伸缩机构基本原理与液压驱动伸缩机构相似,但液压传动工作稳定性较差,噪声较大,且还要考虑密封问题,因此在较大结构的伸缩机构上应用较少。
相比电气传动、液压传动及机械传动,气压传动具有以下优点[6]:① 工作介质为压缩空气,容易获得,使用之后可以排放至大气中,处理方便,与液压传动相比,不需要设计回油装置;② 与液压传动相比,气压传动反应速度快,维护简单,工作介质清洁;③环境适应性好,尤其适用于多粉尘、易燃、易爆、强磁及振动等条件恶劣的环境中,外泄漏不会发生环境污染,适合在食品、纺织、印刷、轻工及精密检测等行业中使用。
笔者基于气动驱动设计了一套多级伸缩杆系统,这一系统的伸缩杆展开长度约3.5 m,回收后长度约0.35 m,可将约1.5 kg质量的载荷在1~2 s内推送出去,在10 s内回收。
2 系统设计
多级伸缩杆系统工作原理如图1所示,包括伸缩筒、固定筒、牵引钢丝绳、牵引辊、控制阀、气缸及气泵等。

▲图1 多级伸缩杆系统工作原理图
当伸缩杆工作时,直流充气泵向气缸输入气体。气缸内产生一定的压力后,关闭气泵,打开气缸与伸缩杆间的控制阀,使气缸内的气体进入伸缩杆,以此来驱动伸缩杆伸展。可见,伸缩杆的伸展过程实质就是气缸放气过程。当伸缩杆结束工作之后,通过回收系统将伸缩杆收回。采用回收系统时,启动电机,带动齿轮及离合器工作,通过钢丝绳实现伸缩杆回收。钢丝绳一端固定在牵引辊上,另一端固定在第13节伸缩筒的尾端。
3 伸缩杆系统建模与放气时间计算
将图1所示多级伸缩杆系统简化为等效模型,如图2所示。
不工作时气缸内气体的状态参数包括气缸内腔气体体积Va、气缸内气体质量M1、气缸内气体初始温度T1、气缸内气体初始压强p1。工作时气缸内气体的状态参数相应变为Ma、Ta、pa,伸缩杆内气体的状态参数相应为 Vb、Mb、Tb、pb。 控制阀截口的有效面积为 Au。
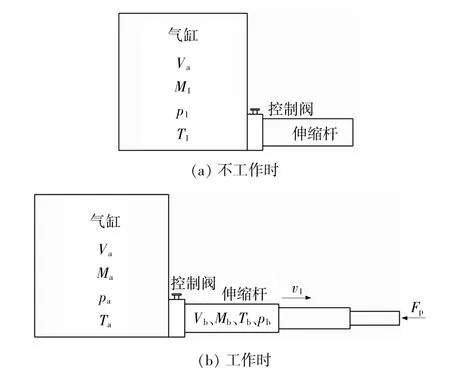
▲图2 多级伸缩杆系统等效模型
进行如下假设[7]:① 气体为理想气体,大气压为p;②气缸、伸缩杆与外界没有气体泄漏;③ 气体流过控制阀截口的流动是稳定的一元流动;④气缸的排气过程是一个等熵过程,即气体与外界的热交换可以忽略。
根据热力学第一定律,可得:

式中:dQ为系统内气体通过容器壁与外界交换的热量;i1为从气源流进系统1 kg气体所带进的能量,即气源气体的比焓;dM1为从气源流进系统的气体质量;dU为系统内气体的内能变量;dW为系统内气体所作的膨胀功,包括伸缩杆的动能及摩擦力所作的功;i为流失1 kg气体所带走的能量,即流失气体的比焓;dM为同一时间内从气缸流出的气体质量。
根据气缸工作过程中容腔的气体压强变化特性,同时考虑到伸缩杆系统内的气压远远大于外界大气压,因此可忽略外界气压及每节伸缩杆间的摩擦力影响,将系统简化为如图3所示模型。
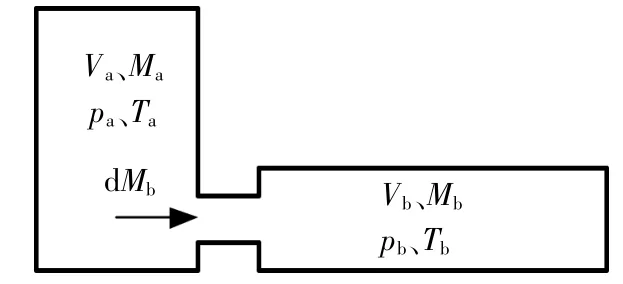
▲图3 多级伸缩杆系统进一步简化模型
气缸只放气不充气,则有 dQ=0,dM1=0,内能为:

式中:cV为定容比热;cp为定压比热,cp与cV满足cpcV=R,cp/cV=k,R为气体常数,k为气体比热比。
容积膨胀功为:

气缸内气体流出带走的能量为:

将式(2)~式(4)代入式(1),得:
将 cV=R/(k-1)、dMa=-dMa、paVa/Ma=RTa代 入 式(5),化简得:

则气缸内气体的流量方程为:
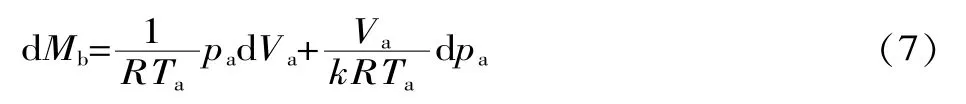
由此可以得到气缸的压强变化方程为:

由于Qm=dMb/dt,Qm为筒内气体质量随时间的变化值,求导得:

同理可得伸缩杆的压强变化方程为:

由于放气过程较快,气缸与伸缩杆内的气体来不及与外界进行热交换,因此可以看作绝热过程,气体的温度变化为:

设图3中伸缩杆的最左端为坐标原点,则气缸与伸缩杆的体积变化为:

由此可得气缸的排气方程为:
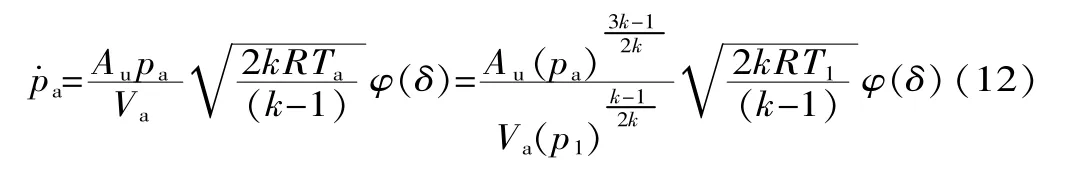
伸缩杆的充气方程为:

气缸放气的仿真参数如下:气缸体积为5.4×10-3m3,放气口直径为6 mm,气缸初始压强为490 kPa,大气压强为101.3 kPa,气缸初始温度为291 K,伸缩杆等效直径为50 mm,伸缩杆质量为3 kg,气体常数为287.1 J/(kg·K),气体比热比为1.4。 将各参数代入式(12)、式(13),利用MATLAB软件得到如图4所示两条曲线。
由图4可以看出,气缸内压强和伸缩杆内压强在1.33 s后趋于稳定,说明伸缩杆的放气理论时间为1.33 s,即伸缩杆完成伸展过程需要1.33 s。
4 伸缩杆伸展过程数值模拟
4.1 模拟假设
气缸放气过程中所涉及的动力学及热力学问题十分复杂,对气缸放气过程进行完全数学模拟是十分困难的。因此,为了能够顺利对气缸放气过程进行仿真,做了一些基本假设:①气体是理想气体;②在气缸放气过程中,气缸及伸缩杆中的气体和外界不进行热量交换;③设定气缸与伸缩杆内壁温度保持不变,始终为18℃。
4.2 几何建模
鉴于气缸与伸缩杆均为轴对称结构,建立如图5所示的整个多级伸缩杆系统几何模型。

▲图4 MATLAB仿真曲线

▲图5 多级伸缩杆系统几何模型
4.3 仿真结果
排气口处质量流量变化曲线如图6所示。

▲图6 排气口处质量流量变化曲线
由图6可以看出,排气口处的质量流量伴随放气时间的延长而不断减小。在数值模拟开始阶段,质量流量的变化梯度很大。伴随着气缸内部气体逐渐减少,质量流量的变化梯度也逐渐变小。在气缸放气刚开始时,排气口处的质量流量大约为25.1 g/s。放气到1.8 s时,排气口处的质量流量大约为0.2 g/s。之后,质量流量接近于0,说明伸缩杆伸展过程模拟时间为1.81 s。
5 伸缩杆最大变形分析
多级伸缩杆系统应用的对象主要是车辆,不平的路面对车辆产生的振动会对伸缩杆的性能产生影响。通过构建伸缩杆模型,将路面不平度的随机激励作为输入激励,对振动响应进行分析,得出伸缩杆性能所受的影响,并对伸缩杆结构进行优化。
5.1 车辆振动模型
车辆的振动主要是竖直方向的振动,由路面不平度与车辆悬挂系统之间相互作用所引起。此外,车辆还会产生横向振动,主要来自于侧甲板等附件的激励,如主动轮、托带轮、诱导轮等[8]。
如图7所示,设车辆的行驶速度为v,取车辆静平衡位置时的质心作为动坐标原点,z′表示车辆质心相对于静平衡位置的竖直位移,zi表示各个负重轮的竖直位移[9]。

▲图7 车辆线性振动力学模型简图
假设车辆在路面激励位移 q={q1,q2,…,qn}的作用下,车辆的惯性矩为I,振动为z,那么车辆行驶时的动力学方程为:

式中:Cab=M-1C/(2ξzωz),Kab=M-1K/ωz2,M、C、K 依次为示系统的质量矩阵、阻尼矩阵及刚度矩阵;am、ak分别为质量比和刚度;ξz为车体竖直线振动的阻尼比;ωz为车体竖直线振动的固有频率。
车辆在路面上行驶时,激励q的元素就是车速v的函数,所以车辆的振动z取决于阻尼比ξz、固有频率ωz与车速v,在激励频率和车体固有频率逐渐接近时,车体的振动会越来越剧烈。
5.2 伸缩杆最大变形计算
当伸缩杆处于全展开状态时,伸缩杆第13节伸缩筒的末端变形最大,所以必须计算伸缩杆的末端变形量。笔者采用当量惯性矩法,不考虑伸缩杆之间的间隙与加工误差,计算伸缩杆末端的变形[10]。当量惯性矩法将变截面的伸缩杆转化为刚度相当的等截面伸缩杆来计算末端的变形,公式为:

式中:f为最大变形;Id为伸缩杆等截面当量惯性矩;E为材料弹性模量;L为伸缩杆长度;T′为等效至伸缩杆末端的横向力;M′为等效至伸缩杆末端的弯矩。
伸缩杆最大变形计算模型如图8所示。
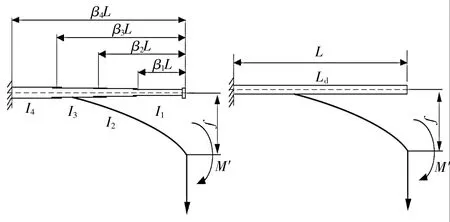
▲图8 伸缩杆最大变形计算模型
根据刚度相等条件,可得等截面当量惯性矩Id为:

式中:βi为第i节伸缩筒到第i+1节伸缩筒搭接处1/2的距离,Ii为第i节伸缩筒的截面惯性矩。
伸缩杆最大变形的仿真参数如下:弹性模量为230 GPa,伸缩杆长度为3 527 mm,伸缩杆端部配重为1.5 kg。伸缩杆各节伸缩筒的尺寸参数可参考文献[11]中表 2.1。将伸缩杆参数代入式(15)、式(16),求得伸缩杆的最大变形为50 mm。
5.3 伸缩杆建模
利用ANSYS Workbench软件自带的建模功能建立伸缩杆模型,如图9所示。其中第6节伸缩筒模型如图10所示。

▲图9 伸缩杆模型

▲图10 伸缩杆第6节伸缩筒模型
伸缩杆所使用的材料为碳纤维,前止环1、前止环2及后限位套所使用的材料为聚甲醛,具体的材料属性见表1。

表1 伸缩杆材料属性
伸缩杆第1节伸缩筒固定在支架上,伸缩杆除受到自身质量(1.784 kg)的作用外,在第13节伸缩筒处还受到1.5 kg外载荷质量块的作用。为了简化模型,直接将质量块的重力施加到伸缩杆上,如图11所示。

▲图11 伸缩杆模型外载荷
5.4 静力仿真
伸缩杆模型在受到自身及质量块重力作用下的变形与应力云图如图12所示。

▲图12 伸缩杆模型静力仿真结果
由图12可知,伸缩杆模型在受到自身和质量块重力作用下的最大变形为42.59 mm,位于第13节伸缩筒末端;伸缩杆模型的最大应力为68.352 MPa,小于材料的许用应力,满足强度要求;大应力主要分布在第8至第13节伸缩筒,前7节伸缩筒的应力比较小。
5.5 随机振动仿真
多级伸缩杆系统在车辆上使用,车辆的不平工作路面大致可分为碎石路面、铺面路面及起伏路面。选取这三种不平路面,并选取车速20 km/h、30 km/h、40 km/h作为研究工况,对伸缩杆进行随机振动分析。
根据仿真结果绘制曲线图,得到不同工况下伸缩杆Z轴方向的位移变形曲线和等效应力曲线,如图13所示。

▲图13 伸缩杆模型随机振动仿真结果
由图13(a)可知,随着车速的加快,伸缩杆Z轴方向上的位移变形也随之增大;车辆在起伏路面上行驶时,伸缩杆的位移变形要大于其它两种路面;当车辆速度为40 km/h时,最大变形量为33.378 mm,位于伸缩杆第13节伸缩筒的末端。伸缩杆最大变形量小于静力下的变形量,原因是车辆行驶过程中,随机振动在伸缩杆固有频率所对应的功率谱密度较小,不可能使伸缩杆发生共振。
由图13(b)可知,随着车速的加快,伸缩杆等效应力也随之增大;起伏路面下的等效应力要大于其它两种路面,最大等效应力为61.06 MPa,小于许用应力,满足强度要求。
6 伸缩杆结构优化
应用ANSYS Workbench软件自带的建模功能进行参数化建模,验证所建立的伸缩杆模型是否合理,并进行结构优化。
6.1 参数定义
伸缩杆结构优化设计的目的是保证伸缩杆在Z轴方向上的下垂量不大于理论计算值 (50 mm)的情况下,使伸缩杆质量达到最轻化,所以其目标函数可设为:

式中:G(X)为质量与设计变量 X 的关系式;f(x1,x2,…,xn)为伸缩杆在Z轴方向上的下垂量。
将伸缩杆第1节伸缩筒的后限位套长度作为设计变量,即输入参数。由于伸缩杆模型所涉及到的构件多达49个,为了减小计算量,在参数化建模时对模型尺寸进行处理:

式中:x为优化后第1节伸缩筒的后限位套长度;yi、zi、di依次为优化后第2至第7节伸缩筒前止环2、后限位套以及伸缩筒自身的长度;Yi、Zi、Di依次为优化前第2至第7节伸缩筒前止环2、后限位套及伸缩筒自身的长度。

式中:y8、z8、d8依次为优化后第 8 节伸缩筒前止环 2、后限位套及伸缩筒自身的长度;Y8、Z8、D8依次为优化前第8节伸缩筒前止环2、后限位套及伸缩筒自身的长度。

式中:yi、di分别为优化后第9至第13节伸缩筒前止环2及伸缩筒自身的长度;zi为优化后第9至第12节伸缩筒后限位套的长度;Yi、Di分别为优化前第9至第13节伸缩筒前止环2及伸缩筒自身的长度;Zi为优化前第9至第12节伸缩筒后限位套的长度。
经过理论分析和数次试算,定义设计变量的范围为12~20 mm。选取伸缩杆的最大变形量与质量作为输出参数。
6.2 优化结果
经过ANSYS软件优化,得到第1节伸缩筒后限位套长度与最大变形量关系,如图14所示。

▲图14 第1节伸缩筒后限位套长度与最大变形量关系
由图14可见,当伸缩杆的最大变形量为50 mm时,第1节伸缩筒后限位套长度为12.88 mm,此时伸缩杆的总质量为1.571 7 kg,比优化前减轻了0.212 3 kg。优化前后各节伸缩筒的尺寸对比参考文献[11]表6.1。
图15为优化前后第2节伸缩筒的尺寸变化。
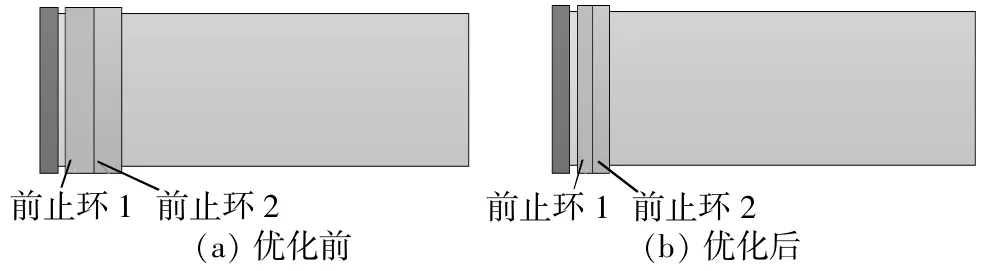
▲图15 优化前后第2节伸缩筒尺寸变化
6.3 优化后数值模拟
优化前后静力时伸缩杆最大变形量与最大应力见表2。优化后伸缩杆最大变形量为49.941 mm,小于50 mm,位于第13节伸缩筒末端,最大应力为73.041 MPa,小于许用应力,满足强度要求。
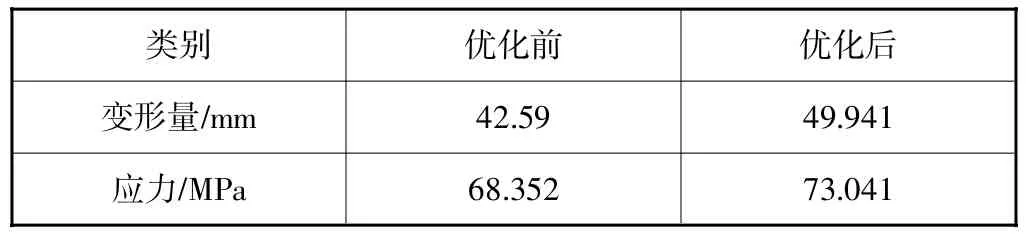
表2 优化前后静力时伸缩杆最大变形量与最大应力
在车速为40 km/h时,伸缩杆位移变形与等效应力最大,因此此处取三种不同路况,车速为40 km/h进行分析,结果见表3。

表3 优化前后伸缩杆随机振动最大变形量与最大应力
由表3可见,优化后不同路面下伸缩杆最大位移变形量比优化前减小,其中以铺面路面的位移变形量减小得最多;优化后不同路面下伸缩杆最大应力也比优化前减小,且全都满足强度要求。所以,经过优化设计,伸缩杆不仅在质量上有所减轻,而且性能上也有所增强。
7 性能测试
伸缩杆性能测试系统主要包括伸缩杆、质量块、气缸、电机、齿轮和离合器等部分,如图16所示。

▲图16 伸缩杆性能测试系统
空气压缩源由24 V小型直流充气泵提供动力,最大充气压力为8 kg/cm2。气缸外径为152 mm,长度为320 mm,壁厚为2.5 mm,容量为6.5 L,工作压力大于1 MPa,材质为20号钢。伸缩杆采用套筒式结构,由1节固定伸缩筒和12节活动伸缩筒组成。固定伸缩筒采用7075-T6高强度铝合金制造,活动伸缩筒主要材料为T300碳纤维。
7.1 放气时间
通过测试得到伸缩杆的放气时间为1.6 s。
放气时间理论值、数值模拟值及测试值对比见表4。

表4 放气时间对比 s
由表4可见,三个放气时间相差很小,介于0.2~0.3 s之间。三个放气时间存在差别分析如下:在理论计算时,伸缩杆内的气压设为0,而在数值模拟时,伸缩杆内的气压设为一个大气压,如果测试时间介于理论时间和数值模拟时间之间,则可以论证理论分析与数值模拟基本上与实际情况相符,是可行的;此外,在理论分析与数值模拟时,鉴于多级伸缩杆系统是应用于实际工程中的,因此并未对放气过程中的一些细节问题进行讨论,如气路接头、容器密闭性等,在一定程度上也会对放气时间产生影响。
7.2 最大变形
通过测试得到伸缩杆的最大变形量为214 mm,出现在第13节伸缩筒的末端。
伸缩杆最大变形量的理论值、优化前后数值模拟值及测试值对比见表5。

表5 伸缩杆最大变形量对比 mm
由表5可见,伸缩杆最大变形的理论计算值与优化前后模拟值很接近,但与实际值有较大差距,主要原因分析如下:伸缩杆前止环与上一节伸缩筒内壁之间存在着0.03~0.08 mm的间隙,再加上加工误差,在自身和质量块重力作用下可导致最大变形量达到200 mm以上,而在建模时不考虑这些间隙与加工误差,前止环与上一节伸缩筒内壁之间的配合间隙假设为0。
8 总结
针对伸缩杆机构中电气传动、液压传动和机械传动的缺点,以及气压传动不能广泛应用于大型伸缩杆结构中的问题,设计了一种基于气动驱动的多级伸缩杆系统。建立了伸缩杆系统的数学模型和等效实体模型,分别应用MATLAB和计算流体动力学软件对伸缩杆的展开过程进行数值模拟和仿真分析,并与测试结果进行对比。建立伸缩杆三维模型,推导出伸缩杆的最大变形量数学公式,分别应用MATLAB和ANSYS软件对伸缩杆的最大变形量进行理论值计算和仿真分析,并与测试结果进行对比。应用ANSYS软件分析随机振动时伸缩杆的应力和变形,并进行结构优化。通过研究得到以下结论:①放气时间的理论值、数值模拟值及测试值相差很小,介于0.2~0.3 s之间;② 伸缩杆的最大变形量理论值与优化前后数值模拟值很接近;③起伏路面对伸缩杆振动的影响最大,车速越大,对伸缩杆的影响也就越大;④最大位移变形出现在伸缩杆第13节伸缩筒的末端,当车辆以40 km/h的速度在起伏路面上行驶时,伸缩杆的变形量最大,为33.378 mm;⑤最大等效应力主要分布在伸缩杆的第8至第13节伸缩筒,当车辆以40km/h的速度在起伏路面上行驶时,伸缩杆的等效应力最大,为61.06 MPa;⑥ 结构优化后伸缩杆质量减轻了12%,虽然优化后伸缩杆在静力时由自身重力及外载荷引起的变形与最大应力有所增大,但是通过随机振动分析,可以发现优化后伸缩杆结构的变形及最大应力均比优化前有所减小,可见优化后伸缩杆不仅在质量上有所减轻,而且在性能上有所增强。
[1]吴义成.伸缩机构的研究与设计[J].机电工程技术,2013,42(9):115-117.
[2]AUGE B K,LALLAS C D,PIETROW P K,et al.In Vitro Comparison of Standard Ultrasound and Pneumatic Lithotrities with a New Combination Intracorporeal Lithotripsy Device [J].Urology,2002,60(1):28-32.
[3]KAPOOR C,TESAR D.Integrated Teleoperation and Automation for Nuclear Facility Cleanup [J].Industrial Robot,2006(33):469-484.
[4]H IER C K,SONNENBORG T O,JENSEN K H.et al.Experimental Investigation of Pneumatic Soil Vapor Extraction [J].Journal of Contaminant Hydrology, 2007,89(1-2):29-47.
[5]赵彤.气动技术的发展及在新领域中的应用[J].液压气动与密封,2004(2):1-5.
[6]SMC(中国)有限公司.现代实用气动技术[M].2版.北京:机械工业出版社,2004:56-64.
[7]谢汉龙,赵新宇,张炯明.ANSYS CFX流体分析及仿真[M].北京:电子工业出版社,2012:1-7.
[8]贾进峰,张进秋,张建,等.基于路面谱随机激励的履带车辆舒适性仿真研究[J].系统仿真学报,2012,24(6):1350-1354.
[9]黄晋英,潘宏侠,张小强,等.履带车辆振动谱测试与分析方法研究[J].振动、测试与诊断,2009,29(4):457-461,480-481.
[10]陈士桐,张志起,王孝国.箱型伸缩臂的挠度计算[J].建设机械技术与管理,2013(2):114-118.
[11]林科禄.基于气动驱动多级伸缩杆系统设计[D].西安:西安电子科技大学,2014.

