高渗透率风电接入下地区高压电网转供模型
宁世超,吕 林,刘友波,许立雄,袁 川,杜新伟
(1. 四川大学 电气信息学院,四川 成都 610065;2. 国网四川省电力公司,四川 成都 610041)
0 引言
国家能源局在2011年发布国能新能[2011]226号《关于分散式接入风电开发的通知》和国能新能[2011]374号《关于印发分散式接入风电项目开发建设指导意见的通知》后,中等规模风电直接并入地区电网进行就地消纳的技术快速发展。受风能资源限制,加之本身所具有的随机性和波动性[1-2],风电接入呈现不均匀性,易导致地区电网局部消纳困难。同时,由于地区电网建设难以保证对各局部负荷增长的适应性,使其全局把控能力不足。因此,高渗透率地区高压电网易出现阻塞风险与消纳困境并存的情况。
针对风电非均匀接入导致的消纳困境,文献[3]从消纳能力和消纳水平两方面分析了其成因及危害,并提出了长期性建议。文献[4]提出了限制风电出力方法,虽提高了风电消纳能力,但也在一定程度上出现了“弃风”现象。而地区高压电网环网与辐射状网络并存,利用高度灵活可转供特点实现功率的均衡分布。但现有针对分布式电源DG(Distributed Generation)在配电网进行转供操作的研究,主要集中于10kV中压层面[5-6]。而对于高压电网的研究主要侧重于单一层面,如文献[7]基于高压配电网拓扑重构能力,推导了开、合环引起目标函数变化量的估算公式,在不计及DG的情况下分析网络重构对地区电网110kV网络的影响;文献[8]针对DG的随机波动性,建立了DG出力和负荷需求的动态概率模型,提出了地区电网动态概率潮流计算方法。同时,现有研究缺乏考虑DG的地区高压电网模型。文献[9]针对高压配电网典型接线模式提出了110kV变电站的配置判据;文献[10]进一步构建了基于高压电网灵活可转供特点的公共信息聚合模型(CIM);在此基础上,文献[11]针对现有模型对负荷重载问题解决效果欠佳的问题,提出了基于变电单元的高压配电网阻塞管控模型,但未考虑接入DG后的影响。由此可见,对于风电非均匀接入后的高渗透率地区高压电网,现有技术与模型难以兼顾其消纳困难和负荷重载两重问题。
同时,风电的随机性导致确定性条件下的转供算法并不完全适用,而机会约束规划是解决随机性问题的有效方法。机会约束规划是在一定置信水平下对随机变量进行决策,用概率性的思想求解系统随机性问题,并取得了良好的效果[12-13]。文献[13]考虑风机出力的不确定性,采用机会约束规划对配电网进行重构,取得了良好的效果。
综上所述,现有研究缺乏对中等规模风电非均匀接入后,高渗透率地区高压电网的模型以及运行优化技术。本文基于高压配电网的拓扑重构能力对110kV网络进行拓扑抽取,提出以变电单元为控制对象的高压配电网机会约束转供模型;针对风电的随机性和负荷的波动性,利用风电-负荷误差的概率密度函数对随机变量进行多状态建模;以源荷功率均衡分布为目标,综合考虑断路器动作次数和可控DG功率调整,构建不确定性条件下以拓扑重构为手段的地区高压电网运行优化技术;最后采用改进十进制遗传算法对模型进行求解。实际算例测试表明,本文所提方法对于高渗透率地区高压电网的阻塞困境与消纳矛盾有较好的均衡作用,并提高了设备利用率、消除了运行风险。
1 地区高压电网拓扑分析
1.1 拓扑结构表达和变电单元组
基于高压配电网的拓扑重构能力,本文提出以110kV变电单元为控制对象的高压配电网机会约束转供模型。高压配电网的转供操作是通过改变各变电单元间的连接关系实现,因此模型首先应明确变电单元含义及变电单元之间的连接关系。110kV变电站站内通常配有2~3台两卷变压器,根据《城市电力网规划设计导则》[14]规定,一般为单母分段、内桥及其与线变组的T接组合,如图1所示。
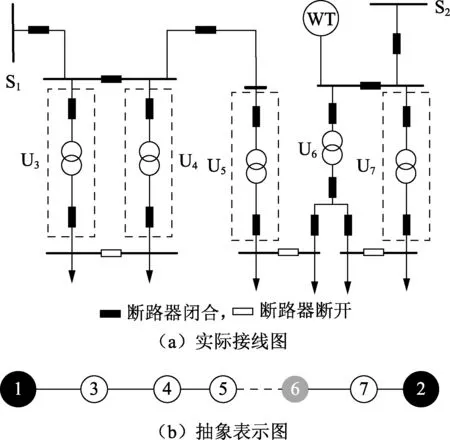
图1 变电单元及其连接关系Fig.1 Transformer units and their connected relations
图1(a)中,S表示220kV变电站,与图1(b)中黑色圆点对应;虚线方框内为110kV变电单元U,与图1(b)中白色圆点对应;WT表示风电,与图1(b) 中灰色圆点对应。图1(b)中虚线表示处于备供状态的110kV线路。
为了保证供电可靠性,地区高压电网110kV网络按环网设计标准建设有大量备供线路,最长备供距离可达10km,考虑每座110kV变电站至少存在1条备供线路,地区电网高压电网拓扑结构如图2所示。

图2 高压电网拓扑结构Fig.2 Topological structure of high-voltage network
由于建设有备供线路,110kV变电站与220kV变电站间存在多条可连通路径,110kV网络在保持开环运行的同时,潜在的网架结构极其丰富,为转供操作提供多种可能。
根据文献[11]所提变电单元组思想,按以下规则将图2(a)中各变电单元分为A1、A2、An:
a. 任意2个有电气连接的变电单元,如果此连接关系上没有220kV变电站,则它们及其之间的所有变电单元属于同一变电单元组;
b. 由固定220kV变电站向该单元组供电,这些变电站与该单元组中某一变电单元有直接电气联系(不经过其他组内单元);
c. 220kV变电站可向多个单元组同时供电,其负载大小等于此时所带变电单元的功率。
1.2 变电单元组可行拓扑状态的改进搜索算法
变电单元转供操作是通过改变110kV网络拓扑状态实现的,亦是改变110kV线路断路器的状态,若将全部状态代入求解算法,将会产生大量不可行解影响计算效率。同时,由于文献[11]中搜索算法缺乏对风电的考虑,本文提出适用于计及风电的地区高压配电网的可行拓扑状态的改进搜索算法。其具有以下2个特征:
a. 单元组内拓扑结构呈放射状,即单元组内任一变电单元最多与一座220kV变电站有通路;
b. 单元组内无孤岛存在,即单元组内任一变电单元最少与一座220kV变电站有通路。
以图2(a)中An为例,阐述高压配电网可行拓扑状态φn的获取方法。An内有β个变电单元(BUni={U1,U2,…,Uβ}),由γ座220kV变电站(BSub={S1,S2,…,Sγ})向其供电,有m个可操作断路器(BBre={QF1,QF2,…,QFm}),用0(断开)和1(闭合)表示断路器状态,生成所有可能拓扑状态集合φn,0(φn,0={x1,x2,…,xn}),共2m种可能的拓扑状态。根据高压配电网转供操作的特点,提出适用于本文的逻辑约束条件:
a. 任意转供操作中断路器动作需配套出现,即闭合状态断路器数量恒定;
b. 对于转供过程中具有多座220kV变电站选择情况,只能选择其中一个转供方向。
将上述条件通过数学表达如式(1)所示,满足条件的拓扑状态集合φn,1即可满足特征式(1)。
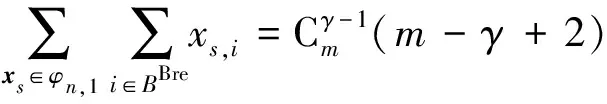
(1)
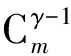
根据An的拓扑结构生成表示其节点(包括220kV变电站节点和变电单元节点)的矩阵Gn(m×1)及其连接关系的矩阵Bn(m×2);从φn,1中取xs与矩阵Bn构成表示网络状态的矩阵Bn(xs)(m×3),如式(2)所示。
(2)
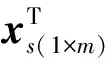
以220kV变电站节点为搜索起点,根据Bn(xs)中断路器状态遍历节点,在Gn(m×1)中将经过的节点置1、未经过的节点置0得到Gn(xs)(m×2)。由于φn的可行拓扑状态均需满足特征b,因此Gn(m×2)的第二列需满足:

(3)
得到An的所有可行拓扑状态φn之后,可以形成γ×β阶220kV变电站所带负荷矩阵Ssu,其元素Ssu(i,j)表示第j个变电单元由第i座220kV变电站供电。本文所用搜索算法流程如图3所示。
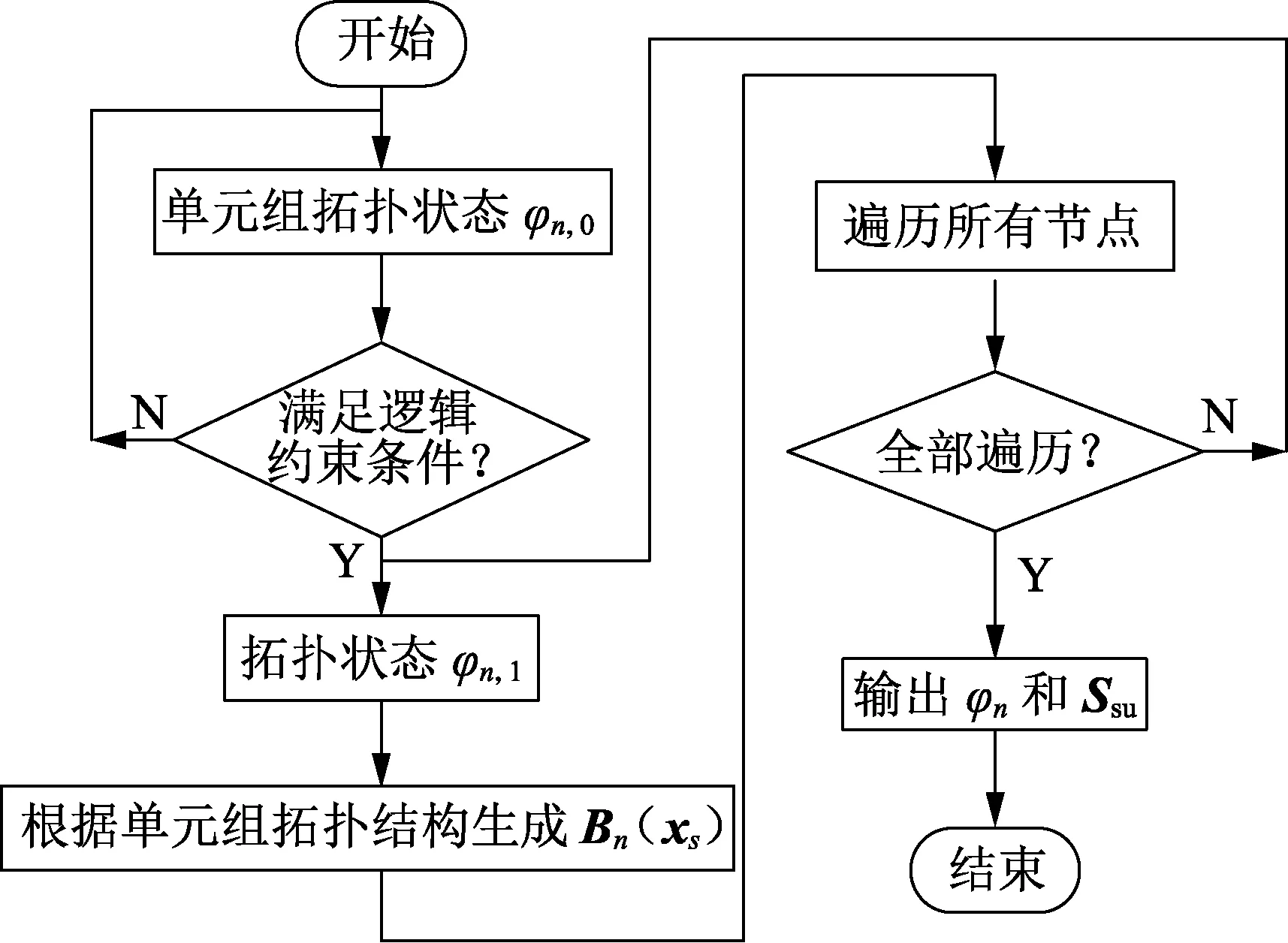
图3 可行拓扑状态搜索流程Fig.3 Flowchart of searching feasible topological state
根据矩阵Ssu,可得到φn中各拓扑状态下220kV变电站负载Tn(xs):
Tn(xs)=Ssu×Tn
(4)
其中,Tn为β×1维列向量,表示变电单元An的功率。
2 决策模型
本文采用机会约束规划,提出调整拓扑结构以均衡源荷功率分布的技术,理论上符合式(5)所描述的优化过程。
(5)
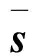
2.1 控制目标
针对中等规模风电非均匀接入的地区电网,本文通过功率均衡分布系数来衡量转供操作对局部消纳困难和局部负荷重载现象的优化效果,如式(6)、(7)所示。
f1=Exp(‖kq-kavg‖2)q=1,2,…,NT
(6)
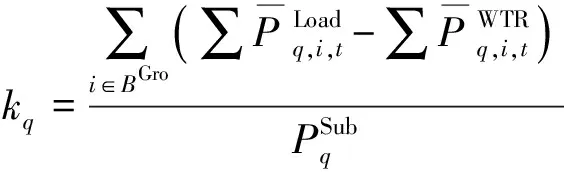
(7)
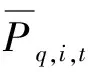
本文以功率均衡分布为目标,综合考虑断路器动作次数和可控DG功率调整,构建不确定性条件下110kV高压配电网的转供模型,见式(8)—(10)。

(8)
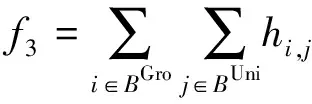
(9)
F=min(f1+a1f2+a2f3)
(10)
式(8)为转供操作过程中可操作断路器动作次数,xi,j为拓扑i下断路器j的状态,上标t,bef和t,aft分别表示t时刻优化前、后拓扑状态。式(9)为可控DG功率调整大小,即转供过程中调整局部地区可控DG功率以提高风电消纳能力、均衡负载,hi,j为变电单元组i内变电站j的可控DG功率调整大小。式(10)为本文所构建的综合目标函数,a1、a2为相应操作的惩罚系数。式(10)作为转供操作的目标函数,可保证断路器动作次数和可控DG功率调整在安全阈值内,使网络功率分布均衡,提高风电消纳能力、消除变电站重载。
2.2 约束条件
2.2.1 确定性约束条件
确定性约束条件主要有等式约束和不等式约束,见式(11)—(14)。
(11)

(12)
(13)

(14)
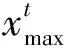
2.2.2 机会约束条件
系统机会约束包括节点电压约束、负载率约束和风电功率约束。由于风电功率和负荷功率的不确定性,无法定性描述确定性系统的状态约束,本文处理方法是希望系统状态约束以一定的置信水平α成立。其意义为:认为风电功率和负荷功率的预测值由于各种原因不够准确,不能追求系统状态约束的绝对满足,应在调度中考虑其不确定性,使系统状态约束大致满足。置信水平α用于衡量这种大致满足的程度和决策者对约束满足程度的期望,见式(15)—(18)。
(15)
(16)

(17)
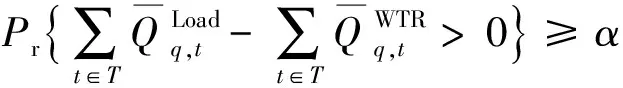
(18)
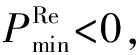
2.3 随机变量多状态模型

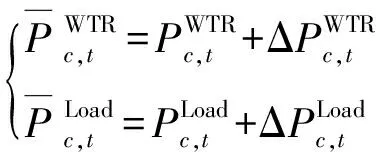
(19)
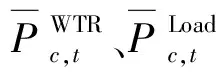
(20)
在此基础上,将f(ΔPc,t)离散化为7个区间,如图4所示,图中每个区间宽度为误差的标准差σ。
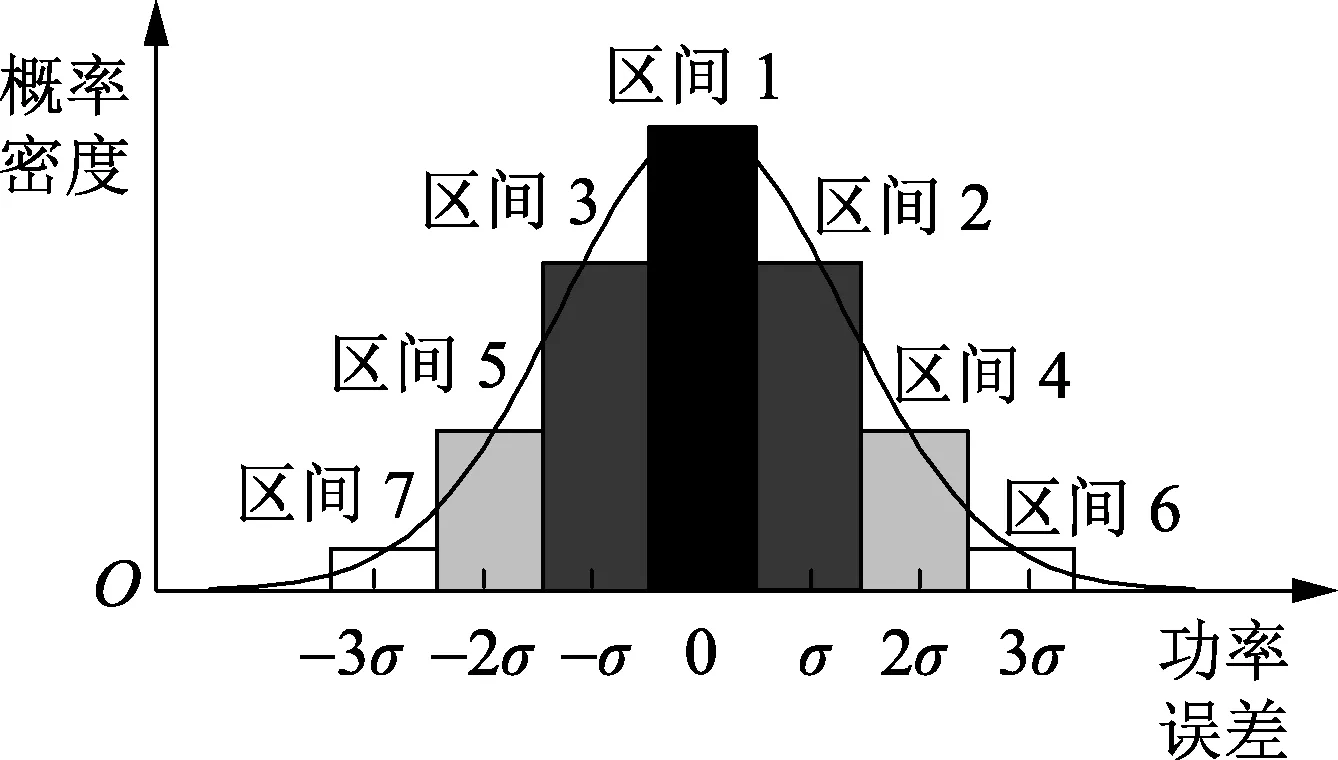
图4 功率误差概率密度函数离散化Fig.4 Discretization of power error PDF
将各区间概率标准化,如式(21)所示。
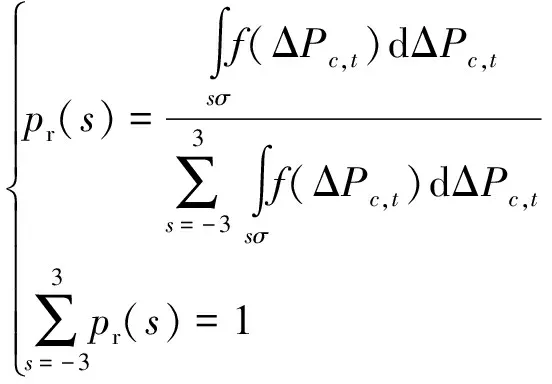
(21)
其中,pr(s)为区间概率;sσ为功率误差区间。
采用轮盘赌转生成0~1间的数得到其预测误差,即可依次确定各样本中随机变量的状态。
3 模型求解
3.1 十进制遗传算法
地区电网110kV配电网具有闭环设计、开环运行的特点,受辐射状拓扑结构和无“孤岛”约束。转供操作实则为断路器状态变化过程,如果采用二进制遗传算法对断路器状态进行0-1编码,搜索空间将会呈指数增大,使得求解效率降低[18]。因此本文所设计的变电单元组可行拓扑状态搜索算法,可预先保证网络拓扑的可行性。
故以变电单元组内可行拓扑状态为控制变量,同时为了规避二进制编码所带来的增加染色体长度及空解的问题,本文采用十进制遗传算法。以单元组内可行拓扑状态对基因编码,同时加入单元组可控DG功率调整大小h和切负荷量PENS,编码方案如式(22)所示。
(22)
根据式(6)—(10)计算种群各个体目标函数大小,并通过式(23)计算个体适应度。

(23)
其中,Nd为种群大小;d为根据目标函数大小所确定的个体在种群中的位置;Psp为选择压力,通常情况下1≤Psp≤2。
本文所采用十进制遗传算法的寻优范围为各单元组内可行拓扑状态的乘积,规模庞大,因此迭代过程中容易陷入早熟和局部最优。针对本文情况,动态地调整个体适应度ffit(d),即当种群进化代数y>K(K为规定常数)时,若检测到可能陷入局部最优,则调整最优个体适应度,见式(24)。
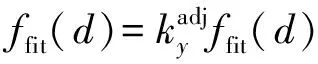
(24)

3.2 求解流程
首先由算法随机产生初始种群(式(22)),计算每一个体所对应目标函数(式(6)—(10)),并排序确定其适应度大小;根据适应度对种群进行遗传操作,并判断迭代过程中是否出现早熟情况并对其修改相应参数(式(24));最后,判断最优个体是否满足机会约会条件。算法流程见图5。
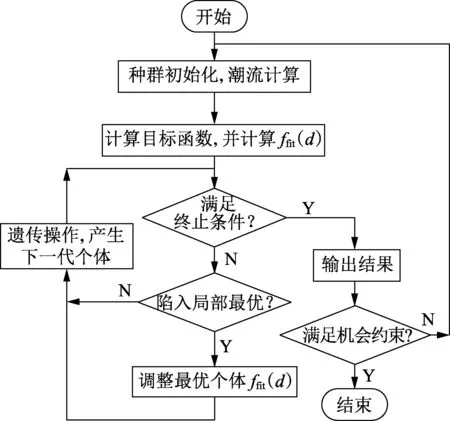
图5 十进制遗传算法流程图Fig.5 Flowchart of decimal genetic algorithm
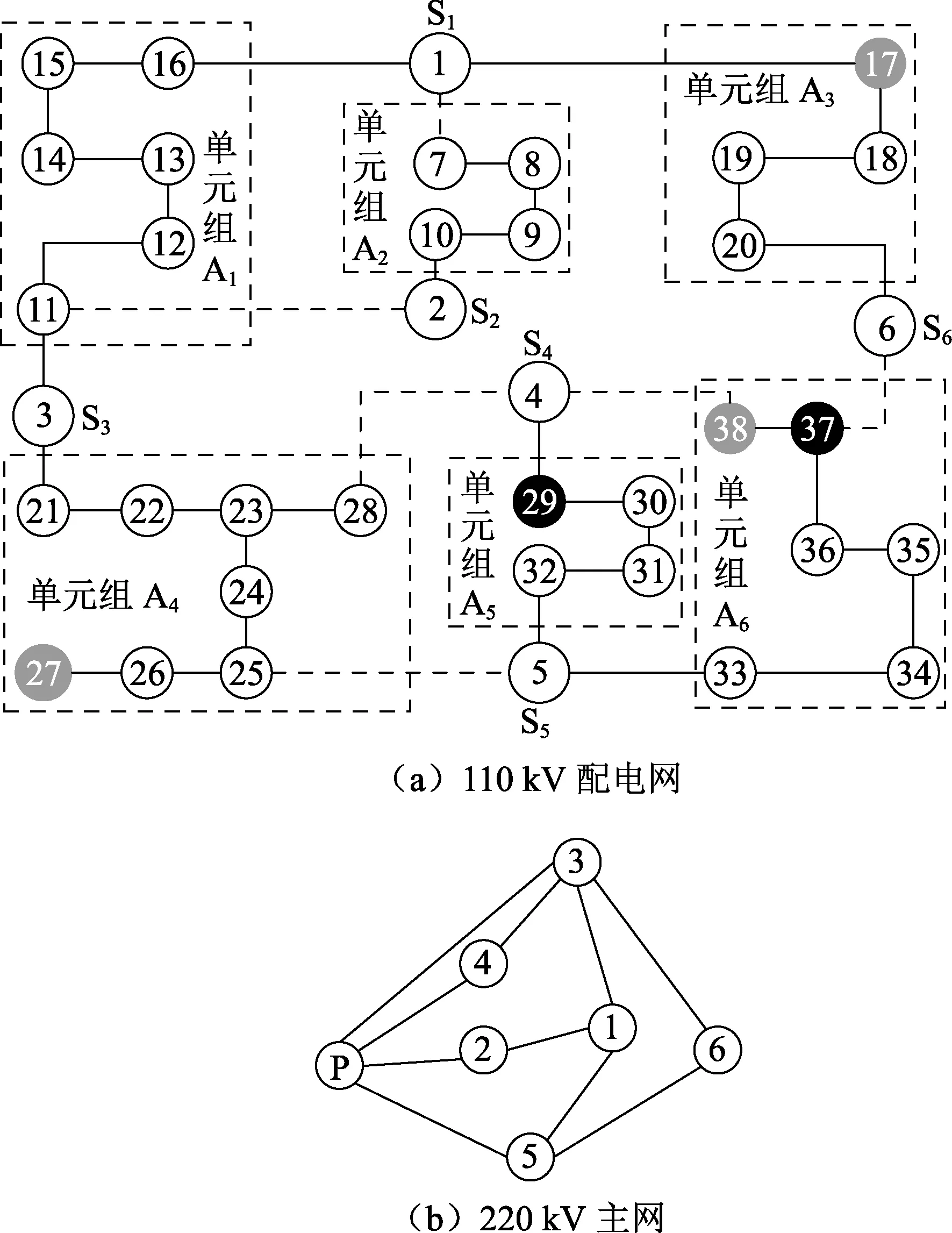
图6 地区高压电网局部系统Fig.6 Local regional high-voltage power system
4 算例仿真
以某地区电网局部系统验证所提模型的可行性和有效性,如图6所示。220kV系统共有6座变电站,10条线路;110kV系统共有32个变电单元,40条线路,其中9条线路处于备供状态,根据本文第1节所阐述的方法,将该系统分为6个变电单元组(A1—A6)。节点17处风电场的装机容量为150MW,节点27处风电场的装机容量为50MW,节点38处风电场的装机容量为100MW;节点29和节点37接有8MW的可控DG。
4.1 随机变量多状态表征
据气象部门通知,未来2h内有大风。由于各风电场地理的位置不同,故其确定性预测值差异较大;同时,考虑负荷的时序特性,单元组A3为重工业负荷,单元组A1、A4为轻工业负荷,单元组A2、A5和A6为商业及民用负荷;根据风电场历史统计数据可知,在特殊天气状况下风电场出力预测误差在不同时间点服从不同参数的正态分布,而各类型负荷波动较小,因此全时间点服从同一参数的正态分布。风电功率、负荷功率确定性预测值与其预测误差见表1(表中功率确定性预测值为标幺值)。表1中,ΔP为风电功率和负荷的预测误差,其服从标准差为σt的正态分布,具体计算见式(20)、(21)。
注:表头中数据为预测时间Tf。
4.2 优化转供后的系统运行状态
为了提高风电消纳能力、消除变电站重载现象,从Tf=0.5h开始采集负荷和风电数据,采用机会约束规划,取置信度α=0.9。根据系统运行状态进行转供操作,触发条件如下:
a. 220kV线路负载率上限和220kV变电站负载率上限为0.8时,式(16)不满足;
b. 式(17)不满足。
则未来2h内4个时间点220kV变电站负载率机会束条件与功率均衡分布系数f1见表2。

表2 220kV变电站负载率机会约束条件与f1Table 2 Load rate chance constraints of 220kV substation and f1
初始工况下(Tf=0.5h),220kV变电站S3带全部重工业负荷,负载率过高;而此时风速较大,节点38处风电场出力接近额定功率,无法就地消纳,变电站S6出现风电功率返送现象,此时Pr{0 图7 Tf=0.5h时转供前、后网络状况Fig.7 Network conditions before and after power transfer when Tf=0.5h Tf=1.0h时,风电功率和负荷功率未发生大幅度变化,Pr{0 图8 Tf=1.5h时转供前、后网络状况Fig.8 Network conditions before and after power transfer when Tf=1.5h Tf=1.5h时,风电功率各预测误差区间概率接近,此时220kV变电站负载率裕度不足以保证满足机会约束条件,触发转供操作,优化前、后的效果见图8。节点17处风电场出力减小造成变电站S6的负载率不满足机会约束条件,转供后变电站S6不再对单元组A3供电并接入节点38处风电场;变电站S4不接入风电后负载率提高,因此将部分负荷转供由给变电站S3和S5供电,并恢复节点27处可控DG出力3.12MW,确保变电站S4不出现过载现象。 Tf=2.0h时,节点17处风电场的功率进一步减小,变电站S1的负载率k1=0.7722,使其在机会约束条件下Pr{0 表3 断路器动作次数Table 3 Number of circuit breaker action 注:“A1中15-14断,11-2合”表示变电单元A1中线路15-14断路器断开,线路11-2断路器闭合;其他同。 图9 风电、负荷功率确定性预测值所占比例Fig.9 Proportion of wind power and load power deterministic predictive values 表3为对应时间转供操作断路器动作次数,图9为各时间风电功率和负荷功率确定性预测值所占比例。可以看出,在Tf=0.5h时,风电功率所占比例最大,此时转供主要是为了消除风电消纳困境,同时均衡重工业单元组内负荷分布。在Tf=1.5h时,风电功率降低造成部分变电站重载,此时转供主要是为了消除变电站重载现象、均衡负载。在Tf=2.0h时,风电功率进一步降低,上一时间网络重构后大部分变电站留有足够裕度,此时只针对局部地区进行小范围转供。 图10为转供前、后系统状态对比图。从图中可以看出,在Tf=0.5h时,风电消纳问题与变电站重载同时出现,f1=1.1809,系统功率分布极其不均衡;通过转供操作,将大量负荷转由风电消纳困难地区供电,提高风电消纳率的同时使得其余变电站有足够供电空间接纳重工业负荷,变电站负载量最大差值仅为13.64%。在Tf=1.5h时,风电功率下降导致之前因消纳风电而接入大量负荷的变量站负载率越限,转供后负载分布均衡,各变电站有足够供电空间使其满足机会约束式(16)。在Tf=2h时,最大负载率虽未越限,但此时风电功率误差区间概率接近致使越限风险较大,在置信度α=0.9下不满足约束,触发小范围转供操作。 图10 转供前、后系统状态对比Fig.10 Comparison of network condition before and after power transfer 表4 负荷削减量和弃风量Table 4 Load power reduction and wind power abandon 削减负荷和限制风电功率的方法虽然暂时性地消除了风电消纳和变电站重载问题,但系统处于不平衡运行状态,设备利用效率低。同时,考虑风电和负荷功率波动,为了保证各变电站不出现重载和功率返送风险(即满足机会约束条件),负荷削减量与弃风量均大于传统情况,使各变电站的裕度足够。 对比表2与表4可知,本文所提方法避免了切负荷和弃风现象的出现,利用高压配电网可转供的特点进行负荷疏导与风电消纳优化操作。 将本文模型与文献[19]中以断路器状态为控制变量的传统方法进行比较。基于机会约束规划,在MATLAB中采用遗传算法进行求解,在种群个数为50、迭代50次的情况下,不同规模网络规模Nu下的求解性能如表5所示。 表5 计算时间对比Table 5 Comparison of calculation time 由测试结果可知,本文所提模型在基于机会约束规划的求解过程中收敛性和计算时间上都优于传统模型,且随着网络规模的增大,效果越明显;当网络规模达到60时,传统模型在遗传算法迭代过程中不易收敛。这是因为以断路器状态编码的传统模型在迭代过程中会产生大量不满足拓扑约束的解不可行解,严重影响了迭代的收敛性。 中等规模风电经110kV/35kV系统直接并入地区高压电网已成为主流趋势,针对其非均匀接入而带来的消纳困难与负荷重载问题,本文提出基于高压电网灵活可转供的拓扑特点的机会约束转供模型。通过某地区实际算例得出,模型具有以下特点: a. 针对该地区网架结构灵活的特点,建立基于变电单元的高压配电网拓扑模型,考虑适用于模型特点的负荷转供逻辑约束条件,确定各单元组可行拓扑状态,提出了以此为控制对象的高压配电网转供模型,显著提高计算效率; b. 考虑风电、负荷功率的不确定性,以确定性预测值与预测误差之和的形式构建随机变量多状态模型,采用机会约束规划求解,使模型更加符合实际情况; c. 模型充分利用高压电网运行拓扑特点,均衡风电和负荷功率分布,避免了切负荷和弃风操作的出现,以提高设备利用率平抑运行风险。 本文所提方法对于风电非均匀接入后的高渗透率地区电网在运行过程中突发的消纳矛盾及运行阻塞有较强的疏导能力,同时提高了高压配电网的资产效率。另外,由于短时间内频繁的网络重构对配电网安全运行提出了挑战,因此针对110kV高压配电网特点,利用柔性直流互联装置对功率的解耦控制构建交直流混合配电网,实现更为高效的均衡负荷阻塞与新能源消纳矛盾策略亦是下一步的研究重点。 参考文献: [1] 刘文颖,文晶,谢昶,等. 基于源荷互动的含风电场电力系统多目标模糊优化调度方法[J]. 电力自动化设备,2014,34(10):56-63,68. LIU Wenying,WEN Jing,XIE Chang,et al. Multi-objective fuzzy optimal dispatch based on source-load interaction for power system with wind farm[J]. Electric Power Automation Equipment,2014,34(10):56-63,68. [2] 赵晋泉,唐洁,罗卫华,等. 一种含风电电力系统的日前发电计划和旋转备用决策模型[J]. 电力自动化设备,2014,34(5):21-27. ZHAO Jinquan,TANG Jie,LUO Weihua,et al. Day-ahead gene-ration scheduling and spinning reserve decision-making model for power grid containing wind power[J]. Electric Power Automation Equipment,2014,34(5):21-27. [3] 朱凌志,陈宁,韩华玲. 风电消纳关键问题及应对措施分析[J]. 电力系统自动化,2011,35(22):29-34. ZHU Lingzhi,CHEN Ning,HAN Hualing. Key problems and solutions of wind power accommodation[J]. Automation of Electric Power Systems,2011,35(22):29-34. [4] 刘畅,吴浩,高长征,等. 风电消纳能力分析方法的研究[J]. 电力系统保护与控制,2014,42(4):61-66. LIU Chang,WU Hao,GAO Changzheng,et al. Study on analysis method of accommodated capacity for wind power[J]. Power System Protection and Control,2014,42(4):61-66. [5] 王薪苹,卫志农,孙国强,等. 计及分布式电源和负荷不确定性的多目标配网重构[J]. 电力自动化设备,2016,36(6):116-121. WANG Xinping,WEI Zhinong,SUN Guoqiang,et al. Multi-objective distribution network reconfiguration considering uncertainties of distributed generation and load[J]. Electric Power Automation Equipment,2016,36(6):116-121. [6] 王林川,梁峰,李漫,等. 含有分布式电源配电网重构算法的研究[J]. 电力系统保护与控制,2011,39(5):41-44,50. WANG Linchuan,LIANG Feng,LI Man,et al. Research on the distribution network reconfiguration with the distributed generation[J]. Power System Protection and Control,2011,39(5):41-44,50. [7] 汲国强,吴文传,张伯明,等. 以降损和载荷均衡为目标的地区电网网络重构快速算法[J]. 电网技术,2012,36(11):172-178. JI Guoqiang,WU Wenchuan,ZHANG Boming,et al. Regional network reconfiguration algorithm for loss reduction and loading equilibrium[J]. Power System Technology,2012,36(11):172-178. [8] 余昆,曹一家,陈星莺,等. 含分布式电源的地区电网动态概率潮流计算[J]. 中国电机工程学报,2011,31(1):20-25. YU Kun,CAO Yijia,CHEN Xingying,et al. Dynamic probability power flow of district grid containing distributed generation[J]. Proceedings of the CSEE,2011,31(1):20-25. [9] 葛少云,郭明星,王成山,等. 城市高压配电网接线模式比较研究[J]. 电力自动化设备,2004,24(2):33-37. GE Shaoyun,GUO Mingxing,WANG Chengshan,et al. Comparative study of connection modes in high-voltage distribution networks[J]. Electric Power Automation Equipment,2004,24(2):33-37. [10] 金勇,刘友波,刘俊勇,等. 基于公共信息模型对象聚合的高压配电网功能单元信息模型[J]. 电力系统自动化,2016,40(9):106-112. JIN Yong,LIU Youbo,LIU Junyong,et al. CIM aggregation based functional units information model for high-voltage distribution network[J]. Automation of Electric Power Systems,2016,40(9):106-112. [11] 张曦,吕林,金勇,等. 基于高压配电网变电单元分组重构的城市电网输电阻塞管控模型及算法[J]. 中国电机工程学报,2016,36(20):5403-5413. ZHANG Xi,LÜ Lin,JIN Yong,et al. Congestion mitigation model and algorithm for urban power grids considering reconfigurability of high-voltage distribution transformer unit groups[J]. Proceedings of the CSEE,2016,36(20):5403-5413. [12] 江岳文,陈冲,温步瀛. 随机模拟粒子群算法在风电场无功补偿中的应用[J]. 中国电机工程学报,2008,28(13):47-52. JIANG Yuewen,CHEN Chong,WEN Buying. Application of stochastic simulation’s particle swarm algorithm in the compensation of reactive power for wind farms[J]. Proceedings of the CSEE,2008,28(13):47-52. [13] 王威,韩学山,李保银. 基于机会约束规划的含风机配电网重构[J]. 电力系统及其自动化学报,2014,26(5):23-26. WANG Wei,HAN Xueshan,LI Baoyin. Reconfiguration of distribution network with wind turbines based on chance-constrained programming[J]. Proceedings of the CSU-EPSA,2014,26(5):23-26. [14] 国家电网公司. 城市电力网规划设计导则:Q/GDW 156—2006[S]. 北京:中国电力出版社,2007. [15] LANGE M. On the uncertainty of wind power predictions-analysis of the forecast accuracy and statistical distribution of errors[J]. Journal of Solar Energy Engineering,2005,127(2):177-184. [16] DOHERTY R,MALLEY M O. A new approach to quantify reserve demand in systems with significant installed wind capacity[J]. IEEE Transactions on Power Systems,2005,20(2):587-595. [17] 刘健,徐精求,董海鹏. 配电网概率负荷分析及其应用[J]. 电网技术,2004,28(6):67-70,75. LIU Jian,XU Jingqiu,DONG Haipeng. Probabilistic load flow ana-lysis of distribution network and its application[J]. Power System Technology,2004,28(6):67-70,75. [18] 胡卫,黄纯,孙彦广,等. 基于人工培植杂交的配电网重构方法[J]. 电力自动化设备,2014,34(9):106-111. HU Wei,HUANG Chun,SUN Yanguang,et al. Distribution network reconfiguration based on artificial cultivated hybrid[J]. Electric Power Automation Equipment,2014,34(9):106-111 [19] ANDERVAZH M R,OLAMAEI J,HAGHIFAM M R. Adaptive multi-objective distribution network reconfiguration using multi-objective discrete particles swarm optimisation algorithm and graph theory[J]. IET Generation Transmission & Distribution,2013,7(12):1367-1382.


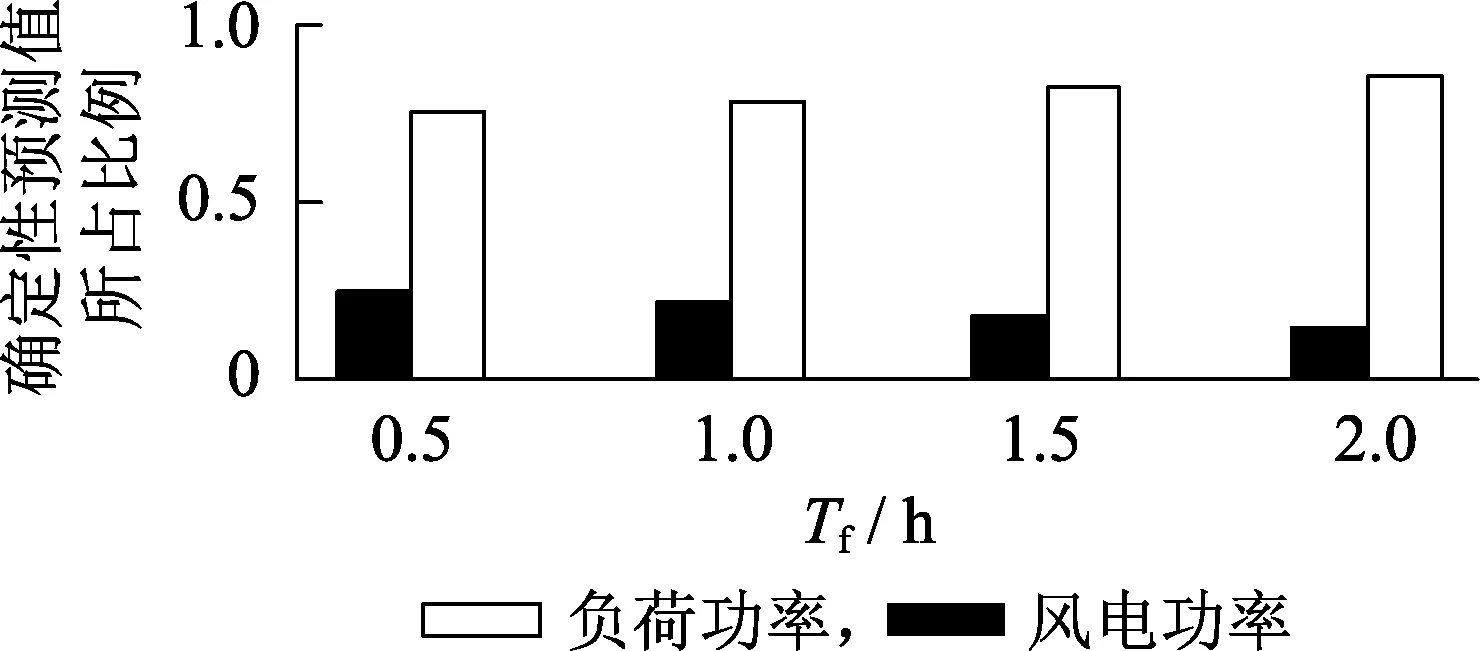

4.3 系统运行状态对比

4.4 计算效率对比

5 结论

