不同容量微网逆变器的自适应虚拟阻抗运行策略

王逸超，谢欣涛，陈仲伟，肖振锋，徐志强，陈耀红

(国网湖南省电力有限公司经济技术研究院，湖南 长沙 410004)

0 引言

随着微网规模的增大，不同容量等级的逆变器并联运行将成为发展趋势[1-3]。

当微网孤岛运行时，微网逆变器的输出功率按容量合理分配是逆变器并联运行的一个重要控制目标[4-7]。文献[2]提出一种功率分配的鲁棒下垂控制策略，通过人为构造积分环节实现有功功率的合理分配，但所提控制策略需要反馈公共连接点处的电压有效值，是一种有连线控制。虚拟阻抗法[8-10]通过在逆变器闭环控制外增加输出阻抗调节模块修正逆变器等效输出阻抗，通过在不同额定容量的逆变器间引入与容量成反比例的虚拟阻抗，可以近似实现总的线路阻抗与容量成反比。但考虑连线阻抗的存在，要满足线路阻抗与容量成反比，需增加较大的虚拟阻抗取值，这将对输出电压产生不利的影响。文献[11-12]提出一种自适应虚拟阻抗策略，使虚拟阻抗取值可以跟随逆变器的输出功率自动调节，获得了较好的功率分配效果，但并未将自适应虚拟阻抗策略与常规虚拟阻抗策略进行对比分析，且所提自适应虚拟阻抗策略是以额定容量的逆变器作为研究对象，如何扩展到不同容量的逆变器间应用需要进一步研究。

本文以阻性线路阻抗作为研究背景，提出适用于不同容量微网逆变器的自适应虚拟阻抗策略。通过与常规虚拟阻抗策略进行对比分析，理论证明在增加相同虚拟阻抗取值条件下，自适应虚拟阻抗策略可使逆变器等效线路阻抗更接近于容量的反比，从而提高功率分配效果。仿真和实验结果证明了本文所提不同容量微网逆变器并联运行策略的有效性。

1 线路阻抗差异对功率均分的影响

图1为微网运行结构图，其包含2台不同额定容量的微网逆变器。逆变器直流侧由储能装置维持稳定，逆变器输出通过LC滤波器滤除高频毛刺，再由线路连接到交流母线上。在低压微网系统中，连线阻抗以阻性为主。图中，z2、z2分别为逆变器1、2的连线阻抗；ZL为微网内负荷；微网逆变器1和微网逆变器2的容量分别为S1和S2。

图1 微网运行结构图Fig.1 Operation structure of microgrid

图2为图1对应的简化原理图。图中，U0°为公共连接点处母线电压；E1φ1和E2φ2为2台逆变器输出电压，φ1、φ2为2台逆变器的输出电压与母线电压的相角差；Z1θ1和Z2θ2为2台逆变器的等效线路阻抗，逆变器的等效线路阻抗包含逆变器输出阻抗与连线阻抗两部分。

图2 逆变器并联简化原理图Fig.2 Simplified schematic diagram of inverter in parallel connection

当等效线路阻抗以阻性为主时，θ1=θ2=0°，考虑到φi(i=1，2)一般很小，可近似认为sinφi=φi，cosφi=1，可得到逆变器i的输出有功功率和无功功率分别为：

(1)

(2)

其中，Zi(i=1，2)为逆变器i的等效线路阻抗。由此推导得到不同容量微网逆变器并联的反下垂控制表达式为：

ωi=ω*+miQi

(3)

Ei=E*-niPi

(4)

其中，ω*、E*分别为逆变器空载输出电压角频率和有效值；mi、ni为下垂控制系数；ωi和Ei分别为逆变器输出参考电压的角频率和有效值。此时逆变器参考电压信号可表示为：

(5)

2台逆变器最终稳定运行时，角频率会拉入同步，存在如下关系：

ω1=ω2

(6)

m1Q1=m2Q2

(7)

当频率无功下垂系数mi与逆变器容量成反比时，即可实现阻性线路阻抗条件下负荷的无功功率按逆变器容量比值精确分配。而对于有功功率的分配，将式(4)代入式(1)可得：

(8)

为了实现负荷有功功率按逆变器容量比合理分配，式(8)的分母项需与逆变器容量成反比。因此，电压有功下垂系数ni和逆变器的等效线路阻抗Zi均需要与逆变器的容量成反比，而实际中较难满足。因此阻性线路阻抗条件下，负荷的有功功率按逆变器容量比合理分配较难实现。

2 自适应虚拟阻抗策略

2.1 常规虚拟阻抗策略

采用虚拟阻抗策略可以在不增加系统损耗的前提下调整逆变器的输出阻抗。本文逆变器并联控制框图如图3所示。图中，L和C分别为滤波电感和滤波电容参数；kp、ki分别为电压外环比例谐振控制器的比例和积分系数；ke为电流内环P控制器比例系数；kPWM为逆变器增益；i0为逆变器入网电流；Eref为引入阻性虚拟阻抗后的参考电压信号；ZV为引入的虚拟阻抗。

图3 逆变器并联控制框图Fig.3 Parallel control of inverter

电压控制器采用比例谐振控制器可使逆变器自身等效输出阻抗幅值接近于0[5]，采用虚拟阻抗策略时，当引入的虚拟阻抗远大于逆变器自身等效输出阻抗时，虚拟阻抗将决定逆变器的输出阻抗大小。

电压有功下垂策略通过在式(8)的分母项引入与容量成反比例的niU，近似使分母项与逆变器的容量成反比。相类似地，常规虚拟阻抗策略通过引入与容量成反比例的虚拟阻抗，近似使式(8)分母项满足与逆变器容量成反比例的条件。2种策略改善有功功率分配的作用机理是相似的。

假设S1/S2=ns，逆变器1引入的虚拟阻抗为ZV0，则逆变器2引入的虚拟阻抗可表示为nsZV0，定义有功功率分配比为：

(9)

η越接近于1，表明有功功率的分配效果越好。将式(9)代入式(8)，并用逆变器虚拟阻抗和连线阻抗之和代替线路阻抗，可得：

(10)

下垂系数存在关系n2/n1=ns，分析式(10)可知，电压有功下垂系数n2和虚拟阻抗ZV0取值越大，有功功率分配比越接近1。

2.2 基于自适应虚拟阻抗的逆变器并联运行策略

为了简化控制，本文提出适用于不同容量微网逆变器的自适应虚拟阻抗运行策略。新的运行策略由频率无功下垂控制策略和自适应虚拟阻抗策略构成，省略电压有功下垂控制环节，逆变器输出电压有效值保持不变，控制框图如4所示。

图4 新型逆变器并联运行策略Fig.4 New parallel operation strategy of inverter

此时，有功功率分配比可改写成：

(11)

2台逆变器的虚拟阻抗表达式可表示如下：

ZV1=Z0+kP1

(12)

(13)

其中，Z0为虚拟阻抗的初始值；k为虚拟阻抗下垂系数；ns为2台逆变器的容量比。式(12)和式(13)实际上为虚拟阻抗与有功功率之间的下垂关系，通过有功功率反馈自适应地调节虚拟阻抗取值，使等效线路阻抗比朝接近逆变器容量反比的方向变化。

2.3 自适应虚拟阻抗策略与常规虚拟阻抗策略的对比分析

本节将通过反证法证明，在增加的虚拟阻抗取值相同的条件下，本文所提自适应虚拟阻抗策略相比常规虚拟阻抗策略，可以获得更好的功率分配效果。不妨假设连线阻抗存在关系：

z2>nsz1

(14)

常规虚拟阻抗策略下有功功率分配比可简化表示为：

(15)

采用自适应虚拟阻抗策略后，可得有功功率分配比为：

(16)

由反证法推导，假设：

(17)

可以得到：

(18)

若逆变器1采用自适应虚拟阻抗策略增加的虚拟阻抗取值与采用常规虚拟阻抗策略增加的虚拟阻抗取值相等，即：

ZV1=ZV0

(19)

nsZV1>ZV2

(20)

即有nsZV0>ZV2，从而可得到η1>η2>1。上述推导过程表明，在增加的虚拟阻抗取值接近的情况下，自适应虚拟阻抗策略相比常规虚拟阻抗策略能获得更好的功率分配表现。同理可以推导，在相同的功率分配效果条件下，自适应虚拟阻抗策略最终稳定时所需要的虚拟阻抗要比常规虚拟阻抗策略所需要的虚拟阻抗小，可以有效地减弱虚拟阻抗对输出电压精度的负面影响。

2.4 自适应虚拟阻抗策略对功率稳定性影响及下垂系数取值分析

采用自适应虚拟阻抗策略后，逆变器输出电压指令与输出有功功率之间存在非线性环节，逆变器输出有功功率的表达式为：

(21)

式(21)可展开为求解Pi的一元二次方程，如式(22)所示。

(22)

为了保证系统稳定运行，关于Pi的一元二次方程必须有解，并且还需存在恒大于0的正解，根据求根公式，有：

(23)

由于逆变器的虚拟阻抗大小随输出功率变化，为了使逆变器轻载时仍能获得可以接受的功率分配效果，推荐虚拟阻抗的初始值Z0应大于连线阻抗的1～3倍。为了避免虚拟阻抗选取过大影响公共连接点处的电压精度，可以推导得到k的最大取值近似为：

(24)

其中，Umin为公共连接点处允许的最低电压幅值；Pmax为逆变器允许的最大有功输出。

3 仿真及实验验证

为了验证上述理论的有效性，在MATLAB/Simu-link仿真平台搭建了两逆变器并联仿真模型。采用直流侧稳压源模拟分布式电源，逆变器1额定功率设为4 kW，逆变器2额定功率设为2 kW，逆变器容量比ns=2，带12 Ω阻性负载，载波频率设为10 kHz。仿真参数如下：滤波电感为2 mH，滤波电容为10 μF，逆变器1无功频率下垂系数为5×10-5，逆变器2无功频率下垂系数为1×10-4，电压有效值E*=235V，负载阻抗为12 Ω。逆变器1连线阻抗设定为0.3 Ω，逆变器2连线阻抗设定为0.1 Ω。

由于自适应虚拟阻抗策略增加的虚拟阻抗与逆变器输出功率密切相关，逆变器1虚拟阻抗初始值设置为0.6 Ω，使得2台逆变器在轻载时仍能获得可以接受的功率分配效果，自适应虚拟阻抗策略的下垂系数设置为2×10-4。

图5为逆变器2投入并联工作时的仿真结果，i2、i2分别为逆变器1和2连接线路上的电流，定义iH=i2-2i2，iH幅值越小，表明实际功率分配效果越好。从图5可见，逆变器2投入后，迅速与逆变器1分担负荷电流，iH幅值减小，证明自适应虚拟阻抗策略具有良好的环流抑制性能。

图5 2台逆变器输出电流Fig.5 Output currents of two inverters

为了验证在增加相同虚拟阻抗的条件下，自适应虚拟阻抗策略可使逆变器总的等效线路阻抗更接近于容量的反比，获得更好的功率分配表现。在1s前采用自适应虚拟阻抗策略，在1s后更换为常规固定虚拟阻抗策略，同时保持逆变器2的虚拟阻抗取值相同。

图6为2台逆变器在策略改变前后有功功率变化曲线和虚拟阻抗大小对比。从图6对比可见，在逆变器2虚拟阻抗取值相同的条件下，采用自适应虚拟阻抗策略时，逆变器1输出有功功率和逆变器2输出有功功率的2倍间的差距更小，有功功率分配比更接近1。因此，采用自适应虚拟阻抗策略在增加的虚拟阻抗接近的情况下，可使逆变器的等效线路阻抗更接近于容量的反比，获得更好的功率分配效果。

图6 有功功率和虚拟阻抗曲线Fig.6 Curves of active power and virtual impedance

图7(a)为策略改变前后的有功功率波形，2种策略的效果对比如表1所示。从图7(a)中可见，在逆变器2虚拟阻抗取值不变的条件下，采用自适应虚拟阻抗策略时，有功功率分配比更接近1，可以获得更好的功率分配效果。

图7(b)为采用自适应虚拟阻抗策略时2台逆变器稳态运行时的输出电流波形，图7(c)为2台逆变器稳态运行时的iH电流波形，可见，本文所提不同容量微网逆变器并联运行策略能够实现良好的功率分配效果。

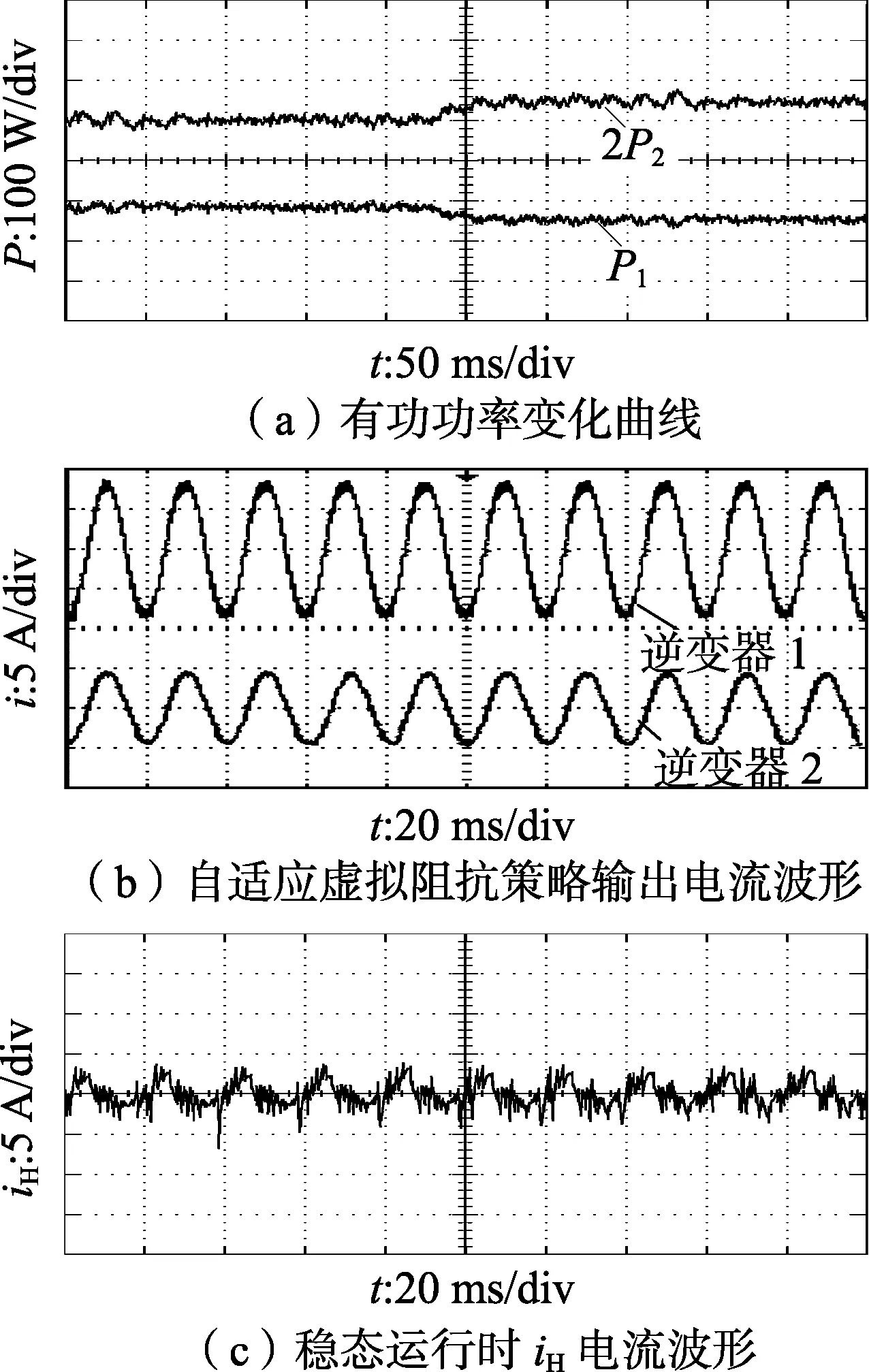
图7 实验波形Fig.7 Experimental waveforms

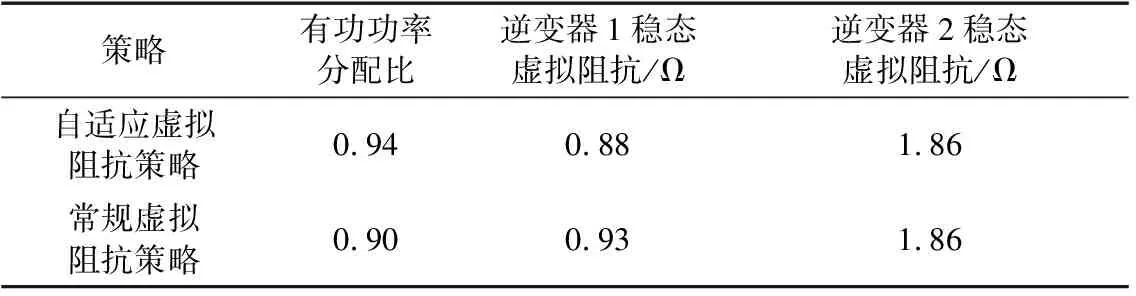
策略有功功率分配比逆变器1稳态虚拟阻抗/Ω逆变器2稳态虚拟阻抗/Ω自适应虚拟阻抗策略0.940.881.86常规虚拟阻抗策略0.900.931.86

4 结论

本文对不同容量微网逆变器的功率控制策略进行了研究，提出了适用于不同容量微网逆变器的自适应虚拟阻抗策略，通过理论和实验证明在增加相同虚拟阻抗的条件下，自适应虚拟阻抗策略可使逆变器总的线路阻抗更接近于容量的反比，从而提高功率分配效果。仿真和实验结果证明了本文所提不同容量微网逆变器并联运行策略的有效性。

参考文献：

[1] 吕志鹏，罗安. 不同容量微源逆变器并联功率鲁棒控制[J]. 中国电机工程学报，2012，32(12):35-42.

LÜ Zhipeng，LUO An. Robust power control of paralleled micro-source inverters with different power ratings[J]. Proceedings of the CSEE，2012，32(12)：35-42.

[2] QING Changzhong. Robust droop controller for accurate proportional load sharing among inverters operated in parallel[J]. IEEE Tran-sactions on Industrial Electronics，2013，60(4)：1281-1290.

[3] 吕志鹏，罗安，蒋雯倩，等. 多逆变器环境微网环流控制新方法[J]. 电工技术学报，2012，27(1):40-47.

LÜ Zhipeng，LUO An，JIANG Wenqian，et al. New circulation con-trol method for micro-grid with multi-inverter micro-sources[J]. Transactions of China Electrotechnical Society，2012，27(1)：40-47.

[4] 梁建钢，金新民，吴学智，等. 基于下垂控制的微电网变流器并网运行控制方法改进[J]. 电力自动化设备，2014，34(4)：59-64.

LIANG Jiangang，JIN Xinmin，WU Xuezhi，et al. Improved grid-connection operation of microgrid converter based on droop control[J]. Electric Power Automation Equipment，2014，34(4)：59-64.

[5] 关雅娟，邬伟扬，郭小强. 微电网中三相逆变器孤岛运行控制技术[J]. 中国电机工程学报，2011，31(33)：52-60.

GUAN Yajuan，WU Weiyang，GUO Xiaoqiang. Control strategy for three-phase inverters dominated microgrid in autonomous operation[J]. Proceedings of the CSEE，2011，31(33)：52-60.

[6] 彭春华，王立娜，李云丰. 低压微电网三相逆变器功率耦合下垂控制策略[J]. 电力自动化设备，2014，34(3)：28-33.

PENG Chunhua，WANG Lina，LI Yunfeng. Strategy of power-coup-ling droop control for three-phase inverter in low-voltage microgrid[J]. Electric Power Automation Equipment，2014，34(3)：28-33.

[7] 郑连清，庄琛，马世强，等. 微电网改进负荷功率分配策略与并网稳定性分析[J]. 电力自动化设备，2015，35(4)：17-23.

ZHENG Lianqing，ZHUANG Chen，MA Shiqiang，et al. Improved load power allocation strategy for microgrid and grid-connection stability analysis[J]. Electric Power Automation Equipment，2015，35(4)：17-23.

[8] 李金科，金新民，吴学智，等. 考虑数字控制影响的虚拟阻抗控制改进[J]. 电力自动化设备，2016，36(9)：134-141.

LI Jinke，JIN Xinmin，WU Xuezhi，et al. Improved virtual impe-dance control considering effect of digital control[J]. Electric Power Automation Equipment，2016，36(9)：134-141.

[9] YAO W，CHEN M，MATAS J，et al. Design and analysis of the droop control method for parallel inverters considering the impact of the complex impedance on the power sharing[J]. IEEE Transactions on Industrial Electronics，2011，58(2)：576-588.

[10] GREGOIRE J M，LOBOVSKY M B，HEINZ M F，et al. Decentra-lized control for parallel operation of distributed generation inverters using resistive output impedance[J]. IEEE Transactions on Industrial Electronics，2007，54(2):994-1004.

[11] GUERRERO J M，LUIS G D V，JOSÉ M，et al. Output impedance design of parallel-connected UPS inverters with wireless load-sharing control[J]. IEEE Transactions on Industrial Electronics，2005，52(4)：1126-1135.

[12] GUERRERO J M，MATAS J，LUIS G D V，et al. Wireless-control strategy for parallel operation of distributed-generation inverters[J]. IEEE Transactions on Industrial Electronics，2006，53(5)：1461-1470.